【学习笔记】网络流
Echoternity
·
2022-11-18 18:02:58
·
个人记录
"或有一次天命陨落,但层出不穷,使万物若然。"
网络
网络流是网络中的流,网络是一张有向图,表示为 G=(V,E) ,对于每一条边 (u,v) ,存在一个权值 c(u,v) 表示容量 (capacity) ,当 (u,v)\notin E ,则有 c(u,v)=0 ,注意,不保证 c(u,v)=c(v,u) 。每一个网络有两个特殊点,一个是源点 (Source) s\in V ,一个是汇点(Sink) t\in V,(s\neq t) 。
流
一个实数函数满足 f(u,v),(u\in V,v\in E) ,且有:
容量限制 f(u,v)\leq c(u,v) ;
流守恒性 \sum^{i\in V,i\neq s}_{i}f(s,i)=\sum^{j\in V,j\neq t}_{j}f(j,t) ,即从源点流出的流量等于汇点流入的流量。
如果考虑反向边,则有第三性质:斜对称性 f(u,v)=-f(v,u) 。f 是 G 的流函数, f(u,v) 被称为 (u,v)\in E 的流量,而 f’(u,v)=c(u,v)-f(u,v) 称为边的剩余流量。则 \sum_{(s,v)\in E}f(s,v) 为从源点出发的流量和。
最大流
可以把网络流看作水库出水,而源点则是水库,汇点就是你家。源点的“量”是无限的,中途的任何一个点不存储任意一点流量也不会产生任何一点流量,所以源点出发的所有流量必定流入汇点。而经过每一条边的最大流量,即是 c(x,y)
最大流的算法,就是在满足流过边 c 的流量满足 \leq c(x,y) 的情况下,汇点的流量最大的问题。
残余网络
首先我们介绍一下一条边的剩余容量 c_f(u,v) (Residual Capacity),它表示的是这条边的容量与流量之差,即 c_f(u,v)=c(u,v)-f(u,v) 。
对于流函数 f ,残量网络 G_f (Residual Network)是网络 G 中所有结点 和剩余容量大于 0 的边构成的子图。形式化的定义,即 G_f=(V_f=V,E_f=\{(u,v)\in E,c_f(u,v)>0\}) 。
注意,剩余容量大于 0 的边可能不在原图 G 中(根据容量、剩余容量的定义以及流函数的斜对称性得到)。可以理解为,残量网络中包括了那些还剩了流量空间的边构成的图,也包括虚边(即反向边)。
以下是二月份初学时做下的笔记。
我们设 f(x,y) 为边 (x,y) 的实际容量。
饱和弧: f(x,y)=c(x,y) ,流量为该边的容量
非饱和弧: f(x,y)<c(x,y) ,实际流量小于容量
零流弧: f(x,y)=0 ,该边未流过流量。
非零流弧: f(x,y)>0 ,当前流量不为 0 。
残余网络:设有容量网络 G(V,E) 及其上的网络流 f , G 关于 f 的残留网络即为 G(V’,E’) ,其中 G’ 的顶点集 V’ 和 G 的顶点集 V 相同,即 V’=V ,对于 G 中任何一条弧 (u,v) ,如果 f(u,v)<c(u,v) ,那么在 G’ 中有一条弧 (u,v)\in E’ ,其容量为 c’(u,v)=c(u,v)-f(u,v) ,如果 f(u,v)>0 ,则在 G’ 中有一条弧 (v,u)\in E’ ,其容量为 c’(v,u)=f(u,v) 。
从残留网络的定义来看,原容量网络中的每条弧在残留网络中都化为一条或者两条弧。在残留网络中,从源点到汇点的任意一条简单路径都对应一条增光路,路径上每条弧容量的最小值即为能够一次增广的最大流量。
增广路
增广路是一条从源点到汇点的路径,满足所有边的剩余容量都大于 0 ,则该路是网络 G 的一条增广路(Augmenting Path)。也可以定义为:残余网络 G_f 中,存在一条从源点到汇点的路径被称为增广路。
以下是二月份自学时做的笔记。
增广路是一条链。(链是网络中的一个顶点序列,这个序列中前后两个顶点有弧相连)链上的前向弧都是非饱和弧,链上的后向弧都是非零弧。(前向弧即输入的边,后向弧即建立的反边)链的起点是源点,终点是汇点。
增广路是一个边的集合,从 S 至 T 的一条路径。增广路的最大流量表示该路径经过的边中流量最小的边的流量,即:
一条增广路 i 的边集是 E_i ,最大流量是 c ,则 \forall r\in E,c_r\leq c 。
用赵悦岑巨佬的话来讲,增广路指的就是一条从源点到汇点,且经过的边最小容量不为 0 的路径。而我们寻找增广路之后,就会将所有经过的边的容量减去增广路的流量。但是,这种算法并不保险。所以我们对于每一条存在的 c(x,y) ,都建立其后向弧满足 c(y,x)=0 使得我们在后续寻找增广路时可以“反悔”,使其不因之前的错误增广路而影响。
我们对于每一条边都增加一条容量为 0 反向边,找到增广路后经过的边流量要减去此增广路的流量,其反向边的流量还要加上此增广路的流量。所有反向边组成的图就是残留网络。
反向边
增广时需要建造反向边,这是通理,虽然我也没有想明白其正确性。总之,增广的时候,由于贪心原则,其并非全局最优解,而减去之后会导致最优解无法到达,我们要让子程序进行反悔。那么,我们每次增广的时候,就要建造一个反向边满足 c(v,u)=f(u,v) ,即反向边的容量是正向边的流量。我无法解释为什么,反正它确实对了。
对于建反向边的技巧,邻接矩阵就是 table[x,y]=table[y,x] 。而链式前向星更常用,我们也不需要在增广时才加入反向边,我们可以预处理出反向边,而在用的时候直接将 id\operatorname{xor}1 即可。这个不必太多解释。但是,初始值需要有 Total=-1 或者 Total=1 ,如果边从 1 开始,则会错位。
Edmonds-Karp 动能算法
圈内人称 \text{EK} 算法。
算法只有一句话,用 \text{bfs} 找增广路,然后对其进行增广即可。
找:从源点开始 \text{bfs} ,直到碰到汇点,然后进行增广(每一条路),注意流量合法。
增广:重走找到的增广路,然后减去这条路能够达到的最大流量,然后把答案加上最小流量即可。时间复杂度 \mathcal O(nm^2) ,不太效率。但是好想和好记。
时间复杂度 \mathcal O(nm^2) ,不太效率,但是比较好想也比较好记。
const int MAXN=201,MAXM=5001;
const int INF=0x7f7f7f7f;
namespace EdmondsKarp
{
int Total;
vector<Edge>Edges;
vector<int>G[MAXN];
int fl[MAXN],id[MAXN];
inline void init()
{
for(int i=1;i<=N;++i) G[i].clear();
Edges.clear();
}
inline void addEdge(int u,int v,int c)
{
Edges.push_back(Edge(u,v,c,0));
Edges.push_back(Edge(v,u,0,0));
Total=Edges.size();
G[u].push_back(Total-2);
G[v].push_back(Total-1);
}
inline ll maxFlow(int s,int t)
{
ll flow=0;
for(;;)
{
memset(fl,0,sizeof(fl));
queue<int>Q;
Q.push(s);
fl[s]=INF;
while(!Q.empty())
{
int u=Q.front();Q.pop();
for(int i=0;i<G[u].size();++i)
{
Edge& e=Edges[G[u][i]];
if(!fl[e.to]&&e.cap>e.flow)
{
id[e.to]=G[u][i];
fl[e.to]=min(fl[u],e.cap-e.flow);
Q.push(e.to);
}
}
if(fl[t]) break;
}
if(!fl[t]) break;
for(int u=t;u!=s;u=Edges[id[u]].from)
{
Edges[id[u]].flow+=fl[t];
Edges[id[u]^1].flow-=fl[t];
}
flow+=fl[t];
}
return flow;
}
};
using namespace EdmondsKarp;
int main()
{
// freopen("ek.in","r",stdin);
// freopen("ek.out","w",stdout);
read(N,M,S,T);
EdmondsKarp::init();
for(int i=1,u,v,c;i<=M;++i)
{
read(u,v,c);
EdmondsKarp::addEdge(u,v,c);
}
printf("%lld",EdmondsKarp::maxFlow(S,T));
return 0;
}Dinic
在学习完 \text{EK} 之后,我才真正开始理解 \text{Dinic} 的本质。
思路同 \text{EK} ,但是在增广之前,使用 bfs 进行分层(将图进行分层处理,建图的常见技巧之一),源点的层数满足 dep[s]=0 ,其他点的层数取决于其与源点的距离。
分层之后,有两个优化:
同时进行多路增广,且在断层时(即找不到增广路的时候)直接中断增广,进行时间优化;增广路一定最短。我们用 dfs 来找增广路。对层数加 1 的点进行增广(从而确保增广路最短,原理同最短路,因为同层的点只会经过一个)。
Dinic 的优化
多路增广:每找到一条增广路之后,从残余流量再次增广;从而在一次 dfs 中找出多条增广路,提高算法效率。
当前弧优化:可以推出(或者直接背下),一条边如果已经是一条增广路的边(被增广过),那么这条边不可能被增广第二次。所以,对所有边进行标记,不必要再走已经被增广过的边。
在运用了上述两个优化之后,时间复杂度可以达到 \mathcal O(n^2m) ,在稠密图上比 EK 更胜一筹。就和 SPFA 一样,这个上界一般而言很难到达,且在二分图最大匹配问题上,Dinic 算法的复杂度能达到 \mathcal O(m\sqrt n) ,不过不在我今天讲的范围内,所以只是提一嘴。
以下讲解不太明晰(个人意见),酌情观看。
每次多路增广: u 点通过一条边,向 v 输出流量以后, v 会尝试到达汇点(到达汇点才真正增广),然后 v 返回实际增广量。这时,如果 u 还有没用完的供给,就继续尝试输出到其它边。
但是要警惕绕远路、甚至绕回的情况,不加管制的话极易发生。怎么管?
源点顺着残量网络想要到达其它点,需要经过一些边对吧?按照经过的边数(即源点出发以后的距离)把图分层,即用 bfs 分层。 每次尝试给予时,只考虑给予自己下一层的点,就可以防止混乱。
综合上面两条。每回合也是从源点出发,先按照当前残量网络分一次层,随后多路增广,尽可能增加流量。增广过程中,会加入一些反向边,这些反向边逆着层次图,本回合并不会走。所以还需要进入下一回合。一直到 bfs 分层时搜不到汇点(即残量网络断了)为止。
##### Dinic 的当前弧优化
$dfs$ 过程中我们会一直流直到把一条边流完再转到下一条边,如果一条边有容量但是却没有增广路,说明这条边的下一个点已经没有更多容量了,我们就可以把连接的这个点的高度标记为 $0$ ,下一次就不会再搜索到这个点了。
不过 $Dinic$ 还是很慢,甚至比 $EK$ 还慢,这时候我们就需要拯救 $Dinic$ 的当前弧优化。上面说到, $dfs$ 过程中会一直流直到把一条边流完再转到下一条边,当搜索到一条边的时候说明这条边之前的所有边都已经没有增广路了,我们就可以直接将 $t$ 指向这条边,这样下一次就不会再次搜索已经没有流量的边了。
### MPM
有两种实现方法,一种是基于堆的优先队列,时间复杂度 $\mathcal O(n^3\log n)$ ;一种是使用 $bfs$ 的解法,时间复杂度 $\mathcal O(n^3)$ 。其中寻找增广路的时间用了 $\mathcal O(n^2)$ ,而在寻找的过程中,考虑顶点而非边的容量。
在分层网络 $L$ 中引入定义点的函数 $p[v]$ 表示点 $v$ 传入残量和传出残量的最小值,满足:
$$
p_{in}(v)=\sum_{(u,v)\in L}(c(u,v)-f(u,v))
$$
$$
p_{out}(v)=\sum_{(v,u)\in L}(c(v,u)-f(v,u))
$$
$$
p(v)=\min(p_{in}(v),p_{out}(v))
$$
$r$ 为参考节点当且仅当 $p(r)=\min p(v)$ 。这是 MPM 特有的定义。
对于 $\text{MPM}$ 的其他内容,读者可以自行查阅。~~也没什么太大必要学(不要刀我)~~,更重要的是 $\text{Dinic}$。
~~主要是懒得写了~~。
---
### ISAP
与 $\text{Dinic}$ 不同的是,我们跑反图,即从 $t$ 向 $s$ 推进。增广的时候,选择比当前点层数少 $1$ 的点来增广。每一次也不需要重跑 $bfs$ 来重新分层,而是一边增广,一边重分层。
其实吧,$\text{SAP}$($\text{Shortest Augument Path}$,最短增广路)就是 $\text{EK}$ 算法。
在结束对 $i$ 点增广之后,我们遍历残量网络中 $i$ 的出边,找出其层最小的出点 $j$ ,令 $d_i=d_j+1$ ,若 $i$ 无出边,则有 $d_i=n$ 。如果 $d_s\ge n$ 则图不存在增广路。
#### ISAP 的当前弧优化 x ISAP 的 GAP 优化
当前弧优化不必多说。
记录层数为 $i$ 的点的数量,并在更新层数时更新 $num$ 数组,如果存在 $num_x=0$ ,则图断层,不存在增广路,将 $d_s=n$ ,终止算法。该优化称为 GAP 优化。
加上两个优化的 $ISAP$ 基本上可以吊打除了 $HLPP$ 以外的所有算法。
``` c++
int N,M,S,T;
struct Graph
{
int next,to;
ll val;
Graph(int n=0,int t=0,ll v=0):next(n),to(t),val(v){}
}Edge[MAXM<<1];
int Head[MAXN],Cur[MAXN],Total=1;
inline void addEdge(int u,int v,ll w)
{
Edge[++Total]=Graph(Head[u],v,w);Head[u]=Total;
Edge[++Total]=Graph(Head[v],u,0);Head[v]=Total;
}
int Dep[MAXN],Num[MAXN];
inline void Bfs()
{
memset(Dep,-1,sizeof(Dep));
memset(Num,0,sizeof(Num));
Dep[T]=0;Num[0]=1;
queue<int>Q;
Q.push(T);
while(!Q.empty())
{
int u=Q.front();Q.pop();
for(int e=Head[u];e;e=Edge[e].next)
{
int v=Edge[e].to;
if(Dep[v]!=-1) continue;
Q.push(v);
Dep[v]=Dep[u]+1;
++Num[Dep[v]];
}
}
return ;
}
ll MaxFlow;
ll Dfs(int u,ll inf)
{
if(u==T)
{
MaxFlow+=inf;
return inf;
}
ll flow=0;
for(int e=Cur[u];e;e=Edge[e].next)
{
Cur[u]=e;
int v=Edge[e].to;
if(Edge[e].val&&Dep[v]+1==Dep[u])
{
ll k=Dfs(v,min(Edge[e].val,inf-flow));
if(k)
{
Edge[e].val-=k;
Edge[e^1].val+=k;
flow+=k;
}
if(flow==inf) return flow;
}
}
--Num[Dep[u]];
if(Num[Dep[u]]==0) Dep[S]=N+1;
++Dep[u];
++Num[Dep[u]];
return flow;
}
inline ll ISAP()
{
MaxFlow=0;
Bfs();
while(Dep[S]<N)
{
memcpy(Cur,Head,sizeof(Head));
Dfs(S,INF);
}
return MaxFlow;
}
int main()
{
// freopen("isap.in","r",stdin);
// freopen("isap.out","w",stdout);
read(N,M,S,T);
for(int i=1,u,v;i<=M;++i)
{
ll w;
read(u,v,w);
addEdge(u,v,w);
}
printf("%lld",ISAP());
return 0;
}
```
---
### 预流推进
我们可以稍微回想一下网络流的形象化定义:
> 可以把网络流看作水库出水,而源点则是水库,汇点就是你家。源点的“量”是无限的,中途的任何一个点不存储任意一点流量也不会产生任何一点流量,所以源点出发的所有流量必定流入汇点。
那么,我们在处理网络流的时候,也可以看做不停从源点倒水,然后能流就流直到流完为止,最后看汇点有多少流量。~~听着就跟个大模拟一样。~~
这就是所谓**预流推进**的本质:
在求解过程中忽略流守恒性,并每次对一个节点更新消息,以求解最大流。
但是,如果真去模拟的话,你会发现最后的时间复杂度甚至没有过不了网络最大流模板题,更不要说预流推进的模板题了。这就要引出最大流的最后一个算法:
最高标号预流推进算法($\text{Highest\ Label\ Preflow\ Push}$)。
### HLPP
其实还有一个通用的预流推进算法(称为 $\text{Push-Relabel}$ ),但考虑在预流推进这个东西本来就冷门,我也不想学了。
> 网络流,网络流,学到秃头。
引出一些定义:
#### 流函数
同样是 $f$ 函数,但是不一定保持流守恒性;在预流推进里,我们允许入流大于出流。并将超过的那部分称为 $u(u\in V-\{S,T\})$ 结点的超额流,记作 $e(u)$ ,满足:
$$
e(u)=\sum_{(x,u)\in E}f(x,u)-\sum_{(u,y)\in E}f(u,y)
$$
若 $e(u)>0$ ,则称为 $u$ 溢出,当然,溢出结点不会包括源点和汇点。
#### 高度函数
预流推进维护每个结点的高度 $h(u)$ ,并规定溢出的结点 $u$ 如果要推送超额流,只能向满足 $h(u)>h(v)$ 的 $v$ 结点推送;如果 $u$ 没有相邻的高度小于 $u$ 的结点,就修改 $u$ 的高度,称为重贴标签。
实际上,预流推进维护一个映射 $h:V\to \mathbf N$ :
* $h(s)=|V|,h(t)=0$ ;
* $\forall (u,v)\in E,h(u)\le h(v)+1$ 。
则 $h$ 函数是残量网络 $G_f=(V_f,E_f)$ 的高度函数。有性质:
> 设 $G_f$ 中的高度函数为 $h$ ,则如果有 $\forall u,v\in V,h(u)>h(v)+1$ ,则 $(u,v)$ 不是 $G_f$ 的边。
预流推进只会在满足 $h(u)=h(v)+1$ 的边执行推送。
#### 推送(Push)
在 $u$ 溢出时,且存在 $v$ 满足 $(u,v)\in E_f,c(u,v)-f(u,v)>0,h(u)=h(v)+1$ 时执行。
将 $u$ 的超额流从 $u$ 推送到 $v$ 去,只考虑超额流和 $c(u,v)-f(u,v)$ 的最小值,无需考虑 $v$ 的溢出情况。
如果 $(u,v)$ 在推送完之后满流,则将 $(u,v)$ 从残量网络中删除。
#### 重贴标签(Relabel)
在 $u$ 溢出时,且任意 $v$ 满足 $\forall (u,v)\in E_f,h(u)\le h(v)$ 时执行。
执行时,将 $h(u)$ 更新为 $\min_{(u,v)\in E_f}h(v)+1$ 即可。
#### 初始化
初始化流函数,超额流函数和高度函数:
$$
\begin{aligned}
&\forall (u,v)\in E,f(u,v)=
\begin{cases}
c(u,v)&,u=s
\\
0&,u\ne s
\end{cases}
\\
&\forall u\in V,h(u)=
\begin{cases}
|V|&,u=s
\\
0&,u\ne s
\end{cases}
\\
&\forall u\in V,e(u)=\sum_{(x,u)\in E}f(x,u)-\sum_{(u,y)\in E}f(u,y)
\end{aligned}
$$
这样的初始化使 $(s,u)\in E$ 都可以满流,并使 $h(s)$ 抬高,满足 $(s,u)\notin E_f$ 。
因为 $h(s)>h(v)$ ,且 $(s,v)$ 满流,则 $(s,v)$ 没有必要留在残量网络中;
上述操作还将 $e(s)$ 初始化为 $\sum_{(s,v)\in E}f(s,v)$ 的相反数。
#### HLPP 的实质
有一个不为人知,但众所皆知的网络流算法——$\text{PP}$ 算法,是唯一一个会在模板题上超时的算法。它就是推进算法,用一个队列储存待维护的点(起始为源点),然后对于每一个当前点,把它有的流量尽可能地推往与之相连的点,然后将相连的点也加入队列。
但是,如果存在两个点可以互相推送,则会死循环。这也是为什么 $\text{PP}$ 是一个不成功的算法。所以才会出现 $\text{HLPP}$ ,类似于 $\text{Dinic}$ 构建一个高度函数 $h_i$ 。
著名毒瘤科学家 $\text{Tarjan}$ 和他的同事 $\text{Goldberg}$ 在 $1986$ 年提出了最高标号预留推进算法,将 $\text{PP}$ 中的队列替换为优先队列,每一次都流高度最高的,可以理解为先将高处的点的水移到低处,那么给低处节点推流时可以顺便带走。后来,另外两名科学家 $\text{Cheriyan}$ 和 $\text{Maheshwari}$ 证明了 $\text{HLPP}$ 的复杂度:
$\mathcal O(n^2\sqrt m)$ 。
每一次扫描整个图,只要存在结点 $u$ 能够执行 push 或 relabel 操作,就执行。下图是暴力推进的示意图:颜色深度代表结点高度,绿色边代表满足 $h_u=h_v+1$ 的边 $(u,v)$ 。
结果:
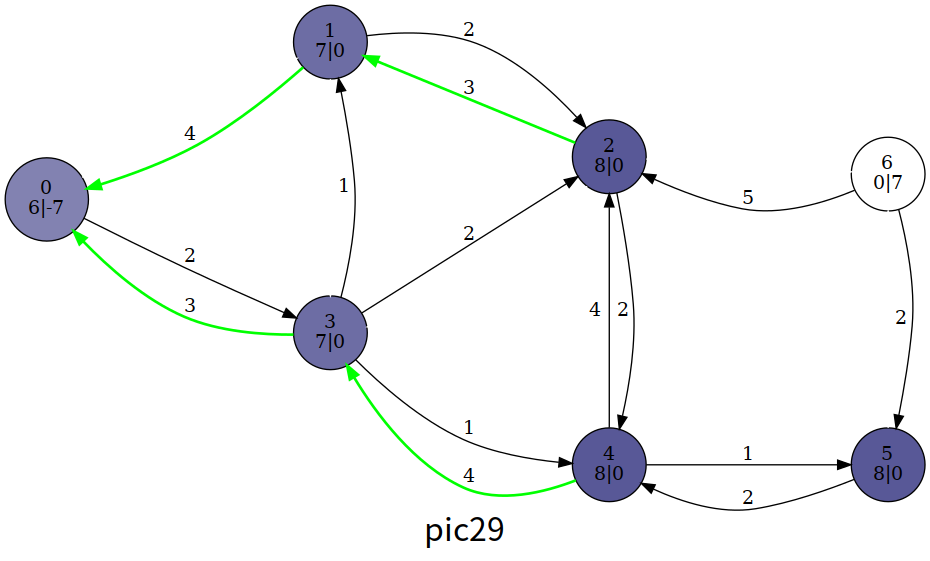
图片来自 $\text{OI-Wiki}$ 。
#### HLPP 的实现及优化
$\text{HLPP}$ 的算法过程包括:
1. 初始化(基于预流推进);
2. 选出溢出结点中高度最高的结点 $u$ ,推送 $u$ ;
3. 如果 $u$ 仍然溢出,重贴标签 $u$ ,并执行步骤 $2$ ;
4. 没有溢出,算法结束。
所涉及的三个操作上文都有讲过,读者请自行查阅。
$\text{HLPP}$ 的复杂度是较稳定的 $\mathcal O(n^2\sqrt m)$ ,卡得比较紧,且常数极大。在随机数据上甚至可能连 $\text{Dinic}$ 都跑不过,所以需要许许多多的优化。
##### BFS 优化
优化初始化高度,将 $h_u$ 赋为 $u$ 到 $T$ 的最短距离,使 $h_S=|V|$ 。并在使用 $\text{BFS}$ 时检查图的连通性,排除无解的情况。
##### GAP 优化
如果在某一刻存在 $h_u=T$ 的结点个数为 $0$ ,则对于 $h_u>T$ 的结点就永远无法推送超额流到 $T$ ,只能流回 $S$ 。所以直接改变高度到至少 $|V|+1$ ,以尽快推送回源点,减少重贴标签操作的复杂度。
#### 代码实现
``` c++
const int MAXN=1e3+2e2+1,MAXM=1e5+2e4+1;
const int INF=0x3f3f3f3f;
int N,M,S,T;
struct Net
{
int next,to,val;
Net(int n=0,int t=0,int v=0):
next(n),to(t),val(v){}
}Edge[MAXM<<1];
int Head[MAXN],Cur[MAXN],Total=1;
inline void addEdge(int u,int v,int w)
{
Edge[++Total]=Net(Head[u],v,w);Head[u]=Total;
Edge[++Total]=Net(Head[v],u,0);Head[v]=Total;
}
int Ht[MAXN+1],Ex[MAXN+1],Gap[MAXN+1];
stack<int>B[MAXN];
int Level=0;
inline int Push(int x)
{
bool Init=x==S;
for(int e=Head[x];e;e=Edge[e].next)
{
const int &v=Edge[e].to,&w=Edge[e].val;
if(!w||(!Init)&&Ht[x]!=Ht[v]+1) continue;
int k=Init?w:min(w,Ex[x]);
if(v!=S&&v!=T&&!Ex[v])
B[Ht[v]].push(v),checkMax(Level,Ht[v]);
Ex[x]-=k,Ex[v]+=k,Edge[e].val-=k,Edge[e^1].val+=k;
if(!Ex[x]) return 0;
}
return 1;
}
inline void Relabel(int x)
{
Ht[x]=INF;
for(int e=Head[x];e;e=Edge[e].next)
if(Edge[e].val) checkMin(Ht[x],Ht[Edge[e].to]);
if(++Ht[x]<N)
{
B[Ht[x]].push(x);
checkMax(Level,Ht[x]);
++Gap[Ht[x]];
}
}
inline bool Bfs()
{
memset(Ht,0x3f,sizeof(Ht));
queue<int>Q;
Q.push(T),Ht[T]=0;
while(!Q.empty())
{
int u=Q.front();Q.pop();
for(int e=Head[u];e;e=Edge[e].next)
{
const int &v=Edge[e].to;
if(Edge[e^1].val&&Ht[v]>Ht[u]+1)
Ht[v]=Ht[u]+1,Q.push(v);
}
}
return Ht[S]!=INF;
}
inline int Select()
{
while(B[Level].empty()&&Level>=0) --Level;
return Level==-1?0:B[Level].top();
}
inline int Hlpp()
{
if(!Bfs()) return 0;
memset(Gap,0,sizeof(Gap));
for(int i=1;i<=N;++i)
if(Ht[i]!=INF) ++Gap[Ht[i]];
Ht[S]=N;
Push(S);
int u;
while((u=Select()))
{
B[Level].pop();
if(Push(u))
{
if(!--Gap[Ht[u]])
for(int i=1;i<=N;++i)
if(i!=S&&i!=T&&Ht[i]>Ht[u]&&Ht[i]<N+1)
Ht[i]=N+1;
Relabel(u);
}
}
return Ex[T];
}
int main()
{
// freopen("Hlpp.in","r",stdin);
// freopen("Hlpp.out","w",stdout);
read(N,M,S,T);
for(int i=1,u,v,w;i<=M;++i)
{
read(u,v,w);
addEdge(u,v,w);
}
printf("%d",Hlpp());
return 0;
}
```
---
### 多源汇最大流
很简单,建立一个超级源点 $S$ 链接所有的源点 $s’$ ,容量为 $inf$ ;建立一个超级汇点链接所有的汇点 $t’$ ,容量为 $inf$ 。然后处理增广路(跑模板)。
可能是因为太简单了吧,我没有找到模板题,就和普通的网络最大流少了一步而已。
---
## 最小割
### 割
割是一种划分,将 $V$ 划分成两个集合 $S,T$ 满足 $S\cup T=V,S\cap T=\varnothing$ 。且有 $s\in S,t\in T$ 。
### 割的容量 x 最小割
对于割 $(S,T)$ 有容量 $c(S,T)$ 表示 $c(S,T)=\sum_{u\in S,v\in T}c(u,v)$ ,即从 $S$ 到 $T$ 的边的容量之和。且有 $c(s,t)=c(S,T)$ 。
而最小割就是求一个集合划分使 $c(S,T)$ 最小。
### 最大流最小割定理
$f(s,t)_{\max}=c(s,t)_{\min}
对于任意一个可行流 f(s,t) 的割 (S,T) ,则有:
\begin{aligned}
f(s,t)=S\text{出边的总流量}-S\text{入边的总流量}\leq S\text{出边的总流量}=c(s,t)
\end{aligned}
那么,令 f 是最大流,则其残余网络中不会存在 (s,t) 的增广路,那么 S 的出边是满流,入边是零流,则:
\begin{aligned}
f(s,t)=S\text{出边的总流量}-S\text{入边的总流量}=S\text{出边的总流量}=c(s,t)
\end{aligned}
而此时的 f(s,t) 实际上是流函数 f 的 f(s,t)_{\max} 。
求割边数量
即在满足最小割的前提下,最小化割边的数量(即删除的边的数量)。首先跑最大流求出最小割,然后将没有满流的边容量改成 inf ,并将满流了的边的容量改为 1 ,重新跑一遍最小割,求出来的即是最小割边数。如果没有最小割,则直接将所有边的容量都设为 1 并跑最小割。
另外两种方法可以参考这一篇题解。
全局最小割 x Stoer-Wagner 算法
你可以把它理解为无源汇最小割,其最小割的重定义为:
去掉其中一些边能使一张网络不再连通的边集称为该网络的割。
其最小割定义为方案中边集和最小的一种方案。
使用 \text{Stoer-Wagner} 算法来解决这个问题。(因为无源汇,所以你暴力建源汇点跑 N^2 次即使是 ISAP 也是行不通的)
时间复杂度 \mathcal O(|V||E|+|V|^2\log |V|) 近似于 \mathcal O(V^3) 。
存在一个结论:
图中有任意两点 u,v ,存在 G 的任意一个割 C ,要么 u 和 v 连通,在同意连通块;要么 C 是一个 u-v 割。
流程:
1. 任意指定两点 $s,t$ 作为源汇点并求出 $C(s-t)$ ,记作 $cut\ of\ phase$ ,更新答案;
2. 合并点 $s,t$ ,如果 $|V|>1$ ,重复操作一;
3. 答案保证 $ans=\min\{cut\ of\ phase\}$ 。
合并:
> 删除边 $c(s,t)$ ,并对于 $G/\{s,t\}$ 中的 $k$ ,删除 $c(t,k)$ ,并将边权 $val(t,k)$ 加到 $val(s,k)$ 中。
#### 算法的正确性
如果 $s,t$ 在同一连通块中,则 $(k,s)\in C_{\min}$ 与 $(k,t)\in C_{\min}$ 互为充分必要条件。否则,因为 $s,t$ 连通, $k,t$ 连通,导致 $s,k$ 连通,此时 $C=C_{\min}/s$ ,将比 $C_{\min}$ 更优,反之亦然。所以 $s,t$ 可以看做同一点。
操作一考虑了 $s,t$ 不连通的情况,而 $s,t$ 解决了剩下的情况。根据操作的递归性,操作执行 $|V|-1$ 次后必然结束。
---
#### 求取 S-T 最小割
~~如果我都写出来了,说明就不能跑最大流啊。~~
当前状态下的图表示为 $G’=(V’,E’)$ ,构造一个集合记为 $A$ ,初始有 $A=\varnothing$ 。
定义权值函数为 $w(A,i)=\sum_{j\in A}val(i,j)$ ,特殊地, $val(i,j)=0,(i,j)\notin E’$ 。
遍历 $V'$ 中的所有点,若有 $i\notin A$ ,将 $w(A,i)$ 中最大的节点加入 $A$ 直到 $|A|=|V’|$ 。
所有点加入 $A$ 的顺序必然是固定的,有 $ord(i)$ 表示第 $i$ 个加入 $A$ 的点,有 $t=ord(|V’|)$ ; $pos(v)$ 表示 $v$ 被加入 $A$ 后 $|A|$ 的大小,即 $v$ 被加入的顺序。
对于任意点 $s$ ,则 $c(s-t)=w(t)$ 。
[正确性证明](https://oi-wiki.org/graph/stoer-wagner/#_6)
似乎这个算法的绝大部分代码使用的都是邻接矩阵。(至少我没有发现链式前向星和邻接表的写法)似乎可以联系 $\text{Prim}$ 算法来理解,不过 $\text{Prim}$ 我也没学过,所以不考虑。
写法参考 $\text{OI-Wiki}$。
``` c++
const int MAXN=601;
const int INF=0x7f7f7f7f;
int Fa[MAXN],Size[MAXN],Edge[MAXN][MAXN];
int Find(int x)
{
if(x==Fa[x]) return x;
return Fa[x]=Find(Fa[x]);
}
int Dist[MAXN],Vis[MAXN],Bin[MAXN];
//Bin记录该点是否被合并过
//Vis记录本次查询中是否已经被搜到过
//Dist记录当前最大权值(具体什么权值我也不太清楚)
int N,M;
inline int contract(int &s,int &t)
{
memset(Dist,0,sizeof(Dist));
memset(Vis,0,sizeof(Vis));
int k,minCut,maxCut;
for(int i=1;i<=N;++i)
{
k=maxCut=-1;
for(int j=1;j<=N;++j)
if(!Bin[j]&&!Vis[j]&&Dist[j]>maxCut)
{
k=j;
maxCut=Dist[j];
}
if(k==-1) return minCut;
s=t,t=k;
minCut=maxCut;
Vis[k]=1;
for(int j=1;j<=N;++j)
if(!Bin[j]&&!Vis[j]) Dist[j]+=Edge[k][j];
}
return minCut;
}
inline int Stoer_Wagner()
{
int i,minCut,s,t,res;
for(i=1,minCut=INF;i<N;++i)
{
res=contract(s,t);
Bin[t]=1;
if(minCut>res) minCut=res;
if(minCut==0) return 0;
for(int j=1;j<=N;++j)
if(!Bin[j]) Edge[s][j]=(Edge[j][s]+=Edge[j][t]);
}
return minCut;
}
int main()
{
// freopen("sto.in","r",stdin);
// freopen("sto.out","w",stdout);
read(N,M);
if(M<N-1)
{
printf("0");
return 0;
}
for(int i=1;i<=N;++i) Fa[i]=i,Size[i]=1;
for(int i=1,u,v,w;i<=M;++i)
{
read(u,v,w);
int uf=Find(u),vf=Find(v);
if(uf!=vf)
{
if(Size[uf]>Size[vf]) swap(uf,vf);
Fa[uf]=vf,Size[vf]+=Size[uf];
}
Edge[u][v]+=w,Edge[v][u]+=w;
}
int rf=Find(1);
if(Size[rf]!=N)
{
printf("0");
return 0;
}
printf("%d",Stoer_Wagner());
return 0;
}
```
---
### 最大权闭合图
在一个网络(图) $G=(V,E)$ 中的一个子图满足该子图中的任意点的任意一条边都不会引申到该图之外的任意节点。而最大权闭合子图就是满足上述条件,点权和最大的子图。
一般而言,这种定义都针对于有向图,如果是无向图,那么这张图唯一一个闭合图就是它本身,否则该图不连通。
那么如何求解最大权闭合图。
当然是使用网络流。(否则也不会写在这儿)
首先给出结论和做法:
1. 建立一个超级源点 $S$ 和一个超级汇点 $T$ ;
2. 对于 $\forall x\in V,pt[x]\ge 0$ ,链接 $(S,x,pt[x])$ ;
3. 对于 $\forall x\in V,pt[x]<0$ ,链接 $(x,T,-pt[x])$ 。
4. 对于 $\forall c(u,v)\in E$ ,链接 $(u,v,inf)$ 。
5. 最大权闭合图的权值等于正权点点权和减去从 $S$ 到 $T$ 的最大流。
从 $S$ 而出的是最大可获得权值(正权值和),向 $T$ 而出的是最大损失权值(负权值和)。
尽量多从 $S$ 获得的同时,避免向 $T$ 丢失。
如果选定一个点进入最大权闭合图,则这个点的所有后继点都必须被选择。
否则有悖定义。
对于我们建出来的这个图,得到的最小割必定是简单割,(即划分出来的其中一个集合有且仅有源点或者汇点)否则不是该图的最小割。
那么,从 $S$ 流出的流量则是得到的,流向 $T$ 的则是损失的。所以 $flow[S]-flow[T]$ 即是最大权。
所谓 $flow[S]$ ,就是 $\displaystyle \sum\limits_{x}^{x\in V} pt[x],pt[x]\ge 0$ 。
但如何求出 $flow[T]$ ,就是关键所在。因为对于一个点 $x$ 的后继损失不会超过该点的权值。那不妨我一开始就把所有的正权点都给选了(满足从 $S$ 流出的最多),让他们往后代流,大不了被负权子孙点损失完,而那些没有被损失完的,就是我们统计下来的结果。
最后得出结论:$flow[T]$ 就是从 $S$ 到 $T$ 的最大流(最小割)。
值得注意的一点:**最大权闭合图与最小割一一对应。**
令 $sum_+$ 为正点权和,$choose_+$ 为不选的正点权和,$choose_-$ 为选择的负点权和,则有:
$c(S,T)=choose_++|choose_-|
val_{max}=sum_+-(choose_++|choose_-|)=sum_+-c(S,T)
---
[最大权闭合图](https://www.luogu.com.cn/problem/P4174)的[双倍经验](https://www.luogu.com.cn/problem/CF1082G)。
求一个子图的边权和减去点权和。
> 那么,从 $S$ 流出的流量则是得到的,流向 $T$ 的则是损失的。所以 $flow[S]-flow[T]$ 即是最大权。
有这句话的定义,我们可以知道建图的大概方向:
1. 对于每一条边 $e$ ,链接 $(S,e)$ ,容量为边权;
2. 对于每一个点 $v$ ,链接 $(v,T)$ ,容量为点权;
3. 对于每一条边 $e(u,v)$ ,链接 $(e,u),(e,v)$ ,容量都是 $inf$ 。
答案是 $\displaystyle\sum_{e}e_w-Dinic()$ 。
点数:$|V|=N+M+2
边数:|E|=2(N+3M)
const int MAXN=5e3+10;
const int MAXM=5e4+10;
const ll INF=1145141919810;
int N,M,S,T;
struct Net
{
int next,to;ll val;
}Edge[2*MAXN+6*MAXM];
int Head[MAXN+MAXM],Cur[MAXN+MAXM],Total=1;
inline void addEdge(int u,int v,ll w)
{
Edge[++Total]=(Net){Head[u],v,w};Head[u]=Total;
Edge[++Total]=(Net){Head[v],u,0};Head[v]=Total;
}
int Fl[MAXN+MAXM];
inline bool Bfs()
{
memset(Fl,-1,sizeof(Fl));
Fl[S]=0,Cur[S]=Head[S];
std::queue<int>Q;
Q.push(S);
while(!Q.empty())
{
int u=Q.front();Q.pop();
for(int e=Head[u],v;e;e=Edge[e].next)
{
v=Edge[e].to;
if(Fl[v]==-1&&Edge[e].val)
{
Fl[v]=Fl[u]+1;Cur[v]=Head[v];
if(v==T) return 1;
Q.push(v);
}
}
}
return 0;
}
ll Dfs(int x,ll inf)
{
if(x==T) return inf;
ll flow=0;
for(int e=Cur[x],v;e&&flow<inf;e=Edge[e].next)
{
v=Edge[e].to,Cur[x]=e;
if(Fl[v]==Fl[x]+1&&Edge[e].val)
{
ll k=Dfs(v,std::min(Edge[e].val,inf-flow));
if(!k) Fl[v]=-1;
Edge[e].val-=k,Edge[e^1].val+=k,flow+=k;
}
}
return flow;
}
inline ll Dinic()
{
ll r=0,flow;
while(Bfs()) while(flow=Dfs(S,INF)) r+=flow;
return r;
}
ll sum;
int main()
{
// freopen("mincut.in","r",stdin);
// freopen("mincut.out","w",stdout);
read(N,M);
S=0,T=N+M+1;
for(int i=1;i<=N;++i)
{
ll w;read(w);
addEdge(i+M,T,w);
}
for(int i=1,u,v;i<=M;++i)
{
ll w;read(u,v,w);sum+=w;
addEdge(i,u+M,INF);
addEdge(i,v+M,INF);
addEdge(S,i,w);
}
write(sum-Dinic());
return 0;
}最大密度子图
对于一个图 G=(V,E) ,选出其一个子边集 E'\subseteq E ,在求出一个子点集 V'\subseteq V,\forall u,v\in V',(u,v)\in E' ,即 E' 集合中所有的边的两端点都必须在 V' 中。对于一个子图 G'=(V',E') 满足 \frac{\mid E'|}{|V'|} 最大,则 G' 是 G 的最大密度子图。
这让人不禁想到了 01 规划 ,所以也就采用二分求解。但是判断函数需要联系到最小割去。
再次回忆一次 01 规划的思路。
令 \frac{|E'|}{|V'|}=g ,则有 |E'|=g|V'| ,那么如果要让该式子最大,则有 \frac{|E'|}{|V'|}>g ,同理就有 |E'|-g|V'|>0 ,那么问题就可以转化为求出 |E'|-g|V'| 的最大值,或者求 g|V'|-|E'| 的最小值。
有一种方法是把求最大密度子图转化为最大权闭合图来做。但这样时间复杂度较高。
点数: |V|+|E| ,边数 3|E|+|V| 。
从最大密度子图的定义来看,它是满足了闭合图的性质的。而由边定点,对于边 e=c(u,v) ,我们可以看做有一个点 e ,有边 u 和边 v 与其相连。
建图:
从超级源点 S 到所有边点 e 链接一条容量为 1 的边;
从已知点 e_a 到已知点 e_b 链接一条容量为 inf 的边;
从所有边点 e 到超级汇点 T 链接一条容量为 g 的边。(g 是当前二分抉择)
然后跑最小割以求最大权闭合子图,求出的最大权就是 |E'|-g|V'| 的最大值。
性质法
已知算式 |E'|-g|V'| 与 g|V'|-|E'| 一一对应,且当 |E'|-g|V'| 最大时,g|V'|-|E'| 正好取得最小值,我们可以从这一方面入手。
选择的点集为 |V'| 的话,则点集内所有的边都被选择的情况,是对于当前点集最优的情况。
该性质显然,无需证明。
我们定义一个反点集 \overline{V'}=V-V' ,即所有没有选择的点的集合,并定义一个函数 deg[v] 表示 v 的度数。(即有多少条边以 v 为端点)
有:
g|V'|-|E'|=\sum_{v\in V'}g-\left(\frac{\sum_{v\in V'}deg[v]-C(V',\overline{V'})}{2}\right)
设集合内部所有点的度数之和是 sum ,那么,处于集合内部的边一定被计算了 2 次,因为该边的两个端点均在集合内。而处于集合 V' 与集合 \overline{V'} 之间的割边只被计算了一次,而这样的割边的数量就是该割的容量 C(V',\overline{V'}) ,因为原图的所有边的容量在流网络中都设置成了 1 。
变换形式,得到一个较好处理的式子:
\text{原式}=\frac{1}{2}(\sum_{v\in V'}(2g-dep[v])+C(V',\overline{V'}))
在每一次抉择时, 2g-dep[v] 的值是相等的,所以影响整个式子的唯一点就是这张图的最小割。
再说说怎么建图:(讲的不是太明白)
从每一个点往超级汇点 T 链接一条容量为 2g-deg[v]+Q 的边;
从超级源点 S 向每一个点链接一条容量为 Q 的边。
取出原图,将所有原边的容量修改为 1 。
这里的 Q 是一个常数,一个偏移量,一个满足 2g-dep[v] 是正数的任意值,一般可以取到 |E| ,即原图的边数。(Q 存在的原因是容量不能为负)
我们已知,割的容量 C(S,T) 表达式可以有三种:
s\rightarrow \overline{V'}
V'\rightarrow t
V'\rightarrow \overline{V'}
其中 V'=S-s 。
以 c_{(u,v)} 的一个 \{0,1\} 函数表示 u,v 之间是否连接,则有
C(S,T)=\sum_{v\in V'}Q+\sum_{u\in V'}(2g-deg[u]+Q)+\sum_{u\in V'}\sum_{v\in\overline{V'}}c_{(u,v)}
因为有:
而 $\sum_{v\in\overline{V'}}c_{(u,v)}$ 表示的是点 $u$ 到达集合 $V'$ 外部 $\overline{V'}$ 的边数;
相减得到点 $u$ 到达集合内部的边数 $\sum_{u\in V'}c_{(u,v)}
再次化简:
\begin{aligned}
C(S,T)
&=\sum_{v\in V'}Q+\sum_{u\in V'}(Q+2g-dep[u]+\sum_{v\in V'}c_{(u,v)})
&\\
&=\sum_{v\in\overline{V'}}Q+\sum_{u\in V'}(Q+2g-\sum_{v\in V'}c_{(u,v)})
&\\
&=\sum_{v\in V'}Q+\sum_{v\in\overline{V'}}Q+\sum_{u\in V'}2g-\sum_{u\in V'}\sum_{v\in V'}c_{(u,v)}
&\\
&=nQ+2g|V'|-2|E'|
&\end{aligned}
最后得到一个肥肠简单的式子:
C(S,T)=nQ+2(g|V'|-|E'|)
显然地,nQ 是针对全局的定值,而 \min\{g|V'|-|E'|\} 就是整道题的答案,也就有:
\min\{g|V'|-|E'|\}=\frac{1}{2}\min\{C(S,T)-nQ\}
总结全题:
点数:|V| ,边数:2|V|+|E| 。时间复杂度在于 \mathcal O(\log (l,r)\times \mathcal O(maxFlow)) ,取决于二分的值域以及跑最小割(最大流)的算法。
后来发现,二分的值域可以取 [\frac{1}{n},m] ,不过取 [0,m] 也不会有太大影响。
需要注意的是:上述所有方法都是限于无权点无权边最大密度子图问题,如果有权点或者有权边则需另加讨论。
模板题指路
const int MAXN=201,MAXM=5e3+1;
const int INF=1e9;
const double eps=1e-8;
int N,M,S,T;
struct G
{
int next,to;
double val;
G(int n=0,int t=0,double v=0):next(n),to(t),val(v){}
}Edge[MAXM<<1];
struct Eg
{
int u,v;
}Edges[MAXM<<1];
int Head[MAXN],Total=1;
int Deg[MAXN],ans,Cur[MAXN];
bool St[MAXN];
inline void addEdge(int u,int v,double w1,double w2)
{
Edge[++Total]=G(Head[u],v,w1);Head[u]=Total;
Edge[++Total]=G(Head[v],u,w2);Head[v]=Total;
}
void build(double g)
{
memset(Head,0,sizeof(Head));
Total=1;
for(int i=1;i<=M;++i) addEdge(Edges[i].u,Edges[i].v,1,1);
for(int i=1;i<=N;++i)
{
addEdge(S,i,M,0);
addEdge(i,T,M+g*2-Deg[i],0);
}
}
int Fl[MAXN];
inline bool Bfs()
{
memset(Fl,-1,sizeof(Fl));
Fl[S]=0,Cur[S]=Head[S];
queue<int>Q;
Q.push(S);
while(!Q.empty())
{
int u=Q.front();Q.pop();
for(int e=Head[u],v;e;e=Edge[e].next)
{
v=Edge[e].to;
if(Fl[v]==-1&&Edge[e].val>0)
{
Fl[v]=Fl[u]+1;
Cur[v]=Head[v];
if(v==T) return 1;
Q.push(v);
}
}
}
return 0;
}
double Dfs(int x,double inf)
{
if(x==T) return inf;
double flow=0;
for(int e=Cur[x];e&&flow<inf;e=Edge[e].next)
{
Cur[x]=e;
int v=Edge[e].to;
if(Fl[v]==Fl[x]+1&&Edge[e].val>0)
{
double k=Dfs(v,min(Edge[e].val,inf-flow));
if(k<=0) Fl[v]=-1;
Edge[e].val-=k,Edge[e^1].val+=k,flow+=k;
}
}
return flow;
}
double Dinic(double g)
{
build(g);
double r=0,flow;
while(Bfs()) while(flow=Dfs(S,INF)) r+=flow;
return r;
}
void Search(int x)
{
St[x]=1;
if(x!=S) ++ans;
for(int e=Head[x];e;e=Edge[e].next)
{
int v=Edge[e].to;
if(!St[v]&&Edge[e].val>0) Search(v);
}
}
int main()
{
// freopen("minCut.in","r",stdin);
// freopen("minCut.out","w",stdout);
while((scanf("%d%d",&N,&M))!=EOF)
{
S=0,T=N+1;
memset(Deg,0,sizeof(Deg));
memset(St,0,sizeof(St));
ans=0;
for(int i=1,u,v;i<=M;++i)
{
read(u,v);
++Deg[u],++Deg[v];
Edges[i]={u,v};
}
double l=0,r=M;
while(r-l>eps)
{
double mid=(l+r)/2;
double k=Dinic(mid);
if(M*N-k>0) l=mid;
else r=mid;
}
Dinic(l);
Search(S);
if(!ans) printf("1\n1\n");
else
{
printf("%d\n",ans);
for(int i=1;i<=N;++i)
if(St[i]) printf("%d\n",i);
}
}
return 0;
}最小权点覆盖集
点覆盖集 A 是一个集合,满足图上所有边的至少一个端点都在集合内,所有点覆盖集中,总点权值最小的集合就是最小权点覆盖集。
求解是一个 \text{NP} 完全问题。即没有多项式时间复杂度的做法,有且仅有枚举暴力的实现。但在一个二分图里,有一种特殊的最小权点覆盖集。
最大权独立集
对于一般的最大权独立集而言,指的是:
在一个图 G 中选取一个点集 A ,使 A 中任意两点不相连,其中 |A| 最大的集合称为 G 的最大权独立集。
网络最大流解决二分匹配问题
二分图最大匹配(网络流算法)
构造网络流模型:
建立一个超级源点 S 与 n 中所有结点链接一条容量为 1 的边,表示一个结点只能被用 1 次;
建立一个超级汇点 T 与 m 中所有结点链接一条容量为 1 的边,表示一个结点只能匹配 1 次。
对于原图,链接 n 中的 u 与 m 中的 v ,容量为 1 。
求出该图的最大流即是该二分图的最大匹配。
const int MAXP=2001,MAXE=1e5+1;
const int INF=0x7f7f7f7f;int N,M,E,S,T;
struct G
{
int next,to,val;
G(int n=0,int t=0,int v=0):next(n),to(t),val(v){}
}Edge[MAXE<<1];
int Head[MAXP],Cur[MAXP],Total=1;
inline void addEdge(int u,int v,int w)
{
Edge[++Total]=G(Head[u],v,w);Head[u]=Total;
Edge[++Total]=G(Head[v],u,0);Head[v]=Total;
}
int Fl[MAXP];
inline bool Bfs()
{
memset(Fl,-1,sizeof(Fl));
Fl[S]=0,Cur[S]=Head[S];
queue<int>Q;
Q.push(S);
while(!Q.empty())
{
int u=Q.front();Q.pop();
for(int e=Head[u],v;e;e=Edge[e].next)
{
v=Edge[e].to;
if(Fl[v]==-1&&Edge[e].val)
{
Fl[v]=Fl[u]+1;
Cur[v]=Head[v];
if(v==T) return 1;
Q.push(v);
}
}
}
return 0;
}
int Dfs(int x,int inf)
{
if(x==T) return inf;
int flow=0;
for(int e=Cur[x],v;e&&flow<inf;e=Edge[e].next)
{
Cur[x]=e;
v=Edge[e].to;
if(Fl[v]==Fl[x]+1&&Edge[e].val)
{
int k=Dfs(v,min(Edge[e].val,inf-flow));
if(!k) Fl[v]=-1;
Edge[e].val-=k,Edge[e^1].val+=k,flow+=k;
}
}
return flow;
}
inline int Dinic()
{
int r=0,flow;
while(Bfs()) while(flow=Dfs(S,INF)) r+=flow;
return r;
}
int main()
{
// freopen("Dinic.in","r",stdin);
// freopen("Dinic.out","w",stdout);
read(N,M,E);
S=0,T=N+M+1;
for(int i=1,u,v;i<=E;++i)
{
read(u,v);
addEdge(u,M+v,1);
}
for(int i=1;i<=N;++i) addEdge(S,i,1);
for(int i=1;i<=M;++i) addEdge(i+M,T,1);
printf("%d",Dinic());
return 0;
}网络流解决二分匹配
以飞行员配对方案问题为例,最重要的是建出网络模型,然后照板子跑就好了。建出一个 S 源点和一个 T 汇点,然后链接 S 和所有外籍飞行员,链接 T 和所有英国飞行员,然后将所有能够匹配的外籍飞行员和英国飞行员链接,容量皆为 1 。最后检验一些建构出的网络的可行流和原问题的可行方案是否对应,如果是,说明建图成功,跑模板。
const int MAXN=101;
const int INF=0x7f7f7f7f;
int N,M,S,T;
struct Graph
{
int next,to,val;
Graph(int n=0,int t=0,int v=0):next(n),to(t),val(v){}
}Edge[MAXN*MAXN];
int Head[MAXN],Total=1,newTail[MAXN],Fl[MAXN];
inline void addEdge(int u,int v,int w)
{
Edge[++Total]=Graph(Head[u],v,w);Head[u]=Total;
Edge[++Total]=Graph(Head[v],u,0);Head[v]=Total;
}
inline bool Bfs()
{
queue<int>Q;
memset(Fl,0,sizeof(Fl));
Fl[S]=1;
Q.push(S);
while(!Q.empty())
{
int u=Q.front();Q.pop();
for(int e=Head[u];e;e=Edge[e].next)
if(!Fl[Edge[e].to]&&Edge[e].val)
{
Fl[Edge[e].to]=Fl[u]+1;
Q.push(Edge[e].to);
}
}
return Fl[T]!=0;
}
inline int Dfs(int x,int inf)
{
if(x==T) return inf;
int s=0;
for(int e=newTail[x];e;e=Edge[e].next)
{
newTail[x]=e;
if(Fl[Edge[e].to]==Fl[x]+1&&Edge[e].val)
{
int k=Dfs(Edge[e].to,min(inf-s,Edge[e].val));
if(k)
{
Edge[e].val-=k;
Edge[e^1].val+=k;
s+=k;
}
}
}
if(s<inf) Fl[x]=-1;
return s;
}
inline void Dinic()
{
int maxFlow=0;
while(Bfs())
{
for(int i=0;i<=N+1;++i) newTail[i]=Head[i];
maxFlow+=Dfs(S,INF);
}
if(maxFlow==0) printf("No Solution!");
else
{
printf("%d\n",maxFlow);
for(int i=2;i<=Total;i+=2)
{
if(Edge[i].to!=S&&Edge[i^1].to!=S)
if(Edge[i].to!=T&&Edge[i^1].to!=T)
if(Edge[i^1].val!=0)
printf("%d %d\n",Edge[i^1].to,Edge[i].to);
}
}
}
int main()
{
// freopen("dinic.in","r",stdin);
// freopen("dinic.out","w",stdout);
read(M,N);
int u,v;
T=N+1;
read(u,v);
while(u!=-1&&v!=-1)
{
addEdge(u,v,1);
read(u,v);
}
for(int i=1;i<=M;++i) addEdge(S,i,1);
for(int i=M+1;i<=N;++i) addEdge(i,T,1);
Dinic();
return 0;
}最小割求解最小权点覆盖集
有性质:
在二分图中,有一个特殊的性质:当所有点权都是 1 时,有最大匹配数等于最小权点覆盖集;最大权独立集等于点数减去最小权点覆盖集。
在二分图中,最小权点覆盖集解决了这一类问题:
在二分图中,对于每条边,两个端点至少选一个,求所选取的点的最小权值和。
对应方法:
二分图染色,使每一条边的端点颜色不同;
建立超级源点 S 与所有颜色为 a 的边链接一条容量为该点权值的边;
建立超级汇点 T 与所有颜色为 b 的边链接一条容量为该点权值的边。
对于二分图中原有的边,改为从 u 到 v 的容量为 inf 的边。
求取构造网络的最大流(最小割),结果则是最小点权和。 (这个结论我暂时还没有理解,但是挺好背,所以先背比较好)
最小割求解最大点权独立集
因为有:
最大权独立集等于所有点的总权值减去最小权点覆盖。
所以这两个问题其实是相通的,只是输出的答案略微不同罢了。
最大点权独立集模板题的双倍经验。
因为不能够选相邻的点,则我们将所有点分为两类使每一类不存在相邻。
建图:
对于所有 a 类点,链接 (S,a,pt[a]) ;
对于所有 b 类点,链接 (b,T,pt[b]) ;
对于相邻的点 u,v ,链接 (u,v,inf) 。
如上述方法一致。
const int MAXN=101,MAXP=2e4+1,MAXE=2e6+1;
const int INF=0x3f3f3f3f;
const int Dx[]={0,1,-1,0,0};
const int Dy[]={0,0,0,-1,1};int N,M,S,T;
struct G
{
int next,to,val;
G(int n=0,int t=0,int v=0):next(n),to(t),val(v){}
}Edge[MAXE<<1];
int Head[MAXP],Cur[MAXP],Total=1;
inline void addEdge(int u,int v,int w)
{
Edge[++Total]=G(Head[u],v,w);Head[u]=Total;
Edge[++Total]=G(Head[v],u,0);Head[v]=Total;
}
int Fl[MAXP];
inline bool Bfs()
{
memset(Fl,-1,sizeof(Fl));
Fl[S]=0,Cur[S]=Head[S];
queue<int>Q;
Q.push(S);
while(!Q.empty())
{
int u=Q.front();Q.pop();
for(int e=Head[u];e;e=Edge[e].next)
{
int v=Edge[e].to;
if(Fl[v]==-1&&Edge[e].val)
{
Fl[v]=Fl[u]+1;Cur[v]=Head[v];
if(v==T) return 1;
Q.push(v);
}
}
}
return 0;
}
int Dfs(int x,int inf)
{
if(x==T) return inf;
int flow=0;
for(int e=Cur[x];e&&flow<inf;e=Edge[e].next)
{
Cur[x]=e;
int v=Edge[e].to;
if(Fl[v]==Fl[x]+1&&Edge[e].val)
{
int k=Dfs(v,min(Edge[e].val,inf-flow));
if(!k) Fl[v]=-1;
Edge[e].val-=k,Edge[e^1].val+=k,flow+=k;
}
}
return flow;
}
inline int Dinic()
{
int r=0,flow;
while(Bfs()) while(flow=Dfs(S,INF)) r+=flow;
return r;
}
bool Color[MAXN][MAXN];
int main()
{
// freopen("netflow.in","r",stdin);
// freopen("netflow.out","w",stdout);
read(N,M);
S=0,T=N*M+1;
for(int i=1;i<=N;++i)
for(int j=1;j<=M;++j)
{
if(((i&1)&&(j&1))||((!(i&1))&&(!(j&1))))
Color[i][j]=1;
else Color[i][j]=0;
}
/*for(int i=1;i<=N;++i){
for(int j=1;j<=M;++j) cout<<Color[i][j]<<" ";
puts("");
}*/
ll Cnt=0;
for(int i=1;i<=N;++i)
for(int j=1,x;j<=M;++j)
{
read(x);
Cnt+=x;
if(Color[i][j]) addEdge(M*(i-1)+j,T,x);
else
{
addEdge(S,M*(i-1)+j,x);
for(int k=1;k<=4;++k)
{
int Nx=i+Dx[k],Ny=j+Dy[k];
if(Nx<1||Ny<1||Nx>N||Ny>M) continue;
addEdge(M*(i-1)+j,M*(Nx-1)+Ny,INF);
}
}
}
printf("%d",Cnt-Dinic());
return 0;
}上下界网络流
字面意思,对于每一条边的可行流,存在最小流 min(c(u,v)) 和最大流 max(c(u,v)) ,该边在满足最大流的所有性质的前提下,必须满足 min(c(u,v))\le f(c(u,v))\le max(c(u,v)) 。这是上下界可行流。
上下界流分为有源汇 和无源汇 两种情况。
无源汇上下界可行流
所谓可行流,就是满足容量限制,流守恒性,斜对称性的流。而对于拥有上下界的网络,其限制严格许多。
首先,下界必须流满,所以我们可以在建边时直接将容量建为 upper(x)-lower(x) ,但是又考虑到每条边的下界并不一定相等,所以,我们需要额外找出位置来平衡流量:
建立虚拟源点和虚拟汇点。
令虚拟源点为 vS ,虚拟汇点为 vT ,对于点 x 流入的流量为 in_x ,流出的流量为 out_x 。出入的流量差记为 dif[x],dif[x]=in_x-out_x 。则有:
这样其实就变成了一个常规的有源汇网络,然后跑最大流即可(毕竟最大流也是一种特殊的可行流)。如果跑得出来,那么除了 vS 和 vT 之外的所有点的容量应当是守恒的,则说明原图存在可行流。
模板无源汇上下界可行流
const int MAXN=501,MAXM=2e5+1;
const int INF=0x7f7f7f7f;
int N,M,vS,vT;
struct Graph
{
int next,to,val;
Graph(int n=0,int t=0,int v=0):next(n),to(t),val(v){}
}Edge[MAXM<<1];
int Head[MAXN],Cur[MAXN],Lo[MAXM<<1],Total=1;
inline void addEdge(int u,int v,int lo,int up)
{
Edge[++Total]=Graph(Head[u],v,up-lo);Lo[Total]=lo;Head[u]=Total;
Edge[++Total]=Graph(Head[v],u,0);Head[v]=Total;
}
int Fl[MAXN],Dif[MAXN];
inline bool Bfs()
{
memset(Fl,-1,sizeof(Fl));
Fl[vS]=0,Cur[vS]=Head[vS];
queue<int>Q;
Q.push(vS);
while(!Q.empty())
{
int u=Q.front();Q.pop();
for(int e=Head[u];e;e=Edge[e].next)
{
int v=Edge[e].to;
if(Fl[v]==-1&&Edge[e].val)
{
Fl[v]=Fl[u]+1;
Cur[v]=Head[v];
if(v==vT) return 1;
Q.push(v);
}
}
}
return 0;
}
int Dfs(int x,int inf)
{
if(x==vT) return inf;
int flow=0;
for(int e=Cur[x];e&&flow<inf;e=Edge[e].next)
{
Cur[x]=e;
int v=Edge[e].to;
if(Fl[v]==Fl[x]+1&&Edge[e].val)
{
int k=Dfs(v,min(Edge[e].val,inf-flow));
if(!k) Fl[v]=-1;
Edge[e].val-=k,Edge[e^1].val+=k,flow+=k;
}
}
return flow;
}
inline int Dinic()
{
int r=0,flow;
while(Bfs()) while(flow=Dfs(vS,INF)) r+=flow;
return r;
}
int main()
{
// freopen("unset-flow.in","r",stdin);
// freopen("unset-flow.out","w",stdout);
read(N,M);
vS=0,vT=N+1;
for(int i=1,u,v,lo,up;i<=M;++i)
{
read(u,v,lo,up);
addEdge(u,v,lo,up);
Dif[u]-=lo,Dif[v]+=lo;
}
int Tot=0;
for(int i=1;i<=N;++i)
if(Dif[i]>0) addEdge(vS,i,0,Dif[i]),Tot+=Dif[i];
else if(Dif[i]<0) addEdge(i,vT,0,-Dif[i]);
if(Dinic()!=Tot) printf("NO");
else
{
puts("YES");
for(int e=2;e<=M*2;e+=2)
printf("%d\n",Edge[e^1].val+Lo[e]);
}
// for(int e=1;e<=M*2;++e) printf("%d ",Lo[e]);
return 0;
}有源汇上下界可行流
有给定的源点和汇点,求该网络的可行流。
凡事讲究一个推进,所以我们选择将有源汇的问题转化为无源汇的问题。首先,对于有源汇的问题而言,其与无源汇问题最大的不同就在于其 S 源点的流量与 T 汇点的流量一定不同。那么,我们就需要使其相同:
连接一条从 T 到 S 上界为 inf 下界为 0 的边。这样就会使流量守恒定律一样满足于源汇点了。
有源汇上下界最小/最大流
最大流
首先跑出一条可行流,对于虚拟源点 vS 到虚拟汇点 vT 的边已经流满,但是通过定义:最大流 = 可行流 + 向上浮动的流量。所以我们要在残余网络中尽量跑满上限。
而我们需要在原图的源汇路径上重找增广路,可以得到结论是向上浮动的流量就是真实源点 S 到真实汇点 T 的最大流。
注意:跑最后一次最大流时需要把边 (T,S,inf) 删掉。
模板有源汇上下界最大流
const int MAXN=501,MAXM=2e4+1;
const int INF=0x7f7f7f7f;
int N,M,S,T,Sv,Tv;
struct Graph
{
int next,to,val;
Graph(int n=0,int t=0,int v=0):next(n),to(t),val(v){}
}Edge[MAXM<<1];
int Head[MAXN],Cur[MAXN],Total=1;
inline void addEdge(int u,int v,int w)
{
Edge[++Total]=Graph(Head[u],v,w);Head[u]=Total;
Edge[++Total]=Graph(Head[v],u,0);Head[v]=Total;
}
int A[MAXN],Fl[MAXN];
inline bool Bfs()
{
memset(Fl,-1,sizeof(Fl));
Fl[Sv]=0,Cur[Sv]=Head[Sv];
queue<int>Q;
Q.push(Sv);
while(!Q.empty())
{
int x=Q.front();Q.pop();
for(int e=Head[x];e;e=Edge[e].next)
{
int v=Edge[e].to;
if(Fl[v]==-1&&Edge[e].val)
{
Fl[v]=Fl[x]+1;
Cur[v]=Head[v];
if(v==Tv) return 1;
Q.push(v);
}
}
}
return 0;
}
int Dfs(int x,int inf)
{
if(x==Tv) return inf;
int flow=0;
for(int e=Cur[x];e&&flow<inf;e=Edge[e].next)
{
Cur[x]=e;
int v=Edge[e].to;
if(Fl[v]==Fl[x]+1&&Edge[e].val)
{
int k=Dfs(v,min(Edge[e].val,inf-flow));
if(!k) Fl[v]=-1;
Edge[e].val-=k,Edge[e^1].val+=k,flow+=k;
}
}
return flow;
}
inline int Dinic()
{
int r=0,flow;
while(Bfs()) while(flow=Dfs(Sv,INF)) r+=flow;
return r;
}
int main()
{
// freopen("maxflow.in","r",stdin);
// freopen("maxflow.out","w",stdout);
read(N,M,S,T);
Sv=0,Tv=N+1;
for(int i=1,u,v,w,c;i<=M;++i)
{
read(u,v,w,c);
addEdge(u,v,c-w);
A[u]-=w,A[v]+=w;
}
int Tot=0;
for(int i=1;i<=N;++i)
if(A[i]>0) addEdge(Sv,i,A[i]),Tot+=A[i];
else if(A[i]<0) addEdge(i,Tv,-A[i]);
addEdge(T,S,INF);
if(Dinic()<Tot) puts("please go home to sleep");
else
{
int res=Edge[Total].val;
Sv=S,Tv=T;
Edge[Total].val=Edge[Total-1].val=0;
printf("%d\n",res+Dinic());
}
return 0;
}最小流
从代码的角度来讲,最小流代码与最大流代码只有 2 处不同。
把上下界最大流比作是“榨干”,那上下界最小流就是把残余网络“退钱”。——\text{yxc}
所以,最后从 T 向 S 跑一遍最大流,再把第一次跑的最大流减去跑的第二次最大流就是原图的最小流了。
也要删去最后一条边!!
模板有源汇上下界最小流
const int MAXN=1e5+1,MAXM=3e5+1;
const int INF=0x7f7f7f7f;
int N,M,S,T,vS,vT;
struct Graph
{
int next,to,val;
Graph(int n=0,int t=0,int v=0):next(n),to(t),val(v){}
}Edge[MAXM<<1];
int Head[MAXN],Cur[MAXN],Total=1;
inline void addEdge(int u,int v,int w)
{
Edge[++Total]=Graph(Head[u],v,w);Head[u]=Total;
Edge[++Total]=Graph(Head[v],u,0);Head[v]=Total;
}
int Fl[MAXN],A[MAXN];
inline bool Bfs()
{
memset(Fl,-1,sizeof(Fl));
Fl[vS]=0,Cur[vS]=Head[vS];
queue<int>Q;
Q.push(vS);
while(!Q.empty())
{
int u=Q.front();Q.pop();
for(int e=Head[u];e;e=Edge[e].next)
{
int v=Edge[e].to;
if(Fl[v]==-1&&Edge[e].val)
{
Fl[v]=Fl[u]+1;
Cur[v]=Head[v];
if(v==vT) return 1;
Q.push(v);
}
}
}
return 0;
}
int Dfs(int x,int inf)
{
if(x==vT) return inf;
int flow=0;
for(int e=Cur[x];e&&flow<inf;e=Edge[e].next)
{
Cur[x]=e;
int v=Edge[e].to;
if(Fl[v]==Fl[x]+1&&Edge[e].val)
{
int k=Dfs(v,min(Edge[e].val,inf-flow));
if(!k) Fl[v]=-1;
Edge[e].val-=k,Edge[e^1].val+=k,flow+=k;
}
}
return flow;
}
inline int Dinic()
{
int r=0,flow;
while(Bfs()) while(flow=Dfs(vS,INF)) r+=flow;
return r;
}
int main()
{
// freopen("minflow.in","r",stdin);
// freopen("minflow.out","w",stdout);
read(N,M,S,T);
vS=0,vT=N+1;
for(int i=1,u,v,up,lo;i<=M;++i)
{
read(u,v,lo,up);
addEdge(u,v,up-lo);
A[u]-=lo,A[v]+=lo;
}
int Tot=0;
for(int i=1;i<=N;++i)
if(A[i]>0) addEdge(vS,i,A[i]),Tot+=A[i];
else if(A[i]<0) addEdge(i,vT,-A[i]);
addEdge(T,S,INF);
if(Dinic()<Tot) printf("please go home to sleep");
else
{
int res=Edge[Total].val;
vS=T,vT=S; //不同点1
Edge[Total].val=Edge[Total-1].val=0;
printf("%d",res-Dinic()); //不同点2
}
return 0;
}费用流
最小费用最大流
不同于最大流的普通网络,对于每一条边,除了源初的 c(u,v) 表示容量限制以外,还存在一个单位流量的费用表示 w(u,v) 。即流过 1 个单位流量所花费的费用。
则有当边 (u,v) 流过 f(u,v) 的流量时,就需要支付 f(u,v)\times w(u,v) 的费用。
在一个网络中花费最小的最大流称为**最小费用最大流**。一般是在最大化 $\sum\limits_{(s,v)\in E}f(s,v)$ 的前提下最小化 $\sum\limits_{(u,v)\in E}f(u,v)\times w(u,v)$ 。
---
### SSP 算法
$\text{Successive Shortest Path}$ 算法是基于贪心的算法,每次寻找单位费用最小的增广路进行增广以满足当前费用最小,直到图不存在增广路。
**SSP 算法不能求解负圈**,如果存在单位费用为负的圈(即负圈),则需要先使用消圈算法消除图上的负圈。
$\text{SSP}$ 的算法时间复杂度取决于求最短路的时间复杂度和寻找增广路的时间复杂度,设网络的最大流为 $f$ ,寻找增广路的时间复杂度为 $\mathcal O(nm)$ ,则上界的时间复杂度为 $\mathcal O(nmf)$ 。而事实上,该算法是**伪多项式时间**的。(关于值域的多项式)
对于 $\text{SSP}$ 的实现,只需将 $\text{EK,Dinic}$ 寻找增广路的算法替换为使用最短路算法寻找单位费用最小的增广路即可。($\text{EK}$ 我就不写了)
注意费用流的建边操作满足:
对于有向边 $(u,v,w,c)$ ,其中 $w$ 为流量, $c$ 为费用;则其反边则为 $(v,u,0,-c)$ 。
``` c++
const int MAXN=5e3+1;
const int MAXM=1e5+1;
const int INF=0x3f3f3f3f;
int N,M,S,T;
struct Net
{
int next,to,val,cost;
Net(int n=0,int t=0,int v=0,int c=0):
next(n),to(t),val(v),cost(c){}
}Edge[MAXM<<1];
int Head[MAXN],Cur[MAXN],Total=1;
inline void addEdge(int u,int v,int w,int c)
{
Edge[++Total]=Net(Head[u],v,w,c);Head[u]=Total;
Edge[++Total]=Net(Head[v],u,0,-c);Head[v]=Total;
}
int Dist[MAXN],ret;
bool Vis[MAXN];
inline bool Spfa(int s,int t)
{
memset(Dist,0x3f,sizeof(Dist));
memcpy(Cur,Head,sizeof(Head));
queue<int>Q;
Q.push(s),Dist[s]=0,Vis[s]=1;
while(!Q.empty())
{
int u=Q.front();Q.pop();
Vis[u]=0;
for(int e=Head[u];e;e=Edge[e].next)
{
int v=Edge[e].to;
if(Edge[e].val&&Dist[v]>Dist[u]+Edge[e].cost)
{
Dist[v]=Dist[u]+Edge[e].cost;
if(!Vis[v]) Q.push(v),Vis[v]=1;
}
}
}
return Dist[t]!=INF;
}
int Dfs(int x,int inf)
{
if(x==T) return inf;
Vis[x]=1;
int flow=0;
for(int e=Cur[x];e&&flow<inf;e=Edge[e].next)
{
Cur[x]=e;
int v=Edge[e].to;
if(!Vis[v]&&Edge[e].val&&Dist[v]==Dist[x]+Edge[e].cost)
{
int k=Dfs(v,min(Edge[e].val,inf-flow));
if(k)
{
ret+=k*Edge[e].cost;
Edge[e].val-=k,Edge[e^1].val+=k,flow+=k;
}
}
}
Vis[x]=0;
return flow;
}
inline int Dinic()
{
int res=0,flow;
while(Spfa(S,T)) while(flow=Dfs(S,INF)) res+=flow;
return res;
}
int main()
{
// freopen("mincost-maxflow.in","r",stdin);
// freopen("mincost-maxflow.out","w",stdout);
read(N,M,S,T);
for(int i=1,u,v,w,c;i<=M;++i)
{
read(u,v,w,c);
addEdge(u,v,w,c);
}
int ans=Dinic();
printf("%d %d",ans,ret);
return 0;
}
```
---
### Primal-Dual 原始对偶算法
这个算法似乎和 $\text{Johnson}$ 全源最短路 有些许类似。(看到这句话我还去学了一下 $\text{Johnson}$ 全源最短路算法)
因为费用流的时间复杂度受限于其求最短路的时间,而最快的算法 $\text{Dijkstra}$ 却无法使用(因为存在负费用),那么,我们为每一个点设置一个势能使所有的费用都变成非负值,这点类似于 $\text{Johnson}$ 算法,从而使费用流的计算可以应用 $\text{Dijkstra}$ 算法。
与 $\text{Johnson}$ 相似,首先跑一次最短路,求出源点到任意点的最短距离,即该点的初始势能 $h_i$ 。然后将边 $(u,v,c)$ 处理成 $(u,v,w+h_u-h_v)$ 即可。
与常规的最短路问题不同的是,每次增广后图的形态会发生变化,这种情况下各点的势能需要更新。
令增广之后 $S$ 到 $i$ 点的最短距离为 $d_i'$ (边权重置之后),然后将 $h_i$ 加上 $d_i'$ 即可。这样可以使图上所有边的边权均为非负。
对于原有的边,增广之前有 $d_i'+(c(i,j)+h_i-h_j)-d_j'\ge 0$ ,因此 $c(i,j)+(d_i'+h_i)-(d_j'+h_j)\ge 0$ ,即用 $h_i+d_i'$ 作为新势能并不会使 $(i,j)$ 的边权变为负。
对于该算法求增广路,可以用一个结构体 $p[v]=\{u,e\}$ 表示这一条增广路走到 $v$ 时的起点是 $u$ ,边的编号是 $e$ ,然后就可以用一个逆推来移除增广路。
可以对比一下两种方法的时间:
| 算法 | 朴素 | $\text{O}_2$ |
| :----------: | :-----: | :----------: |
| $\text{SSP}$ | $1.40s$ | $1.10s$ |
| $\text{Primal-Dual}$ | $\text{2.25s}$ | $\text{507ms}$ |
``` c++
const int MAXN=5e3+1;
const int MAXM=5e4+1;
const int INF=0x3f3f3f3f;
int N,M,S,T;
struct Net
{
int next,to,val,cost;
Net(int n=0,int t=0,int v=0,int c=0):
next(n),to(t),val(v),cost(c){}
}Edge[MAXM<<1];
struct Que
{
int now,d;
Que(int n=0,int d=0):now(n),d(d){}
bool operator<(const Que& a)const
{
return d>a.d;
}
};
struct Node
{
int v,e;
Node(int v=0,int e=0):v(v),e(e){}
}P[MAXN];
int Head[MAXN],Cur[MAXN],Total=1;
inline void addEdge(int u,int v,int w,int c)
{
Edge[++Total]=Net(Head[u],v,w,c);Head[u]=Total;
Edge[++Total]=Net(Head[v],u,0,-c);Head[v]=Total;
}
int Dist[MAXN],H[MAXN],MaxF,MinC;
bool Vis[MAXN];
inline bool Dijkstra()
{
priority_queue<Que>Q;
memset(Dist,0x3f,sizeof(Dist));
memset(Vis,0,sizeof(Vis));
Dist[S]=0;Q.push(Que(S,0));
while(!Q.empty())
{
int u=Q.top().now;Q.pop();
if(Vis[u]) continue;
Vis[u]=1;
for(int e=Head[u];e;e=Edge[e].next)
{
int v=Edge[e].to,Nc=Edge[e].cost+H[u]-H[v];
if(Edge[e].val&&Dist[v]>Dist[u]+Nc)
{
Dist[v]=Dist[u]+Nc;
P[v]=Node(u,e);
if(!Vis[v]) Q.push(Que(v,Dist[v]));
}
}
}
return Dist[T]!=INF;
}
inline void Spfa()
{
queue<int>Q;
memset(H,0x3f,sizeof(H));
H[S]=0,Vis[S]=1;
Q.push(S);
while(!Q.empty())
{
int u=Q.front();Q.pop();
Vis[u]=0;
for(int e=Head[u];e;e=Edge[e].next)
{
int v=Edge[e].to;
if(Edge[e].val&&H[v]>H[u]+Edge[e].cost)
{
H[v]=H[u]+Edge[e].cost;
if(!Vis[v])
{
Vis[v]=1;
Q.push(v);
}
}
}
}
}
int main()
{
// freopen("primal-dual.in","r",stdin);
// freopen("primal-dual.out","w",stdout);
read(N,M,S,T);
for(int i=1,u,v,w,c;i<=M;++i)
{
read(u,v,w,c);
addEdge(u,v,w,c);
}
Spfa();
while(Dijkstra())
{
int MinF=INF;
for(int i=1;i<=N;++i) H[i]+=Dist[i];
for(int i=T;i!=S;i=P[i].v) checkMin(MinF,Edge[P[i].e].val);
for(int i=T;i!=S;i=P[i].v)
{
Edge[P[i].e].val-=MinF;
Edge[P[i].e^1].val+=MinF;
}
MaxF+=MinF;
MinC+=MinF*H[T];
}
printf("%d %d",MaxF,MinC);
return 0;
}
```
---
### 最大费用最大流
其实这个东西也很简单,对于原来的费用网络,我们在构造网络的时候把每一条边的费用都取为 $-c$ ,然后跑一遍最小费用最大流,这个时候的费用是一个极小的负数,也就是原来费用网络中的最大费用最大流的答案的相反数,输出 $-ret$ 即可。
### 有源汇上下界最小费用可行流
~~应该是套娃极限了。~~
其模型基于**最小费用最大流**和**有源汇上下界可行流**。所以将上下界网络转换为通常网络,然后套上费用流的模型即可。
> 先建一个有源汇上下界最大流的图,边权加上费用,然后加上所有的下界和对应费用的乘积之和,为了让有源汇上下界最大流的图中虚点间的边满流,就选用最小费用最大流,直接跑最小费用最大流即可,如果没有满流那就无解,最后答案是求出来的最小费用最大流的费用和与先前已经计算的下界和对应费用乘积之和。
>
> 摘自 $\text{Csdn}$ 博客。
对于一条边,我们需要存储 $(u,c,l,r,c)$ ,表示起点,终点,下界,上界和费用。
与上下界网络流一样,建立虚拟源汇点 $vS,vT$ ,然后就可以开始建图了:
1. 对于边 $(u,v,l,r,c)$ ,链接 $(u,v)$ ,容量为 $r-l$ ,费用为 $c$ ;
2. 记录 $A[i]$ 表示流量差,根据 $A[i]$ 的不同链边。通俗地讲,$A[i]$ 表示流入下界和与流出下界和的差。
1. 若 $A[i]>0$ ,则链接 $(vS,i)$ ,容量为 $A[i]$ ,费用为 $0$ ;
2. 若 $A[i]<0$ ,则链接 $(i,vT)$ ,容量为 $-A[i]$ ,费用为 $0$ 。
3. 链接 $(T,S)$ ,容量为 $inf$ ,费用为 $0$ 。
第三步很好理解,把有源汇转化为无源汇。
然后记录答案为 $ret=\operatorname{SSP}(vS,vT)$ ,当然,只要是最小费用最大流的算法都可以。
最后答案就是 $\displaystyle ret+\sum lower(e)\times e_c$ 。
即求出的费用加上原图中边下界与边费用的积。
**注意:这里的流不一定是最大流。**
---
### P4553
跑了一圈发现基本上都没几个写 $\operatorname{SSP-Dinic}$ 的,要么是 $\operatorname{SSP-EK}$ ,要么直接暴力推流。总之,说说建图:
1. 拆点,将每个国家拆为出入两点,链接 $(in_e,out_e)$ ,容量 $[v_e,v_e]$ ,固定容量;
2. 建立虚拟结点 $Ex$ ,链接 $(vS,Ex)$ ,容量为 $[m,m]$ ,并链接 $(Ex,e)$ ,容量为 $[0,inf]$ ;
3. 链接 $(out_e,vT)$ ,容量 $[0,inf]$ 。
4. 对于道路,链接 $(i,j)$ ,容量 $[0,inf]$ ,费用为机票费用。
然后,这道题也可以不用上下界(其实上下界本身的解题思路就是化上下界为通常)。下面就是常规费用流 $\operatorname{SSP-Dinic}$ 写法。
``` c++
const int MAXN=5e2+10;
const int MAXM=5e5+10;
const int INF=0x3f3f3f3f;
int N,M,S,T,Ex;
struct Net
{
int next,to,val,cost;
}Edge[MAXM<<1];
int Head[MAXN],Cur[MAXN],Total=1;
inline void addEdge(int u,int v,int w,int c)
{
Edge[++Total]=(Net){Head[u],v,w,c};Head[u]=Total;
Edge[++Total]=(Net){Head[v],u,0,-c};Head[v]=Total;
}
int Dist[MAXN],ret;
bool Vis[MAXN];
inline bool Spfa(int s,int t)
{
memset(Dist,0x3f,sizeof(Dist));
memset(Vis,0,sizeof(Vis));
Dist[s]=0;
std::queue<int>Q;
Q.push(s);
while(!Q.empty())
{
int u=Q.front();Q.pop();
Vis[u]=0;
for(int e=Head[u],v;e;e=Edge[e].next)
{
v=Edge[e].to;
if(Dist[v]>Dist[u]+Edge[e].cost&&Edge[e].val)
{
Dist[v]=Dist[u]+Edge[e].cost;
if(!Vis[v]) Vis[v]=1,Q.push(v);
}
}
}
return Dist[t]!=INF;
}
int Dfs(int x,int inf)
{
if(x==T) return inf;
int flow=0;Vis[x]=1;
for(int e=Cur[x],v;e&&flow<inf;e=Edge[e].next)
{
Cur[x]=e,v=Edge[e].to;
if(!Vis[v]&&Dist[v]==Dist[x]+Edge[e].cost&&Edge[e].val)
{
int k=Dfs(v,std::min(Edge[e].val,inf-flow));
if(k)
{
Edge[e].val-=k,Edge[e^1].val+=k,flow+=k;
ret+=k*Edge[e].cost;
}
}
}
Vis[x]=0;
return flow;
}
inline int Dinic()
{
int r=0,flow;
while(Spfa(S,T))
{
memcpy(Cur,Head,sizeof(Head));
while(flow=Dfs(S,INF)) r+=flow;
}
return r;
}
int V[MAXN];
int main()
{
// freopen("upper-lower-st-mincost-netflow.in","r",stdin);
// freopen("upper-lower-st-mincost-netflow.out","w",stdout);
read(N,M);
S=0,T=N+N+1,Ex=T+1;
addEdge(S,Ex,M,0);
for(int i=1;i<=N;++i)
{
read(V[i]);
addEdge(i+N,T,V[i],0);
addEdge(Ex,i+N,INF,0);
}
for(int i=1;i<=N;++i)
{
addEdge(S,i,V[i],0);
for(int j=i+1,v;j<=N;++j)
{
read(v);
if(v==-1) continue;
addEdge(i,j+N,INF,v);
}
}
Dinic();
write(ret);
return 0;
}
```
---
### P4043
真的诶,翻遍全网居然没有写 $\operatorname{SSP-Dinic}$ 的?~~(贺都找不到地方)~~
然后就贺了一个 $\operatorname{MCMF}$ 的板子然后瞎改成了 $\operatorname{SSP-Dinic}$ 。
所谓的 $\operatorname{MCMF}$ 算法,就是暴力推流,也就是费用流的 $\operatorname{SSP-EK}$ 算法。在 $\operatorname{Spfa}$ 上无异,但是会记录一个数组 $Pre[v]$ 表示是通过编号为 $Pre[v]$ 的边转移到的 $v$ ,并用 $Incf[u]$ 记录当前增广路的流量,然后用一个逆推从 $T\sim S$ 计算答案。
这里给出 $\operatorname{MCMF}$ 的函数:
``` c++
inline void Mcmf()
{
int minCost=0;
while(Spfa())
{
int x=T;
minCost+=Dist[x]*Incf[x];
while(x!=S)
{
int e=Pre[x];
Edge[e].val-=Incf[T],Edge[e^1].val+=Incf[T];
x=Edge[e^1].to;
}
}
ret+=minCost;
}
```
然后就是名正言顺的 $\operatorname{SSP-Dinic}$ 的上下界费用流写法。(甚至以 $\text{86ms}$ 冲进了最优解)其实与上下界网络流无异,就是将 Bfs() 换成 Spfa() 即可,难点依然在建图:
1. 对于剧情 $i$ 能够到达 $u$ ,链接 $(i,u)$ ,容量为 $[1,inf]$ ,费用为 $v$ 。
2. 因为除了 $1$ 号剧情,其它所有剧情都应该能够直接结束,所以链接 $(i,T)$ ,这里的 $T$ 是真实汇点,容量为 $[0,inf]$ ,费用为 $0$ ;
3. 对于流量不守恒的点,根据 $A[i]$ 的正负,链接虚拟源点或者虚拟汇点,容量为 $\mid A[i]\mid$ ,费用为 $0$ 。
4. 链接 $(T,S)$ ,都是真实的。容量为 $[0,inf]$ ,费用为 $0$ 。
因为这里只是求取可行流,所以跑一遍即可。
``` c++
const int MAXN=1e3+10;
const int MAXM=1e6+10;
const int INF=0x3f3f3f3f;
int N,M,S,T,ret;
struct Net
{
int next,to,val,cost;
}Edge[MAXM<<1];
int Head[MAXN],Cur[MAXN],Total=1;
inline void addEdge(int u,int v,int w,int c)
{
Edge[++Total]=(Net){Head[u],v,w,c};Head[u]=Total;
Edge[++Total]=(Net){Head[v],u,0,-c};Head[v]=Total;
}
int Dist[MAXN],A[MAXN];
bool Vis[MAXN];
inline bool Spfa()
{
std::queue<int>Q;
memset(Dist,0x3f,sizeof(Dist));
memset(Vis,0,sizeof(Vis));
Q.push(S);
Dist[S]=0;
while(!Q.empty())
{
int u=Q.front();Q.pop();
Vis[u]=0;
for(int e=Head[u];e;e=Edge[e].next)
{
int v=Edge[e].to;
if(Dist[v]>Dist[u]+Edge[e].cost&&Edge[e].val)
{
Dist[v]=Dist[u]+Edge[e].cost;
if(!Vis[v]) Vis[v]=1,Q.push(v);
}
}
}
return Dist[T]!=INF;
}
int Dfs(int x,int inf)
{
if(x==T) return inf;
int flow=0;Vis[x]=1;
for(int e=Cur[x],v;e&&flow<inf;e=Edge[e].next)
{
v=Edge[e].to,Cur[x]=e;
if(!Vis[v]&&Edge[e].val&&Dist[v]==Dist[x]+Edge[e].cost)
{
int k=Dfs(v,std::min(Edge[e].val,inf-flow));
if(k)
{
ret+=k*Edge[e].cost;
Edge[e].val-=k,Edge[e^1].val+=k,flow+=k;
}
}
}
Vis[x]=0;
return flow;
}
inline int Dinic()
{
int r=0,flow;
while(Spfa())
{
memcpy(Cur,Head,sizeof(Head));
while(flow=Dfs(S,INF)) r+=flow;
}
return r;
}
int main()
{
// freopen("netflow.in","r",stdin);
// freopen("netflow.out","w",stdout);
read(N);
int rS=1,rT=N+1,vS=N+2,vT=N+3;
for(int i=1,k;i<=N;++i)
{
read(k);
for(int j=1,u,v;j<=k;++j)
{
read(u,v);
++A[u],--A[i];
ret+=v;addEdge(i,u,INF-1,v);
}
}
for(int i=2;i<=N;++i) addEdge(i,rT,INF,0);
for(int i=1;i<=N;++i)
{
if(A[i]>0) addEdge(vS,i,A[i],0);
else if(A[i]<0) addEdge(i,vT,-A[i],0);
}
addEdge(rT,rS,INF,0);
S=vS,T=vT;
Dinic();
write(ret);
return 0;
}
/*
6
2 2 1 3 2
2 4 3 5 4
2 5 5 6 6
0
0
0
*/
```
---
## 网络流的实际应用(构造网络)
如果一道题能够使用网络流来做(一般指最大流和最小割),那这道题的代码非常格式化:
1. 建图,构造出原网络;
2. 增广,并计算出答案。
结束。就这么简单……么?
网络流的板子在于其第 $2$ 步,正因如此,难点在于如何建图。
---
### 一道难题 Tree
其实可以用树型 $\operatorname{dp}$ 来解,但我们今天不谈 $\text{dp}$ 。
我们发现,如果使叶节点和根节点分离,最小的代价就是从根节点到叶节点的路径的最小边的代价。这与一条增广路是类似的,那么,我们可以把这道题转换成另外一个模型。
对于原图的根节点,则是网络的超级汇点 $S$ ,每一个叶节点都是一个汇点 $T’$ ,最后求源点到汇点的最大流。就是一个模板的多源汇最大流了,然后我们链接一个超级汇点 $T$ ,链接所有叶子汇点,求从超级源点到超级汇点的最大流。
但是,这道题的边是双向边,在开始的时候我们并不知道谁是起点谁是终点,所以我们跑一遍 $dfs$ 处理出叶节点并连边,并将双向边处理成单向边。
``` c++
const int MAXN=2e5+1;
const int MAXM=5e5+1;
const int INF=0x7f7f7f7f;
template<class T>
inline void read(T &x)
{
x=0;
char ch=gh(),t=0;
while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1)
{
read(x),read(x1...);
}
template<class T>
inline bool checkMax(T &x,T &y)
{
return x<y?x=y,1:0;
}
template<class T>
inline bool checkMin(T &x,T &y)
{
return x>y?x=y,1:0;
}
int N,S,T;
struct Net
{
int next,to,val;
Net(int n=0,int t=0,int v=0):next(n),to(t),val(v){}
}Edge[MAXM<<1];
int Head[MAXN],Cur[MAXN],Total=1;
inline void addEdge(int u,int v,int w)
{
Edge[++Total]=Net(Head[u],v,w);Head[u]=Total;
}
int Fl[MAXN];
inline bool Bfs()
{
memset(Fl,-1,sizeof(Fl));
Fl[S]=0,Cur[S]=Head[S];
queue<int>Q;
Q.push(S);
while(!Q.empty())
{
int u=Q.front();Q.pop();
for(int e=Head[u];e;e=Edge[e].next)
{
int v=Edge[e].to;
if(Fl[v]==-1&&Edge[e].val)
{
Fl[v]=Fl[u]+1;
Cur[v]=Head[v];
if(v==T) return 1;
Q.push(v);
}
}
}
return 0;
}
int Dfs(int x,int inf)
{
if(x==T) return inf;
int flow=0;
for(int e=Cur[x];e&&flow<inf;e=Edge[e].next)
{
Cur[x]=e;
int v=Edge[e].to;
if(Fl[v]==Fl[x]+1&&Edge[e].val)
{
int k=Dfs(v,min(Edge[e].val,inf-flow));
if(!k) Fl[v]=-1;
Edge[e].val-=k,Edge[e^1].val+=k,flow+=k;
}
}
return flow;
}
inline int Dinic()
{
int r=0,flow;
while(Bfs()) while(flow=Dfs(S,INF)) r+=flow;
return r;
}
void dpTree(int x,int last)
{
bool flag=0;
for(int e=Head[x],v;e;e=Edge[e].next)
{
if((v=Edge[e].to)==last) continue;
dpTree(v,x);
flag=1;
Edge[e^1].val=0; //处理双向边
}
if(!flag) //链接超级汇点
{
addEdge(x,T,INF);
addEdge(T,x,0);
}
return ;
}
int main()
{
// freopen("mxaflow.in","r",stdin);
// freopen("maxflow.out","w",stdout);
read(N,S);
T=N+1;
for(int i=2,u,v,w;i<=N;++i)
{
read(u,v,w);
addEdge(u,v,w);
addEdge(v,u,w);
}
dpTree(S,-1);
printf("%d",Dinic());
return 0;
}
/*
4 1
1 2 1
1 3 1
1 4 1
*/
```
---
### 蜥蜴
将平面二维图建立成网络。可以发现,能够流入的网络应该是 $\infty$ 的,而能够流出的流量就是该点的高度(权值)。这里会用到一种叫拆点的技巧——顾名思义,将原来的 $u $ 结点拆成 $u_{in}$ 和 $u_{out}$ 两个结点, $u_{in}$ 用来链接原来指向 $u$ 的边, $u_{out}$ 用来链接原来从 $u$ 出发的边。而链接 $u_{in}$ 和 $u_{out}$ 以保证经过 $u$ 之后只能有 $h[u]$ 只蜥蜴。
建图:
1. 对于 $h[u]\ne 0$ 的结点,链接 $(u_{in},u_{out},h[u])$ ;
2. 对于 $D(|u(x_1,y_1)|-|v(x_2,y_2|)\le d$ ,链接 $(u_{out},v_{in},inf)$ ;
3. 对于 $s[u]=L$ ,即存在蜥蜴,链接 $(S,u_{in},inf)$ ;
4. 对于 $D(|u(x_1,y_1)|-|OUTSIDE|)$ ,即达到边界,链接 $(u_{out},T,inf)$ 。
为什么所有容量都可以设成 $inf$ ?因为能够通过 $u$ 点的流,必然会经过 $(u_{in},u_{out})$ 的边,则其最多的流量必然会是 $h[u]$ ,而避免胡乱赋值导致容量变小,不如全部赋为 $inf$ 。
``` c++
const int MAXR=21;
const int MAXP=1e3+1;
const int MAXE=2e4+1;
const int INF=0x7f7f7f7f;
template<class T>
inline void read(T &x)
{
x=0;
char ch=gh(),t=0;
while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1)
{
read(x),read(x1...);
}
template<class T>
inline bool checkMax(T &x,T &y)
{
return x<y?x=y,1:0;
}
template<class T>
inline bool checkMin(T &x,T &y)
{
return x>y?x=y,1:0;
}
int R,C,D,Dth,S,T,Tot;
struct G
{
int next,to,val;
G(int n=0,int t=0,int v=0):next(n),to(t),val(v){}
}Edge[MAXE<<1];
int Head[MAXP],Cur[MAXP],Total=1;
inline void addEdge(int u,int v,int w)
{
Edge[++Total]=G(Head[u],v,w);Head[u]=Total;
Edge[++Total]=G(Head[v],u,0);Head[v]=Total;
}
int Fl[MAXP];
inline bool Bfs()
{
memset(Fl,-1,sizeof(Fl));
Fl[S]=0,Cur[S]=Head[S];
queue<int>Q;
Q.push(S);
while(!Q.empty())
{
int u=Q.front();Q.pop();
for(int e=Head[u];e;e=Edge[e].next)
{
int v=Edge[e].to;
if(Fl[v]==-1&&Edge[e].val)
{
Fl[v]=Fl[u]+1;Cur[v]=Head[v];
if(v==T) return 1;
Q.push(v);
}
}
}
return 0;
}
int Dfs(int x,int inf)
{
if(x==T) return inf;
int flow=0;
for(int e=Cur[x];e&&flow<inf;e=Edge[e].next)
{
Cur[x]=e;
int v=Edge[e].to;
if(Fl[v]==Fl[x]+1&&Edge[e].val)
{
int k=Dfs(v,min(Edge[e].val,inf-flow));
if(!k) Fl[v]=-1;
Edge[e].val-=k,Edge[e^1].val+=k,flow+=k;
}
}
return flow;
}
inline int Dinic()
{
int r=0,flow;
while(Bfs()) while(flow=Dfs(S,INF)) r+=flow;
return r;
}
char opt[MAXR];
inline int Dist(int x1,int y1,int x2,int y2)
{
return (x1-x2)*(x1-x2)+(y1-y2)*(y1-y2);
}
inline int In(int i,int j)
{
return C*(i-1)+j;
}
inline int Out(int i,int j)
{
return C*(i-1)+j+R*C;
}
int main()
{
// freopen("maxflow.in","r",stdin);
// freopen("maxflow.out","w",stdout);
read(R,C,D);
Dth=D*D;
S=0,T=2*R*C+1;
for(int i=1;i<=R;++i)
{
scanf("%s",opt+1);
for(int j=1;j<=C;++j)
if(opt[j]!='0') addEdge(In(i,j),Out(i,j),opt[j]-'0');
}
for(int i=1;i<=R;++i)
{
scanf("%s",opt+1);
for(int j=1;j<=C;++j)
if(opt[j]=='L') addEdge(S,In(i,j),1),++Tot;
}
for(int i=1;i<=R;++i)
for(int j=1;j<=C;++j)
if(i-D<1||j-D<1||i+D>R||j+D>C) addEdge(Out(i,j),T,INF);
for(int i=1;i<=R;++i)
for(int j=1;j<=C;++j)
for(int k=1;k<=R;++k)
for(int l=1;l<=C;++l)
if(Dist(i,j,k,l)<=Dth)
addEdge(Out(i,j),In(k,l),INF);
printf("%d",Tot-Dinic());
return 0;
}
/*
5 8 2
00000000
02000000
00321100
02000000
00000000
........
........
..LLLL..
........
........
*/
```
---
### 假期的宿舍
有点像二分图匹配,所以考虑最大流。
把学生看作是结点 $1\sim n$ ,床看作是结点 $n+1\sim 2n$ ,建图:
1. 如果该学生留校(包括看望的学生),链接 $S$ 与该学生;
2. 如果该学生有床,链接该学生的床和 $T$ 。
3. 链接每一位本校学生和自己的床。
4. 如果 $u$ 和 $v$ 认识,链接学生 $u$ 的人和学生 $v$ 的床。
5. 容量都是 $1$ 。
跑一遍 $\text{Dinic}$ 就好了。
``` c++
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<ctime>
#include<iomanip>
#include<queue>
#include<stack>
#include<map>
#include<vector>
#define gh() getchar()
#define re register
typedef long long ll;
using namespace std;
const int MAXP=1e3+1;
const int MAXE=2e4+1;
const int INF=0x3f3f3f3f;
template<class T>
inline void read(T &x)
{
x=0;
char ch=gh(),t=0;
while(ch<'0'||ch>'9') t|=ch=='-',ch=gh();
while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=gh();
if(t) x=-x;
}
template<class T,class ...T1>
inline void read(T &x,T1 &...x1)
{
read(x),read(x1...);
}
template<class T>
inline bool checkMax(T &x,T &y)
{
return x<y?x=y,1:0;
}
template<class T>
inline bool checkMin(T &x,T &y)
{
return x>y?x=y,1:0;
}
int N,M,S,T;
struct Net
{
int next,to,val;
Net(int n=0,int t=0,int v=0):next(n),to(t),val(v){}
}Edge[MAXE<<1];
int Head[MAXP],Cur[MAXP],Total=1;
inline void addEdge(int u,int v,int w)
{
Edge[++Total]=Net(Head[u],v,w);Head[u]=Total;
Edge[++Total]=Net(Head[v],u,0);Head[v]=Total;
}
int Fl[MAXP];
inline bool Bfs()
{
memset(Fl,-1,sizeof(Fl));
Fl[S]=0,Cur[S]=Head[S];
queue<int>Q;
Q.push(S);
while(!Q.empty())
{
int u=Q.front();Q.pop();
for(int e=Head[u],v;e;e=Edge[e].next)
{
v=Edge[e].to;
if(Fl[v]==-1&&Edge[e].val)
{
Fl[v]=Fl[u]+1;
Cur[v]=Head[v];
if(v==T) return 1;
Q.push(v);
}
}
}
return 0;
}
int Dfs(int x,int inf)
{
if(x==T) return inf;
int flow=0;
for(int e=Cur[x],v;e&&flow<inf;e=Edge[e].next)
{
Cur[x]=e;v=Edge[e].to;
if(Fl[v]==Fl[x]+1&&Edge[e].val)
{
int k=Dfs(v,min(Edge[e].val,inf-flow));
if(!k) Fl[v]=-1;
Edge[e].val-=k,Edge[e^1].val+=k,flow+=k;
}
}
return flow;
}
inline int Dinic()
{
int r=0,flow;
while(Bfs()) while(flow=Dfs(S,INF)) r+=flow;
return r;
}
int Test,Cnt;
bool In[MAXP];
inline void Solve()
{
memset(In,0,sizeof(In));Cnt=0;
memset(Head,0,sizeof(Head));Total=1;
read(N);
S=0,T=N+N+1;
for(int i=1;i<=N;++i)
{
read(In[i]);
if(In[i]) addEdge(i+N,T,1);
}
for(int i=1,x;i<=N;++i)
{
read(x);
if((!x&&In[i])||(!In[i])) addEdge(S,i,1),++Cnt;
}
for(int i=1;i<=N;++i)
{
if(In[i]) addEdge(i,i+N,1);
for(int j=1,x;j<=N;++j)
{
read(x);
if(x) addEdge(i,j+N,1);
}
}
if(Dinic()>=Cnt) printf("^_^\n");
else printf("T_T\n");
}
int main()
{
// freopen("maxflow.in","r",stdin);
// freopen("maxflow.out","w",stdout);
read(Test);
while(Test--) Solve();
return 0;
}
/*
1
3
1 1 0
0 1 0
0 1 1
1 0 0
1 0 0
*/
```
---
[全文可见](https://violeteternal.github.io/Eternity/%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0/OI/network-flow/)(不过那个博客已经废弃了,新的更新的话可以看[这个](https://lucareternity.github.io/学习笔记/Olympiad-Informatics/Note-Network-Flow/))