图论相关算法
Wonder_Fish
·
·
算法·理论
cnblogs
[2025-02-28] 更新 2-SAT,斯坦纳树,同余最短路,矩阵树。
[2025-06-11] 将最小生成树相关内容从树论移到本篇。
差分约束
用于解决一些像 x_1, x_2 \dots x_n 一些变量,还有一些形如 x_i-x_j \leq c 或者是 x_i-x_j \geq c 的限制,求一组合法解。
只要所有的限制在不等号同一侧 x_i,x_j 符号相反,就都可以表示为 x_j \leq x_i+c,发现这个东西很像最短路中的 dis_j \leq dis_i +c。所以考虑建图,对于每一个 x_j \leq x_i+c 的限制从 i 向 j 连一条边权为 c 的边,然后跑最短路。
为了防止图不连通,可以建一个超级源点向所有点连边权为 0 的边,但是这同时也限制了所有变量的值 \leq 0,并且会跑出来字典序最大的所有变量都为负的解。
有时候我们要求字典序最小的正数解,这个时候我们可以把所有变量都取反(体现为原图所有边的方向取反),然后跑字典序最大解。
P4926
限制形如 x_ik \leq x_j,这个时候可以两边同时取对数,转化为 \log_2(x_i)+\log_2(k) \leq log_2(x_j) ,然后就和上面一样了。
P7624
挺好的题。
一个环的环长没有确定时,对于跨过 n\to 1 边的限制没法用两个变量刻画(环长视为变量)。
考虑将环长 L 视为常数,然后就可以将每条限制都写成 x_i-x_j \leq kL+b 的形式,可以建出差分约束的图。感觉这一步不是特别好想。
要求这个差分约束系统有解,即不存在负环,也就是说每个环的边权和非负。注意到每个环的边权和都能表示为关于 L 的一次函数,所以最终合法的 L 一定是一段区间。
考虑找出区间的上下界,发现只要能判断此时的 L 的值对应有解,小于答案还是大于答案,就容易二分出答案区间。
有解即不存在负环,容易判断。小于或大于答案,可以随便找出当前 L 下的一个负环,并判断若要使这个负环消失 L 应该增大还是减小。这是需要算出负环对应的一次函数的斜率,判断其正负性即可(斜率一定不是 0,若是 0 则无论如何都无解)。
需要注意的是,若是运用 SPFA 最短路长度找负环,那退出时的点可能并不是环上的点,要先找到一个环上的点再去求环。
Johnson 全源最短路
一种 O(nm\log m) 的全源最短路算法。对于稠密图,直接 O(n^3) 的 floyd 跑常数小还好写,但是对于稀疏图,有时候 O(n^3) 的复杂度无法通过,我们想用更快的 O(nm\log m) 的方式跑 n 遍 dijkstra。这种想法在边权全部为正的状态下是,没问题的,但是有负权就不行了,只能用 SPFA,但是关于 SPFA,___。
Johnson 核心思想是给每个点赋一个势能 h_i,然后把每条边 (u,v) 的边权改变为 w_i+h_u-h_v,想办法把边权变正,就可以跑 dijkstra 了,最终的答案是改变边权过后的最短路减去 h_s-h_t,正确性可以参考物理的势能。
那下面的问题是如何赋这个势能,我们的目标是把所有边权变正 ,所以 w_i+h_u-h_v \geq 0,即 h_v \leq h_u+w_i,是差分约束的形式,所以在原图上跑最短路就得到每个点的 h_i,若存在负环就无解。
P5905 模板。
kruskal 及重构树
kruskal 的过程是简单贪心,即从小往大加边。这章主要讲利用到这个过程一些性质的 kruskal 重构树。
根据 kruskal 求最小生成树的过程,每次连边新建一个节点,左右儿子为当前合并的两个连通块的根,此时新建的节点为合并过后连通块的根,最终得到一颗二叉树,就是 kruskal 重构树。
常用于刻画存在边权限制时图的连通情况(“只经过边权不大于/小于某个值”或“经过的最大权值最小/最小权值最大”等),一般会转化为求两点 LCA 的点权,所以要根据需要设置点权。
kruskal 重构树上点到根的路径上的点权一般是单调的。
CF1706E
按加入顺序加入边并建立 kruskal 重构树,点权为边的加入时间。易发现两点连通所需要的最晚加入的边的编号即两点在重构树上 LCA 的点权。
线段树维护区间 LCA,用 dfs 序求 LCA 的科技可做到 O(n\log n)。
CF1628E
询问最大可能的权值,即到每个白点的路径上的最大值的最大值,所以从小到大加入所有边,建立 kruskal 重构树,每次查询 x 和所有白点的 LCA 的点权。
区间修改用线段树维护 LCA,比上一题麻烦不少。
P4197(加强版 P7834)
看到“只经过边权 \leq x 的边”,就容易想到 kruskal 重构树,点权为连起两个儿子时用的边权。查询的时候跳到最高权值 \leq x 的点后,问题就是在其子树内所有叶结点中找第 k 大的高度。
每次查询的叶结点在树上是一段连续的区间(类似 dfs 序),于是就是经典的静态区间第 k 小,主席树维护。
加强版要注意判图不连通。以及,注意倍增的时候要遍历所有重构树上的点,不只是原图上的点。
P4899
当天上午写的时候还是黑题,下午就降紫了(哭)。
枚举变身的点,就转成了两个子问题,一个是限制路径上所有点都大于等于某个值,另一个是限制所有点都小于等于某个值。
可以分别建立 kruskal 重构树,(u,v) 的边权分别为 \min(u,v),\max(u,v)。
然后对于每个询问倍增找到重构树上深度最浅的点满足限制,此时这个点的子树内所有叶子结点都是可以到达的。
只需要看两棵树内可以到达的点是否有交,排列映射,线段树维护。
平面图最小割
平面图最小割 = 对偶图最短路
P4001
求一个类似网格图的图的最小割,当然可以最小割 = 最大流然后跑 dinic,但这是个平面图,可以通过转对偶图最短路来求最小割。
建对偶图就对着原图手算编号就可以。
P7916
看上去是平面图最小割模型,数据范围显然是不准备放 dinic 过,考虑转成对偶图最短路。
$k>2$ 时,先考虑如何建对偶图:
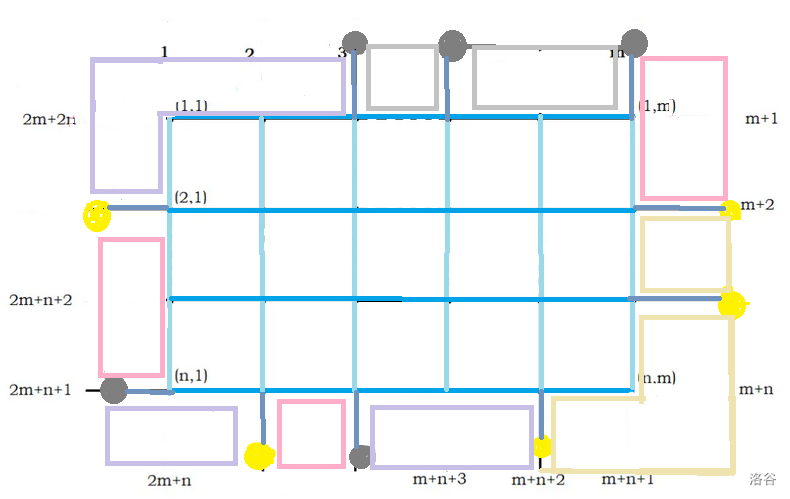
(这张图是写代码整理思路时画的,包含了各种情况,觉得删掉太浪费所以稍微修改一下放这了)
图上蓝色系(蓝,浅蓝,蓝灰)的为三种不同的边,灰点和黄点为黑白附加点,灰框黄框为黑白点内部的面,粉框和紫框为黑白点之间的面。
首先 $k$ 个附加点将外围大无界面分成了 $k$ 个无界面,无界面之间的边权(蓝灰)为附加点到原网格的边权,无界面与有界面的边权就是原来网格上的边权(蓝/浅蓝)。
然后实际上只有粉色和紫色的面可以作为起点和终点,黄色和灰色和别的面连起来不能起到分割的效果。但是黄色和灰色与有界面的边还是要连,因为可能有路径经过它。
然后接下来的问题就是选出一些起点到终点的路径,把所有黄点和灰点割开。画图发现只要起点终点一一匹配,就能完成上面的目标,具体为什么我也不太清楚,可能需要一些分类讨论。
我们可以通过最短路求出任意一对起点和终点间的距离。注意到若路径交叉,一定可以调整至不交叉,所以上述一一配对的问题可以断环为链然后类似括号匹配区间 dp。
路径之间重合一定不优,因为可以换一种匹配方式将重合段全部去掉。而这样 dp 求出的是最短的,所以不会出现重合算两次的不合法情况。
代码细节较多,注意点的编号和数组大小问题。
---
### 无向图的连通性
本部分内容较简单。实际上无向图连通性有很多复杂的问题比如边三连通分量等,但是我比较菜没有深入研究过,所以这里就不写了。
写这个时候才发现之前根本没有理解 dfs 树和塔尖,写完了可能也没完全理解。菜。
---
[P8436](https://www.luogu.com.cn/problem/P8436)
这是边双模板。求边双一般使用 tarjan,考虑 dfs 树,上面除了树边之外只有返祖边和前向边。记录时间戳 $dfn$ 和不走已走过的边能到达的最小 $dfn$ 为 $low$,对于一个点 $u$ 和其儿子 $v$ 若 $low_v > dfn_u$,那么边 $(u,v)$ 就是割边。
需要注意对于重边的判断,可以记录边的编号来保证不走已经走过的边,并且不会错误的不走重边。
关于边双的结论:
- 若 $a$ 和 $b$ 边双连通,$b$ 和 $c$ 边双连通,则 $a$ 和 $c$ 边双连通。
- $u,v$ 边双连通当且仅当 $u,v$ 之间不存在必经边。
- 边双内任意一条边 $(u,v)$ 存在经过 $(u,v)$ 的回路。
- 边双内任意一点 $u$ 存在经过 $u$ 的回路。
一般来说处理必经边问题时有时会用到边双缩点,缩完点之后是一棵树,每个点代表边双,树边是原图的割边。
---
[P8435](https://www.luogu.com.cn/problem/P8435)
点双模板。实际上和边双差不多,唯一区别在于判断条件是 $low_v \geq dfn_u$,也意味着不需要考虑回到父亲的重边问题。以及求割点的时候还需要考虑一下根节点是否是割点(具体地,若有 $\geq 2$ 个子树,为割点,仅 $1$ 个子树不为割点,否则为孤点),只需要缩点或建圆方树时直接按照算法走似乎是对的,只需注意一下是否是孤点(如果题目需要的话)。
关于点双结论:
- 两点之间任意一条路径上的所有割点,就是两点之间的所有必经点。
- 若两点双有交,那么交点一定是割点。
- 一个点是割点当且仅当它属于超过一个点双。
点双缩点看上去会比较奇怪,有一个叫(广义)圆方树的东西,可以处理点双缩点相关问题。
---
[P5058](https://www.luogu.com.cn/problem/P5058)
广义圆方树。
众所周知边双可以缩点,缩点过后是一棵树。点双连通分量不好直接缩点因为一个割点会同时属于多个点双。广义圆方树是对于每个点双建一个点(方点),连向点双内所有点(圆点)。
圆方树的性质:
- 圆点的度数等于包含它的点双的个数。
- 圆方树上圆点和方点相间。
- 圆点是叶子当且仅当它在原图上是割点。
- 圆方树上删去一个圆点后剩余节点的连通性与原图上删去这个点相同。
- 圆方树上两个点 $x,y$ 之间路径上的所有圆点为原图上 $x$ 到 $y$ 的必经点。
构建圆方树的代码:
```cpp
void tarjan(int x){
dfn[x]=low[x]=++cnt;
stk.push(x);
for(int y:g[x]){
if(!dfn[y]){
tarjan(y); low[x]=min(low[x],low[y]);
if(low[y]>=dfn[x]){
++dcc; add(x,dcc+n),add(dcc+n,x);
while(stk.top()!=y){
add(stk.top(),dcc+n),add(dcc+n,stk.top());
stk.pop();
}
add(y,dcc+n),add(dcc+n,y); stk.pop();
}
}
else low[x]=min(low[x],dfn[y]);
}
return ;
}
```
和求点双差不多。
---
[P4334](https://www.luogu.com.cn/problem/P4334)
非常适合作为点双和边双的基础练习题(bushi
对于第一问,就是问 $(G_1,G_2)$ 是否是 $A,B$ 两个点之间的割边。缩一下点,判断 $(G_1,G_2)$ 是割边且这两个点所在的边双都在 $A,B$ 所在的边双之间的路径上。
对于第二问,即询问 $C$ 是否是 $A,B$ 之间的割点。建出圆方树,看圆点 $C$ 是否在圆点 $A,B$ 之间的路径上即可。
都需要快速判断树上一个点 $Z$ 是否在 $X,Y$ 之间的简单路径上,对于这个可以通过求 LCA 判断。记 $X,Y$ 的 LCA 为 $lc$,画图发现若 $Z$ 在 $lc$ 的子树内且在 $lc$ 到 $X$ 或 $Y$ 的路径上,即 `lca(lc,z)==lc&&(lca(x,z)==z||lca(y,z)==z)` 成立时 $Z$ 在 $X$ 和 $Y$ 的简单路径上。
---
[CF487E](https://www.luogu.com.cn/problem/CF487E)
题目中有要求不能重复经过城市,从一个点双到另一个点双必然会经过割点,此时如果再回来那一定会重复经过那个割点,而在点双内不存在必经点所以可以随便走。所以点双缩点,然后树剖维护。
考虑修改操作,每次修改一个点需要修改它本身和与它相连的所有方点,对于每个方点可以开一个 `multiset` 维护。但是如果修改一个割点,那要更新所有和它相连的方点,最差复杂度是单次 $O(n)$ 这样肯定是不行的。
因此考虑一个经典 trick,定一个根,对于每个方点维护所有它的儿子节点的最小值,于是每次更新只需要更新圆点的父亲,然后询问时候如果两个点的 LCA 是方点,要额外加上 LCA 的父亲节点的贡献。
---
[P4606](https://www.luogu.com.cn/problem/P4606)
考虑建出圆方树,圆点权值为 1,方点为 0,问题转化为求这些点两两之间的路径的并的点权和减去点集的大小。
先点权转边权,最后加上 LCA 的点权。由于我不想写虚树,所以用一个结论:$\text{一个点集两两之间的路径并}=\frac{\text{按 dfs 序排序后循环相邻两点的距离和}}{2}$ 。
[P3320](https://www.luogu.com.cn/problem/P3320) 也用了同样的结论。
---
[P8456](https://www.luogu.com.cn/problem/P8456)
好题!拜谢魏老师。
正难则反,考虑补集转化,统计不合法点对。发现可以将不合法点对分为两类分别统计。
- 只含有全 `d/D`。可以去掉含有 `D/d` 的点双中的边,每个联通块内的所有点对合法。
- 含有全 `d` 和全 `D`。可证这样的点对只存在于同一个点双内,且一个点双内最多一对。充要条件是点双内恰含两点既有 `d` 边也有 `D` 边(注意是点双内的边而不是相连的所有边)。
实现上细节还是比较多的。对于求一个点双内的边,可以用一个栈存目前访问到的边,要在遍历儿子之前把边加进去。然后扫到一个点双时用类似的方式让边出栈统计。
---
[CF1763F](https://www.luogu.com.cn/problem/CF1763F)
似乎有“所有 $a\to b$ 的简单路径”这种东西的就用点双,虽然问题是必经边。
分析一下发现根据定义每个边双内不存在必经边,对于一个点双,除了只包含两点一边的东西(称为特殊点双),其它都是边双,不存在必经边,而特殊点双的边就是必经边。所以对于每次询问,只需求出 $a,b$ 之间的所有非特殊点双所含边的数量。
建出圆方树,圆点权值为 0,方点权值为点双内边数(非特殊点双)或 0(特殊点双)。每次询问就是路径上所有点权和。对于点双内边数可以用类似 [P8456](https://www.luogu.com.cn/problem/P8456) 的方式开一个栈存边来求。
一些有趣的事:思考了很长时间这个奇奇怪怪的性质有什么用,后来使用了这个和性质没有太大关系的算法通过本题。打开题解后发现第一篇第一句就是魏老师喷此题是裸题且性质没用,难绷。
---
### 有向图的连通性
一般来说都是强联通分量缩点然后 DAG 上拓扑 dp。
---
### 同余最短路
用于求解物品较少,物品体积较小,但是背包体积巨大的一些背包问题(一般来说是求可以满足的体积的数量)。
考虑任选一个基准物品 $v_p$ 来填空缺,只需要求出 $V \bmod v_p$ 的每一个取值的最小的满足条件的 $V$,就可以刻画出所有解。
考虑建图,对于每个余数值 $i$,对每个物品 $j$,连边 $(i,(i+v_j) \bmod v_p,v_j)$,跑最短路即可求出上述东西。
考虑以非图论的眼光去看待这个问题,设基准物品体积 $m$,每个物品 $v_i$ 最多会被放 $\frac{m}{\gcd(v_i,m)}-1$ 个,因为如果放了 $\frac{m}{\gcd(v_i,m)}$ 个,不如换成若干基准物品,对应到图上就是绕了一圈回到自己,显然不可能更优。
考虑加入每个物品,一个物品对应的边在图上形成了 $\gcd(m,v_i)$ 个环,对于每个环转两圈转移即可(由于不确定起点,转两圈保证了无论什么起点都能转一整圈回到自己,包含了所有转移),也可以选择最优的一个点转一圈,但是这样写起来麻烦些。这就是[同余最短路的转圈技巧](https://www.cnblogs.com/alex-wei/p/17531487.html),拜谢魏老师。
---
[P3403](https://www.luogu.com.cn/problem/P3403)
模板题,将 $x,y,z$ 中任选一个作为填补物品做同余最短路,再对每个余数算范围内的答案即可。
[P2371](https://www.luogu.com.cn/problem/P2371) 几乎一样,不必多说。
---
[ARC084B](https://www.luogu.com.cn/problem/AT_arc084_b)
很妙。
考虑一个数 $S$ 生成的过程,要求可以实时计算数字和。可以使用不进位的 $+1$ 和 $\times 10$ 两种操作生成所有数,并且不进位的 $+1$ 和 $\times 10$ 都容易计算数字和变化量。
考虑建图,对 $\bmod k \equiv i$ 的 $i$ 视为一个点,$i$ 向 $i+1$ 和 $10i$ 连边,进位的时候连上 $+1$ 边也无所谓因为一定不优。
---
[P9140](https://www.luogu.com.cn/problem/P9140)
更妙。~~当你觉得一道题很妙的时候,说明你的水平和这题还差的很远。~~
感觉并不是非常直接,最短路更新形式不太一样,需要想清楚。
题目规定 $V$ 非常大,所以会想到先用一些物品凑一个较小的值,再用一个性价比 $(\frac{c_i}{v_i})$ 最高的物品填补空缺。考虑若 $V$ 不变,确定填补物品后,对于一些已选物品,容易算出总代价。
这种填补空缺的方式容易想到同余最短路,所以考虑这种算法能不能做。
以凑成 $V$ 的代价为 $dis$ 跑最长路,如果不与 $V$ 同余算出的代价是不合法的,但是也没事,因为更新比较只在同一个余数上,算少的量相同,不会影响大小关系。
由于选的是最高性价比物品,所以加上别的物品会导致 $dis$ 减小,因此不会有正环。这其实是可以用 dij,类似全部负权边跑最长路,可以边权取反跑最短路,这里 dij 用大根堆。
对于多组询问,由于 $V$ 非常大,所以涉及到其他物品的地方策略应该是相同的。初始给 $V$ 赋一个大值算一下每个余数下的策略,询问直接用即可。
---
[P4156](https://www.luogu.com.cn/problem/P4156)
好题啊!
30pts 可以暴力同余最短路,但是朴素的同余最短路并没有优化空间。只能考虑利用一些性质去优化,然后不知道 border 的性质就输完了。
>引理:将所有 border 排序,可以划分成最多 $\log n$ 级别个等差数列子串。\
证明:所有 > $\frac{n}{2}$ 的 border,考虑其中最大的为 $l$,则原串有循环节 $d=n-l$,因此所有 >$\frac{n}{2}$ 的 border 的公差为 $d$。\
对于剩下的,取其中最大的 border $l$,则所有剩下的都是 $l$ 的 border,同理划分出所有 >$\frac{l}{2}$ 的。\
如此递归下去,每次长度折半,不会超过 $\log n$ 层。
利用这个结论,只需对每个等差数列做同余最短路,再合并即可。
对于每个等差数列 $x+kd,k\leq l$,可以把图划分为 $\gcd(x,d)$ 个部分,部分之间没有边,部分之内可以使用单调队列优化,类似转圈的方式 dp,选最优点转一圈或者随便选点转两圈即可。
考虑合并,相当于转换模数再加入若干 $x$,等价于先将 $f_i$ 映射到另一个模数上,再放入若干 $x$ 的物品,用转圈写一遍即可。
每次转圈复杂度 $O(n)$,总复杂度 $O(Tn\log n)$。代码细节较多,注意多测清空等。
---
### 2-SAT
大概就是一堆限制,每个限制形如 $x_i$ 为真/假 $\vee$ $x_j$ 为真/假,所有限制必须被满足,找一组合法解或者确定无解。
对于一组限制 $P \vee Q$,连边 $\neg P \to Q$ 和 $\neg Q \to P$,意义为若 $P$ 不被满足可以推出 $Q$ 必被满足。
然后强联通分量缩点,同一个强联通分量内部的变量取值相等,若 $x$ 和 $\neg x$ 在同一强联通分量内部显然无解。
考虑构造一组合法解,若 $x$ 所在强联通分量的拓扑序大于 $\neg x$,那么 $x$ 为真,否则 $x$ 为假。原因是若拓扑序小的为真,**可能**会推出拓扑序大的为真,但是 $x$ 和 $\neg x$ 显然不会同时为真。
---
[P4782](https://www.luogu.com.cn/problem/P4782)
照着上面说的方法建图就行。
---
[CF1675F](https://www.luogu.com.cn/problem/CF1697F)
对于每个 $a_i$ 取值为 $1 \to k$,而 $k$ 非常小 ,可以拆成 $k$ 个变量 $X_{i,j}$ 表示 $a_i$ 是否小于等于 $j$,然后 $T_{i,j}$ 向 $T_{i,j+1}$ 连边。由于 $a_i$ 单调不降,$T_{i,j} \to T_{i-1,j}$。
对于题目中的限制:
1. $a_i \neq x$ : $T_{i,x} \to T_{i,x-1}$ 。
2. $a_i+a_j \leq x$ : $F_{i,p}\to T_{j,x-p-1}$ ,$F_{j,p}$ 同理。
3. $a_i+a_j \geq x$ : $T_{i,p}\to F_{j,x-p-1}$ ,$T_{j,p}$ 同理。
以上所有的边都要连上它们的反边。
---
[P6378](https://www.luogu.com.cn/problem/P6378)
前缀和优化建图。
对于边的限制容易建图,对于一个部分的建图,边数可能直接到 $O(n^2)$ 条,会爆炸。原因在于每个点都要向其他点连边。
这样连边比较浪费,考虑加一些点简化连边。对于一个部分 $a_1,a_2,\dots,a_w$,设点 $F_i$ 表示 $a_1,a_2,\dots,a_i$ 都不选,其反点 $T_i$ 表示 $a_1,a_2,\dots,a_i$ 中恰有一点选中。
$T_i$ 需要向 $T_{i+1}$ 连边,$F_i$ 需要向 $F_{i-1}$ 连边,对于部分的限制,连 $i$ 向 $F_{i-1}$ 边及其反边即可描述限制,且边数降到了 $O(n)$。
---
[ABC210F](https://www.luogu.com.cn/problem/AT_abc210_f)
每个卡片只有两种选择,还有一些限制,容易想到 2-SAT。
设 $A_i$ 表示 $i$ 号卡片选 $a_i$,$B_i$ 表示选 $b_i$。直观的建图想法是 $n^2$ 枚举所有矛盾的点对连边,但是最坏情况下边数可能直接炸到 $n^2$,~~9e8 也不是不能过?~~,显然不可取。
考虑若 $x,y$ 不互质则 $x,y$ 一定含有相同的质因数。考虑对每个质因数,能整除它的数互相连边,可以前缀优化。而 2e6 以内每个数最多有 7 个质因数,边数是巨大常数 $O(7n)$ 的。
---
[P6965](https://www.luogu.com.cn/problem/P6965)
数据结构优化建图。
首先每个点只有最多两种选择,还有一些形如“不选 $x$ 或不选 $y$”的限制,不难想到 2-SAT,把所有可能的串中可能为前缀的连上边。
这样边数很容易炸到 $n^2$,考虑优化建图。
限制如一个字符串为另一个的前缀,可以考虑排序之后,满足 $S$ 为 $T$ 的前缀的 $T$,一定和 $S$ 靠在一起,形成一个区间。对于区间连边,可以考虑线段树优化建图。这是一种无脑大常数做法。
还有另一种更正常的想法,由前缀想到考虑 trie 树。若一个结束点为真,那么其子树里面所有结束点都为假。具体实现细节似乎比较多,所以不想写了。
---
[P5332](https://www.luogu.com.cn/problem/P5332)
容易想到每个时刻每个火星人生或死各为一个点,容易连边,但那样点数爆炸。
显然有些点并没有用,只有限制到的点才有用,只保留这些点和终止点,连边类似
连完之后,注意到是一个 DAG(生/死点内部边有序,之间只有生 $\to$ 死),不存在 SCC,也就是不存在不合法限制导致无解。
对于每一个 $j(j\neq i)$ 与一个火星人 $i$ 可以同时活到最后,当且仅当它不是必死点且 $i$生 不能到达 $j$死。
直接做是 $n^2$,可以 `bitset` 优化一下,前面的还是很好想的。
但是 `bitset` 炸空间了,考虑用一些小技巧,分块,每次处理 $B$ 个,只需要开 $B$ 位 `bitset`,$B$ 取 1e4 左右可以通过。
---
### 支配树
你说得对但是笔者只会 DAG 支配树。一般图的支配树真的会考吗???
---
[P5296](https://www.luogu.com.cn/problem/P5296)
类似上一题的转化,边权和的 $k$ 次方和相当于,从 $n-1$ 条边中选 $k$ 次求积(可以选重复的边),求所有生成树所有选法的积的和。
由于一条边会选多次,考虑维护所有生成树的边权 EGF 的积。
同样可以只保留 $\leq k$ 次的项。求逆似乎要用多项式科技,不过卷积可以直接暴力。
---
### 斯坦纳树
这个神秘的东西放在树论,图论,dp 里面似乎都不是很合适。应该算是一种关于生成树的贪心 + 最短路优化 dp。
斯坦纳树用于求解:选一个连通块,要求关键点连通(关键点一般不多),问连通块**最小**权值(所有权值非负)。
显然只连关键点是不优的,几何中就有很多反例。需要借助中间点来让权值更小。考虑最终选出来的联通块形状一定是一棵树(如果有环,删去环边不影响连通性且答案不会变劣),树上的点可能是关键点也可能不是。
发现图很大但关键点并不多。考虑树的生成过程,一棵树可以通过不断建立子节点与父节点的连边来生成。考虑状压 dp,压当前连通块包含的关键点的集合。
设 $f_{i,S}$ 表示包含关键点集合 $S$,根为 $i$ 的树的最小权值。转移分为两种:第一种换根,即存在边 $(u,v)$,$f_{u,S}\to f_{v,S}$;第二种合并根相同的子树,$f_{i,S} + f_{i,T} \to f_{i,S \cup T}$("$+$"仅表示拼接,具体情况具体考虑,不一定是加法)。发现这两种转移可以生成所有可能的树。
对于第二种转移,枚举子集即可。对于第一种,难以确定转移顺序。但是发现其形式类似最短路,贡献非负,可以用 dijkstra 或 SPFA 实现。发现较大的集合要求较小的集合答案已经算好,所以按集合从小到大转移。
注意斯坦纳树只能处理权值最小且无负权的问题。若权值最大或存在负权,第一步贪心就是错的。
---
[P6192](https://www.luogu.com.cn/problem/P6192)
纯模板。按照上面写就行。
---
[P4294](https://www.luogu.com.cn/problem/P4294)
也是模板,不过是点权,在合并操作时要减去根多算的贡献。需要输出方案。
---
[P3264](https://www.luogu.com.cn/problem/P3264)
与斯坦纳树模板区别是只要求相同频道联通,对于每个频道求斯坦纳树再加起来不一定比两个频道共用一些边更优。
考虑对每个频道集合求最小斯坦纳树再枚举子集合并。实际上每个频道集合包含的所有点都是一个关键点集合,其斯坦纳树在求全局的时候已经求过了,直接把 dp 数组的值拿来用。
---
[P3638](https://www.luogu.com.cn/problem/P3638)
毒瘤模拟+卡常题。但是一开始惯性思维把题目看错了,难绷。
考虑区间 dp,$f_{l,r,rt}$ 表示机器人 $l-r$,目前在 $rt$,所需要的最小步数。转移类似斯坦纳树,由小区间向大区间,相同区间换根,最短路优化。
预处理 $t_{i,j,0/1/2/3}$ 表示初始在 $(i,j)$,向四个方向推一下到达的格子,记忆化搜索即可求出。需要注意可能出现环,停不下来,此时是不能推的。判断可以开一个数组标记三元组 $(x,y,d)$ 是否在当前栈内,若访问到栈内元素说明有环,标记一下递归回去即可。
以上可以获得 65pts,需要继续卡常。发现边权都为 $1$,考虑使用一些神秘操作,先给 $f_{l,r}$ 排个序,开一个栈从大到小加入,从小到大扫,每次把 $f$ 为当前最小值的取出来更新,塞到栈顶,类似 dij 标记元素是否更新过其他元素。虽然还是 $\log$ 但是常数小了很多。还有关于 $f$ 的下标顺序,由于内存访问的原因,`f[l][r][id]` 要比 `f[id][l][r]` 快很多。卡完之后可以获得 100pts。
---
[P7450](https://www.luogu.com.cn/problem/P7450)
先考虑如果 $c_{i,j} \leq k$ 怎么做。
第一问是斯坦纳树的板子,每个位置权值为 $1$ 跑 dp 即可。
第二问求最小中位数考虑二分,将 $\leq mid$ 的权值赋为 $-1$,$>mid$ 赋为 $1$。然后用斯坦纳树 dp,求出包含 [0,k) 所有整数的最小连通块情况下的最小权值。
但是这样会有负权,斯坦纳树不能跑负权。由于我们实际需要的连通块大小已经固定,要想合法只需要尽量少选 $>mid$ 的东西。
所以考虑 $\leq mid$ 为 $0$,$>mid$ 为 $1$,用 `pair` 存大小和权值和,优先最小化大小 `first`,再最小化 `second`。具体实现参考了题解,用一个 1000 进制两位数,低位放权值,高位放大小。
对于 $c_{i,j}$ 很大的情况,类似 [CF1641D](https://www.luogu.com.cn/problem/CF1641D),给每个图案随机赋一个 $(0,k]$ 的权值,多做几遍取最小值即可。
单次正确的概率 $p=\frac{5!}{5^5} \approx 0.0384$,$1-p \approx 0.9616$,$(1-p)^{100}<0.02$,实际实现要做 200 次左右才能过。
本题中 SPFA 效率高于 dijkstra。