交互与提答题选讲
gaochunzhen
·
·
个人记录
作业在这里
1. 交互题
交互题分为两种:IO 交互和函数式交互。
(1) IO 交互
选手需要通过输入输出与交互器进行交互。具体来说,选手将询问等操作通过标准输出进行输出,并从标准输入中读取反馈信息。
每次输出后需要刷新缓冲区。fflush(stdout) 或 std::cout << std::flush 可以实现该操作(使用 std::cout 也可以自动刷新缓冲区)。
下面举一个例子。
P1733 猜数(IO交互版)
评测机会在区间 [1,10^9] 中选择一个整数,你应该写一个代码来猜测它。你最多可以问评测机 50 个问题。
对于每一次询问,你可以向评测机询问区间 [1,10^9] 中的一个整数,评测机会返回:
- 0,如果它为答案(即评测机所选的数字),且程序应该在此之后停止询问。
- -1,如果它小于答案。
- 1,如果它大于答案。
每次询问,你需要向标准输出输出一个 [1,10^9] 中的整数,然后清空缓冲区。
然后你需要从标准输入中输入一个整数,代表评测机返回的结果。
相信大家已经一眼秒了,所以就直接放代码了。
#include <bits/stdc++.h>
using namespace std;
int l = 1, r = 1e9, mid, x;
int main() {
while (1) {
mid = (l + r) >> 1;
printf("%d\n", mid);
fflush(stdout);
scanf("%d", &x);
if (!x) return 0;
else if (x == 1) r = mid - 1;
else l = mid + 1;
}
return 0;
}
CF843B Interactive LowerBound
先来一道简单题练练手。
有一个由 n 个元素构成的数组,其构成了一个单项链表。每个数组元素 i 包含两个整数,\mathrm{val}_i 是元素的整数值,\mathrm{nxt}_i 是它所指向的元素,如果当前元素为最后一个元素则 \mathrm{nxt}_i=-1。保证 \mathrm{val}_i 递增。
给定链表的起点 \mathrm{st} 和一个数 x,你需要求出 \geq x 的最小的 \mathrm{val}_i。
你可以询问不超过 1999 次。每次询问如下:
? i —— 询问 \mathrm{val}_i 和 \mathrm{nxt}_i。
### [题解](https://www.luogu.com.cn/blog/GCZ-Gary/cf843b-interactive-lowerbound-ti-xie)
------------
------------
### (2) 函数式交互
此类交互题需要按照出题人的要求编写一个函数,在编写的函数中可以调用题目中给出的函数进行交互。
NOI 系列赛的交互题均采用该交互方式。
**注意:在提交的代码中不需要,也不应该包含 `main` 函数,并且也不应使用标准 IO。**
在洛谷上,因为一些特殊原因,需要以特殊方式编写代码,具体写在下面:
1. 几乎所有的函数式交互题都要求选手程序包含一个指定的头文件,而在洛谷,因为一些特殊原因,选手不需要,也不应该包含这个头文件。
2. 也正是因为这个原因,为了确保程序能正常编译,选手需要在程序开头添加一些函数声明语句(这些函数都是交互库中可以供选手调用的函数)。
这里注意,在其他平台(比如 UOJ)上交的话,需要一句 `#include "xxx.h"` 的声明 **(尤其注意是 `""` 不是 `<>`)**,并且无需声明提供的函数。
按照惯例,再举一个例子。
### [P1947 猜数](https://www.luogu.com.cn/problem/P1947)
珂愛给了你一个 $[1,n]$ 之间的整数 $k$,你每次可以询问一个整数 $x$,然后珂愛会告诉你 $x$ 和 $k$ 的大小关系。
你需要用尽可能少的次数猜出珂愛想的数。
你需要实现一个函数 `int Chtholly(int n,int c)`,这个函数的作用是在不超过 $c$ 次询问中猜对 $[1,n]$ 中的一个数,返回值为你最终确定的数。
你可以调用交互库中一个叫做 `Seniorious` 的函数,其原型为 `int Seniorious(int x)`,返回值为:
- 若 $k\lt x$,则返回 $1$。
- 若 $k\gt x$,则返回 $-1$。
- 若 $k=x$,则返回 $0$。
你调用 `Seniorious` 函数的次数不超过 $c$ 才能得到这个点的分数,否则这个点为 $0$ 分。
$2\leq n\leq 10^6$,$\min(20,n-1)\leq c\leq n$。
~~相信大家还是一眼秒了,所以也直接放代码了。~~
```cpp
#include <bits/stdc++.h>
using namespace std;
extern "C" int Seniorious(int);
extern "C" int Chtholly(int n, int c) {
int l = 1, r = n;
while (l <= r) {
int mid = (l + r) >> 1;
int cmid = Seniorious(mid);
if (!cmid) return mid;
else if (cmid == 1) r = mid - 1;
else l = mid + 1;
}
return -1;
}
```
注意:因为本题中写明需要加 `extern "C"`,所以才加上,其他题目没有说明的不需要加。
------------
### [P6612 LIC-Bidding](https://www.luogu.com.cn/problem/P6612)
A 和 B 两个人在玩一个游戏,这个游戏是他们轮流操作一对整数 $(x,y)$。
初始时 $(x,y)=(1,0)$,可以进行三种操作:
1. 将 $(x,y)$ 变成 $(1,x+y)$。
2. 将 $(x,y)$ 变成 $(2x,y)$。
3. 将 $(x,y)$ 变成 $(3x,y)$。
给定正整数 $n$。在 $x+y\ge n$ 时就不能进行后两种操作。如果某个人操作后 $y\ge n$,他就输掉了。
保证给出的 $n$ 为先手必胜的,你需要提供一种先手必胜的方案。例如 $n = 3$ 时,先手选择操作 3,后手只能选择操作 1 然后输,所以 $n = 3$ 时先手必胜。
**交互题**,你需要实现一个函数 ``extern "C" int _opt(int n, int x, int y)``,该函数的返回值是一个值为 $1$,$2$ 或 $3$ 的整数,表示现在数对是 $(x, y)$,参数是 $n$ 且轮到你操作时,你会选择的操作。
$1 \leq n\leq 30000$。
### [题解](https://www.luogu.com.cn/blog/GCZ-Gary/p6612-lic-bidding-ti-xie)
------------
### [P3641 最大差分](https://www.luogu.com.cn/problem/P3641)
有 $N$ 个**严格递增**的非负整数 $a_1, a_2, \cdots, a_N$($0 \leq a_1 < a_2 < \cdots < a_N \leq 10^{18}$)。你需要找出 $a_{i + 1} - a_i$($1 \leq i \leq N - 1$)里的最大的值。
你的程序不能直接读入这个整数序列,但是你可以通过给定的函数来查询该序列的信息。关于查询函数的细节,请参考下面的实现细节部分。
你需要实现一个函数,该函数返回 $a_{i + 1} - a_i$($1 \leq i \leq N - 1$)中的最大值。
你需要实现一个函数 `findGap(T, N)`,该函数接受下面的参数,并返回一个 `long long` 类型的整数:
- $T$:子任务的编号($1$ 或者 $2$)
- $N$:序列的长度
你的函数 `findGap` 可以调用系统提供的查询函数 `MinMax(s, t, &mn, &mx)`。当 `MinMax(s, t, &mn, &mx)` 返回时,变量 `mn` 将会存储满足 $a_i \in [s, t]$ 中 $a_i$ 的最小值,变量 `mx` 将会存储满足 $a_i \in [s, t]$,$a_i$ 的最大值。如果区间 $[s, t]$ 中没有序列中的数,则 `mn` 和 `mx` 都将存储 $-1$。在查询时需要满足 $s \leq t$。
对于所有的测试点,有 $2 \leq N \leq 100000$。
每一个测试点开始测试之前,$M$ 都将被初始化为 $0$。
子任务 1:每一次调用 `MinMax` 都将使 $M$ 加 $1$。为了获得所有分数,需要满足对于该子任务下的所有测试点,都有 $M \leq \frac{N + 1}{2}$。
子任务 2:定义 $k$ 为调用 `MinMax` 时,区间 $[s, t]$ 中的序列中数的数量。每次调用 `MinMax`,将使 $M$ 加上 $k + 1$。对于每一个测试点,如果 $M \leq 3N$,你将得到所有分数。
提示:子任务 1 与子任务 2 基本无关,需要分开考虑。
### [题解](https://www.luogu.com.cn/blog/GCZ-Gary/p3641-zui-tai-ci-fen-ti-xie)
------------
## 2. 提交答案题
~~放心,没有旷野大计算。~~
提交答案题是直接提交答案的题目,通常会给出输入文件,一般会要求提交包含 `xxx1.out`、`xxx2.out` … `xxxn.out` 的压缩包。由于不需要运行源代码,所以没有具体的时空限制 ~~(取决于电脑的情况和比赛时间)~~。
### [P1008 三连击](https://www.luogu.com.cn/problem/P1008)
将 $1, 2, \ldots , 9$ 共 $9$ 个数分成 $3$ 组,分别组成 $3$ 个三位数,且使这 $3$ 个三位数构成 $1 : 2 : 3$ 的比例,试求出所有满足条件的 $3$ 个三位数。
其实就是试机题,暴搜就行。答案写在下面:
```plain
192 384 576
219 438 657
273 546 819
327 654 981
```
~~好了,想必你已经熟练掌握提交一案题了,来做两道题小试牛刀吧!~~
------------
### [P3640 出题人](https://www.luogu.com.cn/problem/P3640)
你现在是一个出题人。对于每一个子任务,会有两份代码 $A$ 和 $B$,你需要构造一组数据 $X$ 来让 $A$ 跑过、让 $B$ TLE。并且你需要保证 $X$ 中的整数个数不超过 $T$。我们仅关心用时,不考虑代码正确性。
在代码中会维护一个计数器来统计程序的操作次数。在程序的运行过程中,当该计数器超过了 $10^6$ 次时,那么我们认为程序运行超时。
现在有两种问题:
1. $\rm SSSP$:最短路
给定一个 $V$ 个点 $E$ 条边的图以及 $Q$ 个询问,每次询问包含 $(s_i,t_i)$,需要求出 $s_i\to t_i$ 的最短路长度。
$1\leq V\leq300$,边权的绝对值小于 $10^6$,$0\leq E\leq5000$,$1\leq Q\leq10$,每个点出度小于 $100$。
输入数据包含两部分,其中第一部分使用邻接表来描述带权有向图 $G$。第二部分则描述对 $G$ 的最短路径的查询。
数据第一部分的第一行包含一个整数 $V$,表示 $G$ 中点的个数,所有点的编号为 $0, 1, \cdots, V - 1$。
接下来 $V$ 行,每行描述一个点的所有边。行中的第一个整数 $n_i$ 描述了节点 $i$ 的出边数量,接下来有 $n_i$ 个整数对 $(j, w)$ 表示有一条从 $i$ 到 $j$,边权为 $w$ 的边。
数据第二部分的第一行包含一个整数 $Q$,表示询问的组数。
接下来 $Q$ 行,第 $k$ 行包含两个整数 $s_k, t_k$,为该询问对应的起点与终点位置。
2. $\rm Mystery$:无向图染色
给定一个 $V$ 个点 $E$ 条边的图,需要给每个点编号(范围为 $[0,X-1]$),使得所有直接相连的节点均有不同的编号。找出符合题意的最小的 $X$。
$70<V<1000$,$1500<E<10^6$。
输入数据的第一行包含两个整数 $V$ 和 $E$。
接下来 $E$ 行,每行两个整数 $a, b$,表示 $a$ 与 $b$ 在 $G$ 中直接相连。不允许有重边。
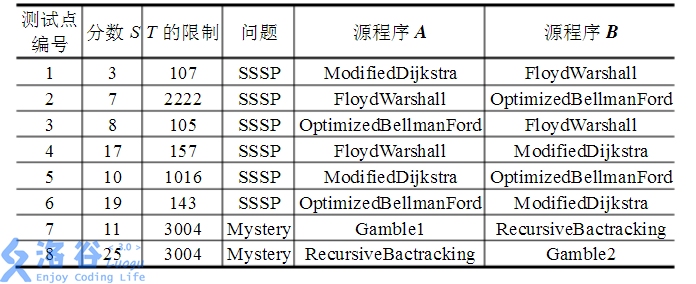
下面是程序的伪代码:
FloydWarshall
```
// pre-condition: the graph is stored in an adjacency matrix M
counter = 0
for k = 0 to V-1
for i = 0 to V-1
for j = 0 to V-1
increase counter by 1;
M[i][j] = min(M[i][j], M[i][k] + M[k][j]);
for each query p(s,t)
output M[s][t];
```
OptimizedBellmanFord
```
// pre-condition: the graph is stored in an adjacency list L
counter = 0
for each query p(s,t);
dist[s] = 0; // s is the source vertex
loop V-1 times
change = false;
for each edge (u,v) in L
increase counter by 1;
if dist[u] + weight(u,v) < dist[v]
dist[v] = dist[u] + weight(u,v);
change = true;
if change is false // this is the ’optimized’ Bellman Ford
break from the outermost loop;
output dist[t];
```
ModifiedDijkstra
```
// pre-condition: the graph is stored in an adjacency list L
counter = 0;
for each query p(s,t)
dist[s] = 0;
pq.push(pair(0, s)); // pq is a priority queue
while pq is not empty
increase counter by 1;
(d, u) = the top element of pq;
remove the top element from pq;
if (d == dist[u])
for each edge (u,v) in L
if (dist[u] + weight(u,v) ) < dist[v]
dist[v] = dist[u] + weight(u,v);
insert pair (dist[v], v) into the pq;
output dist[t];
```
Gamble1
```
Sets X = V;
labels vertex i in [0..V-1] with i;
Sets counter = 0; // will never get TLE
```
Gamble2
```
Sets X = V;
labels vertex i in [0..V-1] with i;
Sets counter = 1000001; // force this to get TLE
```
RecursiveBacktracking
```
This algorithm tries X from 2 to V one by one and stops at the first valid X.
For each X, the backtracking routine label vertex 0 with 0, then for each vertex u that has been assigned a label, the backtracking routine tries to assign
the smallest possible label up to label X-1 to its neighbor v, and backtracks if necessary.
枚举 X,直到找到一个合法的 X。
对于每个 X,先将点 0 标为 0,然后对于点 u,枚举合法的编号去 dfs + 回溯。
就是个暴搜,时间复杂度巨大,懒得算。
```
### [题解](https://www.luogu.com.cn/blog/GCZ-Gary/p3640-chu-ti-ren-ti-xie)