树链剖分(轻重链剖分)
Shunpower
·
·
个人记录
前言
Chery:我那个时代轻重链剖分需要开链数棵线段树, 2015 年的时候才有科技说开一棵线段树就够了,所以时代在进步。
树链剖分
解决的问题
- 链上操作(整条链加 x)
- 链上查询(查询整条链的和)
- 子树操作(整棵子树加 x)
- 子树查询(查询子树和)
本 blog 以括号内的内容为例,解决 P3384 【模板】轻重链剖分/树链剖分。
一些定义
- 重儿子:一个节点的所有儿子都有一个它的子树节点数,子树节点数最大的那个是重儿子。(相等的话任选一个都行)
- 轻儿子:不是重儿子的都是轻儿子。
- 重边:节点连到它重儿子的边。
- 轻边:这个节点除了重边以外的边。
- 重链:相邻重边连在一起就是重链。
重链的性质和特殊定义
$\rm Observation\ 2:$ 每一条重链的起点都是轻儿子或者根。
性质二是显然的,若是重儿子起点,那么重链一定可以继续向上取,因此重儿子绝对不会是重链的起点。
下面是一张进行重链剖分后的树图:
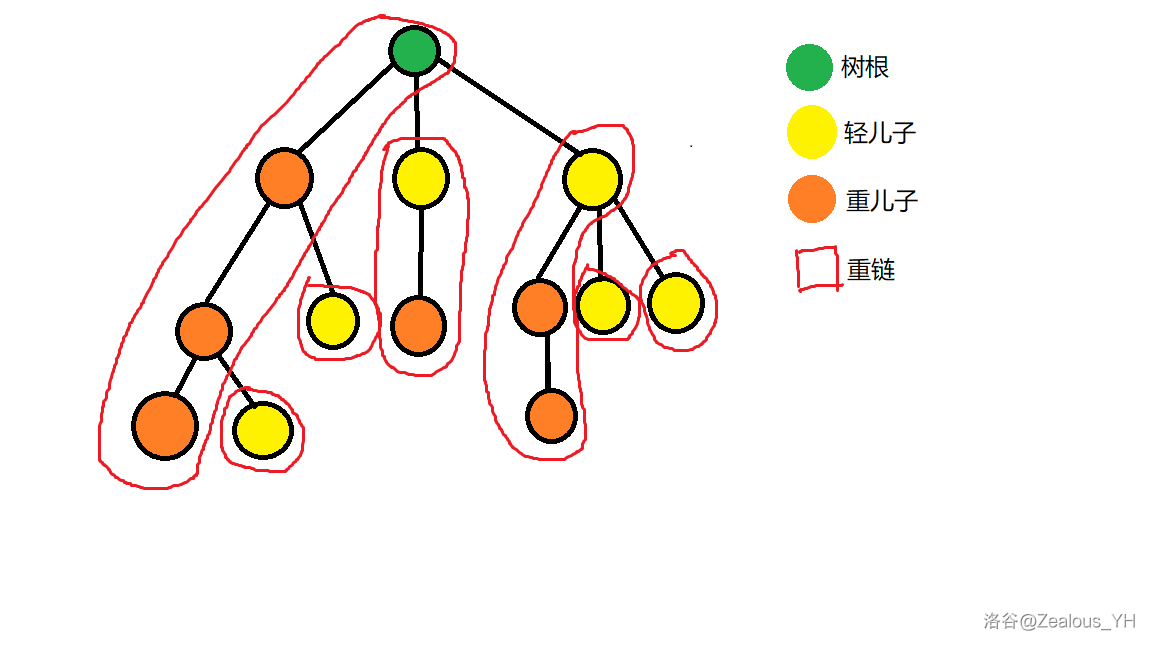
接下来怎么让程序剖就成为了问题。人眼倒是很好剖。
$\rm upd:$ @Sword_K 说,重链的条数是 $n$ 级别的,比如一朵菊花。我原来说重链条数是 $\log n$ 级别是错误的。
### 剖法
你的眼睛是怎么对树进行剖分的?你当然要先找到重儿子。
#### DFS 1
该 DFS 的作用有如下几个:
- $dep$,计算每个节点的深度(基础操作)
- $fa$,标记每个节点的父亲(基础操作)
- $sum$,记录节点子树节点数(树剖操作)
- $hson$,记录重儿子节点(树剖操作)
代码的话可以随便实现一下(随手写的,可能有错):
```
void dfs1(int x,int f){
dep[x]=dep[f]+1;//普通深度
fa[x]=f;//普通父亲
sum[x]=1;//普通子树节点数
int maxn=0;
fv(i,p[x]){
if(p[x][i]!=f){
dfs1(p[x][i],x);
if(sum[p[x][i]]>maxn){
hson[x]=p[x][i];//标记重儿子
maxn=sum[p[x][i]];
}
sum[x]+=sum[p[x][i]];//加子树节点数
}
}
}
```
#### DFS 2
接下来就要剖链了,但是树剖需要我们对节点重编号。
- $id$,标记每个节点的新编号
- $val$,把原来的节点权值赋到新编号上
- $tp$,每个节点所在重链的顶端
我们还需要使用我们之前提到的性质 $2$。
这样程序就用 $O(n)$ 的复杂度把链剖出来了,具体实现:
```
void dfs2(int x,int f,int top){
tnt++;//加编号
id[x]=tnt;//记编号
val[tnt]=w[x];//把权值扔过去
tp[x]=top;//记顶端
if(!hson[x]){//没有儿子就 return
return;
}
dfs2(hson[x],x,top);//先走重儿子(树剖关键)
fv(i,p[x]){
if(p[x][i]!=f&&p[x][i]!=hson[x]){//再走轻儿子
dfs2(p[x][i],x,p[x][i]);//每个轻儿子都是一条重链的顶端
}
}
}
```
### DFS 序相关问题
这是我们刚刚的树:
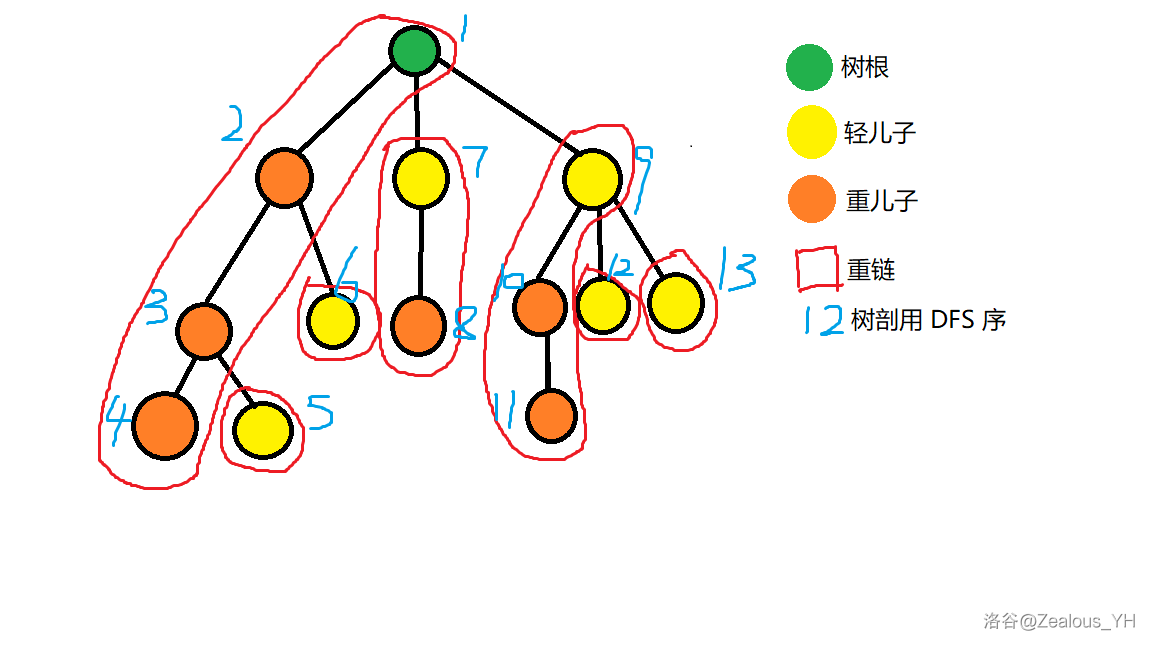
重编号之后我们观察到**很多**性质。
- $\rm Key\ Observation\ 1:$ 所有重链的编号都是连续的,而且深度递增,编号也递增。
显然,由于我们先走重儿子,所以重链上的编号是连续的。
- $\rm Key\ Observation\ 2:$ 一个子树内的编号是连续的。
DFS 的普通性质。
连续的编号相当于是区间,所以我们不妨……把问题迁移到线段树上,接下来我们的事情和原树没关系了,我们的问题转移到了刚刚的 $val$ 数组里。
### 解决问题
#### 链和
首先我们令这条链的起点、终点分别为 $x,y$。
使用 `swap` 函数令 $x$ 为**所在链顶端**深度更深的点。接着增加上 $x$ 所在链顶端到 $x$ 的权值(线段树),然后把 $x$ 变为其所在链顶端的父亲。接着重复以上操作直到 $x,y$ 在同一链上。
然后直接加上 $x$ 到 $y$ 的权值即可。注意深度越深,编号越大,如果把编号大的放在线段树的左端点处,会 $\rm \color{purple}RE$。
具体跳的方法有(零点)一丢丢像 LCA,如下图:
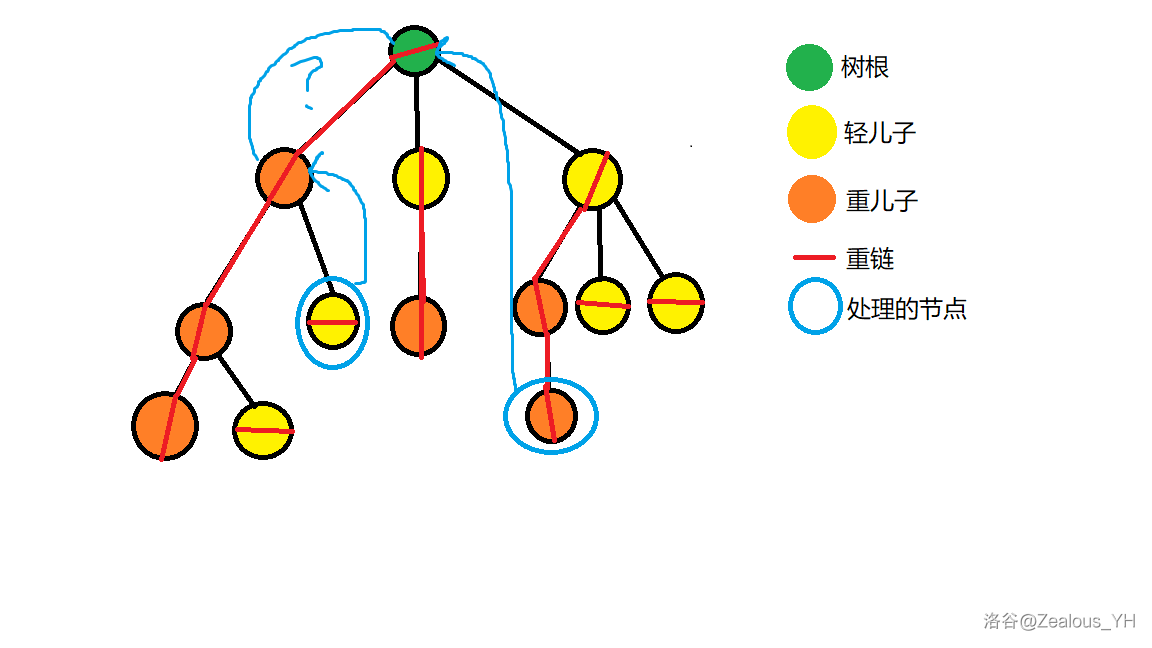
代码的话也很好写(如果不算线段树的话):
```
int querylink(int x,int y){
int ans=0;
while(tp[x]!=tp[y]){//不在同一链
if(dep[tp[x]]<dep[tp[y]]){//把x改成链顶深度更深的节点
swap(x,y);
}
ans+=query(1,1,n,id[tp[x]],id[x]);//加上x所在这条链的答案
x=fa[top[x]];//x跳上去,换一条链继续算权值
}//下面就是在同一条链了
if(dep[x]>dep[y]){//让x深度更小,编号也就越小
swap(x,y);
}
ans+=query(1,1,n,id[x],id[y]);//把剩下的零碎部分给算了
return ans;
}
```
那么链修改也非常容易,直接把 `query` 都改成 `modify` 就行了,直接 Ctrl+C 啊。
链上操作的复杂度是 $O(\log_2n)$,这里的内容一开始有点问题。
$\rm upd:$ @Sword_K 说,一个点到根的路径上只会有 $\log n$ 条重链,也就是只会跳 $\log n$ 条轻边,证明很简单,每跳一次轻边,子树大小至少翻倍(似乎有点类似启发式合并捏)。所以这里的复杂度是一个 $\log$ 再乘线段树的 $\log$。
#### 子树和
观察到子树编号是连续的,如果子树根的节点编号为 $x$,那么显然子树内最大的编号就是 $x+sum_x-1$,$sum$ 是我们记录的子树大小。
于是代码非常简单:
```
int querysont(int x){
return query(1,1,n,id[x],id[x]+sum[x]-1);
}
```
子树修改也同样地把 `query` 换成 `modify` 即可。这里的复杂度只有线段树,所以是 $O(\log n)$ 的。
### 建树
不能忘记的部分,但是非常简单,毕竟我们已经在 DFS 中转移了权值。
```
void build(int p,int l,int r){//这都是普通线段树了
if(l==r){
t[p]=w[l];
return;
}
int m=(l+r)>>1;
build(p<<1,l,m);
build(p<<1|1,m+1,r);
pushup(p);
}
```
把上面的内容都结合一下,再搞一棵线段树就行了。
## 一些有趣的注意事项
- 可以转边权为点权,因此树剖可以做点权树,也可以做边权树,当然结合都可以。
- 修改单边权或者单点权其实就是线段树上单点修改,不要问出来
> @Zealous_YH:@Hooch 修改单边权怎么做啊?
- 记得建树,记得 `pushup`。
## 总结
> StayAlone:树链剖分实在太简单了,我相信你们这个上午就能切很多题。