Linear Algebra Done Right(缓更)
sanaka87
·
·
个人记录
学期结束了,简单记录下自己的一些思维成果(并不是)
(以下基本都是自己的做法)
取 $(1,0),(0,1)$ 带入平行四边形恒等式:
$$2||x||^2+2||y||^2=||x-y||^2+||x+y||^2$$
$$2||(1,0)||^2+2||(0,1)||^2=||(1,-1)||^2+||(1,1)||^2$$
$$4=2\cdot2^{\frac 2p},p=2$$
------------

分别取出 $||_2,||_1$ 运算对应的标准正交基 $\{\alpha_1,\cdots,\alpha_n\},\{\beta_i,,\cdots,\beta_n\}$,然后对应的变换矩阵设为 $T$,就是:
$$(\beta_1 ,\cdots,\beta_n )T=(\alpha_1 ,\cdots,\alpha_n )$$
$$\alpha_i=\sum_{k=1}^n\beta_kT_{k,i}$$
设
$$v=\sum_{i=1}^nx_i\alpha_i=\sum_{i=1}^nx_i\sum_{k=1}^n\beta_kT_{k,i}=\sum_{k=1}^n\beta_k\sum_{i=1}^nx_iT_{k,i}$$
$$||v||^2_2=\sum_{i=1}^n|x_i|^2,||v||^2_1=\sum_{k=1}^n|\sum_{i=1}^nx_iT_{k,i}|^2$$
注意这些都可能是复数。根据复数的柯西不等式:
> $$(\sum_{i=1}^n|a_i|^2)(\sum_{j=1}^n|b_j|^2)\ge|\sum_{i=1}^na_ib_i|^2$$
$$||v||^2_1\le\sum_{k=1}^n(\sum_{i=1}^n|x_i|^2)(\sum_{j=1}^n|T_{k,j}|^2)$$
$$=(\sum_{i=1}^n|x_i|^2)\sum_{k=1}^n\sum_{j=1}^n|T_{k,j}|^2$$
$$=||v||^2_2\sum_{k=1}^n\sum_{j=1}^n|T_{k,j}|^2$$
右边这个就是我们要的 $c,c=\sqrt{\sum_{k=1}^n\sum_{j=1}^n|T_{k,j}|^2}$。
事实上这是一个正交矩阵(等距算子),满足 $TT^T=E$,这里是共轭转置。所以 $n=\sum_{i=1}^nE_{i,i}=\sum_{i=1}^n\sum_{j=1}^nT_{i,j}\overline{T}_{i,j}$。这题可以进一步加强证明 $c$ 可以取 $\frac{1}{\sqrt n}$。
------------
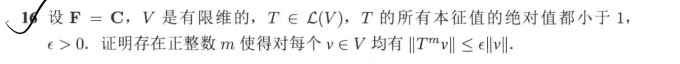
可以 Jordan 标准型。但是感觉有点杀鸡用牛刀。
还是先用套路,根据舒尔定理,取一个规范正交基 $\{a_i\}$ 使得 $T$ 在它下是上三角矩阵。那么设 $v=\sum_{i=1}^nx_ia_i,||Tv||=||\sum_{i=1}^nx_iT(a_i)||
=||\sum_{i=1}^nx_i\sum_{j=1}^na_jT_{j,i}||
=||\sum_{j=1}^na_j\sum_{i=1}^nx_iT_{j,i}||
=\sum_{j=1}^n|\sum_{i=1}^nx_iT_{j,i}|^2
同样用柯西不等式:
\le||v||\sum_{i=1}^n\sum_{j=1}^n|T_{j,i}|^2
那么问题其实变成证明 \lim\limits_{m\to\infty}T^m=0。我们现在来证明这个结论。
下证:
\lim_{m\to\infty}|T^m_{i,j}|=0
考虑数学归纳法,当 j-i=0 ,因为特征值绝对值 <1,显然成立。
不妨设 j-i\le k-2,k\ge2 ,成立,归纳证明 j-i=k-1 成立,不妨设 j=k,i=1:
T_{1,k}^{m+1}=\sum_{i=1}^kT^{m}_{1,i}T_{i,k}
\forall \varepsilon>0$ 根据归纳假设,对于每一个 $i$ 都有 $M_i,$ 使得 $m>M_i\Rightarrow T_{1,i}^m<\frac\varepsilon{nT_{i,k}}
取 M=\max\{M_1,\cdots,M_k\},m>M\Rightarrow T_{1,k}^{m+1}<\varepsilon。得证。
一类题(前提是有限维):
设 P\in L(V) 使得 P^2=P,存在一个子空间 U 使得 P=P_U 等价于:
我们证明一个普适性的结论:
命题:这等价于证明 (\text{range}P)^{\bot}=\text{null}P。
左推右:显然 \text{range}P=\text{range}P_U=U,根据投影变换的性质有 \text{null}P_U=U^{\bot},证毕。
右推左:我们证明 U=\text{range}P 可行。因为 (\text{range}P)^{\bot}=\text{null}P,那么投影变换可以写成:对于任意属于 V 的向量(根据直和的性质可以写成)u+v 满足 P_U(u+v)=u(u\in \text{range}P,v\in \text{null}P),而 P(u+v)=P(u)+P(v)=P(u),进一步发现,如果设 u=P(u'),P(u)=P^2(u')=P(u')=u,那么就有 P(u)=u。所以对比发现 P=P_U。证毕。
我们用这个普适性的结论解决上面的两道题。先看第一题。
题干条件相当于 $||P(u+v)||=||u||\le ||u+v||(u\in \text{range}P,v\in \text{null}P)$,那么如果 $\langle u,v\rangle \ne 0$,这其实是一个很强而且直观的条件,通过**正交分解**找到高线,取 $v'=-\frac{\langle u,v\rangle}{||v||^2}v$,就有 $||u+v'||=\sqrt{||u||^2-||v'||^2}<||u||$,矛盾!所以就证明了是子空间正交。
其实这也是一个有趣的命题:
> **命题**:$U^\bot=V\Leftrightarrow \forall u\in U,v\in V,||u||\le ||u+v||$。
左推右显然,右推左刚才证明了。
$(\text{range}P)^{\bot}=\text{null}P\Rightarrow ||Pv||\le||v||$:那其实就是显然的命题的另一边。
再看第二题。
$P$ 是自伴的 $\Leftrightarrow$ $(\text{range}P)^{\bot}=\text{null}P$,左推右比较显然,写一下右推左:对于任意 $u,v\in V$,根据直和分解 $u=u_x+u_y,v=v_x+v_y$,$x$ 属于 $\text{range}$,$y$ 属于 $\text{null}$(懒了),那么 $\langle Tu,v\rangle=\langle T(u_x+u_y),v_x+v_y\rangle=\langle u_x,v_x+v_y\rangle=\langle u_x,v_x\rangle=\langle u_x+u_y,v_x\rangle=\langle u,Tv\rangle$。证毕。
------------
关于伴随的证明问题:
如果只按照较为具象的“共轭转置”来证明伴随算子的问题显然是不够的,我们必须要从定义来。先看看课本对伴随、自伴、正规的一些推导。

很抽象的技巧:**一个向量是零向量等价于和空间里所有向量的内积都是 $0$。** 这就构造出了内积。

证明一个数是实数只需要证明这个数的共轭等于本身。所以两边同时乘上向量的模平方,再把模平方变成内积,把特征值扔进去,又构造出了内积。

同样的,证明实数等价于它减去共轭等于 $0$,然后再用第一个技巧结论。
这个结论特别经典,因为它告诉我们**复数域下的正算子一定是自伴的**。

第一个证明简单,因为正规的最基本性质其实是 $||Tv||=||T^*v||$,直接对特征值定义式做伴随。
第二个证明就有点逆天了。首先拿出正交的定义,通过左右两边同时乘上 $(\alpha-\beta)$ 来用上特征值的条件,再利用新鲜出炉的结论(就是上一条)推导出所需要的等式。
看了半天发现就是**构造内积**。然后看看习题:
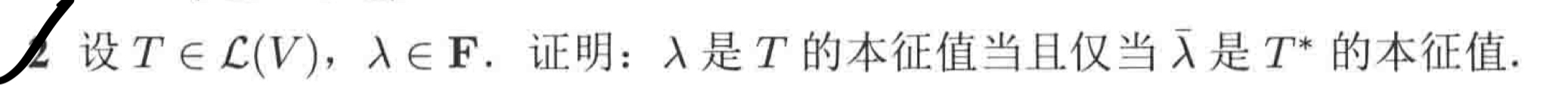
这个结论还挺强的,课本上居然没直接给出...当时睡前一直想不出来,一觉醒来就会了(这是第二题啊 orz)...
首先显然只需要左推右,因为共轭两次就是自己,伴随两次也是自己。对于任意的 $w$ 和特征向量 $v$ 构造内积:
$$\langle(\lambda I-T) v,w\rangle=0$$
$$\langle v,(\overline{\lambda} I-T^*)w\rangle=0$$
如果没有非零的 $w$ 使得 $(\overline{\lambda} I-T^*)w=0$,那么 $(\overline{\lambda} I-T^*)$ 就是一个单射,此时一定存在 $(\overline{\lambda} I-T^*)w=v$,带入式子发现 $||v||=0$,和特征向量定义矛盾!所以证毕。

构造内积,$U$ 在 $T$ 下不变 $\Leftrightarrow\ \langle Tu,v\rangle=0$ 对任意 $u\in U,v\in U^\bot$ 成立 $\Leftrightarrow\ \langle T^*v,u\rangle=0$ 对任意 $u\in U,v\in U^\bot$ 成立 $\Leftrightarrow\ U^\bot$ 在 $T^*$ 下不变。

室友问我的题,首先这个肯定是错的,条件太弱了,思考一下怎么构造。条件相当于 $\langle e_j,(TT^*-T^*T)e_j\rangle=0$,考虑最简单的 $R^2$ 和内积。
$$T=\begin{pmatrix}
a & b\\
c & d
\end{pmatrix}$$
$$TT^*=\begin{pmatrix}
a & b\\
c & d
\end{pmatrix}\begin{pmatrix}
a & c\\
b & d
\end{pmatrix}=\begin{pmatrix}
a^2+b^2 & ac+bd\\
ac+bd & c^2+d^2
\end{pmatrix}$$
$$T^*T=\begin{pmatrix}
a & c\\
b & d
\end{pmatrix}\begin{pmatrix}
a & b\\
c & d
\end{pmatrix}=\begin{pmatrix}
a^2+c^2 & ab+cd\\
ab+cd & b^2+d^2
\end{pmatrix}$$
$$TT^*-T^*T=\begin{pmatrix}
a & c\\
b & d
\end{pmatrix}\begin{pmatrix}
a & b\\
c & d
\end{pmatrix}=\begin{pmatrix}
b^2-c^2 & (a-d)(c-b)\\
(a-d)(c-b) & c^2-b^2
\end{pmatrix}$$
根据题干条件,$b^2=c^2$,但是可以一正一负,不妨设 $b=1,c=-1$,那么:
$$TT^*-T^*T=\begin{pmatrix}
a & c\\
b & d
\end{pmatrix}\begin{pmatrix}
a & b\\
c & d
\end{pmatrix}=\begin{pmatrix}
0 & -2(a-d)\\
-2(a-d) & 0
\end{pmatrix}$$
再设 $a=1,d=0$,那么原矩阵 $T=\begin{pmatrix}1 & 1\\
-1 & 0\end{pmatrix}$,这就是一个满足条件的反例。

最简单且最基本的性质,只不过要注意还要证明它是自伴的。

这又把条件弱化了,考虑怎么找到反例。我的想法是通过构造 $\langle Te_j,e_j\rangle=0$,但又不是正的,这就比较简单,我让 $(1,0)\to(0,-2),(0,1)\to(1,0),\therefore (1,1)\to(1,-2),\langle(1,1),(1,-2)\rangle=-1<0$。
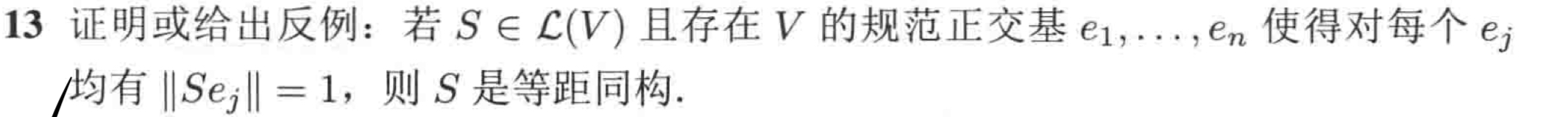
又是弱化条件,但是这个就很水了,我直接把 $(1,0),(0,1)$ 都送到 $(1,0)$ 就好,但是显然这不是等距同构...因为甚至不可逆。
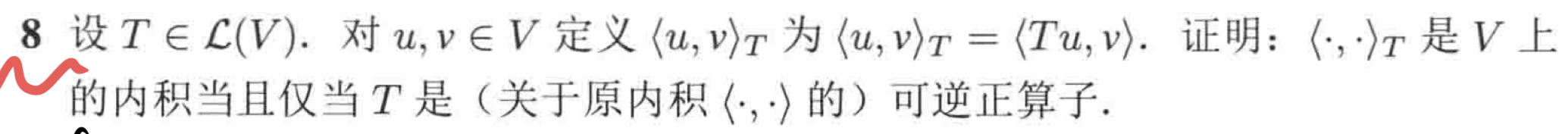
助教补充题。
左边推右边:先证明自伴,所以我们要构造内积,可以直接用**内积的性质**, $\langle u,v\rangle_T=\overline{\langle v,u\rangle}_T=\langle Tu,v\rangle=\langle u,Tv\rangle$,所以它自伴。然后我们还要证明 $\langle u,u\rangle_T=\langle Tu,u\rangle\ge 0$,我们证明了 $T$ 是正的。接下来还要说它可逆?因为这是关于算子的书不要考虑矩阵的事情,我们**证明 $T$ 是一个双射**,出发空间和到达空间相同,所以只需要证明是单射,也就是证明 $Tv=0\Rightarrow v=0$。套路化的,前面的条件等价于 $\langle Tv,w\rangle$ 对 $w\in V$ 恒成立,$\langle v,w\rangle_T$ 对 $w\in V$ 恒成立,那么显然 $v=0$。证毕。
右边推左边就需要证明五条性质。

正性根据 $T$ 是正的显然。
定性:$\langle Tu,u\rangle=0$ 如何推出 $u=0$?直接做肯定不行,用上正的结论。因为 $T$ 是正的,所以可以分解成 $T=R^*R$(重要结论!当然你用正的平方根也可以),所以 $\langle Ru,Ru\rangle=0$,$Ru=0,R^*Ru=Tu=0$,因为可逆,所以 $u=0$。
第一个位置的加性和齐性根据线性映射的性质和内积性质直接得出。
共轭对称性也是根据自伴直接得出。
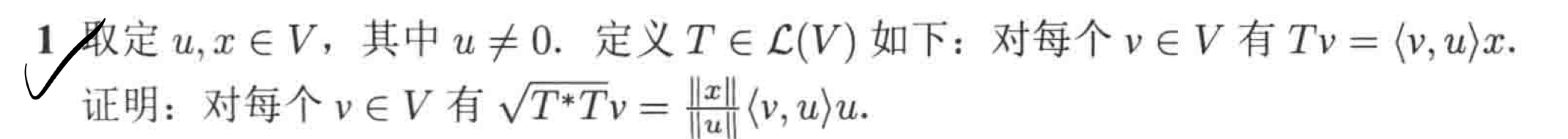
这个直接开根号根本不会,然后 $T^*$ 也不会求,怎么办呢?还是构造内积。
首先我们求 $T^*T$。怎么构造?
我的方法:取出一组规范正交基 $\{e_i\}$,根据经典性质有:
$$T^*T(v)=\sum_{i=1}^n\langle T^*T(v),e_i\rangle e_i$$
$$=\sum_{i=1}^n\langle T(v),T(e_i)\rangle e_i$$
$$=\sum_{i=1}^n\langle \langle v,u\rangle x,\langle e_i,u\rangle x\rangle e_i$$
$$=\sum_{i=1}^n\langle v,u\rangle \langle u,e_i\rangle ||x||^2 e_i$$
$$=||x||^2\langle v,u\rangle u$$
接下来其实只需要证明 $R(v)=\frac{||x||}{||u||}\langle v,u\rangle u$ 是平方根,只需要证明:
- $R^2(v)=||x||^2\langle v,u\rangle u$ 对任意 $u\in V$ 都成立。
这个带进去,
$$R(R(u))=R(\frac{||x||}{||u||}\langle v,u\rangle u)=\frac{||x||}{||u||}\langle \frac{||x||}{||u||}\langle v,u\rangle u,u\rangle u$$
(逆天)
$$={||x||^2}\langle v,u\rangle u$$
- $R$ 是正的。
先证明自伴,
$$\langle R(a),b\rangle=\langle\frac{||x||}{||u||}\langle a,u\rangle u,b\rangle=\frac{||x||}{||u||}\langle a,u\rangle \langle u,b\rangle$$
凑出一个内积:
$$=\langle a,\frac{||x||}{||u||}\langle b,u\rangle u\rangle =\langle a,R(b)\rangle$$
然后 $\langle R(a),a\rangle=\langle\frac{||x||}{||u||}\langle a,u\rangle u,a\rangle=\frac{||x||}{||u||}|\langle a,u\rangle u|^2\ge 0
所以证毕了。
极分解和奇异值分解咕了。这是人学的?
关于广义特征向量空间和对角化的一些题目。
只要记住一个经典不可对角化矩阵 \begin{pmatrix}1&1\\0&1\end{pmatrix},平方一下 \begin{pmatrix}1&2\\0&1\end{pmatrix} 还是不可对角化的。
发现二阶找不到反例,然后复空间肯定是对的(因为根据舒尔定理它就是一个对角线全是 0 的上三角矩阵!)。所以一个基本的想法就是,构造一个 0 为一重特征值,两个共轭复数作为二重特征值,那么这个算子只有一个特征值 0 了,因为是实向量空间。
\begin{pmatrix}0&0&1\\0&0&0\\-1&0&0\end{pmatrix}
特征多项式 \lambda(\lambda^2+1)。
助教的做法:首先根据题目条件有 \dim\text{null}T^{n-1}\ge n-1,那么如果维数是 n,那么整个矩阵幂零,特征值只能是 0。如果是 n-1,取出核空间的基,那么在这个基下是幂零矩阵,扩张这组基,矩阵多了一行一列,那么得到一个对角线上全是 0,最后一个元素不确定的上三角矩阵,特征值最多两个。
我的做法有点低能...抽屉原理,还证明了一个引理,不写了。
很经典而且很实用的性质,但是真的不会证 orz。明天早上起来补。
其实我们发现,只需要证明 v\in\text{null}(\lambda I-T)^n\Rightarrow v\in\text{null}(\lambda^{-1} I-T^{-1})^n。瓶颈在于这个 n 我们无法处理,总不可能二项式展开。所以我们对 n 使用数学归纳法。
当 n=1 的时候,Tv=\lambda v,\therefore v=\lambda T^{-1}v,T^{-1}v=\lambda^{-1}v。
不妨设 n=k-1 的时候成立 (k\ge 2),那么对于 v\in\text{null}(\lambda I-T)^n,(\lambda I-T)^{n-1}((\lambda I-T)v)=0, 根据归纳假设 ((\lambda^{-1}I-T^{-1})^{n-1}(\lambda I-T))v=0。如果能交换一下顺序那么就做完了!其实有一个经典的引理:
命题:若 AB=BA,那么 对于多项式 P,Q\in R[x],P(A)Q(B)=Q(B)P(A)。
证明其实很显然,直接拆了用条件即可。
因为 T,T^{-1} 显然可交换,那么就有 (\lambda I-T)((\lambda^{-1}I-T^{-1})^{n-1}v)=0,又因为 n=1 成立就有 (\lambda^{-1} I-T^{-1})^nv=0。证毕。
关于极小多项式。
我们考察下面几个矩阵的极小多项式:
显然极小多项式 s(x)=(x-\lambda)。
特征多项式是 p(x)=(x-\lambda)^n,那么极小多项式 m(x) 一定是 (x-\lambda)^s(s\in[1,n]) 的形式。显然 T-\lambda E 没乘上自己一次相当于就是对角线向上平移,所以 s=n,极小多项式只能是 m(x)=p(x)=(x-\lambda)^n。
所以一个线性变换的极小多项式可以直接从 Jordan 块里看出,对应特征值 \lambda 的多项式次数就是 Jordan 块最大的大小。
尝试用这个结论薄纱这题。首先左推右简单,直接对特征空间做直和分解,每一项都可以找到相应的特征子空间然后代入多项式,得到等于 0。
右推左的话就用这个结论,没有重复的零点,所以 Jordan 标准型中所有的 Jordan 块大小都是 1,那么就是对角矩阵了,显然证毕。
一个思路。