算法总结——进阶前缀和2
program_xwl
·
·
算法·理论
前缀和主要用于求解静态区间求和,这篇文章会讲解更难一些的前缀和问题。
例题1 [USACO16JAN] Subsequences Summing to Sevens S
看到区间求和,就可以想到前缀和。
思路:
先复习一下魔(模)法公式:\
$(a\times b) \mod c = (a\mod c\times b\mod c)\mod c$\
(注意没有减法和除法)\
\
设 $sum_i$ 表示数组前 $i$ 项之和,那么问题就变成了:在 $R-L$ 尽量大的情况下, $(sum_R-sum_{l-1})\mod 7 =0$ 。\
\
如果 $x\mod 7 = x_m,x/7=x_d$。
那么:\
$x = 7x_d+x_m$\
如果 $x = a_m=b_m$\
那么:\
$a-b = 7a_d+a_m-7b_d-b_m=7(a_d-b_d)+a_m-b_m = 7(a_d-b_d){\color{Red}+x-x} = 7(a_d-b_d)$\
可以发现,余数抵消了,这就是同余原理,也是解这题的关键。这意味着什么呢?我们只需要找到两个距离最长的,前缀和模上 $7$ 相等的两个前下标 $L,R$ ,区间 $[L+1,R]$ 就是合法的。有了上一句的结论,我们就只要遍历一遍,找到下模 $7$ 的每一种情况首次出现和最后一次出现是在那个位置,再遍历所有情况,找到首次出现和最后一次出现跨度最大的情况。特别注意 $0$ 的情况,它的第一次出现应该是在下标为 $0$ 因为可以把元素前面的全部选中合成一个区间。
### 代码:
```cpp
#include <bits/stdc++.h>
using namespace std;
int n,a[50005],sum[50005],st[15],ed[15];
int main(void)
{
cin >> n;
for(int i = 1;i <= n;i++)
{
cin >> a[i];
a[i] %= 7;
sum[i] = sum[i-1] + a[i];
sum[i] %= 7;
}
for(int i = 1;i <= 6;i++) st[i] = -1;
st[0] = 0;
for(int i = 1;i <= n;i++)
{
if(st[sum[i]] == -1) st[sum[i]] = i;
ed[sum[i]] = i;
}
int maxi = 0;
for(int i = 0;i < 7;i++) maxi = max(maxi,ed[i]-st[i]);
cout << maxi;
return 0;
}
```
## 例题2 [[蓝桥杯 2017 省 B] k 倍区间](https://www.luogu.com.cn/problem/P8649)
它可以说是例题1改出来的。
### 思路:
它肯定不能只记下一种余数第一次出现的和最后一次出现的,它需要求合法的方案数。在这题中,我们需要统计每种余数出现的个数,来计算配对的方案数。但这个方案数有个坑,设有 $4$ 个点的前缀和模 $k$ 的结果相同,这些点分别用 $d1,d2,d3,d4$ 来表示,则配对情况如下图。
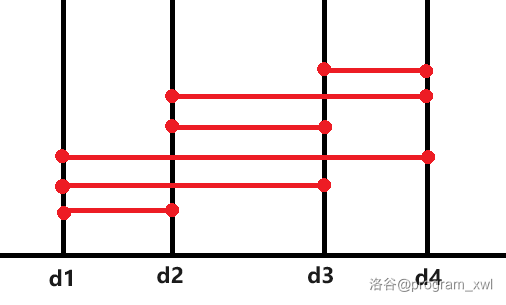
在题目中 $i$ 可以等于 $j$ ,那是在 $A$ 序列中,在前缀和数组中不行,因为那样相当于什么也没有,设点数为 $x$ ,那么公式是:
$$
\cfrac{x(x-1)}{2}
$$
我们只需要在最后遍历所有前缀和中各个余数的可能,按照上面的公式一并累加即可:\
$cnt_i$ 表示余数 $i$ 出现的次数
$$
ans = \sum _{i=0}^{i=k-1} \cfrac{cnt_i\times(cnt_i-1)}{2}
$$
### 代码:
```cpp
#include <bits/stdc++.h>
using namespace std;
long long n,k,sum[100005],cnt[100005],ans = 0;
int main(void)
{
cin >> n >> k;
cnt[0] = 1;
for(int i = 1;i <= n;i++)
{
int x;
cin >> x;
x %= k;
sum[i] = (sum[i-1] + x) % k;
cnt[sum[i]]++;
}
for(int i = 0;i < k;i++) ans += cnt[i]*(cnt[i]-1)/2;
cout << ans;
return 0;
}
```
## 例题3 [Number of Ways](https://www.luogu.com.cn/problem/CF466C)
### 思路
既然要将序列两分为三,还需要分成的三份的元素之和相等,那么很容易看出有借情况下每份的总和必定等于序列元素总和的三分之一,如果序列元素总和不是三的倍数或是序列长度不足 $3$ 直接输出 $0$ 结束。\
设序列元素总和的三分之一为 $acsum$ ,前缀和数组为 $sum$\
通过上面的结论我们知道合法的子串 $[1,i]$ 的元素总和必定是 $acsum$ , $sum_i$ 的前缀和也是 $acsum$ ;而合法的子串 $[i+1,j]$ 也是 $acsum$ , $sum_j$ 而前缀和是 $sum_i+acsum$ 也就是序列元素总和的三分之二。\
我们只需要枚举所有位置,通过前缀和数组判断该位置是否可以是 $i$ 或 $j$ ,由于它们的判断条件不同,所以不能用一个计数器存储。可以用一个 $cnt$ 存储到该位置有多少个可行的 $i$ 位置,只要发现一个可行的 $j$ 位置,就把总和计数器加上**之前**所有可行的 $i$ 位置数量,最后答案就是总和计数器的值。
### 代码:
```cpp
#include <bits/stdc++.h>
using namespace std;
long long n,a[500005],sum[500005],ac_sum;
int main(void)
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> n;
for(int i = 1;i <= n;i++)
{
cin >> a[i];
sum[i] = sum[i-1] + a[i];
}
if(sum[n] % 3 != 0 || n <= 2)
{
cout << "0\n";
return 0;
}
ac_sum = sum[n] / 3;
long long ans = 0,cnt = 0;
for(int i = 1;i <= n;i++)
{
if(i > 1 && i < n && sum[i] == ac_sum*2) ans += cnt;
if(sum[i] == ac_sum) cnt++;
}
cout << ans;
return 0;
}
```