握手 题解

开学了，高一(21)班共有$n (n\in \mathbb{N^{*}})$名同学，他们的学号分别是$1,2,\cdots,n$。班主任为了让同学们相互认识，想了一个好办法。 他在一次班会课上说：“同学们，如果你的学号是$x$，而另一个同学的学号是$y$，并且$x+y=2^{k}+2(k\in \mathbb{N})$，那么你们之间就有缘分。现在请你和所有与你有缘分的同学握手吧！” (1) 当$n=30$时，求所有与$5$号同学握手的同学的学号。 (2) 求同学们握手的总次数。 (3) 班主任的办法很有效，握过手的两名同学**互相**成为了朋友。而且这种朋友关系还具有传递性，即如果甲、乙是朋友，乙、丙是朋友，那么甲、丙也是朋友。现在21班要组建一个团队参加比赛，为了保证团队的团结，要求团队中任意两人都是朋友。求团队中人数的最大值。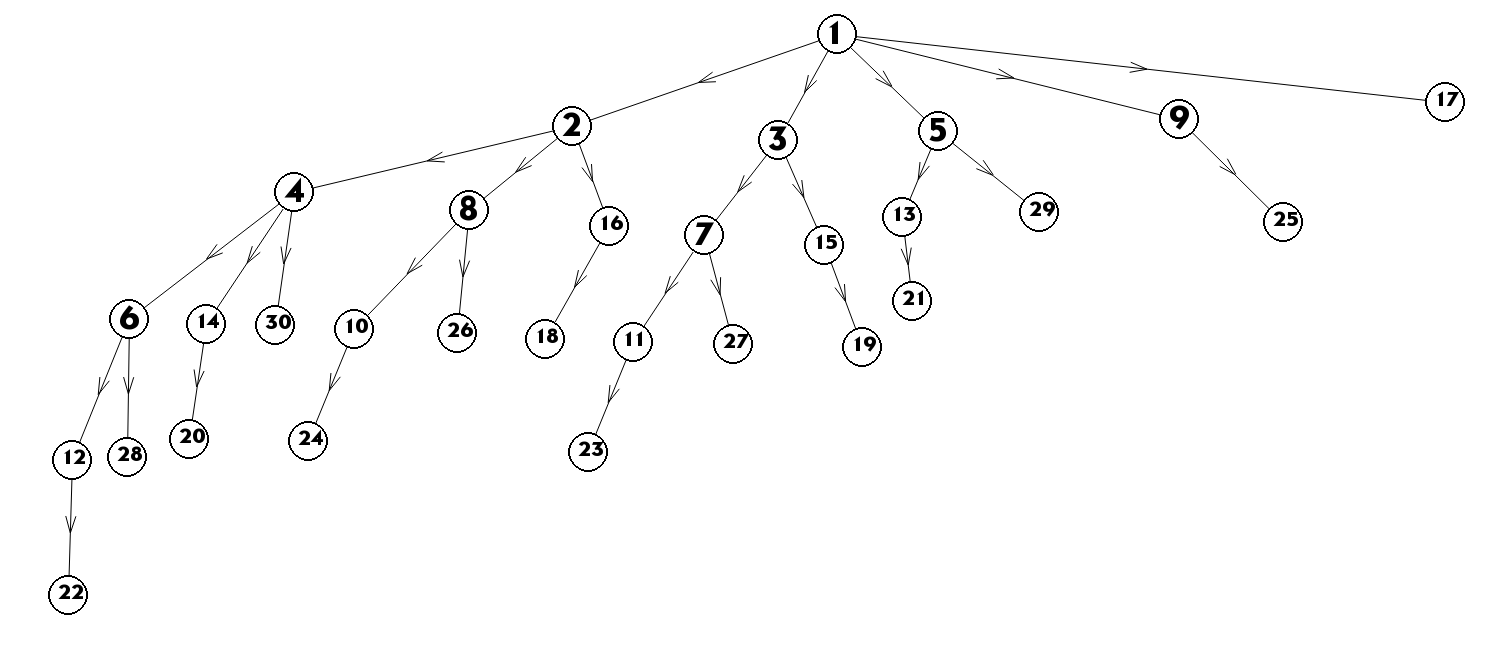 --- 题解： (1) $n=30$时，握手关系如下图：  因此所有与$5$号同学握手的同学的学号所组成的集合为$\left \{ 1,13,29 \right\}$。 --- (2) 把$1$号同学称为“根”~~（可以理解为“全班的希望”）~~。 设$x$为集合$A=\left \{ x\in \mathbb{N} \mid 1<x\le n \right\}$中的任意元素。对于某一个$x$，设$y$是集合$\left \{ y\in \mathbb{N} \mid 1\le y< x \right\}$中的某个元素，且有$x+y=2^{k}+2(k\in \mathbb{N})$。如果存在这样的$y$，那么我们称$y$为$x$的“父亲”~~（$\sout{x}$被$\sout{y}$打败了，被迫承认的）~~。 下面我们证明，对于$A$中的每一个元素，都有且仅有$1$个父亲~~（废话，你还能认两个人作父亲？）~~。 整数$y$是$x$的父亲当且仅当$0<y<x$且$x+y=2^k+2$。 上述条件成立，当且仅当存在一个自然数$k$，使得$0<2^k+2-x<x$。调整得到$x<2^k+2<2x$，即$x-2<2^k<2x-2$。 下面证明对于每一个$x$，有且只有一个自然数$k$满足上式。 设$$x-2=2^{a_1}+2^{a_2}+\cdots+2^{a_n}$$ 其中 $a_1>a_2>\cdots>a_n,\left\{a_1,a_2,\cdots,a_n\right\}\subseteq \mathbb{N}$。 则$$x-2=2^{a_1}+2^{a_2}+\cdots+2^{a_n}\le 2^{a_1}+2^{a_1-1}+2^{a_1-2}+\cdots+2^{1}+2^{0}<2^{a_1+1}$$ 而$2x-4=2(x-2)=2^{a_1+1}+2^{a_2+1}+\cdots+2^{a_n+1}\ge 2^{a_1+1}$。 于是$x-2<2^{a_1+1}\le 2x-4$，知$x-2<2^{a_1+1}<2x-2$，知存在$k=a_1+1$使得上式成立。 再证明$a_1+1$是唯一满足条件的$k$。 若有$k'<a_1+1$满足上式，那么由$k'\in \mathbb{N}$知$k'\le a_1$，则$2^{k'}\le 2^{a_1}\le x-2=2^{a_1}+2^{a_2}+\cdots+2^{a_n}$，与上式矛盾。 若有$k'>a_1+1$满足上式，那么由$k'\in \mathbb{N}$知$k'\ge a_1+2$，则$2^{k'}\ge 2^{a_1+2}>2^{a_1+1}+2^{a_1}+2^{a_1-1}+\cdots+2^1+2^0$。 而$2x-4=2^{a_1+1}+2^{a_2+1}+\cdots+2^{a_n+1}<2^{a_1+1}+2^{a_1}+2^{a_1-1}+\cdots+2^1+2^0$（此处请注意：因为$a_1>a_2>\cdots>a_n\ge0$，所以$a_1+1>a_2+1>\cdots>a_n+1\ge1$。） 于是有$2^{k'}>2x-4$。 然而，若$x-2<2^{k'} <2x-2$，则有$2^{k'}<2x-2$，由$2^{k'}\in \mathbb{N}$知$2^{k'}=2x-3$；而由于$k'>a_1+1\ge1$，知$2^{k'}$一定是偶数，出现矛盾。 综上，$a_1+1$是唯一满足条件的$k$。 由此，我们得出，对于$A$中的每一个元素，都有且仅有$1$个父亲。 考虑每一次握手，设握手的两人分别为$x$和$y$，不妨设$x>y$，则由上面的结论知$y$是$x$的父亲，因此每一次握手都仅在一个人和他的父亲之间发生~~（“发生”这个词好恐怖）~~，且学号大于$1$的每个人都会和他的父亲握手。 有多少对父子关系就有多少次握手。$1$没有父亲，而所有学号大于$1$的人都有父亲，因此同学们握手的总次数为$n-1$。 --- (3) 我们设$1$的祖先为$1$本身~~（我 生 我 自 己）~~，其余点的祖先定义为它父亲的祖先。（可以看上面的图帮助理解，按照图上的箭头反向往上走，走到最上面就是祖先。也可以理解为祖先是父亲的父亲的父亲的……父亲的父亲。） 用符号语言来表示，记一个人的父亲为$\text{par}(x)$，记一个人的祖先为$\text{gpar}(x)$。那么若$x=1$，则$\text{gpar}(x)=1$；否则$\text{gpar}(x)=\text{gpar}(\text{par}(x))$。如$\text{gpar}(2)=\text{gpar}(\text{par}(2))=\text{gpar}(1)=1$。 由父亲和祖先的定义知，一个人和他的祖先一定有朋友关系~~（怎么看着怪怪的）~~。 观察上面的图，我们发现图上每一个人的祖先都是$1$！这是不是巧合呢？ 事实上，我们可以证明，任意满足$1\le x\le n$的整数的祖先都是$1$。 怎么证明呢？我们可以 ~~感性理解~~ 用数学归纳法。 首先，当$x=1$时，按照定义，欲证命题显然成立。 接着，我们设当$x\le k$时欲证命题成立，即“任意满足$1\le x\le k$的整数的祖先都是$1$”成立。下面我们要证明当$x=k+1$时命题也成立。 由(2)，$\text{par}(k+1)<k+1$，由于$\text{par}(k+1)\in \mathbb{N}$，知$\text{par}(k+1)\le k$，由归纳假设知$\text{gpar}(\text{par}(k+1))=1$。由祖先的定义知$\text{gpar}(k+1)=1$，即欲证命题在$x=k+1$时也成立。 根据数学归纳法，对任意满足$1\le x\le n$的整数，$\text{gpar}(x)=1$。 （由于我们还没有学过数学归纳法，因此这段证明过程在实际书写时可以略微 ~~意会~~ 调整。） 于是，每一个人都和$1$号同学是朋友。由朋友关系的传递性，全班同学都彼此是朋友。因此团队中人数的最大值为$n$。 --- 这道题解完了，我们有什么收获呢？ 我们要向高一(21)班的同学学习，让我们的班集体变得更团结~~，变得更团结的方式就是彼此认父亲，并发生握手关系~~。 --- 好了好了，言归正传。 “父亲”其实是图论中的一个重要概念。上面的图片是图论中“树”的模型，相信有些同学也听胡冬明老师讲过“最小生成树”，那里的“树”和这里的“树”是同一个概念。 图论是数学和计算机科学重要的研究对象，大家小学时做的“一笔画问题”就是图论知识的一个应用，这个问题是欧拉最先解决的，欧拉被誉为图论之父。 如果大家学习数学竞赛（$\text{MO}$）或者信息学竞赛（$\text{OI}$），就一定会接触到许多关于图论的有趣内容。欢迎大家来学$\text{MO}$和$\text{OI}$呀~ （尤其安利~~没有多少人学的~~$\text{OI}$） 这篇文章发布在[洛谷](https://www.luogu.org)上。洛谷是一个$\text{OI}$学习网站，来洛谷看看，你就能领略到$\text{OI}$的魅力！$\text{OIer}$们都是很有趣又很友善的人呢！