ACL Contest 1 题解
Froggy
·
·
个人记录
ACL Contest 1
感觉题目挺好玩的就来补一下题解。
A - Reachable Towns
先把点按 x_i 从小到大排序,然后一个一个扫过去。
有个显然的 \mathcal{O}(n^2) 暴力连边做法,不过由于我们只需要求每个联通块的大小,所以很多边都是无用的。
考虑维护一个单调栈,栈里面每个点都满足它的 y_j 是它所属联通块中所有 y_j 的最小值,且栈里面的点的 y_j (从栈底到栈顶)单调递减。
新加一个点 (x_i,y_i),那么弹出栈中所有满足 y_j<y_i 的点,然后将所有被弹出的点 j 都和 i 进行连边,最后把这个联通块中 y_j 最小的点在压进栈里即可。
显然这样做边数是 \mathcal{O}(n) 的。
时间复杂度:\mathcal{O}(n\log n)。
code
B - Sum is Multiple
转化一下题意:找到最小的 k,满足:2n\mid k(k+1)。
显然需要把 2n 质因数分解掉。假设 2n=p_1^{q_1}\times\cdots\times p_m^{q_m},因为 \gcd(k,k+1)=1,所以对于每个 p_i^{q_i} 要么可以整除 k,要么可以整除 k+1。k 和 k+1 分别分配的数可以 2^m 进行枚举。
假设分配的数的积分别是 x 和 y,那么现在的目标就是找到一个最小的 k,满足 x\mid k 且 y\mid (k+1),转化为同余方程后可以拿 exgcd 直接解决。
或者直接用 Atcoder Library 里面的 excrt 也行。
时间复杂度:\mathcal{O}(2^m\log n)。拿计算器算一算会发现 m 的最大值是 13。
code
C - Moving Pieces
比较裸的一道网络流。
有个显然的建图方法:
如果 $(i,j)$ 为 `o`,那就再连一条 $S\rightarrow(i,j)$ 的一条流量为 $1$,费用为 $0$ 的边。
不过这样建图跑最小费用最大流需要用自己的板子,因为 Atcoder Library 里面使用 Dijkstra 实现的,有负边就会 GG。
那么不妨修改一下,$(i,j)\rightarrow T$ 连的费用改成 $n+m-i-j$,然后 $(i,j)\rightarrow(i+1,j)$ 和 $(i,j)\rightarrow(i,j+1)$ 的费用改成 $0$,每个 $(i,j)$ 为 `o` 的点都先把答案加上 $n+m-i-j$,最后减掉流的最小费用即可。
可以这样理解:如果一个点从 $(i,j)$ 走到了 $(i',j')$,那么它走的距离就是 $(i'+j')-(i+j)$。
时间复杂度:$\mathcal{O}(\mathrm{Flow}(n+m,n+m))$。
[***code***](https://atcoder.jp/contests/acl1/submissions/17077437)
---
### [D - Keep Distances](https://atcoder.jp/contests/acl1/tasks/acl1_d)
先考虑怎么求每次询问的区间中合法点集的大小的最大值。
假设求出了每个位置 $i$ 下一个距离 $\geq k$ 的位置 $nxt_i$,那么就可以用倍增轻松统计出从 $l_i$ 最多能跳多少次。
容易看出,第 $i$ 次在保证最终跳的次数最多的前提下能跳的范围其实是个区间。也就是说,如果最多能跳 $x$ 次,那么这次询问的答案就是这 $x$ 个区间的长度之和。
假设这 $x$ 个区间分别是 $(p_1,q_1),(p_2,q_2),\cdots,(p_x,q_x)$,那么答案就是 $x+\sum q_i-\sum p_i$。也就是说,我们分别求出 $\sum p_i$ 和 $\sum q_i$ 即可。
求左端点之和 $\sum p_i$ 就再弄了倍增数组记录,跳的时候就顺便加一加即可。
再思考一下会发现,区间右端点之和 $\sum q_i$ 其实就是从 $r_i$ 往前跳的所有 $x$ 个位置编号之和。也就是说需要找到每个位置 $i$ **上一个**距离 $\geq k$ 的位置 $pre_i$,类似于求 $\sum p_i$ 一样弄两个倍增数组即可。
时间复杂度:$\mathcal{O}((n+q)\log n)$。
[***code***](https://atcoder.jp/contests/acl1/submissions/17077188)
---
### [E - Shuffle Window](https://atcoder.jp/contests/acl1/tasks/acl1_e)
考虑对于一对 $(i,j)$ ($i<j$)它们交换过来的概率为多少。
先设一个函数 $f(i)=\max\{1,i-k+1\}$,表示位置 $i$ 最开始能被第 $f(i)$ 个区间覆盖到。
考虑某一时刻一个区间同时覆盖到了 $i$ 和 $j$,那么在这之后 $i$ 和 $j$ 交换过来的概率显然是 $\frac{1}{2}$。
考虑在这个时刻之前,有 $f(j)-f(i)$ 次只有 $i$ 被区间覆盖,这时 $i$ 每次被单独覆盖的时候 $i$ 有 $\frac{1}{k}$ 的概率被放到最左侧,那么以后就永远也覆盖不到它了。
令 $p=\frac{k-1}{k}$,通过刚才的分析容易知道,$i$ 和 $j$ 交换过来的概率就是 $\frac{p^{f(j)-f(i)}}{2}$。
根据期望的线性性,可以把每对 $(i,j)$ 的贡献分开来算。可以把 $p^{f(i)}$ 和 $p^{-p(j)}$ 分开来后根据乘法分配律用树状数组加速统计。
时间复杂度:$\mathcal{O}(n\log n)$。
[***code***](https://atcoder.jp/contests/acl1/submissions/17099922)
---
### [F - Center Rearranging](https://atcoder.jp/contests/acl1/tasks/acl1_f)
神仙题。
$B$ 中肯定最左边一段是 $A$ 通过放左边操作来的,这种数标记为 `L`,同理,最右边一段是 $A$ 通过放右边操作来的,这种数标记为 `R`,其它数标记为 `M`。
那么,标记后的序列 $B$ 就形如 `LLL...LLMM..MMRR..RRR`。可以先 $\mathcal{O}(n^2)$ 枚举 `L` 和 `M` 以及 `M` 和 `R` 的分界点。如果可行,那么最少的操作次数就是 $3n-cnt_M$ ($cnt_M$ 表示 `M` 的个数)了。
对于每种数的情况,可以分成 $3$ 大类。($A$ 中没有动用 `M` 表示,否则用 `.` 表示)
1.
```
A: M.. ...
B: LMR LLR
```
2.
```
A: ..M ...
B: LMR LRR
```
3.
```
A: M.. ..M MMM M.M M.M
B: MRR LLM MMM LMM MMR
```
容易发现,只有 `LMR` 的 `M` 的位置是没有确定的,其它情况都能确定。
如果一个 $B$ 中一个位置为 `M`,那就将它与它对应的 $A$ 中的位置连一条边,如果都连完后发现右边相交,就说明无解。
考虑如果 `LMR` 的情况都确定了,除此之外还需要再判断些什么。
对于第一二类,它们的操作顺序是有限制的:第一类第一步一定是 `push_back`,第二类的第一步一定是 `push_front`。
建一个有向图,图中每条边 $(u,v)$ 表示 $u$ 表示在 $v$ 之前操作。显然,这张图如果合法那么一定不存在环。
对于第一类,`R` 所在位置向 `L` 所在位置连边,对于第二类,`L` 所在位置向 `R` 所在位置连边。容易发现,此图有点特殊。设每种数三个在 $B$ 中位置分别是 $(x_i,y_i,z_i)$,那么图有环当且仅当存在一种第一类的数 $i$ 和第二类的数 $j$ 满足 $x_i>x_j$ 且 $z_i>z_j$。
如果出现了这种情况,环大概张这样: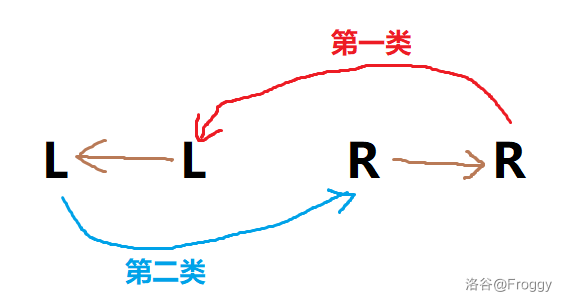
问题就转化为是否存在对每个 `LMR` 确定类型的一种合法方案。
容易发现之前说的所有限制都是二元限制,可以直接用 2-SAT 解决。
时间复杂度:$\mathcal{O}(n^4)$。
[***code***](https://atcoder.jp/contests/acl1/submissions/17202948)