单向连通图判定定理的证明
ipLee
·
·
个人记录
前言
在学习屈婉玲、耿素云、张立昂主编的《离散数学(第2版)》时,老师介绍P306页的定理14.9(课本上略去了其证明)时说其和定理14.8的证明很像,但是课上我没有想到到底怎么证,之后在复习时思考了该定理的证明,并且最终写出了证明方法,特此分享出来
(上为课本原文)
证明
目标
我们需要证明的是:对于有向图 D=<V,E>,D是单向连通图 当且仅当 D中存在经过每个顶点至少一次的通路
右推左很显然,我们这里证明左推右,也就是:对于有向图 D=<V,E>,D是单向连通图 可以推得 D中存在经过每个顶点至少一次的通路
在所有证明过程中会自动删去自环和平行边,因为它们显然不影响结论的正确性
符号和名词解释
- DAG:即Directed Acyclic Graph,中文是有向无环图,指一个没有圈的有向图,也就是这里的环实际上指的是圈(事实上百度“有向无圈图”会被定向到“有向无环图”)
-
-
u\to v$:$u$单向可达$v
-
-
-
引理
有下面几条引理,按编号为
-
DAG的子图一定是一个DAG
-
对于有向图D=<V,E>,若其为DAG,那么对于\forall w\in V,必然可以将除了w剩下的点集V-\{w\}划分成两个部分:U_w和V_w,其中\forall u\in U_w,u\to w、\forall v\in V_w,w\to v,并且不存在任何一个点同时在两个部分中,即\nexists x\in V-\{w\} ,x\in U_w\ \wedge\ x\in V_w
(可以\exists x\in V,x\notin U_w\ \wedge\ x\notin V_w,也就是这里的划分不是严格的。后面证明的时候不会再提及这一点)
-
在上述的划分中,\forall u\in U_w,d_{D}^-(u)=d_{D[U_w]}^-(u),也就是分出来的子图D[U_w]的点入度和D保持一样
-
DAG必然存在入度为0的结点
引理<1><2><3>是为了引理<4>的证明,但是引理<4>本身存在一个不需要前三个引理的证明
-
单向连通的DAG有且只有一个入度为0的点
-
对于单向连通的有向图D=<V,E>,去掉一个入度为零的点后,剩余点导出的子图一定也是单向连通的
符号语言表述:对于单向连通的有向图D_0=<V_0,E_0>,若有w\in V_0\ \wedge\ d_{D_0}^-(w)=0,设V_1=V_0-\{w\},则D_1=D_0[V_1]必然是单向连通的
-
对于一张一般的单向连通有向图D=<V,E>
设V'=V/\leftrightarrow(也就是V'是V关于“相互可达”关系的商集)
设E'=\{<V_u,V_v>\ |\ V_u\in V'\ \wedge\ V_v\in V'\ \wedge\ (\ \exists u,v(<u,v>\in E\ \wedge\ u\in V_u\ \wedge\ v\in V_v)\ )\}
则图D'=<V',E'>一定是单向连通的DAG
(实际上7就是算法竞赛中强连通分量缩点的过程)
引理<1>证明
引理<1>内容:DAG的子图一定是一个DAG
证明:
如果DAG的子图不是DAG,也就是有圈,那么其自身一定也有圈。所以DAG子图一定是DAG
引理<2>证明
引理<2>内容:对于有向图D=<V,E>,若其为DAG,那么对于\forall w\in V,必然可以将除了w剩下的点集V-\{w\}划分成两个部分:U_w和V_w,其中\forall u\in U_w,u\to w、\forall v\in V_w,w\to v,并且不存在任何一个点同时在两个部分中,即\nexists x\in V-\{w\} ,x\in U_w\ \wedge\ x\in V_w
证明:
因为如果存在这么一个x的话,必然有x\to w\ \wedge\ w\to x,即D有圈,产生矛盾
引理<3>证明
引理<3>内容:在引理<2>的划分中,\forall u\in U_w,d_{D}^-(u)=d_{D[U_w]}^-(u),也就是分出来的子图D[U_w]的点入度和D保持一样
证明:
这里复述一下引理<2>:对于有向图D=<V,E>,若其为DAG,那么对于\forall w\in V,必然可以将除了w剩下的点集V-\{w\}划分成两个部分:U_w和V_w,其中\forall u\in U_w,u\to w、\forall v\in V_w,w\to v,并且不存在任何一个点同时在两个部分中,即\nexists x\in V-\{w\} ,x\in U_w\ \wedge\ x\in V_w。
我们再定义V_r=V-U_w-V_w,也就是V_r中的点\forall v_r既不满足v_r\to w也不满足w\to v_r
假设u\in U_w的d_{D[U_w]}^{-}(u)\neq d_{D}^-(u)
首先显然不可能出现子图某个结点的入度大于母图的,也就是不可能d_{D[U_w]}^{-}(u)>d_{D}^-(u),所以我们的假设可以变成d_{D[U_w]}^{-}(u)<d_{D}^-(u)
如果发生了d_{D[U_w]}^{-}(u)<d_{D}^{-}(u),必然发生下面三种情况中的至少一种,但是这三种情况都会导致矛盾:
-
\exists v\in V_w,<v,u>\in E
这时必有u\to w,w\to v,v\to u,也就是产生了圈,与D是DAG矛盾
-
<w,u>\in E
同样,这时必有u\to w,w\to u,也就是产生了圈,与D是DAG矛盾
-
\exists v_r\in V_r,<v_r,u>\in E
因为u\to w,而v_r\to u,所以应该有v_r\to w,但是这与v_r\notin U_w矛盾
所以假设错误,因此引理<3>得证
引理<4>证明
引理<4>内容:DAG必然存在入度为0的结点
证明:
设D_0=<V,E>是一张DAG,我们一定可以逐次求D_k中某一点w的U_w,然后令D_{k+1}=D_{k}[U_w],由引理<1>可知D_{k+1}一定是DAG。很容易看出来|V(D_{k+1})|<|V(D_{k})|,也就是这个图是不断缩小的,所以一定存在某一次D_k导出的D_{k+1}=U_w=\varnothing,也就是没有任何一个点可达w,也就是d_{D_{k}}^{-}(w)=0
根据引理<3>,可以得到d_{D_{0}}^-(w)=d_{D_{1}}^-(w)=\cdots=d_{D_{k}}^-(w)=0,也就是D_0这个DAG存在入度为0的点
另一种证明,来自CSDN一个12年的帖子:
证明DAG必然存在入度为0的点等同于证明DAG必然存在出度为0的点
假如图中不存在出度为0的点,则所有点均有边指向另一点,设总点数为N,从任意一点沿任意一条边前往下一点N次,则总路径为N边N+1点,N+1点中必有两点为同一点,则这两点之间的N条边构成1环,则此图为有环图
使用的是鸽巢原理。。。妙啊
引理<5>证明
引理<5>内容:单向连通的DAG有且只有一个入度为0的点
证明:
首先由引理<4>知一定有入度为0的点
假设有两个入度为0的点u,v,由于D单向可达,故不妨让u\to v,那么存在通路\Gamma =uw_1\cdots w_kv,也就是有边<w_k,v>,这与v入度为0矛盾。所以只有一个入度为0的点
引理<6>证明
引理<6>内容:对于单向连通的有向图D=<V,E>,去掉一个入度为零的点后,剩余点导出的子图一定也是单向连通的
符号语言表述:对于单向连通的有向图D_0=<V_0,E_0>,若有w\in V_0\ \wedge\ d_{D_0}^-(w)=0,设V_1=V_0-\{w\},则D_1=D_0[V_1]必然是单向连通的
证明:
对\forall u,v\in V_1,有u,v\in V_0,并且由于D_0单向连通,所以一定存在从u到v的通路\Gamma(u,v),且通路中一定没有w。因为如果有的话就说明有边能到w,这与d_{D_0}^-(w)=0矛盾。正因为\Gamma(u,v)中没有w,所以\Gamma(u,v)在D_1中也一定是存在的
因此D_1是单向连通的
引理<7>证明
引理<7>描述:
对于一张一般的单向连通有向图D=<V,E>
设V'=V/\leftrightarrow(也就是V'是V关于“相互可达”关系的商集)
设E'=\{<V_u,V_v>\ |\ V_u\in V'\ \wedge\ V_v\in V'\ \wedge\ (\ \exists u,v(<u,v>\in E\ \wedge\ u\in V_u\ \wedge\ v\in V_v)\ )\}
则图D'=<V',E'>一定是单向连通的DAG
证明:
首先证明D'是无环的,也就是是一张DAG
假设D'有环,也就是\exists V_u,V_v\in V',V_u\leftrightarrow V_v,那么在D中必然存在u\in V_u,v\in V_v,使u\leftrightarrow v,也就是在D中V_u和V_v中有点可以互相到达,这必然导致V_u与V_v中任何一对点都是互相可达的,这与V_u,V_v\in V/\leftrightarrow矛盾。所以D'一定是有环的
再证明D'是单向连通的
## 对于DAG情况的构造
我们会先构造DAG上的通路,也就是证明:对于DAG $ D=<V,E>$,$D$是单向连通图 可以推得 $D$中存在经过每个顶点至少一次的通路
(复述下,在最开始就说了,不考虑$D$中的自环和平行边)
之后再考虑一般有向图上的构造
为了方便查看引理,我们把需要用到的引理搬过来:
引理<5>:单向连通的DAG有且只有一个入度为0的点
引理<6>:对于单向连通的有向图$D=<V,E>$,去掉一个入度为零的点后,剩余点导出的子图一定也是单向连通的
符号语言表述:对于单向连通的有向图$D_0=<V_0,E_0>$,若有$w\in V_0\ \wedge\ d_{D_0}^-(w)=0$,设$V_1=V_0-\{w\}$,则$D_1=D_0[V_1]$必然是单向连通的
对于单向连通DAG:$D_0=<V_0,E_0>$,我们有如下过程:
1. 从$D_k$中找到(唯一的)入度为0的点$w_k$,根据引理<5>,这个点一定存在且只有一个
2. 令$V_{k+1}=V_k-{w_k}$,$D_{k+1}=D[V_{k+1}]$,根据引理<6>,$D_{k+1}$也是单向连通的DAG。之后执行过程 1.,直到$V_{k+1}=\varnothing
在D_0中一定有边<w_k,w_{k+1}>,因为w_{k+1}是D_{k+1}中入度为0的点,而在D_{k}中这个点入度并不为0,也就是删去w_k导致了w_{k+1}的入度变成0,也就是在D_{k}中有边<w_k,w_{k+1}>,因此在D_0中有边<w_k,w_{k+1}>
这实际上就是拓扑排序的过程,只不过由于单向连通DAG只有一个入度为0的点,所以每一次都只会排出一个点
排出的点按顺序构成的\Gamma=w_0w_1\cdots w_{|V_{0}|-1}就是要求的通路
对于一般图情况的构造
也就是证明:对于 D=<V,E>,D是单向连通图 可以推得 D中存在经过每个顶点至少一次的通路
(复述下,在最开始就说了,不考虑D中的自环和平行边)
搬一下引理<7>:
对于一张一般的单向连通有向图D=<V,E>
设V'=V/\leftrightarrow(也就是V'是V关于“相互可达”关系的商集)
设E'=\{<V_u,V_v>\ |\ V_u\in V'\ \wedge\ V_v\in V'\ \wedge\ (\ \exists u,v(<u,v>\in E\ \wedge\ u\in V_u\ \wedge\ v\in V_v)\ )\}
则图D'=<V',E'>一定是单向连通的DAG
还需要补充很重要的一点:
补充:对于\forall V_u\in V',由定义其内部的点在D中必然是相互可达的,并且存在一个回路,其起点和终点均为\forall u\in V_{u},并且经过V_u中所有点(即强连通图的判定定理“对于有向图D=<V,E>,D是强连通图 当且仅当 D中存在经过每个顶点至少一次的回路”),我们将这个回路写成\Gamma'_{V_u}(u)
对于任何一张有向图D=<V,E>:
-
通过引理<7>的方法求出D'=<V',E'>,然后根据DAG情况的构造得到\Gamma_W=W_0W_1\cdots W_{|V'|-1}
-
我们从W_k中取两点x_k,y_k(允许x_k=y_k),由定义,无论怎么取,x_k\leftrightarrow y_k,我们记x_k到y_k的通路为\Gamma (x_k,y_k)
-
因为<W_k,W_{k+1}>\in E'\ \Leftrightarrow\ \exists u\in W_k,v\in W_{k+1},u\to v(根据引理<7>里面的定义可知),我们记u\to v的通路为\Gamma_D(u,v)
于是就可以构造出通路了\Gamma =\Gamma'_{W_0}(x_0)\Gamma(x_0,y_0)\Gamma_D (y_0,x_1)\ \Gamma'_{W_1}(x_1)\Gamma(x_1,y_1)\Gamma_D (y_1,x_2)\ \cdots
其中\Gamma'_{W_k}(x_k)的存在性由前面的“补充”得到,\Gamma(x_{k},y_{k})由"2."得到,\Gamma_D(y_k,x_{k+1})的存在性由“3.”得到
这个通路可以看作是:“遍历强连通分量内点,在强连通分量内找到前往下一个强连通分量的出口,从出口到下一个强连通分量”的过程
构造完毕
# 后记
## 概述
整个证明的流程就是如图了
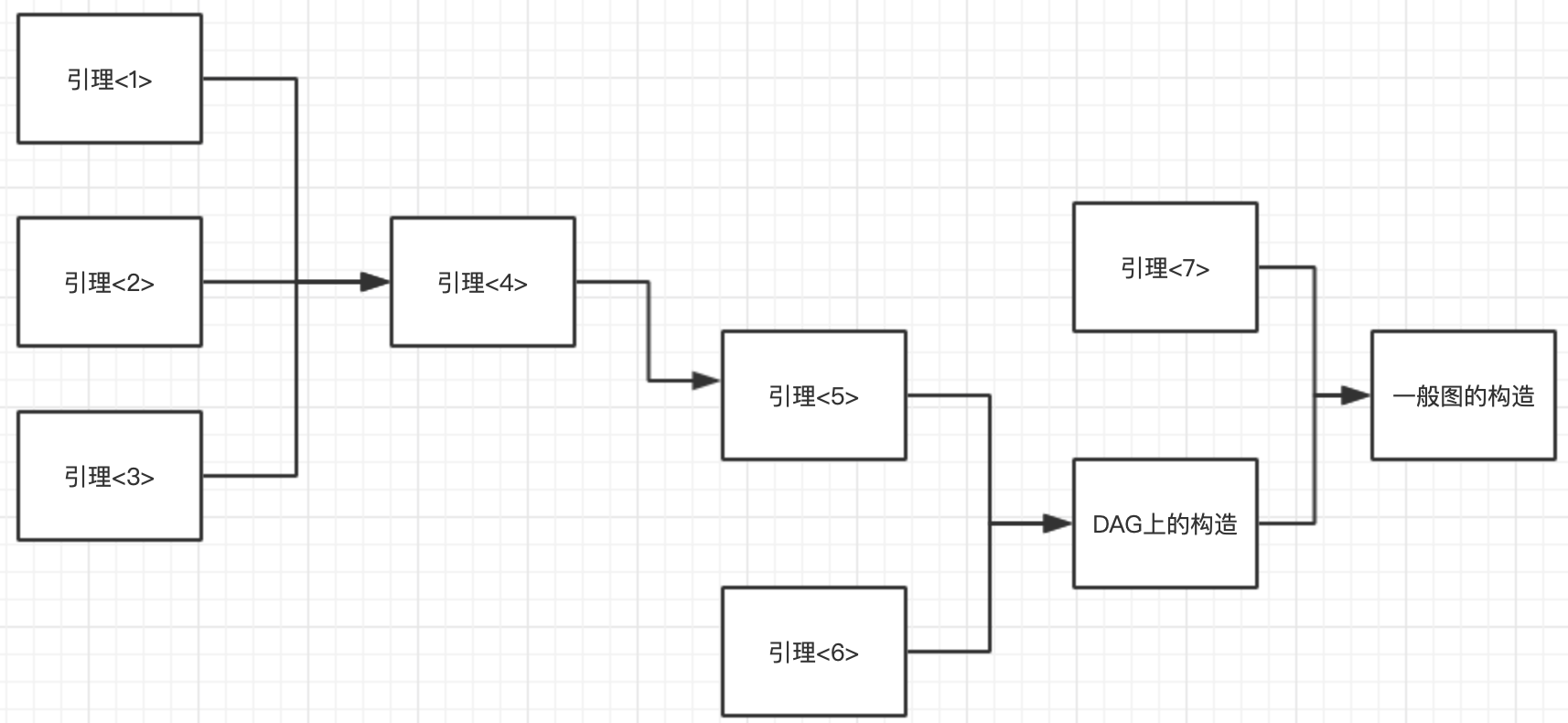
证明的关键是引理<5>,构造是建立在引理<5>的基础上的
引理<4>也可以直接证明
## 感受
实际上想到“遍历强连通分量内点,在强连通分量内找到前往下一个强连通分量的出口,从出口到下一个强连通分量”并没有花费太长时间,整个证明过程中最花时间的有两个部分:
1. 证明“DAG必然存在入度为0的结点”,也就是引理<4>
这个结论非常显然,显然到对它的证明需要3个引理支撑
(引理<4>的证明一种方法是使用引理<1><2><3>证,但是也有另一种方法证,是来自互联网的,更简单,上面都写了。。。看来还是菜了啊)
2. 将想法写成相对严谨的语言
就像前面说的,想到“遍历强连通分量内点,在强连通分量内找到前往下一个强连通分量的出口,从出口到下一个强连通分量”并没有花费我太多时间,我也相信大多数ACMer能很快地想到这个做法。但是怎么使用足够严谨地描述这个过程就很头疼了。最后这个文章的效果可能也有些“不说人话”了233
## 被秒杀了
犯了研究的一个大忌:在研究前不充分调研是不是有人做过同样的事情了
在百度知道的[这个回答](https://zhidao.baidu.com/question/2080282964970140228.html),答主提出了更短而精巧的方法证明,先假设了“经历的不同顶点的个数最多的通路”的存在,然后通过反证证明了这个通路经过了所有的结点。。。这么看我的方法简直就是极端暴力、一点都不优雅,唯一可取的(自我安慰的)就是提出了这条通路应该怎么走吧
反思过来,引理<4>当时想到可能可以用容斥原理了,但是并没有想到到底应该怎么容斥,再加上思考过程中想到了现在的解法,就没有深究了
而整个证明过程都受到了书上定理14.8的构造证明的影响,导致一直在想的是怎么构造,也失去了考虑更好的方法的契机。。