思维链
Tom17
·
·
个人记录
1. 如何将子集 DP 的 O(3^n) 优化到 O(2^n \textrm{poly}(n))?
考虑每次不枚举子集,而是枚举关键元转移:具体地,枚举一个元素,然后从除去这个元素即补集转移过来。
这两题需要分组,使得最大化 sum=0 的集合数量。发现 O(3^n) 是简单的。考虑枚举关键元,发现我们似乎还要记录一维表示最后一个集合的 sum。这样变为 O(2^nnV),比朴素还要劣。
我们把分组看作用一些隔板间隔开集合(把集合拍在序列上),我们既可以最大化集合的数量,也可以最大化隔板的数量。我们只考虑 sum=0 的集合。发现我们可以放一个隔板当且仅当前缀 sum=0。直接 DP 即可。
这启发我们能否将子集转换为关键元,并在本身状态(或者只加 \textrm{poly}(n))的状态本身的性质去转移。
- AT_abc432_f
- P7718 「EZEC-10」Equalization
2. 贡献尽量在小(简短)的地方转移,即尽量将贡献记在一个集中的地方,而非记在连续或散列的地方
可能有些抽象。就是说:如果一个状态可以以一个点出现的形式被记录,那就不要将其放在一段连续的或者散列的状态中记录。
1. B3609. 【NOI2025模拟】计树
考场上记录的状态为:从后向前考虑,至到当前点时:后方缺儿子的点数量:分为能加儿子的点,和强制加儿子的点,后方恰好没有父亲的点的数量。这样就变为了 O(n^4) 的。另一个问题 A 也有存在,但是这里不论,放于注释。但是为什么要分两个状态来考虑呢?
可以这样:我们把当前点是否要加两个儿子放在了添加第二个儿子的时候决策。 但是你发现说:添加第二个儿子时,第二个儿子没有提供任何有效的信息来辅助这个决策,即发现这个第二个儿子是谁无关当前点是否选择第二个儿子。
至于为什么无关,因为你排序后(按序考虑)已经为转移提供了一个完序关系,你不再需要考虑前后的偏序了,所以对于这种只关心偏序的,就不应该把其记录在状态里面,而是应该当前就决策好(钦定好),不要把后效性带到后面去。
也即是说:如果一个状态可以以一个点出现的形式被决策,那就不要将其放在一段连续的状态带着一起转移。
2. B3604. 【NOIP2025模拟】账本
考场上差点没想出来。
贪心时简单的,从前往后如果某个位置小于 0 则翻转,使得一个后缀加。
发现我们的决策点是在每个 <0 的位置。这显然是 O(n) 的。 如果决策点互不影响时,可以拿数据结构维护。但是现在前面的决策点修改后,会使得将后面的决策点也发生改变。
考虑我们是否可以将每次的决策的贡献缩在一个点上面?
我们发现:首先每次决策具有偏序性,即后面一个点的决策值一定比前面要小。想到偏序性就要想到极值元,即最大元/最小元。 我们注意到最小元抬升完毕后,后面就不可能有元素继续抬升,否则当前就不是最小元。
我们注意到贡献只与前缀值最小元有关。这个题就做完了。
但是如何归纳这个问题?就是如果一串点的贡献是将后缀影响的时候,我们需要观察能否将贡献挂在(转移到,写作成)最后一个点/极值元的贡献。即把一串点的贡献归到一个点的贡献。
3. 树上维护一级邻域信息,考虑把贡献分为儿子和父亲,修改时把父亲一起修改,查询时,只查询儿子的贡献和,和父亲的贡献
- P9194 [USACO23OPEN] Triples of Cows P
未删除为黑点,否则为白点。
黑点有贡献,设其可以不跨过另一个黑点所能到达的黑点数量为 k,则其贡献为 k^2-k。
考虑从全部黑点开始,不断删除黑点。(这里用到了正难则反(双边考虑)的思想,因为要用到的并查集只支持合并,不支持删除。)
把一个极大的白色连通块及其挂着的黑色点合并在一起考虑。
4. 类 ARC 的序列题 1:元素删除,考虑终态,并找一些必要性把终态不对的排除掉
A5605【NOIP2025模拟】区间操作
考虑 **终态**,有终态为这些序列及其前缀:
$$
1,1,1\\
1,2,3\\
2,1,2\\
2,3,2\\
3,2,1\\
3,3,3,\cdots
$$
终态可以考虑能否将一段区间完全删除掉。
考虑枚举一些必要性。一段区间删除的必要性第一是区间和对 $4$ 取模为 $0$。**你发现说前 $5$ 种情况已经可以被排除掉了。**
当推出一个必要性时,要分析什么情况下有情况满足这个必要性之后还不合法。然后我们将终态 **分为** 这些情况,并讨论出来只有最后这种全是 $3$ 的情况没有被判掉。
然后就对最后这种情况进行必要性分析。发现其不删掉当且仅当周围不够 $1$ 和 $2$ 来删掉。
每个 $1$ 可以删掉一个 $3$。每个 $2$ 可以删掉两个 $3$。证明其是必要的。可以用构造证明。考虑归纳。注意归纳之后就可以变为**贪心删除**。最后证明一下即可。
**注意讨论这里的时候要把区间和对 $4$ 取模为 $0$ 这个先验必要性考虑到。**
#### 5. (指数)根号分治应当如何去做
[QOJ 3086. Edge Subsets](https://qoj.ac/problem/3086) / [B5522. 【1.14省选模拟】卡了就卡过](http://oi.bashu.cn/p/B5522)
对于这种一看 $n\le 200$ 左右的图论问题,一眼就是指数分治的模型的时候,我们要做的,就是去**充分讨论**当某个值大的时候怎么办,某个值小的时候怎么办?
本质上就是找到一个合适的偏序使得树宽尽可能小。
四个问题:
1. BFS 如果不连续,怎么写代码
2. 观察的双面性
3. 分治 15 20 和 2*n/c2 的直觉
4. 大于小于,最大值/最小值
我们思考一下部分分,发现 A 性质可能有提示作用。$c_1,c_2\le 15$,就是说 $c_1,c_2$ **均**小于 $15$,反面就是存在一个大于 $15$ 的。
不要一开始就把问题摊到平面图上考虑。因为它是两个不同的问题,我们需要思考两遍。并且一般我们如果在原来的思维路径上思考时,我们会将其摊到序列上考虑。
我们画出来在序列上的样子,直接可以发现,后效性只和后 $15$ 个点有关系。所以复杂度是 $O(2^{15}\textrm{poly}(15))$ 的。
我们设 $B=15$ 当存在一个大于 $15$ 的,说明在那一边,宽度只有 $\frac n B$。然后我们需要记录上面和下面的状态,使得总状态数为 $2^{\frac {2n} B}$。
先不要代值进去,先列出来:$2^B$ 和 $2^{\frac {2n} B}$ **发现平衡时 $B$ 取到 $20$ 而不是 $15$**。
所以为什么当时带入 $2^{\frac {2n} B}$ 为 $15$ 是就会发现很不对劲,这个复杂度严重超标了。因为题目给到的分治可能不一定是最优分治。
所以我们要注意两个问题:
1. **根号分治的思考,注意每种思考思考不出来都要重新从头开始思考,并且要注意是否要进行所谓的第一步转换。**
2. **根号分治不要先入为主的代数字进去,而是要写作 $B$ 只有列到最后,用 $B$ 表示出来时才有最优复杂度。**
还有,怎么判断是用 $\max(c_1,c_2)$ 还是 $\min(c_1,c_2)$ 分治呢?一个方法是看“跨度”,如果两个都小,那么总体在数轴上的跨度就小,我们用数轴分析;如果存在一个跨度比较大,那么每个同余类的大小就不会太大,且注意到,$\bmod c_1$ 的某个同余类,不论哪一个数加上 $c_2$ 都会变到 **相同的** 另一个 $\bmod c_1$ 的同余类。
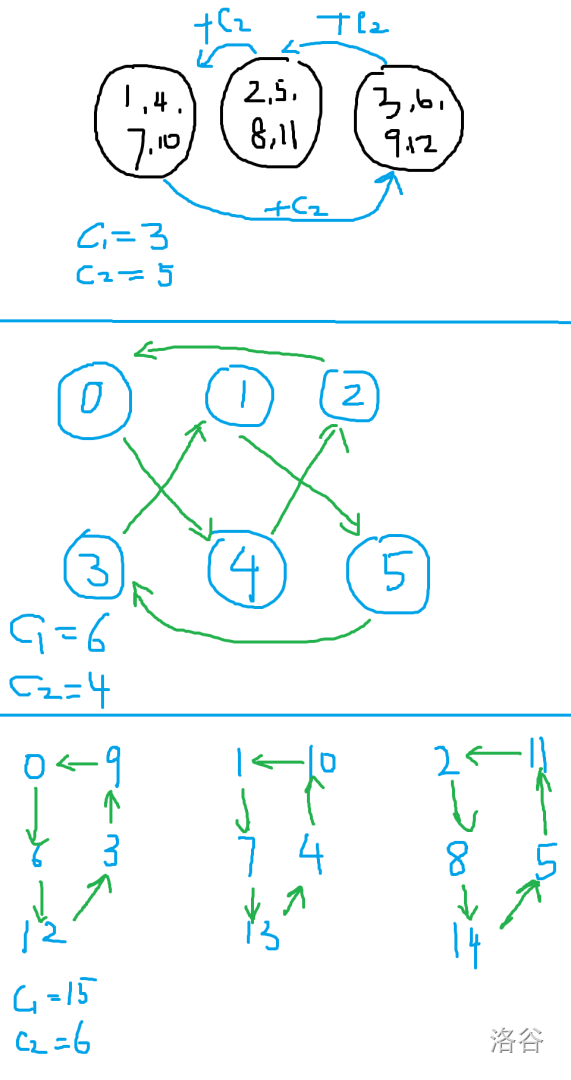
(上述每个点均表示一个同余类。)
可以看到,其形成了 $g=\gcd(a,b)$ 个相同的结构,每个结构形成了一个跨边长度为 $c_2$,大小为 $\frac {c_1}{g}$ 的环。
所有我们可以断环为链,然后就将断边记录下来,即为 $2$ 倍同余类大小的状态数。
代码直接写就可以了。
#### 6.
如何从多项式较高复杂度优化到较低复杂度?
**[P8290 [省选联考 2022] 填树](https://www.luogu.com.cn/problem/P8290)**
原思考路径:
> 1. 首先枚举树链,这里是 $O(n^2)$ 的。
> 2. 然后枚举最大值 $M$ 那么权值区间在 $[M-K,M]$ 之间。发现每个点的方案数关于 $M$ 是一个分段一次函数。把其分成 $O(n)$ 段。
> 3. 然后每一段变为若干个一次函数的乘积在一段上的前缀和,使用拉插算出系数后转前缀和,这里是 $O(n^2)$ 的。
> 4. 发现会算重,也就是说我们要钦定最大值必须取到,所以要对于点来说,我们定一个序,然后枚举某个点,并钦定其为最后一个取到最大值的点,然后再算一遍。这里是 $O(n)$ 的。
>
> 总共是 $O(n^2)\times O(n) \times O(n^2) \times O(n)=O(n^6)$。只能勉强过 $n=30$ 的点。
首先就可以把最后一个 $O(n)$ 给优化掉。发现 能取到最大值的 等于 全部 减去 不能取到最大值的。对于每个 $M$,直接减去 $[M-K,M-1]$ 的方案。
*当时也想到,但是觉得这样做,在做 $[M-K,M-1]$ 的方案时,就要把这个也如之前那样要钦定要选到最大值。最后就会不断规约,变为 $\le K$ 大小的区间都要取到。*
但这样想是错误的,因为你是容斥掉不能选到最大值的方案,对内部选不选 $M-1$ 没有要求。
并且我们也想到另一个刻画这种东西的思路,对于某一个长度为 $P$ 的区间,它恰好在 $K-P+1$ 个长度为 $K$ 的区间中被计数,而容斥的时候,恰好在 $K-P$ 个长度为 $K-1$ 的区间被容斥掉,所以最后的总系数为 $1$。
也就是说,我们想要计数所有长度 $\le M$ 的区间,等于所有长度等于 $M$ 的区间的内部区间的和,减去所有长度等于 $M-1$ 的区间的内部区间的和。
然后就是另一个比较重要的优化。
发现说:一个多项式算前缀和是非常耗时间的,但是因为如果我们把区间剖出来之后,每一段的左右端点的固定了的。也就是说,对于每一条树链,其在这里所要算的前缀和区间是固定的。
又因为转前缀和具有线性性(参考 FWT 点值相加),所有我们可以把所有多项式加起来再做前缀和。
在没做换根优化前,我们有 $O(n^3)$ 个多项式,我们加起来再做已经可以做到 $O(n^4)$ 了(与多项式总长度同阶)。卡卡可能可以通过。
我们考虑优化多项式数量。
我们可以把外层为枚举每个段,然后每个点就变为一个一次多项式。需要求每一条链多项式乘积的和。
直接树形 DP 发现每个点存的多项式总长度是 $O(n^2)$ 的,加上一些转移就可以单段 $O(n^3)$。合并就是 $O(n^4)$ 的。
使用用值表示多项式的方法,先代入若干个值,算出来再转为前缀和。
你发现说,我们既然要算前缀和,那么我们将这个 $i=1,2,3,\cdots$ 代入,然后算前缀和再插值即为答案。
也就是说,算一个 $k$ 次函数 $F$ 的前缀和函数,算出来 $i=1,2,\cdots,k+2$ 的 $F(i)$ 值,求前缀和 得 $SF(i)$,把 $(i,SF(i))$ 插值算出来的多项式即为答案。
这就不用转系数这么麻烦了。
*呀呀呀,漏看了还要算权值和。*
还是这样,先切开若干段,然后每个点的权值就变为了一个关于最大值的二次多项式,然后像上面那样代入即可。