紫题算法学习实况
quest_2
·
2020-10-19 20:07:42
·
个人记录
因为进不去复赛就只能休养休养生息,整点算法学学。和同机房的神仙相比,窝挖的坑实在是太多了 OvO 。
2020-10-21:竟然与he老爷讲课撞车了,两相对比显然突出窝的菜
2020-11-16:CSP-S又垫底了,可以安心写博客力
2020-12-26:该文章已停更,光标几乎卡的动不了了
《实况一》(本文)中包含的内容:
点分治
“每天就是切一些 N 倍经验题,维持维持生活这样子。”
处理什么问题:
大部分是树上点对距离问题,当然还有一些变形。(树论毒瘤爪巴)
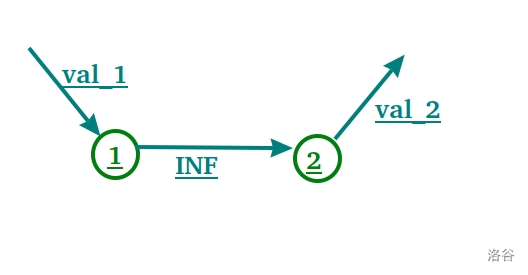
如果给您一棵树,让您查询树上是否存在两点距离为 K 。您没学过点分治,您怎么做?
您说,您会暴力 O(n^2) 枚举点对查询其距离!
抱歉,点分治是可以 O(n\log n) 的。
思想是什么:
现在讲一下思想。
树上两点之间,路径唯一 ,两点通向LCA的路径的并 ,即为两点之间的路径。
这种路径要分类无非两种:过 全树的根 结点的,和 不过根 结点的。
或者换种说法,LCA是全树的根结点的,或者不是根结点的。
(超喜欢这个字体 AwA )
分类讨论绝对是树学界存在的最恶心的玩意。不会真的有人在代码里分类讨论吧,不会吧不会吧。
我想把这两种情况 归为一类 。
大眼观察法看出 Type\ 2 在以粉色点为根的时候就可以归纳为一种 Type\ 1 。
显然,我们要从根结点一层一层地递归下去求解。
获得了 $O(level\cdot n)$ ( $level$ 是树的深度)的优秀复杂度!
然后当场就被链卡回了 $O(n^2)$ 。
我们发现,它被卡了,究其原因就是因为树的形态太 $hentai$ 。
一棵树,存不存在距离为 $K$ 的点对,和让谁来当根有关系吗?
没有关系。
那我们就该选一个好亿点的点来当根哇。
这个“好亿点”,具体指的就是,以它来当根,能使 **树的深度最小** 。
##### 这里有一个概念叫树的重心:
我们知道在一棵树上,删去一个点后,剩下的部分必然不联通。
如果一个点删去它后,剩余的几部分中 **大的那一块最小** ,则我们说这个点是这个树的重心。
不难感觉到,如果以一棵树的重心为根,它的佐佑两边会最为“平衡”。
在最美好的愿景下,每层以重心作根可以做到把树二等分。
那二等分又二等分,最终能控制在 $\log n$ 的递归层数。
获得了 $O(n \log n)$ 的优秀复杂度!(大喜)
撒花撒花~
#### 劲爆习题:
**模板题:**[P3806 【模板】点分治1 ](https://www.luogu.com.cn/problem/P3806) :(想不到叭,模板就是紫的 $QwQ$ )
给定一棵有 $n$ 个点的树,询问树上距离为 $k$ 的点对是否存在。
裸题,8说了,该说的都在注释里。
```cpp
#include <bits/stdc++.h>
using namespace std;
const int MAX = 1e5 + 7;
const int INF = 1e9 + 7;
/*前向星存图组件*/
struct edge
{
int to, next;
int val;
} e[MAX << 1];
int N, M, SUM;
int head[MAX], eid = 0;
void adde(int x, int y, int w)
{
e[++eid].to = y;
e[eid].next = head[x];
e[eid].val = w;
head[x] = eid;
}
/*求重心组件*/
int cent;//指重心的编号
int size[MAX], son[MAX];//size:其子树(包括自己)的大小 son:最大儿子的大小
int vis[MAX];
void getroot(int u, int lst)
{
size[u] = 1;
son[u] = 0;//初始化
for (int i = head[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == lst || vis[v])
{
continue;
}
getroot(v, u);
size[u] += size[v];
son[u] = max(son[u], size[v]);//更新最终儿子
}
son[u] = max(son[u], SUM - son[u]);//可能子树外的部分更大
//SUM实时更新成当前要求重心的树的大小
if (son[u] < son[cent])
{
cent = u;//更新
}
}
/*点分治组件*/
int dis[MAX], apr[MAX], cntapr;
//dis:到“当前处理到的子树”的根结点的距离
//apr:一个子树级别的桶,存所有出现过的距离
//cntapr:桶大小
void getdis(int u, int lst)
{
apr[++cntapr] = dis[u];//装桶
for (int i = head[u]; i; i = e[i].next)
{
int v = e[i].to, w = e[i].val;
if (v == lst || vis[v])
{
continue;
}
dis[v] = dis[u] + w;//更新距离
getdis(v, u);
}
}
int query[MAX], ans[10000007], judge[10000007];
//query:询问,这里采用离线回答做法
//ans:对于每一个询问的答案(0/1 表示有或没有)
//judge:一个整树级别的大桶
queue<int> clear;
void calc(int u)
{
for (int i = head[u]; i; i = e[i].next)//这里是遍历每一棵子树
{
int v = e[i].to;
if (vis[v])
{
continue;
}
int w = e[i].val;
dis[v] = w;
cntapr = 0;//清桶
getdis(v, u);//这里是往下搜(遍历到的这棵子树)
for (int j = 1; j <= cntapr; j++)
{
for (int k = 1; k <= M; k++)
{
if (query[k] - apr[j] >= 0 && judge[query[k] - apr[j]])//若和他拼起来能达到K的距离出现过
{
ans[k] = 1;//则这是可拼出K的答案
}
}
}
for (int i = 1; i <= cntapr; i++)
{
clear.push(apr[i]);
judge[apr[i]] = 1;//装大桶
}
}
while (!clear.empty())
{
judge[clear.front()] = 0;
clear.pop();
}
}
void solve(int u)
{
judge[0] = 1;
vis[u] = 1;
calc(u);
for (int i = head[u]; i; i = e[i].next)
{
int v = e[i].to;
if (vis[v])
{
continue;
}
SUM = size[v];
son[0] = INF;
cent = 0;
getroot(v, 0);//获取新重心
solve(cent);//以重心为根递归
}
}
int main()
{
cin >> N >> M;
for (int i = 1.; i < N; i++)
{
int fr, to, val;
cin >> fr >> to >> val;
adde(fr, to, val);
adde(to, fr, val);
}
for (int i = 1; i <= M; i++)
{
cin >> query[i];
}
son[0] = SUM = N;
getroot(1, 0);
solve(cent);
for (int i = 1; i <= M; i++)
{
if (ans[i])
{
cout << "AYE\n";
}
else
{
cout << "NAY\n";
}
}
}
```
**次模板题:**[P4178 Tree](https://www.luogu.com.cn/problem/P4178)
由上题的询问存在与否变成了询问 **点对数** ,要求变成了 **小于等于** 。
点分治的板子该打还是打,但要改一下 $\operatorname{calc}$ 函数。
**上一题的策略是**:存桶,查能和它拼成 $K$ 的距离是否存在。
但我们这么整是因为题目要求的是等于 $K$ ,所以能拼的距离是唯一确定哒。
可这题是不确定的,所以得换一种思路。
我们尝试把所有出现过的距离排个序,有两个指针 $L$ 和 $R$ 从数组两边往中间逐步压缩。
$L$ 指向的距离和 $R$ 指向的距离,会拼出一种可能的距离。
可以证明这样能不重不漏地拼出树上存在的每一种 **两点距离** 。
甚至可以在线/fad/fad 。
```cpp
#include <bits/stdc++.h>
using namespace std;
#define debug cout
const int MAX = 1e5 + 7;
struct edge
{
int to, next;
int val;
} e[MAX];
int head[MAX], eid = 0;
void adde(int x, int y, int w)
{
e[++eid].to = y;
e[eid].next = head[x];
e[eid].val = w;
head[x] = eid;
}
int size[MAX], son[MAX], cent, vis[MAX];
int N, M, SUM, K;
void getroot(int u, int lst)
{
size[u] = 1;
son[u] = 0;
for (int i = head[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == lst || vis[v])
{
continue;
}
getroot(v, u);
size[u] += size[v];
son[u] = max(son[u], size[v]);
}
son[u] = max(son[u], SUM - son[u]);
if (son[u] < son[cent])
{
cent = u;
}
}
int dis[MAX], apr[MAX], cntapr = 0;
void getdis(int u, int lst)
{
apr[++cntapr] = dis[u];
for (int i = head[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == lst || vis[v])
{
continue;
}
dis[v] = dis[u] + e[i].val;
getdis(v, u);
}
}
int ans, query[MAX];
int calc(int u, int w)
{
dis[u] = w;
cntapr = 0;
getdis(u, 0);
sort(apr + 1, apr + 1 + cntapr);
int answer = 0;
for (int l = 1, r = cntapr; l < r;)
{
if (apr[l] + apr[r] <= K)
//若这两种距离拼出的长度小于等于K
{
answer += r - l;
//那么r取他们之间的其他数也会小于等于K
//因为排过序了,r往左移只会更小
l++;
}
else
r--;//否则就取更小的r
}
return answer;
}
void solve(int u)
{
ans += calc(u, 0);
vis[u] = 1;
for (int i = head[u]; i; i = e[i].next)
{
int v = e[i].to, w = e[i].val;
if (vis[v])
{
continue;
}
ans -= calc(v, w);
SUM = size[v];
cent = 0;
getroot(v, u);
solve(cent);
}
}
int main()
{
cin >> N;
for (int i = 1; i <= N - 1; i++)
{
int fr, to, val;
cin >> fr >> to >> val;
adde(fr, to, val);
adde(to, fr, val);
}
cin >> K;
cent = 0;
SUM = son[0] = N;
getroot(1, 0);
solve(cent);
cout << ans << endl;
}
```
**次次模板题:**[[国家集训队]聪聪可可](https://www.luogu.com.cn/problem/P2634)
这回求的是距离是 $3$ 的倍数的点对数。照样改 $\operatorname{calc}$ 。
带了亿亿亿亿亿点思维,但是易见平凡(雾。
装桶的思路还是不变,但是开这么多桶贞德合理吗?
两个数 $A,B$ 的 **和** $\bmod 3$ 余 $0$ 。则跑不出三种情况:
- $A \bmod 3=0 , B \bmod 3=0
A \bmod 3=1 , B \bmod 3=2
A \bmod 3=2 , B \bmod 3=1
开三个桶来计数,tong_0,tong_1,tong_2 分别存 \pmod 3=0,\pmod 3=1,\pmod 3=2 。
那么来个小加法原理就有了:
ans=tong_1\cdot tong_2\ +\ tong_2\cdot tong_1\ +\ tong_0\cdot tong_0
小心输出格式,甚至要约分。(淦
您吊打国集
#include <bits/stdc++.h>
using namespace std;
const int MAX = 2e4 + 7;
struct edge
{
int to, next;
int val;
} e[MAX << 1];
int head[MAX], eid = 0;
void adde(int x, int y, int w)
{
e[++eid].to = y;
e[eid].next = head[x];
e[eid].val = w;
head[x] = eid;
}
int N;
int size[MAX], son[MAX], SUM;
int vis[MAX];
int cent;
void getroot(int u, int lst)
{
size[u] = 1;
son[u] = 0;
for (int i = head[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == lst || vis[v])
{
continue;
}
getroot(v, u);
size[u] += size[v];
son[u] = max(son[u], size[v]);
}
son[u] = max(son[u], SUM - son[u]);
if (son[u] < son[cent])
{
cent = u;
}
}
int ans;
int tong[3], dis[MAX];
void getdis(int u, int lst)
{
tong[dis[u] % 3]++;//相应的桶++
for (int i = head[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == lst || vis[v])
{
continue;
}
dis[v] = dis[u] + e[i].val;
getdis(v, u);
}
}
int calc(int u, int w)
{
dis[u] = w;
tong[0] = tong[1] = tong[2] = 0;//先清空
getdis(u, 0);
return tong[1] * tong[2] * 2 + tong[0] * tong[0];
//如上公式算得答案
}
void solve(int u)
{
ans += calc(u, 0);
vis[u] = 1;
for (int i = head[u]; i; i = e[i].next)
{
int v = e[i].to, w = e[i].val;
if (vis[v])
{
continue;
}
ans -= calc(v, w);
SUM = size[v];
cent = 0;
getroot(v, u);
solve(cent);
}
}
void output()
{
int G = __gcd(ans, N * N);
cout << ans / G << "/" << N * N / G << endl;
}
int main()
{
cin >> N;
for (int i = 1; i <= N - 1; i++)
{
int fr, to, val;
cin >> fr >> to >> val;
adde(fr, to, val);
adde(to, fr, val);
}
SUM = N;
son[0] = SUM;
getroot(1, 0);
solve(cent);
output();
}次次次模板题 :[IOI2011]Race
刚爆踩完集训队,马上就IOI了(笑)
这题和纯模板题又有差别,在距离符合的情况下要求路径上边数最少。还是改 \operatorname{calc} 。
像这种多条件下求人上人的题目,多半是平衡树或堆。
因为要求的并非 全部路径 最优的一个,而是有条件限制(距离定为 K )。
所以只能打平衡树了……
吗?
人生苦短,我用 set+lower\_bound 。遍历所有出现过的距离,查找的是能和它拼成 K 的长度中边数最少的。
因为题目大毒瘤,所以加了亿点卡常。
#include <bits/stdc++.h>
using namespace std;
#define PII pair<int, int>
#define MP make_pair
#define SIT set<PII>::iterator
const int MAX = 2e5 + 7;
inline int Min(int x, int y)
{
return x < y ? x : y;
}
inline int Max(int x, int y)
{
return x > y ? x : y;
}
int read()
{
int num = 0, bj = 0;
char ch = getchar();
while (!isdigit(ch))
{
if (ch == '-')
{
bj = 1;
}
ch = getchar();
}
while (isdigit(ch))
{
num = num * 10 + ch - '0';
ch = getchar();
}
return bj ? -num : num;
}
struct edge
{
int to, next;
int val;
} e[MAX << 1];
int head[MAX], eid = 0;
inline void adde(int x, int y, int w)
{
e[++eid].to = y;
e[eid].next = head[x];
e[eid].val = w;
head[x] = eid;
}
int N, K, SUM;
int size[MAX], son[MAX];
int vis[MAX];
int cent;
inline void getroot(int u, int lst)
{
size[u] = 1;
son[u] = 0;
for (register int i = head[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == lst || vis[v])
{
continue;
}
getroot(v, u);
size[u] += size[v];
son[u] = Max(son[u], size[v]);
}
son[u] = Max(son[u], SUM - son[u]);
if (son[u] < son[cent])
{
cent = u;
}
}
set<PII> s;
int ans = 1e9 + 7;
PII apr[MAX];
int cntapr = 0;
int dis[MAX];
inline void getdis(int u, int lst, int path)
{
if (path > ans || dis[u] > K)
//到题解区学的剪枝,其实不难理解
{
return;
}
apr[++cntapr] = MP(dis[u], path);
//装桶,第一维是长度,第二维是路径上的边数。
for (register int i = head[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == lst || vis[v])
{
continue;
}
dis[v] = dis[u] + e[i].val;
getdis(v, u, path + 1);
}
}
inline void calc(int u)
{
s.clear();
s.insert(MP(0, 0));
for (register int i = head[u]; i; i = e[i].next)
{
int v = e[i].to, w = e[i].val;
if (vis[v])
{
continue;
}
cntapr = 0;//清空
dis[v] = w;
getdis(v, u, 1);
//现在 apr 数组里装得是v这棵子树上,各种新产生的路径
for (int j = 1; j <= cntapr; j++)
{
int d = apr[j].first, p = apr[j].second;
//取出距离和边数
SIT pos = s.lower_bound(MP(K - d, 0));
//查能拼的长度
if (pos != s.end() && pos->first + d == K)
{
ans = Min(ans, pos->second + p);//反复取min
}
}
//装进set
for (int j = 1; j <= cntapr; j++)
{
s.insert(apr[j]);
}
}
}
inline void solve(int u)
{
cent = 0;
getroot(u, u);
vis[cent] = 1;
calc(cent);
for (register int i = head[cent]; i; i = e[i].next)
{
int v = e[i].to;
if (vis[v])
{
continue;
}
SUM = size[v];
solve(v);
}
}
int main()
{
cin >> N >> K;
for (register int i = 1; i <= N - 1; i++)
{
int fr, to, val;
fr = read(), to = read(), val = read();
fr++;
to++;//因为这题的申必编号从0开始,所以全体编号加1处理
adde(fr, to, val);
adde(to, fr, val);
}
cent = 0;
SUM = son[0] = N;
solve(1);
if (ans == 1e9 + 7)
{
cout << -1 << "\n";
}
else
{
cout << ans << "\n";
}
}点分树(动态点分治)
“我真傻,真的,我以为三倍经验黑题躺在任务列表里就迟早会被切掉,谁知道等我切掉的时候已经掉紫了。”
处理什么问题:
带修树上点对距离查询。这里的“修”不会改变树的形态。
您会说:“我 O(1) 修改,每次查询都 O(n \log n) 跑一遍点分治不香吗?” 这是一种 O(q\cdot n\log n) 的优秀算(bao)法(li)。
抱歉,点分树可以达到 O(q\log n) 的效率。如果算上它上边套的别的数据结构(比如平衡树哇,堆哇),也一般能有 O(q\log^2 n) 的高性能。
思想是什么:
想想您的暴力为什么会有这么大的复杂度。
找重心,回答询问,修改,又找重心,又回答询问,又修改……
看得出,您的做法有不少重复的操作。
尝试优(tou)化(gong)算(jian)法(liao)。
询问和修改我们都不敢偷懒,只能从找重心开刀。
我们发现,因为树的形态始终不变,找到的重心永远都是那几个。
又想到,我们每一次统计答案( \operatorname{calc} ),总是在递归重心时的 \operatorname{solve} 函数里。这是否表明一个重心点,它还能表示一些其他的有关答案的信息呢?
必然是可以的,我们甚至还能用取重心的搜索序建出一棵树来。这棵树就称作点分树。
接下来,我们声称:两个点在原树上的距离为他们的 真实距离 。(区别于点分树上的距离)
我这是一棵树(确信),树上有 6 个顶点。
我取重心 4 作为根,我开一个 tong\_4 装以 4 为根的子树中出现的 点到根的真实距离 情况。 (右边是当前 点分树 的形态)
我取重心 2 为根,距离情况再装桶。
如此往复。最终得到了图上的所有信息。
这些信息是可以在 O(n\log n) 时间内得到的。下面考虑修改:
如果我们要修改原树上 1\ 2 之间的边权,从 val=1 改为 val=2 。哪些桶里装的值会受影响?
大眼观察法, tong\_2 和 tong\_4 会受影响。
可见会受到修改的影响的,是这条边 在点分树上 的祖先们。
我们往下递归找重心时,记录一下每个重心是 从谁递归过来 的,记之为 fa 。(一般点分树的题不用建出真正的点分树形态,比如像这里只要记录其 点分树上 的父亲 fa 即可)。
向上跳 fa ,每跳到一个点,修改相应的数据结构。 (像这里就是修改桶里的值~)
我们珂以保证:这样跳 fa 可以只跳 \log n 次。
原因?
点分治拥有的 \log n 的优秀递归层数,使得点分树的层数也能控制在 \log n 。
而查询更是轻松,只需直接调用数据结构里的信息就可了。
妙到家。
劲爆习题:
模板题: QTREE5 - Query on a tree V
其实不是很板。/kk
修改 :翻转颜色,查询 :给定 u ,求树上距 u 最近白点。
一上来就整点“好康的”。可以充分感受点分树的恶意。(bushi
查询的是最值,那就不是开桶那么简单了。
我们要开堆。
每个点必然要开一个堆,装的是它的 点分树子树 里的点,到它的 真实距离 。(因为是最 小 值,所以开小根堆)
因为有时会有白点变成黑的,无法计入答案,所以要写一个 可删堆 AwA 。
这其实算得上一种小 trick ,下面有放代码的。
那么修改操作即为:
一个点 P 变白了 \rightarrow 跳到其 点分树上 的父亲 FA \rightarrow 往 FA 的堆里塞一个表示 P 到 FA\ 真实距离 的元素 \rightarrow 跳到更高一级的 FA \rightarrow 塞元素 \rightarrow\; \cdots
一个点 P 变黑了 \rightarrow 跳到其 点分树上 的父亲 FA \rightarrow 在 FA 的堆里删去表示 P 到 FA\ 真实距离 的元素 \rightarrow 跳到更高一级的 FA \rightarrow 删元素 \rightarrow\; \cdots
都维护了这么多东西了,那么查询操作就有 手 就 行。我们要查询一个点 P 的最近白点。
扫一遍它在 点分树 上的所有祖先。为什么是点分树?因为一个点的距离信息都保存在了它点分树上祖先的堆里,所以是在点分树上跳祖先。
取出祖先 FA 位置上堆的堆顶,这个堆顶就是所有过 FA 的 真实路径 中最短的一条。
这个堆顶和 P 到 FA 的 真实距离 可以拼起来,形成一个如树上路径 Case\ 1 的两点点距。
不断上跳 FA ,对点距多次取 min 。最终就能得到答案辣!
#include <bits/stdc++.h>
using namespace std;
#define RUN(u) for (int i = head[(u)]; i; i = e[i].next)
#define GI greater<int>
const int MAX = 1e5 + 7;
const int INF = 1e9 + 7;
/*存图组件*/
struct edge
{
int next;
int to;
} e[MAX << 1];
int head[MAX], eid = 0;
void adde(int x, int y)
{
e[++eid].to = y;
e[eid].next = head[x];
head[x] = eid;
}
/*点分治组件*/
int size[MAX], son[MAX], vis[MAX];
int cent, N, Q, SUM;
void get_root(int u, int lst)
{
size[u] = 1;
son[u] = 0;
RUN(u)
{
int v = e[i].to;
if (v == lst || vis[v])
{
continue;
}
get_root(v, u);
size[u] += size[v];
son[u] = max(son[u], size[v]);
}
son[u] = max(son[u], SUM - son[u]);
if (son[u] < son[cent])
{
cent = u;
}
}
int dis[27][MAX], dep[MAX];
//dis:表示某点到其fa的真实距离
//第二维是指该点的编号 第一维是指“这是它的第几级祖先”
//dep:表示该点在点分树上的深度,这决定了它上面有几级祖先。
int fa[MAX];
void getdis(int u, int lst, int stp)
{
dis[stp][u] = dis[stp][lst] + 1;
RUN(u)
{
int v = e[i].to;
if (vis[v] || v == lst)
{
continue;
}
getdis(v, u, stp);
}
}
/*点分树组件*/
void solve(int u, int stp)//stp:遍历到的点分树深度
{
/*点分治板子*/
dep[u] = stp;
vis[u] = 1;
RUN(u)
{
int v = e[i].to;
if (vis[v])
{
continue;
}
dis[stp][u] = 0;
getdis(v, u, stp);
}
RUN(u)
{
int v = e[i].to;
if (vis[v])
{
continue;
}
cent = 0;
son[0] = INF;
SUM = size[v];
get_root(v, u);
get_root(cent, u);
fa[cent] = u;//一个点在点分树上的父亲即是它“从谁递归过来”
solve(cent, stp + 1);
}
}
priority_queue<int, vector<int>, GI> rema[MAX], dele[MAX];
//可删堆,现在还看不出什么高妙,详情见 query
//我们称rema为剩余堆,dele为删除堆
int color[MAX];//颜色
void update(int x)
{
int u = x;
for (int i = dep[x]; i; i--)
{
if (color[x] == 0)
{
rema[u].push(dis[i][x]);
//若原为黑,则现在变为白,加点
}
else
{
dele[u].push(dis[i][x]);
//若原为白,则现在变为黑,删点
}
u = fa[u];//跳fa
}
color[x] = 1 - color[x];
}
int query(int x)
{
int u = x, ans = INF;
for (int i = dep[x]; i; i--)
{
while (!rema[u].empty())
{
if (!dele[u].empty() && dele[u].top() == rema[u].top())
//若一个元素同时出现在剩余堆和删除堆,则这是一个被删除过的元素。
{
dele[u].pop();
rema[u].pop();
//阴阳人滚出优先队列
}
else
{
ans = min(ans, dis[i][x] + rema[u].top());
//反复取min
break;
}
}
u = fa[u];
}
if (ans == INF)
{
return -1;
}
return ans;
}
int main()
{
cin >> N;
for (int i = 1; i <= N - 1; i++)
{
int fr, to;
cin >> fr >> to;
adde(fr, to);
adde(to, fr);
}
solve(1, 1);
cin >> Q;
for (int i = 1; i <= Q; i++)
{
int opt;
cin >> opt;
if (opt == 0)
{
int num;
cin >> num;
update(num);
}
else
{
int num;
cin >> num;
cout << query(num) << endl;
}
}
}冲高端题 :[ZJOI2007]捉迷藏
是ZJOI远古题!
显然那时候浙江省选的毒瘤综合征就已经在潜伏期了。
相比上题,没有了确定的 u ,而是要在全树上查最大值。
上题要考虑的范围那么小,还仅仅卡着复杂度过题,这次有那么多条边要枚举。带毒瘤,爬了爬了。
想想有没有什么“高妙”做法。
全树最大值,所以我们需要开一个全局的大根堆,维护 点分树 上的最大 点对真实距离 。记此堆为 \mathtt{ALL} 。
上道题 “每个点开一个堆,装它的 点分树子树 里的点,到它的 真实距离 ” 的思路依然保留。记这些堆为 \mathtt{subtofa[1...n]}
但仅有一个 \mathtt{subtofa} 堆无法直接维护 \mathtt{ALL} 。我们可以再整一个堆用于过渡。
先更改 \mathtt{subtofa[1...n]} 的定义为:“每个点(称它为 u )开一个堆,装 u 的 点分树子树 里的点,到 u 的父亲的真实距离 ”(差别在于真实距离是到它父亲的)。
再开一个堆表示 “对于一个点 u 在 点分树 中的每个儿子 v ,都把 \mathtt{subtofa[v]} 中最大的一个装进这个堆里”。记这种堆为 \mathtt{fainsub[1...n]} 。
代码中的这句话可以彰显出其关系:
fainsub[u].push(subtofa[cent].top());
//存进subtofa的最大值而关于 \mathtt{fainsub} 和 \mathtt{ALL} ,可以看出 \mathtt{ALL} 里装的东西始终为: 每个 \mathtt{fainsub} 中,堆顶的 两个长度的和 (参考以 Case\ 1 的形式拼接两个长度,以形成一条路径) 。
更新 \mathtt{ALL} 堆的代码实现~
void ins_ALL(int u)
{
if (fainsub[u].size() >= 2)
{
ALL.push(fainsub[u].top() + fainsub[u].second());
//ALL是自定义的“可删堆”类型,second取出的是其第二大的元素
}
}如果您对定义感到疑惑,这里给出一种感性理解(毕竟我也给这道题题解的各种定义看自闭过):\texttt{subtofa} 维护的是纵向的距离最大值, \mathtt{fainsub} 维护的是横向的距离最大值。
给出一张图助于理解:
如果点 u 关灯,则将像上题一样,不断跳 fa ,将 \mathtt{subtofa[u].top()} 加入这个 fa 的 \mathtt{fainsub[fa]} ,再将新的 \mathtt{fainsub[fa]} 装进 \mathtt{ALL} 。
若开灯,则将以上操作改为删除元素。
自认为说的很详尽了。
#include <bits/stdc++.h>
using namespace std;
#define RUN(u) for (int i = head[(u)]; i; i = e[i].next)
#define GI greater<int>
const int MAX = 1e5 + 7;
const int INF = 1e9 + 7;
/*存边组件*/
struct edge
{
int next;
int to;
} e[MAX << 1];
int head[MAX], eid = 0;
int N, Q;
void adde(int x, int y)
{
e[++eid].to = y;
e[eid].next = head[x];
head[x] = eid;
}
/*封装可删堆*/
struct removable_priority_queue
{
priority_queue<int> rema, dele;
void remove(int x)
{
dele.push(x);
}
void push(int x)
{
rema.push(x);
}
int top()
{
while (!rema.empty() && !dele.empty() && dele.top() == rema.top())
{
dele.pop();
rema.pop();
}
return rema.top();
}
int second()
{
int maxx = top();
rema.pop();
int ans = top();
rema.push(maxx);
return ans;
}
int size()
{
return rema.size() - dele.size();
}
} subtofa[MAX], fainsub[MAX], ALL;
/*用 fainsub 更新全局 ALL*/
void del_ALL(int u)
{
if (fainsub[u].size() >= 2)
{
ALL.remove(fainsub[u].top() + fainsub[u].second());
}
}
void ins_ALL(int u)
{
if (fainsub[u].size() >= 2)
{
ALL.push(fainsub[u].top() + fainsub[u].second());
}
}
/*点分治组件*/
int size[MAX], son[MAX];
int cent, SUM;
int vis[MAX];
void getroot(int u, int lst)
{
size[u] = 1;
son[u] = 0;
RUN(u)
{
int v = e[i].to;
if (v == lst || vis[v])
{
continue;
}
getroot(v, u);
size[u] += size[v];
son[u] = max(son[u], size[v]);
}
son[u] = max(son[u], SUM - son[u]);
if (son[u] < son[cent])
{
cent = u;
}
}
int dis[27][MAX];
int color[MAX];
void getdis(int u, int lst, int stp, int root)
{
subtofa[root].push(stp);
RUN(u)
{
int v = e[i].to;
if (vis[v] || v == lst)
{
continue;
}
getdis(v, u, stp + 1, root);
}
}
int fa[MAX];
void solve(int u)
{
vis[u] = 1;
RUN(u)
{
int v = e[i].to;
if (vis[v])
{
continue;
}
cent = 0;
son[0] = INF;
SUM = size[v];
getroot(v, u);
fa[cent] = u;//记录fa
getdis(v, u, 1, cent);
fainsub[u].push(subtofa[cent].top());
//存进subtofa的最大值
solve(cent);
}
fainsub[u].push(0);//可以自己到自己
ins_ALL(u);
}
/*LCA组件(蒟蒻太蔡了打了个倍增)*/
int dep[MAX], lg[MAX];
int father[MAX][27];
void LCA_prework(int u, int lst)
{
dep[u] = dep[lst] + 1;
father[u][0] = lst;
for (int i = 1; i <= 17; i++)
{
father[u][i] = father[father[u][i - 1]][i - 1];
}
for (int i = head[u]; i; i = e[i].next)
{
if (e[i].to == lst)
{
continue;
}
LCA_prework(e[i].to, u);
}
}
int LCA(int x, int y)
{
if (dep[x] < dep[y])
{
swap(x, y);
}
while (dep[x] > dep[y])
{
x = father[x][lg[dep[x] - dep[y]] - 1];
}
if (x == y)
{
return x;
}
for (int i = lg[dep[x]] - 1; i >= 0; i--)
{
if (father[x][i] != father[y][i])
{
x = father[x][i];
y = father[y][i];
}
}
return father[x][0];
}
int dis_on_real(int x, int y)
{
return dep[x] + dep[y] - dep[LCA(x, y)] * 2;
}
/*开灯*/
void turn_on(int u)
{
del_ALL(u);
fainsub[u].remove(0);//首先不能自己到自己了
ins_ALL(u);
for (int now = u; fa[now]; now = fa[now])//跳fa
{
int D = dis_on_real(u, fa[now]);
del_ALL(fa[now]);//先取出第一层
if (subtofa[now].size())
{
fainsub[fa[now]].remove(subtofa[now].top());
//取出第二层
}
subtofa[now].remove(D);//铲除祸根
if (subtofa[now].size())
{
fainsub[fa[now]].push(subtofa[now].top());//放回
}
ins_ALL(fa[now]);//放回
}
}
/*关灯*/
void turn_off(int u)//见上
{
del_ALL(u);
fainsub[u].push(0);
ins_ALL(u);
for (int now = u; fa[now]; now = fa[now])
{
int D = dis_on_real(u, fa[now]);
del_ALL(fa[now]);
if (subtofa[now].size())
{
fainsub[fa[now]].remove(subtofa[now].top());
}
subtofa[now].push(D);
if (subtofa[now].size())
{
fainsub[fa[now]].push(subtofa[now].top());
}
ins_ALL(fa[now]);
}
}
/*多此一举的修改函数*/
void update(int u)
{
if (color[u] == 0)
{
turn_on(u);
}
else
{
turn_off(u);
}
}
int black;
int main()
{
ios::sync_with_stdio(0);
cin >> N;
for (int i = 1; i <= N; i++)
{
lg[i] = lg[i - 1] + (i == (1 << lg[i - 1]));
}
for (int i = 1; i <= N - 1; i++)
{
int fr, to;
cin >> fr >> to;
adde(fr, to);
adde(to, fr);
}
LCA_prework(1, 0);
SUM = N;
cent = 0;
son[0] = INF;
getroot(1, 0);
solve(cent);
black = N;
cin >> Q;
for (int i = 1; i <= Q; i++)
{
char opt;
cin >> opt;
if (opt == 'G')
{
if (black == 0)
{
cout << -1 << "\n";
continue;
}
if (black == 1)
{
cout << 0 << "\n";
continue;
}
cout << ALL.top() << "\n";
}
else
{
int w;
cin >> w;
if (color[w] == 1)
{
black++;
}
else
{
black--;
}
update(w);
color[w] = 1 - color[w];
}
}
}有三倍经验 AwA :Qtree4 (这题要小心带边权) QTREE4 - Query on a tree IV (我至今没卡完的常)
阴间题: [WC2014]紫荆花之恋
我 不 会(逃
以后来填坑。
无旋 treap
“这个splay就是逊啦!”
早就学过 splay ,但每次敲完都会出锅,总是要对着板子全文比较。
导致给了窝一个刻板印象:平衡树=不行 。
平衡树什么时候时候才能站起来?气抖冷。
直到窝开始盘算着学无旋 treap 。
这是什么:
一种基于分裂合并操作的 treap ,可以跑持久化,但不能很轻松地维护 LCT 。
最重要的是,它很短。而且板子极为好背,针不戳。
思想是什么:
前置知识:知道普通 treap 的形态与性质。
考虑一棵 treap ,他在 val 的维度上维持二叉搜索树的性质,在 prio 维度上维持堆的性质。如下图:
即:
其中序遍历为原序列的 按 val 的有序排列 (二叉搜索树的性质)
对于任何一棵子树,都满足 根的 prio 值大于儿子的 prio (堆的性质)
无旋 treap 的特性:
(接下来的叙述将会围绕着如何使无旋 treap 完成 ”加点、删点、查第 k 大、查排名、查前驱后继“ 来展开!)
人群当中突然钻出来一个奆佬,表示发现了一个二叉搜索树的巧妙性质:
以任意一个 在值域当中的数 val 为分割线,一定能将二叉搜索树分成 “小于等于 val ” 与 “大于 val ” 两部分,且这两部分分开来看也各是一棵二叉搜索树。
还是以原来这棵树为例,如果我们从 val=5 切割:
(更正:右半边 val=1 的结点对应标号应为 4 )
我们发现这一个数就把他分( \operatorname{split} )成了两棵二叉搜索树。
我们借助这一性质,来尝试进行一些操作。
加点:
首先考虑,我们直接加点时,往往只能做到把新点挂在外围。然后再经过胡乱操作( 如 splay 中的 \operatorname{rotate} )保送这个新点到该去的位置。
而无旋 treap 则没有这样的烦恼。
倘若我们要加一个 val=2 的点,我们先把原树按 2 \operatorname{split} 出了 L,R 两棵子树。
这时,我们创造一个游离的结点,保存新元素的值。
如此实现:
struct node
{
int son[2];//左右儿子
int val;//val值
int prio;//随机赋给其的prio值,用于建出一个堆
int size;//以之为根的子树大小
} T[MAX];
#define ls(a) T[(a)].son[0]
#define rs(a) T[(a)].son[1]//宏定义
int ROOT, cnt = 0;//根、当前点的编号
void add(int x)//造一个游离点
{
T[++cnt].size = 1;
T[cnt].val = x;
T[cnt].prio = rand();
ls(cnt) = rs(cnt) = 0;//各种初始化
}此时,我们发现原来的平衡树,它裂了(悲),但问题不大,我们可以想办法合并( \operatorname{merge} )。
因为我们合并以后,需要仍然保持 treap 的性质。故应判断需要合并的两棵树的 树根的 prio 值的大小关系 。谁的 prio 的更小,谁就挂在对方的下面。(怪)
这样我们先将这个游离点与左树 \operatorname{merge} ,再将左树与右树 \operatorname{merge} 即可~
(图被我弄丢了ToT ,或许可以使用上面那张图格物致知?)
那么,当我们在加点过程中,把一个不平衡的二叉搜索树 裂开来 ,再以一种平衡的方式 合并 回去,就能起到“制衡”的作用辣!AwA
该部分代码如下:
void push_up(int p)//更新size
{
T[p].size = T[ls(p)].size + T[rs(p)].size + 1;
}
void split(int p, int x, int &L, int &R)
//p,x:当前递归到的点、需要加的值
//&L,&R:传进来两个地址来把最后分出的L,R树的根结点编号运出去
{
if (!p)//递归边界
{
L = 0;
R = 0;
return;
}
if (T[p].val <= x)//判断条件,分裂(背板即可)
{
L = p;
split(rs(p), x, rs(p), R);
}
else
{
R = p;
split(ls(p), x, L, ls(p));
}
push_up(p);
}
int merge(int Lroot, int Rroot)//合并的左右树根
{
if (!Lroot)
{
return Rroot;
}
if (!Rroot)
{
return Lroot;
}//倘若另一边为空,则不用和空气贴贴了,直接返回
if (T[Lroot].prio < T[Rroot].prio)//否则判断谁在下面
{
rs(Lroot) = merge(rs(Lroot), Rroot);
//返回的值是两树合并后的大树的树根
push_up(Lroot);
return Lroot;
}
else
{
ls(Rroot) = merge(Lroot, ls(Rroot));
push_up(Rroot);
return Rroot;
}
}
void insert(int x)
{
int l, r;
split(ROOT, x, l, r);//先裂开来
add(x);//创造游离点
ROOT = merge(merge(l, cnt), r);
//先合并左树和新点,再合并左树和右树
}删点:
不会真的有人删点是去把目标结点清空的吧,不会吧不会吧。
可无旋 $treap$ 之所以叫“无旋”,就是因为它没有旋转的操作。
我们充分利用无旋 $treap$ 的特性,大力将要删的结点 $u$ 从全树上 $\operatorname{split}$ 出来,再将 **除去 $u$ 的剩余几部分** 大力 $\operatorname{merge}$ 回去。最终就能收获一个不带 $u$ 的新树辣!
图示如下 $AwA$ :(假设我们现在要删值为 $x=6$ 的点)
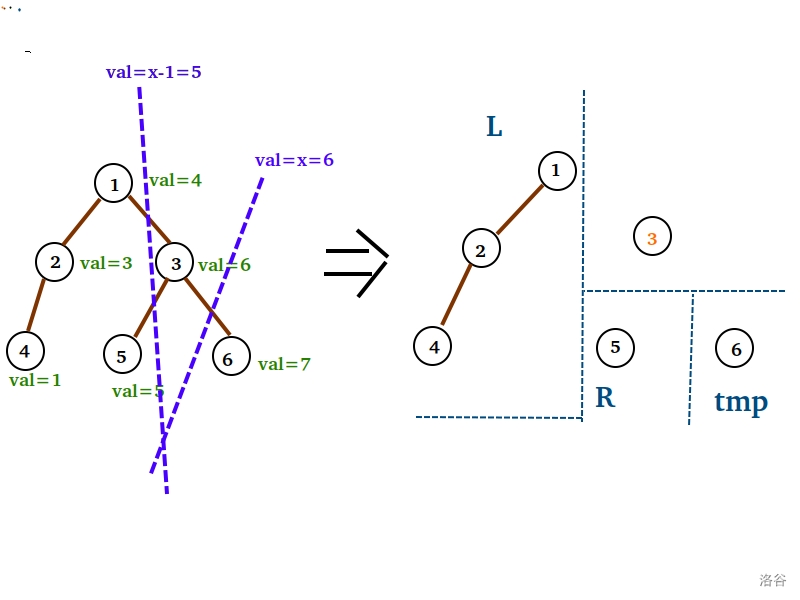
先裂开来。再排除 $val=x=6$ 的 $3$ 号点,进行如此合并。
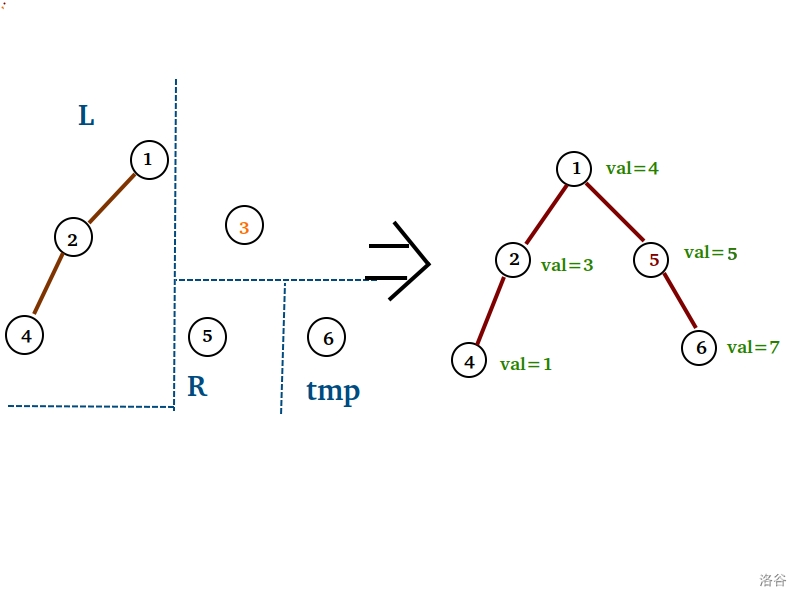
这部分的代码实现~
```cpp
void erase(int x)
{
int l, r, tmp;
split(ROOT, x, l, tmp);//先将大于x的部分split出来
split(l, x - 1, l, r);//再将小于x的部分split出来
r = merge(ls(r), rs(r));//为防止R的儿子分崩离析,先合并其儿子
ROOT = merge(merge(l, r), tmp);//按顺序合并
}
```
**为什么只用担心 $R$ 的儿子分崩离析?**
因为他的位置很尴尬,他的左儿子可能会被 $x-1$ 的一刀砍断,右儿子可能会被 $x$ 的一刀砍断。(惨 R 惨)
------------
###### 查第 $k$ 大:
因为这是一棵二叉搜索树,所以用脚想都知道一种可行的方法是中序遍历再查。
而且这种方法复杂度还不赖,甚至有 $O(n)$ !(~~暴力之耻~~)
可是你清醒一点,这是一棵平衡树,他的常数不可谓不小。
再者说之后我们的 $pre$ 和 $nxt$ 函数也要用到它(好像有点剧透?)。
我们希望找到一个复杂度优秀的做法。
我们突然想到,我们 $treap$ 的结点信息里,似乎还保存了一个 $size$ 变量。
$\color{black}\mathtt{D}\color{red}\mathtt{Pair}$ 神说过,优化的第二种方式是 **“可并的操作一起处理” 。**
如果我们明明知道左子树里根本没有 $k$ 这么多个元素,也就不可能存在第 $k$ 大的数。那我们凭什么往里面去递归。
这 **给** 了我们一个启发,根据 $size$ 确定递归范围,逐层找到对应位置。
代码实现如下~
```cpp
int getkth(int p, int K)
{
if (K <= T[ls(p)].size)//如果左子树里的的确确有k这么多的元素
{
return getkth(ls(p), K);//就找这其中的第k个
}
if (K == T[ls(p)].size + 1)//如果发现当前就是你要找的那个
{
return p;//返回
}
return getkth(rs(p), K - T[ls(p)].size - 1);
//否则,左子树把k消耗掉了T[ls(p)].size,自己又消耗掉了1
//则在右子树里查第k - T[ls(p)].size - 1位
}
```
------------
###### 获取元素排名:
这一操作用的不多,随便口胡一下(~~逃~~
我们把一个元素以它的 $val$ 值 $split$ 出来。这时人群当中钻出来一个 $dalao$ ,他说:“我知道了,$L$ 树里的元素全都是比它小的!”
u1s1,qs。
有 $T[ls(p)].size$ 这么多的元素比它小,那么显而易见地,这个元素的排名就是 $T[ls(p)].size+1$ 。
别忘了 $\operatorname{merge}$ 回去。
代码如下~
```cpp
int getrank(int p, int K)
{
int l, r;
split(ROOT, K - 1, l, r);//按k-1 split出来
int ans = T[l].size + 1;//获得排名
ROOT = merge(l, r);//合并回去
return ans;//返回值
}
```
------------
###### 查前驱:
我们之前提(~~剧透~~)到查前驱也是要用到查 $k$ 小值这一操作,想必各位一定已经YY出了做法了吧。
实则很简单,我们查前驱,实则就是要找小于 $x$ 的元素中,最大的一个,我们把小于 $x$ 的部分 $\operatorname{split}$ 出来后,取出这一部分的第 $T[L].size$ 位元素就可了。
别忘了 $\operatorname{merge}$ 回去。
```cpp
int pre(int x)
{
int l, r;
split(ROOT, x - 1, l, r);//将小于x的部分分离出来
int ans = T[getkth(l, T[l].size)].val;//取第T[l].size位
ROOT = merge(l, r);
return ans;
}
```
------------
###### 查后缀:
后缀与前驱同理,不多加赘述:
```cpp
int nxt(int K)
{
int l, r;
split(ROOT, K, l, r);//将大于x的部分分离出来
int ans = T[getkth(r, 1)].val;//取第1位
ROOT = merge(l, r);
return ans;
}
```
-----
得,这就是无旋 $treap$ 吗,i了i了。
------------
#### 劲爆习题:
**模板题**:[【模板】普通平衡树](https://www.luogu.com.cn/problem/P3369)
板子题首当其 **冲** !
要求的就是之前的六个操作,码一遍就 VAN 事了。
```cpp
#include <bits/stdc++.h>
using namespace std;
#define ls(a) T[(a)].son[0]
#define rs(a) T[(a)].son[1]
const int MAX = 1e5 + 7;
int N, ROOT, cnt = 0;
struct node
{
int son[2];
int fa;
int val;
int prio;
int size;
} T[MAX];
/*创造新点*/
void add(int x)
{
cnt++;
T[cnt].size = 1;
T[cnt].val = x;
T[cnt].prio = rand();
ls(cnt) = rs(cnt) = 0;
}
/*整合子树信息*/
void push_up(int p)
{
T[p].size = T[ls(p)].size + T[rs(p)].size + 1;
}
/*分裂*/
void split(int p, int x, int &L, int &R)
{
if (!p)
{
L = 0;
R = 0;
return;
}
if (T[p].val <= x)
{
L = p;
split(rs(p), x, rs(p), R);
}
else
{
R = p;
split(ls(p), x, L, ls(p));
}
push_up(p);
}
/*合并*/
int merge(int Lroot, int Rroot)
{
if (!Lroot)
{
return Rroot;
}
if (!Rroot)
{
return Lroot;
}
if (T[Lroot].prio < T[Rroot].prio)
{
rs(Lroot) = merge(rs(Lroot), Rroot);
push_up(Lroot);
return Lroot;
}
else
{
ls(Rroot) = merge(Lroot, ls(Rroot));
push_up(Rroot);
return Rroot;
}
}
/*插入操作*/
void insert(int x)
{
int l, r;
split(ROOT, x, l, r);
add(x);
ROOT = merge(merge(l, cnt), r);
}
/*删除操作*/
void erase(int x)
{
int l, r, p;
split(ROOT, x, l, p);
split(l, x - 1, l, r);
r = merge(ls(r), rs(r));
ROOT = merge(merge(l, r), p);
}
/*查第K大*/
int getkth(int p, int K)
{
if (K <= T[ls(p)].size)
{
return getkth(ls(p), K);
}
if (K == T[ls(p)].size + 1)
{
return p;
}
return getkth(rs(p), K - T[ls(p)].size - 1);
}
/*获取排名*/
int getrank(int p, int K)
{
int l, r;
split(ROOT, K - 1, l, r);
int ans = T[l].size + 1;
ROOT = merge(l, r);
return ans;
}
/*获取前驱*/
int pre(int K)
{
int l, r;
split(ROOT, K - 1, l, r);
int ans = T[getkth(l, T[l].size)].val;
ROOT = merge(l, r);
return ans;
}
/*获取后继*/
int nxt(int K)
{
int l, r;
split(ROOT, K, l, r);
int ans = T[getkth(r, 1)].val;
ROOT = merge(l, r);
return ans;
}
int main()
{
srand(20050418);//窝npy的生日ww
int Q;
cin >> Q;
while (Q--)
{
int opt, num;
cin >> opt;
if (opt == 1)
{
cin >> num;
insert(num);
}
if (opt == 2)
{
cin >> num;
erase(num);
}
if (opt == 3)
{
cin >> num;
cout << getrank(ROOT, num) << endl;
}
if (opt == 4)
{
cin >> num;
cout << T[getkth(ROOT, num)].val << endl;
}
if (opt == 5)
{
cin >> num;
cout << pre(num) << endl;
}
if (opt == 6)
{
cin >> num;
cout << nxt(num) << endl;
}
}
}
```
--------
**EX-模板题** :[【模板】文艺平衡树](https://www.luogu.com.cn/problem/P3391)
CSP到了,我向佛祖许愿,希望我的平衡树能实现区间翻转。
佛说:“我的正解是 $splay$ ,那你这在无旋 $treap$ 上如何实现?”
我说:“无旋 $treap$ 的区间处理能力之强。它可以用两次 $\operatorname{split}$ 轻松取出一段区间。”
~~“ splay 做得到吗?”(拉狗行为)~~
佛说:“你翻转了区间,那你这还能叫二叉搜索树吗,你的 $\operatorname{split}$ 不是废了?”
我说:“我的 $\operatorname{split}$ 是按 $size$ 分裂的,这样才可以确定这个区间在原序列上的位置。”(详见代码)
佛说:“不行,单单只是取出一段区间来个 ODT 也能做到,你有什么好说的。”
我说:“那就打一下 $tag$ 。同一区间翻转两次=全部木大。”
佛说:“不行,我这是一棵平衡树,又不是什么线段树。”
我说:“那我就把标记,打在 **分离出来的区间** 的根上,到时候标记下传的时候只需要一番大力 $swap$ 。”
佛说:“不行,我还是不知道怎么打标记。”
我说:“那就来一张图演示一下这一流程。”
(本图不代表最终要操作的序列,但不影响观看)
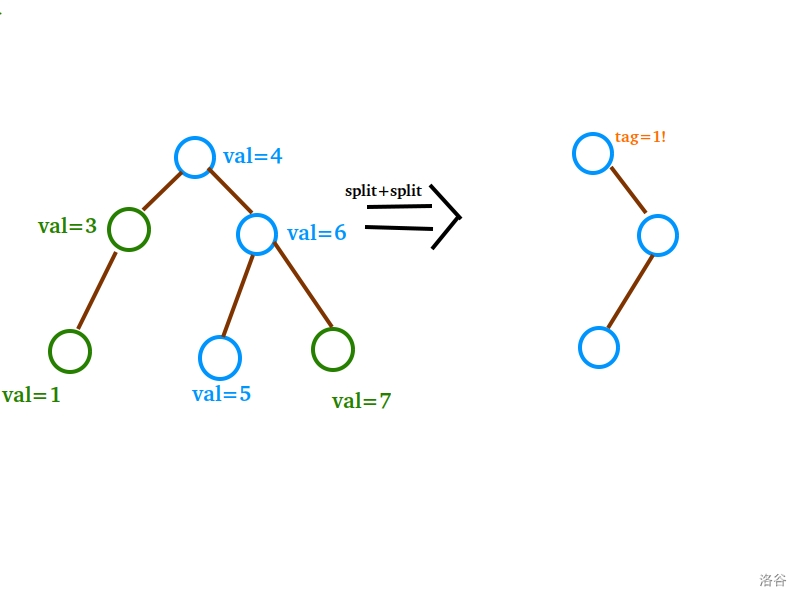
佛说:“不行,我不知道什么时候该下传标记。”
我说:“打过线段树的都知道,不到 **修改** 或 **查询** 的时候是不用 $push\_down$ 的。这里也是如此。”
“修改是没有什么用得上下传标记的地方的,毕竟每次我们分离出一段区间的时候,往往只是在这里打个 $tag$ 。从来没有 **影响过其他地方** 的 $tag$ 。”
“而查询,基于 **『二叉搜索树的中序遍历是它所代表的原序列』** 这一重要思想,我们应该在输出的时候 $push\_down$ 就可以了。
佛说:“不行,那你这 $push\_down$ 函数里面要干什么事情。”
我说:“我们观察到,翻转一个区间,可以看作是一个位置为对称轴,将一段区间 **左右翻转** 得来。”
“知道了这一个条件,我们有了一种强烈的意识,在平衡树上交换一个结点的 **左右两孩子** ,等价于在序列上将一个元素的 **左右两边交换** 。”
佛说:“我不信。”
我说:“手模一下不是有手就行?”
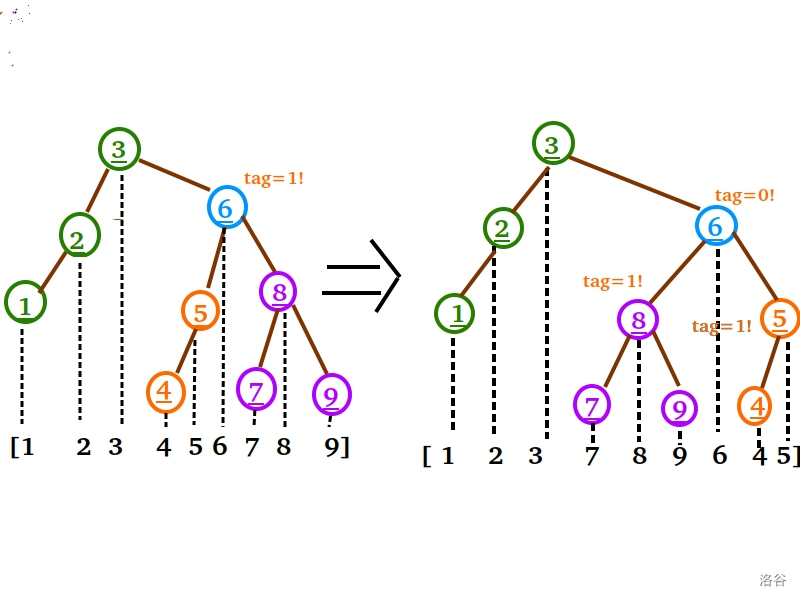
“我们先把6号结点的 $tag$ 先处理了,再把标记往下传,递归进行 ‘**交换左右儿子**’ 这一动作直到叶子结点不就是了。”
佛说:“不行,我是伸手党,我要看代码。”
我说:“彳亍。”
```cpp
void push_down(int p)
{
if (T[p].tag == 0)
{
return;
}
swap(ls(p), rs(p));//交换左右两儿子
T[ls(p)].tag ^= 1;//下传标记
T[rs(p)].tag ^= 1;
T[p].tag = 0;//清空标记
}
```
佛哭了,说:”这样就能AC了。“
```cpp
#include <bits/stdc++.h>
using namespace std;
/*无旋treap基础组件,因码风而异*/
#define ls(a) T[(a)].son[0]
#define rs(a) T[(a)].son[1]
const int MAX = 1e5 + 7;
int ROOT;
struct node
{
int val;
int son[2];
int size;
int tag;
long long prio;
} T[MAX];
void push_up(int p)
{
T[p].size = T[ls(p)].size + T[rs(p)].size + 1;
}
/*下传标记*/
void push_down(int p)
{
if (T[p].tag == 0)
{
return;
}
swap(ls(p), rs(p));
T[ls(p)].tag ^= 1;
T[rs(p)].tag ^= 1;
T[p].tag = 0;
}
int cnt;
/*创造一个新结点*/
void add(int x)
{
T[++cnt].val = x;
T[cnt].prio = rand();
T[cnt].size = 1;
ls(cnt) = rs(cnt) = 0;
}
/*分离*/
void split(int p, int x, int &L, int &R)
{
push_down(p);
if (!x)
{
L = 0;
R = p;
return;
}
if (T[ls(p)].size < x)//这样才能精准定位在原序列上
{
L = p;
split(rs(p), x - T[ls(p)].size - 1, rs(p), R);
}
else
{
R = p;
split(ls(p), x, L, ls(p));
}
push_up(p);
}
/*合并*/
int merge(int Lroot, int Rroot)
{
if (!Lroot || !Rroot)
{
return Rroot + Lroot;
}
push_down(Lroot);
push_down(Rroot);
if (T[Lroot].prio >= T[Rroot].prio)
{
rs(Lroot) = merge(rs(Lroot), Rroot);
push_up(Lroot);
return Lroot;
}
else
{
ls(Rroot) = merge(Lroot, ls(Rroot));
push_up(Rroot);
return Rroot;
}
}
/*插入,其实是用来初始化 treap 用的*/
void insert(int p, int x)
{
int l = 0, r = 0;
split(ROOT, p - 1, l, r);
add(x);
// cout << cnt << endl;
ROOT = merge(merge(l, cnt), r);
}
/*翻转*/
void reverse(int l, int r)
{
int p1 = 0, p2 = 0, p3 = 0;
split(ROOT, r, p1, p2);//右边断开,剩下的装在p1里
split(p1, l - 1, p1, p3);//左边断开,剩下的装在p3里
//这时我们取出的区间,其实就是以p3为根这棵树
T[p3].tag ^= 1;//打tag
ROOT = merge(merge(p1, p3), p2);//合并回去
}
/*中序遍历输出*/
void print(int p)
{
if (p == 0)
{
return;
}
push_down(p);
print(ls(p));
cout << T[p].val << ' ';
print(rs(p));
}
int N, M;
int main()
{
srand(20050418);//窝npy的生日qwq
cin >> N >> M;
for (int i = 1; i <= N; i++)
{
insert(i, i);//初始化
}
while (M--)
{
int l, r;
cin >> l >> r;
reverse(l, r);
}
print(ROOT);
}
```
-----
**次模板题**: [[NOI2004]郁闷的出纳员](https://www.luogu.com.cn/problem/P1486)
一道深刻考验选手对无旋 $treap$ 内层原理的(~~毒瘤~~)好题。
这题要求:1.全局加减 $k$ ,2.删去小于 $val$ 的所有元素 ,3.插入一个元素 , 4.查询第 $k$ 大。
首先一眼发现,因为加减都是全局加减,所以根本没有必要真的加在每一个元素上,随手开个 $delta$ ,表示 **全局的改变量** 。
而剩下与数值有关的,只有一个 “**删去小于 $val$ 的所有元素**” 操作了。
因为我们手上有 $delta$ ,我们可以顺理成章地把这一操作看作 “**删去小于 $val-delta$ 的所有元素**” 。
_(以元素值为参考系(误),元素值增加了delta,可以看作是这个val减小了delta)_
“真正的勇士,敢于面对直接枚举元素的复杂度。”($\times$)
“真正的勇士,敢于面对 TLE 0 。”($\surd$)
你意识到无旋 $treap$ 的 $\operatorname{split}$ 的作用就是将原树分成 “ **小于等于 $val$** ” 与 “ **大于 $val$** ” 两部分。
那我们以 $val-delta$ 分,不就可以让我们分离出来的左树,装的都是小于 $val-delta$ 的元素了?
分离完了以后直接使 **全树的 ROOT 等于右树的根** ,相当于把左树里这些小于 $val$ 的数全部逐入虚空。
这样便可实现删点。
代码如下:
```cpp
#include <bits/stdc++.h>
using namespace std;
#define ls(a) T[(a)].son[0]
#define rs(a) T[(a)].son[1]
const int MAX = 1e5 + 7;
int N, ROOT, cnt = 0, delta = 0;//delta为改变量
struct node
{
int son[2];
int fa;
int val;
int prio;
int size;
} T[MAX];
/*创造新点*/
void add(int x)
{
cnt++;
T[cnt].size = 1;
T[cnt].val = x;
T[cnt].prio = rand();
ls(cnt) = rs(cnt) = 0;
}
/*整合子树信息*/
void push_up(int p)
{
T[p].size = T[ls(p)].size + T[rs(p)].size + 1;
}
/*分裂*/
void split(int p, int x, int &L, int &R)
{
if (!p)
{
L = 0;
R = 0;
return;
}
if (T[p].val <= x)
{
L = p;
split(rs(p), x, rs(p), R);
}
else
{
R = p;
split(ls(p), x, L, ls(p));
}
push_up(p);
}
/*合并*/
int merge(int Lroot, int Rroot)
{
if (!Lroot)
{
return Rroot;
}
if (!Rroot)
{
return Lroot;
}
if (T[Lroot].prio < T[Rroot].prio)
{
rs(Lroot) = merge(rs(Lroot), Rroot);
push_up(Lroot);
return Lroot;
}
else
{
ls(Rroot) = merge(Lroot, ls(Rroot));
push_up(Rroot);
return Rroot;
}
}
/*插入操作*/
void insert(int x)
{
int l, r;
split(ROOT, x, l, r);
add(x);
ROOT = merge(merge(l, cnt), r);
}
/*删除左树*/
int deleteall(int x)
{
int l, r, tmp;
split(ROOT, x - 1, l, r);
int ans = T[l].size;
ROOT = r;//以右树为根
return ans;//返回丢弃的元素数,即T[l].size
}
/*查第k大*/
int getkth(int p, int k)
{
if (T[ls(p)].size >= k)
{
return getkth(ls(p), k);
}
if (T[ls(p)].size + 1 == k)
{
return p;
}
return getkth(rs(p), k - T[ls(p)].size - 1);
}
int main()
{
srand(20050418);
int sumout = 0;//总共被丢掉的人数
int N, LIM;//LIM,下界
cin >> N >> LIM;
for (int i = 1; i <= N; i++)
{
char opt;
cin >> opt;
if (opt == 'I')
{
int num;
cin >> num;
if (num < LIM)
{
continue;
}
insert(num - delta);
//相对地,插入的num也会减小delta
}
if (opt == 'A')
{
int num;
cin >> num;
delta += num;
}
if (opt == 'S')
{
int num;
cin >> num;
delta -= num;
sumout += deleteall(LIM - delta);
//相对地,插入的LIM也会减小delta
}
if (opt == 'F')
{
int num;
cin >> num;
if (T[ROOT].size < num)
{
cout << -1 << "\n";
continue;
}
cout << T[getkth(ROOT, T[ROOT].size - num + 1)].val + delta << endl;
//相应地,查到的第k大也要+delta
}
}
cout << sumout << endl;
}
```
------------
---------
### 网络流基础建模——最大流
这里讲的不是实现,只是一些套路。
------------
$$\color{white}\colorbox{red}{\texttt{FBI WARNING:}}$$
$$\color{white}\colorbox{red}{\texttt{警告:以下内容可能涉及口胡、强迫症、及光敏性癫痫(划)}}$$
$$\color{white}\colorbox{red}{\texttt{请18岁以下儿童在成年人陪同下观看}}$$
------------
都0202年了,不会真有人认为网络流都是套路题吧?
哦是我啊那没事了。
#### 套路一:构建超级源汇:
有的题目,他告诉你谁和谁之间有阿巴阿巴的路径,但硬是不告诉你谁是源,谁是汇。
这时候,朴素的最大流思想可能就会陷入僵局。
但是我们有超级源汇的思想。
我们 **创建一个新点** ,称其为源。
向所有该连的点连边。
汇的思想同理。
建一张图就像这样:

可以看出,这一思想用于处理 **“你……,他……,而我……,我们都有全局的贡献”** 的问题。
下面来看这个命题:
_RUI\_R有了去NOI和APIO的资格,zjjws有了去WC和APIO的资格,而我有了去加里敦参加夏令营的资格,我们都有对XJ的贡献。试问,如果一个人只能去打一场比赛,XJ能收获多少参赛名额。_
一眼看出,这是典型的多源多汇模型。
把每个人和自己能参加的比赛连边,这时相当于是跑一个 **二分图最大匹配** 。
而我们要以网络流的思想解决,则需要 **开一个超级源,向所有人连边,开一个超级汇,让所有比赛向它连边** 。

这里超级源连出去的边容量为1,即 限制了每个人最多 **只能打一场比赛** ,也就是 **从一个人流出的流量最多为1** 。
这启发我们,超级源汇在连边时可以有意无意地起到 **限流** 作用。
##### 劲爆例题:
[飞行员配对方案问题](https://www.luogu.com.cn/problem/P2756)
典型的二分图最大匹配,一边是英国飞行员,一边是外国飞行员,如果俩人能打配合,就在俩人之间连边。
随手像上面那样建一张图。
这时我们发现,外国飞行员也是人,他也只能和一个人进行配对。
~~**外国飞行员** 使用分身术,出现了一个新的 **外国飞行员**~~
所有右边的点向超级汇的连边,容量改为 $1$ 。
这样我们就建出了一张图,在这张图上跑一个最大流就珂以了。
代码如下:
```cpp
#include <bits/stdc++.h>
using namespace std;
/*dinic组件*/
#define int long long
const int MAX = 107;
const int INF = 1e18;
int N, M;
struct edge
{
int next, to, val;
} e[MAX * MAX << 1];
int head[MAX], eid = 1;
void adde(int x, int y, int w)
{
e[++eid].next = head[x];
e[eid].to = y;
e[eid].val = w;
head[x] = eid;
}
int S, T;
int dep[MAX];
int flag = 0;
queue<int> q;
#define RUN(u) for (int i = head[(u)]; i; i = e[i].next)
void bfs()
{
memset(dep, 0, sizeof(dep));
dep[S] = 1;
while (!q.empty())
{
q.pop();
}
q.push(S);
while (!q.empty())
{
int u = q.front();
q.pop();
RUN(u)
{
int v = e[i].to;
if (dep[v] || e[i].val == 0)
{
continue;
}
dep[v] = dep[u] + 1;
q.push(v);
}
}
if (dep[T])
{
flag = 1;
}
}
int dfs(int u, int in)
{
if (u == T)
{
return in;
}
int out = 0;
RUN(u)
{
int v = e[i].to;
if (dep[v] != dep[u] + 1 || e[i].val == 0)
{
continue;
}
int tmp = dfs(v, min(in, e[i].val));
e[i].val -= tmp;
e[i ^ 1].val += tmp;
in -= tmp;
out += tmp;
}
if (out == 0)
{
dep[u] = 0;
}
return out;
}
signed main()
{
int num;
cin >> N >> num;
int fr, to;
S = 0;//超级源定为0号
T = num + 1;//超级汇定为num+1号
/*反正只要是个用不上的点就可以了*/
while (cin >> fr >> to && fr != -1 && to != -1)
{
adde(fr, to, 1);//能配合的俩人连一条边
adde(to, fr, 0);
}
for (int i = 1; i <= N; i++)
{
adde(S, i, 1);//超级源向英国飞行员连边
adde(i, S, 0);
}
for (int i = N + 1; i <= num; i++)
{
adde(i, T, 1);//外国飞行员向超级汇连边
adde(T, i, 0);
}
int ans = 0;
/*奇怪的dinic,写法因人而异*/
while (1)
{
flag = 0;
bfs();
if (flag == 0)
{
break;
}
ans += dfs(S, INF);
}
cout << ans << endl;
for (int i = 2; i <= eid; i++, i++)
{
if (e[i].to != S && e[i ^ 1].to != S && e[i].to != T && e[i].to != T)
//输出方案
//这里的做法是遍历每一条边,查他是否有残量
{
if (e[i ^ 1].val)
{
cout << e[i ^ 1].to << ' ' << e[i].to << endl;
}
}
}
}
```
-------
#### 套路二:最大流改最小割:
~~窝非常擅长鸽。~~
有的题目,他告诉你选了阿巴阿巴就不能选阿巴阿巴。
这时候,朴素的最大流思想可能就会陷入僵局。
但是神仙们证出了最大流等于最小割。
这个问题就转化成了,我 **放弃选一些东西,使我剩下的收益最大** 。
考虑全图中从源点到汇点的一条路径,假设这条路径是由 **好几段拼成** 的。
我想把它割断至无法通流,则必然是割断其中的 **某一段** 。这个“割断”的过程,实则就是相当于 **放弃了这一段的收益** 。
而这条路径上的其它几段得以保留,所以我能获得剩下的这些收益。

这时,存在两条路径从源点通往汇点的路径,我们要把他们割断,一种可行的做法是割断 $value_{\ 5}$ 使剩下4个 $value$ 得以保留。
当然,还存在一种做法是割断 $value_1,value_3$ 使剩下三个得以保留。
此外,在有的题目中,有的利益是固定利益,是无法丢弃的,这时,我们就可以将这条边的容量设为 **INF** 。
可以看出,最小割模型非常善于处理 “**可以……,但是你得……,这一切值得吗?**”的问题。
下面来看这个命题:
_“我告诉你,但是你得跟我搞姬,这一切值得吗?”_
我们可以看出这里存在一个约束关系, “ **我可以得到题解,但是我有翻车的危险,即‘失去了安全’** ”。
那么很显然我们可以建出一张图,像这样:

~~颜色好评~~,如果我们选择了题解,那么我们就会失去开车的安全;反之同理。
##### 劲爆例题:
[方格取数问题](https://www.luogu.com.cn/problem/P2774)
首先,一眼看出模型,“我可以选这个点,但是我就选不了周围这些点了,这一切值得吗?”。
那么我们随便挑出两个相邻的方格,都可以建出这样的图。
表示要么选 $val_1$ ,要么选 $val_2$ 。
如果我们对于每一个点建一张如上例的图,最终的成品就是这个玩意。

这时我们发现,这张图根本没有源和汇。/jk
但是我们的内心毫无波澜,甚至一眼出了 **超级源汇** 的思想。
可超级源汇的模型也不是用脚造的,我们需要决定 **谁去连源,谁去连汇** 。
想起了之前飞行员配对的做法,我们可以把这些点分出一张 **二分图** 。
二分图的要求是同一部分内 **无连边** 。正难则反,什么点之间有连边?显然是相邻的点。
那么,无连边的部分,必然是那些不相邻的。
这时,我们就可以用黑白染色的方式,建出如下的图。

此时,随便挑出一条路径来,依然满足 **最小割** 的样式,可以在这上面跑最大流,来求出这一 **最小的舍弃价值** 。
而我们收获的价值,就是 **所有价值总和-舍弃的价值** 。
代码如下:
```cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int MAX = 1e5 + 7;
const int INF = 1e18;
/*dinic组件*/
struct edge
{
int next, to;
int val;
} e[MAX << 1];
int head[MAX], eid = 1;
void adde(int x, int y, int w)
{
e[++eid].next = head[x];
e[eid].to = y;
e[eid].val = w;
head[x] = eid;
}
int dep[MAX];
int flag = 0;
queue<int> q;
int S, T;
#define RUN(u) for (int i = head[u]; i; i = e[i].next)
void bfs()
{
memset(dep, 0, sizeof(dep));
dep[S] = 1;
while (!q.empty())
{
q.pop();
}
q.push(S);
while (!q.empty())
{
int u = q.front();
q.pop();
RUN(u)
{
int v = e[i].to;
if (e[i].val == 0 || dep[v])
{
continue;
}
dep[v] = dep[u] + 1;
q.push(v);
}
}
if (dep[T])
{
flag = 1;
}
}
int dfs(int u, int in)
{
if (u == T)
{
return in;
}
int out = 0;
RUN(u)
{
int v = e[i].to;
if (e[i].val == 0 || dep[v] != dep[u] + 1)
{
continue;
}
int tmp = dfs(v, min(in, e[i].val));
if (in == 0)
{
return out;
}
e[i].val -= tmp;
e[i ^ 1].val += tmp;
in -= tmp;
out += tmp;
}
if (out == 0)
{
dep[u] = 0;
}
return out;
}
int M, N;
int idx(int x, int y)//获取一个方格的编号
{
return (x - 1) * N + y;
}
signed main()
{
cin >> M >> N;//这道题对N,M的定义是和常识相反的
//申必题(bushi
int sum = 0;
S = 0, T = 107 * 107 + 1;
for (int i = 1; i <= M; i++)
{
for (int j = 1; j <= N; j++)
{
int num;
cin >> num;
sum += num;
if ((i + j) & 1)//若行+列=奇则染白,连源点
{
adde(S, idx(i, j), num);
adde(idx(i, j), S, 0);
/*向上下左右四个方向连边*/
if (i > 1)
{
adde(idx(i, j), idx(i - 1, j), INF);
adde(idx(i - 1, j), idx(i, j), 0);
}
if (i < M)
{
adde(idx(i, j), idx(i + 1, j), INF);
adde(idx(i + 1, j), idx(i, j), 0);
}
if (j > 1)
{
adde(idx(i, j), idx(i, j - 1), INF);
adde(idx(i, j - 1), idx(i, j), 0);
}
if (j < N)
{
adde(idx(i, j), idx(i, j + 1), INF);
adde(idx(i, j + 1), idx(i, j), 0);
}
}
else//若行+列=偶则染黑,连汇点
{
adde(idx(i, j), T, num);
adde(T, idx(i, j), 0);
}
}
}
int ans = 0;
while (1)
{
flag = 0;
bfs();
if (flag == 0)
{
break;
}
ans += dfs(S, INF);
}
cout << sum - ans << endl;//收益为总价值-割
}
```
-----
#### 套路二-进阶:其他黑白染色模型:
上文的方格取数问题,可以归为一种黑白染色模型中的典型。
而解决这种问题,其要义在于构建一种可行的方式,将所有玩意分成两堆,使得任何 **黑点与白点之间都没有直接连边** 。
听上去很 $simple$ ,实际上的确很 $naive$ 。
就随便挑一道题来看叭~
_以下只阐述如何染色,其他实现细节在此不提_
- [骑士共存问题](https://www.luogu.com.cn/problem/P3355)
就用题目上的原图好了。
我们发现 $S$ 在一个黄点,而他的下一步必然是一个红点。(由图可知)
那么我们像方格取数一样,按 **(行+列)的奇偶性** 黑白染色即可。
甚至还能白嫖双倍经验 [](https://www.luogu.com.cn/problem/P4304) 。
\
那个表情是超链接……
- [长脖子鹿放置](https://www.luogu.com.cn/problem/P5030)
长脖子鹿不会被别马腿因为长脖子鹿只有鹿腿哈哈哈哈哈哈哈
~~其实一点也不好笑~~
这道题面里还是有图,我们还是征用题面里的图。
可以看到这里,一个白点会跳到另一个白点上。我们之前(行+列)奇偶性染色法就不行了。
但我们会想出新方法切了这道题。
因为长脖子鹿跳一下是 $2\times 4$ 的,我们发现,行和列加的都是偶数, **不影响其奇偶性** 。
也就是说,奇行和偶行之间不会有连边。
所以我们将 **奇行染黑,偶行染白** 即可。
- [王者之剑](https://www.luogu.com.cn/problem/P4474)
高质量好题/se/se/se(指题面
王固然是天下第一,但是这道题出题人也是脑洞真的大。
我们看见,每隔两秒周围四个地方的宝石都会消失。而这两秒之内我们能干什么,一秒踩在一块有宝石的砖上吸走了宝石,下一秒在一块空砖上赶路前往下一个有宝石的地方。
也就是说,我们吸走了一个地方的宝石, **周围四个位置** 都是必然拿不到了的。
然后,就变成方格取数问题了???
我直接震惊。
- 有一道叫 [[国家集训队]部落战争](https://www.luogu.com.cn/problem/P2172) 的题,看上去很像黑白染色,事实上他是最小路径覆盖问题。我们之后会提到。
--------
#### 套路一+套路二=套路三:最大权闭合子图模型
“有的题目,他告诉你必须得选阿巴阿巴才能选阿巴阿巴。有时候选阿巴阿巴可能带来负收益。”
这和套路二的最小割模型没有什么区别,如果你是~~语文王子~~,你会发现上面这句话其实和套路二表达的是同一个意思。
只不过让人以为这里仿佛有负边权,然后自闭。
我们换一种说法:对于一个正收益的东西,我们要么 **得到这个价值** ,要么 **省下“得到这个价值”所需要的钱** 。
由此一来,最小割的思想就呼之欲出力。

即:要么获得价值 $value$ ,要么赚回花费 $cost$ 。
由于一个正收益的物品,可能需要很多种的 **前置花费** ,同时,一个负收益的物品可能同时成为很多物品的 **前置花费** 。
所以我们常常会用到超级源汇的思想 $qwq$ 。
不难看出,最大权闭合子图模型适合解决 **“tyy讲题”** 类型的题。
(~~生动比喻了有一大堆前置知识的数论 **浅** 谈~~)
我们来看下面这个命题:
> tyy在讲课,今天他要讲的是杜教筛和min25,其中,杜教筛需要莫反和积性函数的前置知识,min25需要多项式和积性函数的前置知识,学这些前置知识需要你爆掉一定的肝,但是学一个新科技筛法又可以恢复一定的肝,求自己最大收益。
一眼发现有 “前置知识” 这一 **有 趣** 的玩意。
我们把杜教筛单独拉出来看,有下面的最小割模型:

(~~颜色好评~~)
表示我们要么去学杜教筛 $val_{mifafa}$ ,要么省下 $cost_{mobius}+cost_{multi}$ 的花费。
而放之全图就像这样:
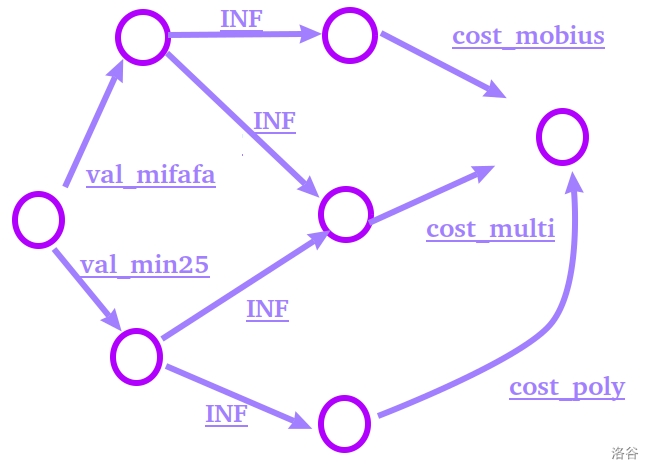
~~迫真英语翻译。~~
这样,我们就可以跑出全图的最小割辣。
但是,我们此时不能直接用总价值减去最小割来求解。
我们此前称学习前置知识的价值,是 **我们省下了多少肝** 。
可我们什么也不学,他又不会白送我们这些肝。换言之,这些肝本就不是我们应得的。
我们本该得的,是学这些筛法所收获的科技知识。
~~明明是你自己要偷懒护肝的。~~
所以我们应该用所有筛法的收益之和,减去最小割,这才是我们最终的答案。
$$ans=val_{mifafa}+val_{min25}-smallest\_cut$$
##### 劲爆例题:
[拍照](https://www.luogu.com.cn/problem/P3410)
一眼看出,我可以获得拍一张照的价值,但是我有带几个人的前置条件。
这很容易就转化为了 **最大权闭合子图** 的模型。
用脚也可以造出同上例一样的图。
(其实用本题样例建出来的图和上一张图是一模一样的。)
然后按部就班做就VAN事了。
```cpp
#include <bits/stdc++.h>
using namespace std;
/*dinic组件*/
#define int long long
const int MAX = 107 * 107;
const int INF = 1e18;
struct edge
{
int to, next, val;
} e[MAX];
int head[MAX], eid = 1;
void adde(int x, int y, int w)
{
e[++eid].to = y;
e[eid].next = head[x];
e[eid].val = w;
head[x] = eid;
}
int dep[MAX];
queue<int> q;
int flag = 0;
int S, T;
#define RUN(u) for (int i = head[(u)]; i; i = e[i].next)
void bfs()
{
memset(dep, 0, sizeof(dep));
dep[S] = 1;
while (!q.empty())
{
q.pop();
}
q.push(S);
while (!q.empty())
{
int u = q.front();
q.pop();
RUN(u)
{
int v = e[i].to;
if (dep[v] || !e[i].val)
{
continue;
}
dep[v] = dep[u] + 1;
q.push(v);
}
}
if (dep[T])
{
flag = 1;
}
}
int N, M;
int dfs(int u, int in)
{
if (u == T)
{
return in;
}
int out = 0;
RUN(u)
{
int v = e[i].to;
if (dep[v] != dep[u] + 1 || e[i].val == 0)
{
continue;
}
int tmp = dfs(v, min(in, e[i].val));
e[i].val -= tmp;
e[i ^ 1].val += tmp;
in -= tmp;
out += tmp;
}
if (out == 0)
{
dep[u] = 0;
}
return out;
}
signed main()
{
cin >> M >> N;
S = 0, T = N + M + 1;//超级源汇
int sum = 0;//正收益之和
for (int i = 1; i <= M; i++)
{
int num;
cin >> num;//照片价值,由源点连边,累加进sum
sum += num;
int l;
adde(S, i, num);
adde(i, S, 0);
while (cin >> l && l)
{
adde(i, l + M, INF);//向前置条件连边
adde(l + M, i, 0);
}
}
for (int i = 1; i <= N; i++)
{
int num;
cin >> num;//前置花费,向汇点连边
adde(i + M, T, num);
adde(T, i + M, 0);
}
int ans = 0;
while (1)
{
flag = 0;
bfs();
if (flag == 0)
{
break;
}
ans += dfs(S, INF);
}
cout << sum - ans << endl;//跑最小割,出结果
}
```
------------
#### 套路四:拆点
“有的题目,他告诉你他要最大收益,但是一个物品只能用阿巴阿巴次。或者他要最小割,但是割的是点,不是边。”
这是,朴素的最大流/最小割就会陷入僵局。
但是拆点是一个好 办 法。
拆点的要义是:把一个点拆成 **入点** 和 **出点** 两个点,在这两个点之间连上一条 **一定容量 $limit$** 的边。
这样,任何时候,通过这个点的流量都只会控制在 $limit$ 之内。
老百度网盘了
具化到图上,如果我们需要控制通过一个点的流量永远不超过 $limit$ ,则有:

$in$ 和 $out$ 都是从同一个点上拆出来的,我们让通过这个点的流量不超过 $limit$ ,实际上就可以把 $in$ 和 $out$ 之间这条边的容量限为 $limit$ 。
不难看出,拆点模型适合处理“~~购买超级会员享受8倍速度~~” 的百度云 **限流** 行为。
来看下面这个命题:
> XJ地形可以简化成一张有向无环图。在结点处,会站有值周班同学检查。此时,在他面前跑过的人 **禁止超过** $W_i$ 。现在给出每个结点处的检查情况,试求最多有多少学生能在去食堂的路上跑步。
[原题链接【12:20】(还没有数据)](https://www.luogu.com.cn/problem/U141285)
很显然,这里有明显的限流现象。( ~~指站在一旁看着高一学生 rush~~ )
从一个检查点到另一个检查点是随便你怎么跑的,~~从XJ中学12:20时的情况便可知晓~~。
言外之意是, **边** 上的限流为 $inf$ 。
而对于一个点上的限流,我们把一个点拆成一个出点和一个入点,两点之间连长度为 **人数限制** 的一条边。
这样,我们就能建出这样一张图:

在这张图上,我们就可以做到通过每个检查点的人数不超过 $limit$ 人。
可以注意到的是,**图上源连的是入点,汇连的是出点,前一个点的出点连的是后一个点的入点**。
而这张图上的最大流,就是本题的答案。
#### 劲爆习题:
[[USACO5.4]奶牛的电信Telecowmunication](https://www.luogu.com.cn/problem/P1345)
之前是拆点求最大流,而现在是拆点求最小割。
不能割边,则把所有边的边权设成 $inf$ ,这是无可厚非的。
因为我们割的是点,而点在网络流上不好处理,所以我们把一个点拆成两个点,两点之间连容量为 $1$ 的边。
**为什么连边权为 $1$ 呢?**
我们割一条这种边,相当于我们拆了一台电脑。(可怜的 FarmerJohn /dk)
而题目要求的是拆电脑的数量,那么设边权为 $1$ ,可以正好反映拆的数量。
答案即为全图的最小割。
代码如下:
```cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int MAX = 1e5 + 7;
const int INF = 1e18;
/*dinic组件*/
struct edge
{
int next, to;
int val;
} e[MAX << 1];
int head[MAX], eid = 1;
void adde(int x, int y, int w)
{
e[++eid].next = head[x];
e[eid].to = y;
e[eid].val = w;
head[x] = eid;
}
int dep[MAX];
int flag = 0;
queue<int> q;
int S, T;
#define RUN(u) for (int i = head[u]; i; i = e[i].next)
void bfs()
{
memset(dep, 0, sizeof(dep));
dep[S] = 1;
while (!q.empty())
{
q.pop();
}
q.push(S);
while (!q.empty())
{
int u = q.front();
q.pop();
RUN(u)
{
int v = e[i].to;
if (e[i].val == 0 || dep[v])
{
continue;
}
dep[v] = dep[u] + 1;
q.push(v);
}
}
if (dep[T])
{
flag = 1;
}
}
int dfs(int u, int in)
{
if (u == T)
{
return in;
}
int out = 0;
RUN(u)
{
int v = e[i].to;
if (e[i].val == 0 || dep[v] != dep[u] + 1)
{
continue;
}
int tmp = dfs(v, min(in, e[i].val));
if (in == 0)
{
return out;
}
e[i].val -= tmp;
e[i ^ 1].val += tmp;
in -= tmp;
out += tmp;
}
if (out == 0)
{
dep[u] = 0;
}
return out;
}
int N, M;
int com[MAX];
signed main()
{
cin >> N >> M;
cin >> S >> T;
S += N;
//对于一个点 i ,我们钦定 i 为其入点,i+N 为其出点
//那么这里直接从源点的出点 (S+N) 开始。
for (int i = 1; i <= M; i++)
{
int fr, to;
cin >> fr >> to;
adde(fr + N, to, INF);
//两点之间连边,fr_out 连向 to_in
adde(to, fr + N, 0);
adde(to + N, fr, INF);//双向边
adde(fr, to + N, 0);
}
for (int i = 1; i <= N; i++)
{
adde(i, i + N, 1);//自己的出点入点连边
adde(i + N, i, 0);
}
int ans = 0;
while (1)
{
flag = 0;
bfs();
if (flag == 0)
{
break;
}
ans += dfs(S, INF);
}
cout << ans << endl;//最小割出结果
}
```
------
#### 套路一+套路四=套路四点五:网络流与LIS
有的题目,他让你求 **LIS 的条数** ,或者让你求删去哪个数会使 **LIS 的值改变** 。
这里的 LIS 实则是泛指所有转移方程为 $dp[i]=dp[j]+1$ 形式的 $dp$ 。
为什么称其为四点五是因为这一类型的题太少了,但是的的确确是一种新模型。给他一个面子。
##### 我们直接丢出例题:
[最长不下降子序列问题](https://www.luogu.com.cn/problem/P2766)
问题一:求一个序列上 LIS 的长度。
问题二:试求一个序列上 LIS 的条数。其中元素不能多次使用。
问题三:试求一个序列上 **不同的** LIS 的条数。其中 $1$ 号和 $N$ 号元素可以多次使用。
~~末 日 三 问~~
在《导弹拦截》那里 ~~打过炮~~ 的人应该会知道,LIS 有一个 $O(n\log n)$ 的优秀做法。
不会也没有关系,因为这道题只能用 $O(n^2)$ 做法。
求 LIS 的 $n^2$ 做法,状态转移方程如下:
$$dp_{\ i}=\max\{dp_{\ j}\}+1\ (num_i>num_j)$$
$dp_i$ 代表:**到 $i$ 位置时的最长上升子序列**。
我们之所以用这种 $n^2$ 方法,是因为我们要知悉每一个位置对应的 $dp$ 值。
一个 $dp$ 值为 $x$ 的位置,肯定能建出一条长为 $x$ 的路径,它是一条以 **这个位置为结束** 的 **上升子序列** 。
而这条路径上的每一条边,必然从 $dp$ 值 **低的位置** 连向 **高的位置** 。
这很好证明。如果从高的位置 $i$ 连向低的位置 $j$ ,有 $dp_i>dp_j$ :
$i$ 之前必然拖着一条长为 $dp$ 的 **上升序列** 。而 $dp$ 值低顶多只顶得住 $dp_j$ 的长度,却承受不住 $dp_i$ 。(~~破路~~)
我们便可以以此,用 $dp$ 值分层,建出一张分层图:

我们推知这条序列的 LIS=3 。
也就是说,数一数这张图上有几条长为 $3$ 的路径,其中一个点只可以使用一次。(~~唐突数数~~)
这时,我们可以 ~~转动脑髓,发动眼光~~ ,自己去构造网络流图,使得这一答案能被跑出。
因为是限制了通过 **点** 的流量,所以我们应该用套路四中的 **拆点**。把一个点拆成一个入点和一个出点,两点之间连容量为 $1$ 的边,表示限流为 $1$ 。
因为元素和元素之间没有什么限制,所以其他边容量为 $inf$ 。
而 $dp=1$ 和 $dp=LIS$ 的元素可能有多个,所以需要用到 **超级源汇** 的思想。将 $dp=1$ 的连源, $dp=LIS$ 的连汇。
最后跑最大流出答案。
而第三问,则只需要将 $1$ 号和 $N$ 号元素出入点之间的容量设为 $inf$ 即可。
实现如下:
```cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int MAX = 5e5 + 7;
const int INF = 1e18;
/*dinic组件*/
struct edge
{
int next, to;
int val;
} e[MAX << 1];
int head[MAX], eid = 1;
int cur[MAX];
void adde(int x, int y, int w)
{
e[++eid].next = head[x];
e[eid].to = y;
e[eid].val = w;
head[x] = eid;
}
int dep[MAX];
int flag = 0;
queue<int> q;
int S, T;
#define RUN(u) for (int i = head[u]; i; i = e[i].next)
void bfs()
{
memset(dep, 0, sizeof(dep));
dep[S] = 1;
while (!q.empty())
{
q.pop();
}
q.push(S);
while (!q.empty())
{
int u = q.front();
q.pop();
RUN(u)
{
int v = e[i].to;
if (e[i].val == 0 || dep[v])
{
continue;
}
dep[v] = dep[u] + 1;
q.push(v);
}
}
if (dep[T])
{
flag = 1;
}
memcpy(cur, head, sizeof(head));//这时笔者使用了弧优化
//可以去学一下
}
int dfs(int u, int in)
{
if (u == T || !in)
{
return in;
}
int out = 0;
for (int i = cur[u]; i; i = e[i].next)
{
cur[u] = i;
int v = e[i].to;
if (e[i].val == 0 || dep[v] != dep[u] + 1)
{
continue;
}
int tmp = dfs(v, min(in, e[i].val));
e[i].val -= tmp;
e[i ^ 1].val += tmp;
in -= tmp;
out += tmp;
if (in == 0)
{
return out;
}
}
if (out == 0)
{
dep[u] = 0;
}
return out;
}
int N;
int dp[MAX], num[MAX], len = 1;
//num序列上的元素值,len最长上升子序列的长度
signed main()
{
cin >> N;
for (int i = 1; i <= N; i++)
{
cin >> num[i];
}
for (int i = 1; i <= N; i++)
{
dp[i] = 1;
}
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= i - 1; j++)
{
if (num[j] <= num[i])
{
dp[i] = max(dp[i], dp[j] + 1);
//n方出答案
}
}
len = max(len, dp[i]);
}
cout << len << endl;
if (len == 1)//特判len=1
{
cout << N << endl;
//即每个元素都是一个LIS
sort(num + 1, num + 1 + N);
int tot = unique(num + 1, num + 1 + N) - num - 1;
//因为第三问要求的是不同的LIS
//故须去重后输出
cout << tot << endl;
return 0;
}
S = 0, T = N * 2 + 1;
for (int i = 1; i <= N; i++)
{
/*建各种边*/
adde(i, i + N, 1);
adde(i + N, i, 0);
if (dp[i] == 1)
{
adde(S, i, INF);
adde(i, S, 0);
}
if (dp[i] == len)
{
adde(i + N, T, INF);
adde(T, i + N, 0);
}
for (int j = i + 1; j <= N; j++)
{
if (dp[i] + 1 == dp[j] && num[j] >= num[i])
{
adde(i + N, j, 1);
adde(j, i + N, 0);
}
}
}
int ans = 0;
while (1)
{
flag = 0;
bfs();
if (flag == 0)
{
break;
}
ans += dfs(S, INF);
}
cout << ans << endl;//出第二问答案
memset(head, 0, sizeof(head));//清空
eid = 1;
S = 0, T = N * 2 + 1;
/*重新建边*/
for (int i = 1; i <= N; i++)
{
/*出入点之间*/
if (i == 1 || i == N)
{
adde(i, i + N, INF);
adde(i + N, i, 0);
}
else
{
adde(i, i + N, 1);
adde(i + N, i, 0);
}
}
for (int i = 1; i <= N; i++)
{
for (int j = i + 1; j <= N; j++)
{
/*dp值低的连向高的*/
if (dp[i] + 1 == dp[j] && num[j] >= num[i])
{
adde(i + N, j, 1);
adde(j, i + N, 0);
}
}
}
for (int i = 1; i <= N; i++)
{
/*源汇连边*/
if (dp[i] == 1)
{
if (i == 1 || i == N)
{
adde(S, i, INF);
adde(i, S, 0);
}
else
{
adde(S, i, 1);
adde(i, S, 0);
}
}
if (dp[i] == len)
{
if (i == i || i == N)
{
adde(i + N, T, INF);
adde(T, i + N, 0);
}
else
{
adde(i + N, T, 1);
adde(T, i + N, 0);
}
}
}
ans = 0;
while (1)
{
flag = 0;
bfs();
if (flag == 0)
{
break;
}
ans += dfs(S, INF);
}
cout << ans << endl;//出第三问答案
}
```
#### 套路五:最小路径覆盖问题
有的题目,它给了你一张DAG,要求你用最少的路径去覆盖它上面的每一个点。
听上去有、抽象,看来出题人也是 ~~抽象人~~ 。
我们通过画图来解释这一问题:
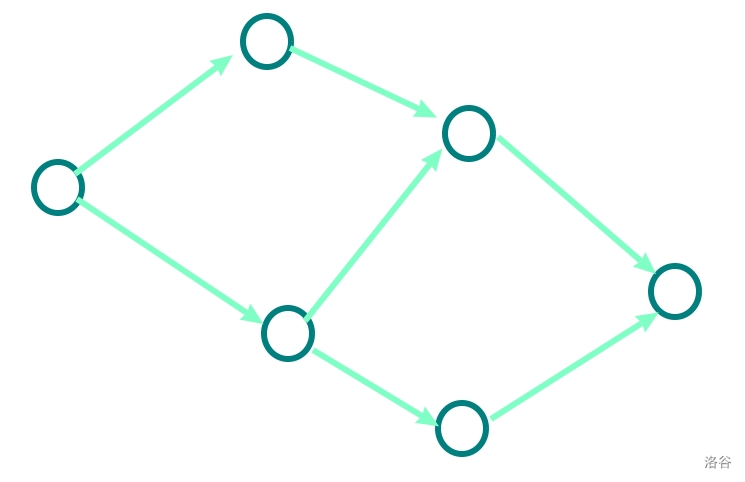
这是一张普通的 DAG 。
我们每次选择一条任意长度的路径,并将路径上的所有点染色。
如下是一种方法:

RT,粉、黄、蓝三条路径使得所有点被染色。这时我们使用的路径数量=3。
然而但凡有一点脑子的人都能看出,这条黄色路径是完全不需要的,我们用2条路径照样可以覆盖,如图:

而最小路径覆盖问题,就是解决“ **找到用最少路径覆盖全图的方案** ”这一问题的。
我们如何用网络流实现这一过程?这就要用到 **最小路径覆盖模型** 力。
先假设你是一个铁憨憨。你把每个点都用一条长度为 $1$ 的路径给覆盖了。
这时来了个 [神仙](https://www.luogu.com.cn/user/71491) ,看到你的覆盖方案,非常 $angry$ ,把你代码给删了。
她说你怎么这么蔡,很多点明明可以合并以减少路径数。
你感到非常委屈,说凭什么。
她扔出一个定理:“一张图中,如果一个点只能用在一条路径上, **路径数=点数-点之间匹配数** 。”
“这个很好证明。因为当点之间没有边时,每个点都需要一条路径去覆盖他, **路径数=点数** ;一旦有一条边(x,y)时,相当于能把这两个点合在一起,用 **一条路径** 去覆盖他们俩,所以 **路径数=点数-1** ;以此类推。”
你惊了,“那不就转化成了一道最大匹配了嘛。”
的确,但是这里依然分不出二分图来。我们需要 ~~奇技淫巧~~ 。
把一个点拆成入点和出点,永远是入点向对应的出点连边,就可以保证建出一张二分图来:
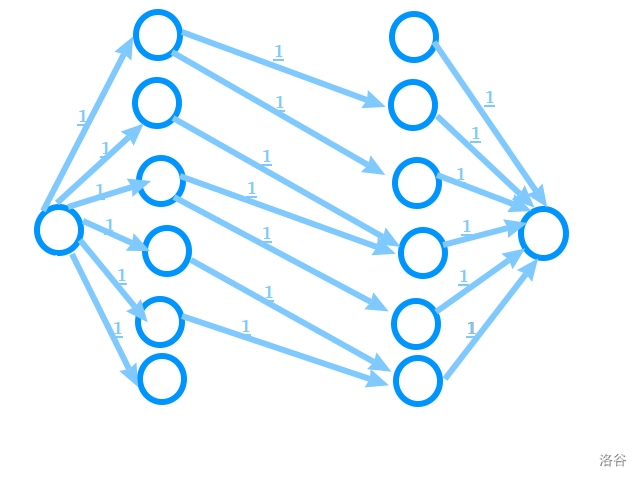
这是之前那张 DAG 建出来的图。
我们需要的是匹配数,所以图上所有入点和出点之间连的边,容量均为 $1$ ;超级源和超级汇连出的边,容量也均为 $1$ 。
这样跑最大流的答案就是 **最大匹配数的数值** 辣!
所以这就是一道最大匹配题了。
这便是最小路径覆盖的基本算法。
##### 不口嗨了,直接上例题:
这时,我们想起了之前提到的一道在讲黑白染色时提到的 ~~不讲武德的~~ 题目:
[[国家集训队]部落战争](https://www.luogu.com.cn/problem/P2172)
你以为这是一道黑白染色,只是跳的规则不固定了而已?
那还是大意了呀。
黑白染色题(如方格取数),并没有要求每个点都要被取中。而这里需要。
我们从上往下推进,因为不能回头,所以我们的推进从最顶上一行开始,到最底下一行结束。
而这个推进的过程,要 **覆盖所有的点** 。
这时,便可以用到之前的最小路径覆盖模型了。
- 先画 DAG ,点与点之间,**可达即连边**。
- 再套最小路径覆盖即可。
(实则这两步可以合成一步做)
~~希望国集好自为之,不要搞窝里斗。~~
```cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
/*dinic组件*/
const int MAX = 5e5 + 7;
const int INF = 1e18;
struct edge
{
int next, to;
int val;
} e[MAX << 1];
int head[MAX], eid = 1;
int cur[MAX];
void adde(int x, int y, int w)
{
e[++eid].next = head[x];
e[eid].to = y;
e[eid].val = w;
head[x] = eid;
}
int dep[MAX];
int flag = 0;
queue<int> q;
int S, T;
#define RUN(u) for (int i = head[u]; i; i = e[i].next)
void bfs()
{
memset(dep, 0, sizeof(dep));
dep[S] = 1;
while (!q.empty())
{
q.pop();
}
q.push(S);
while (!q.empty())
{
int u = q.front();
q.pop();
RUN(u)
{
int v = e[i].to;
if (e[i].val == 0 || dep[v])
{
continue;
}
dep[v] = dep[u] + 1;
q.push(v);
}
}
if (dep[T])
{
flag = 1;
}
memcpy(cur, head, sizeof(head));
}
int dfs(int u, int in)
{
if (u == T || !in)
{
return in;
}
int out = 0;
for (int i = cur[u]; i; i = e[i].next)
{
cur[u] = i;
int v = e[i].to;
if (e[i].val == 0 || dep[v] != dep[u] + 1)
{
continue;
}
int tmp = dfs(v, min(in, e[i].val));
e[i].val -= tmp;
e[i ^ 1].val += tmp;
in -= tmp;
out += tmp;
if (in == 0)
{
return out;
}
}
if (out == 0)
{
dep[u] = 0;
}
return out;
}
int N, M, R, C;
int idx(int x, int y)//在棋盘上获取结点编号
{
return (x - 1) * M + y;
}
int Map[57][57];
signed main()
{
cin >> N >> M >> R >> C;
S = 0, T = N * M * 2 + 1;
int tot = 0;
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
{
char c;
cin >> c;
if (c == '.')
{
tot++;//tot记录需要覆盖的点的个数
}
Map[i][j] = (c == '.' ? 1 : 0);
adde(S, idx(i, j), 1);//超级源连所有入点
adde(idx(i, j), S, 0);
adde(idx(i, j) + N * M, T, 1);//超级汇连所有出点
adde(T, idx(i, j) + N * M, 0);
}
}
int dis[5][2] = {0, 0, R, C, R, -C, C, R, C, -R};
//跳跃规则
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
{
if (Map[i][j] == 0)
{
continue;
}
for (int k = 1; k <= 4; k++)
{
int ii = i + dis[k][0], jj = j + dis[k][1];
if (ii <= 0 || ii > N || jj <= 0 || jj > M || Map[ii][jj] == 0)
{
continue;
}
adde(idx(i, j), idx(ii, jj) + N * M, INF);
adde(idx(ii, jj) + N * M, idx(i, j), 0);
//可达即连边
}
}
}
int ans = 0;
while (1)
{
flag = 0;
bfs();
if (flag == 0)
{
break;
}
ans += dfs(S, INF);
}
cout << tot - ans << endl;//最少路径数=总点数-匹配点数
}
```
#### EX-套路五:其他有趣(?)的最小路径覆盖问题泛讲:
天底下哪有裸的网络流,从来都是老阴比居多。
这一现象在“最小路径覆盖问题”上得到了充分的体现。
因为最小路径覆盖的板子局限性太高了,所以他的 **变体** 也就特别的多。
这就和 ~~“因为NEKOPARA官方给时雨的戏份太少,导致时雨的本子特别多”~~ 是一个道理。
我们挑几个范例,来剖析一下出题人的良(sang)苦(xin)用(bing)心(kuang):
- [魔术球问题](https://www.luogu.com.cn/problem/P2765)
你的正解不是搜索,ko no 网络流 da !
首先,我们制定一个总体的计划,逐个地放小球,直到放不下了为止。这时就是答案。
其次,我们想想这是怎么套上最小路径覆盖的。我们把每个球看作一个点,把两个 **相加之和为完全平方数** 的小球,所对应的点之间连边。
这也代表着我们以数 $a$ 为某柱子的顶端,我们就 **可以** 去转移到下一个与 $a$ **有连边** 的数 $b$ 。
建出一张图来就像这样:
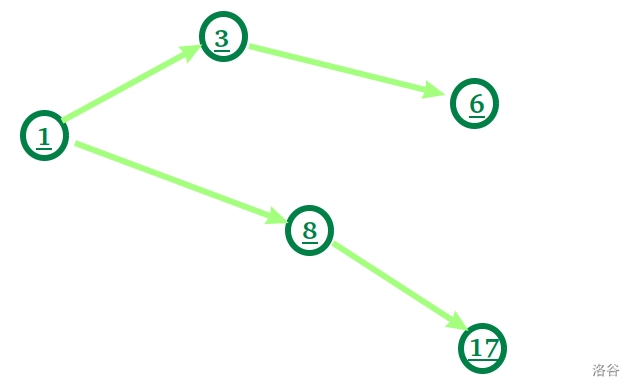
当我们把 $1$ 放在一个柱子的顶端,在他的上面,我们可以去放 $3$ ,也可以去放 $8$ 。
在图上,相当于我们在 $1$ 这个位置,可以走到 $3$ 也可以走到 $8$ 。
就这样走着走着最终会走出一条路径,这条路径上的每两个邻点之间都 **有边相接** ,意味着相加为完全平方数。
这样的一条路径正好对应了一根柱子。
那做法就很显然了,一个一个加小球,连边,当加某一个小球时,跑出的最小路径覆盖条数 **超过了柱子数** ,那这就是答案。
[~~青春猪头tyy的下半身不会梦见操场的柱子~~](https://www.luogu.com.cn/problem/U141427)
- [[JSOI2016]飞机调度](https://www.luogu.com.cn/problem/P5769)
网络瘤少有的黑题,其实还是好打的。
是什么让我们想到这是一道 **“最小路径覆盖问题”** ?
~~题解~~(闭嘴)
题目中提到“可以增开任意架飞机”,而求的是“最少使用的飞机数”,一个飞机会经过许多点……这使我们想到“最小路径覆盖”。
“最小路径覆盖”需要有 DAG ,否则就是白给。
谁设为点,是机场吗,呐?
一个机场可能多次接收航班,多次送出航班,也就是说一个机场可能会经过多次,这违背了我们DAG的初心。
那到底什么是 **一次性** 的。
在这道题里,只有航班是一次性的了,将其设为点。
谁设为边,点与点之间的转移曰边,我们这里定义:同一架飞机 **飞完一趟航班以后飞另一趟** ,这两趟航班之间就可以连边。
在什么条件下,一架飞机可以飞完一趟以后飞另一趟? 
在前一次飞完以后,能够在 **下一趟开点** 之前,赶到下一趟的 **出发站** 。我们就可以在这两趟航班之间连上边。
而这个判断里面,每一个需要的值都是可求的。
那么有人又要问了:可是题目并没有给出从一个机场赶到另一个机场所需的时间啊!
既然题目给了你这么多航班信息,你就不会用 $floyed$ **传递一下闭包** 吗。
至此此题就转化成一道最小路径覆盖问题力。
------------
#### 套路六:虚点的构建:
这并不构成一种模型,但是这类型的题挺 多 的,所以单独开出来讲。
所谓虚点者,就是这并不代表某一个元素,而是代表一种 **限制条件** 或者 **额外加成** 。
比如我们说,如果有两个物品 $a$ 和 $b$ ,每个物品有两种状态 $1$ 和 $2$ ,每个状态有不同的价值。
同时,如果我们同时选了 $a1$ 和 $b1$ ,就可以额外获得值为 $c1$ 的价值;如果我们同时选了 $a2$ 和 $b2$ ,就可以额外获得值为 $c2$ 的价值。
首先我们需要创建一个虚点,代表 $c1$ 。
这时,因为我们有 **“你可以选状态1,但你就选不了状态2了,这一切,值得吗”** 。
所以我们应该上最小割!将所有状态 $1$ 连向源,所有状态 $2$ 连向汇!
其次,如果我们选择不割 $a1$ 和 $b1$ ,就能 **保留** $c1$ 。
所以 $c1$ 与 “ $a1$ 和 $b1$ ” 不应站在割边的对立面上。而是当 **能保留a1,b1的条件满足时,一样可以保留c1** 。
~~胡乱~~ 思考得知, $c1$ 应该是从源出来而流向 $a1,b1$ 的。
那建出全图就是这样:
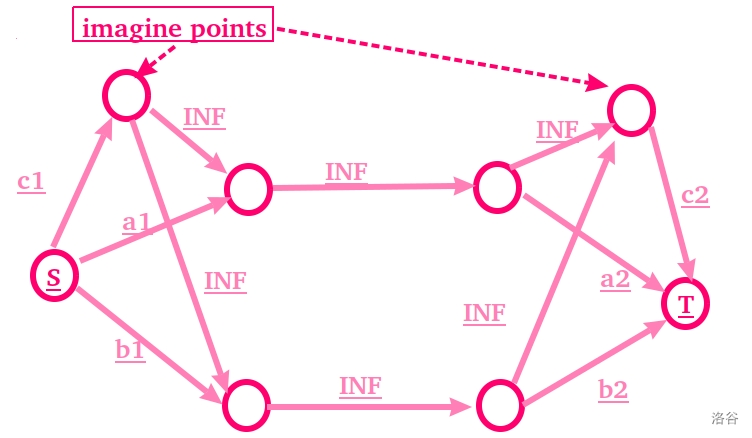
~~还挺好看。~~
手模几种情况即可验证这张图。
之后就是跑一个最小割的事。
可以看出,建立虚点的套路适用于 “~~集齐X个干员,组建幻神阵容,获得羁绊 buff~~” 的隔膜行为。
##### 下面来康例题:
[[国家集训队]happiness](https://www.luogu.com.cn/problem/P1646)
为甚么又是国集……
这道题的限制条件有亿点多,但是好在数据范围极小。
本着神仙 [shadowice1984](https://www.luogu.com.cn/user/56384) “~~大了三分,小网络流;不小不大,斜率优化~~” 的箴言。我们尝试建图跑。
对于任意两个相邻的人,他们同选某一门会有额外 $buff$ ,这说明我们要建关于 $buff$ 的虚点。
之后的事就很简单了,对于每一种 $buff$ 都建虚点,最后跑最小割即可。
图过于气 势 恢 宏,这里就不放了。
代码放一下:
```cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int LAR = 10000;
const int MAX = 5e5 + 7;
const int INF = 1e18;
/*网络流板子*/
struct edge
{
int next, to;
int val;
} e[MAX << 1];
int head[MAX], eid = 1;
int cur[MAX];
void adde(int x, int y, int w)
{
e[++eid].next = head[x];
e[eid].to = y;
e[eid].val = w;
head[x] = eid;
}
int dep[MAX];
int flag = 0;
queue<int> q;
int S, T;
#define RUN(u) for (int i = head[u]; i; i = e[i].next)
bool bfs()
{
memset(dep, 0, sizeof(dep));
dep[S] = 1;
while (!q.empty())
{
q.pop();
}
q.push(S);
while (!q.empty())
{
int u = q.front();
q.pop();
RUN(u)
{
int v = e[i].to;
if (e[i].val == 0 || dep[v])
{
continue;
}
dep[v] = dep[u] + 1;
q.push(v);
}
}
memcpy(cur, head, sizeof(head));
return dep[T] != 0;
}
int dfs(int u, int in)
{
if (u == T || !in)
{
return in;
}
int out = 0;
for (int i = cur[u]; i; i = e[i].next)
{
cur[u] = i;
int v = e[i].to;
if (dep[v] != dep[u] + 1)
{
continue;
}
int tmp = dfs(v, min(in, e[i].val));
if (!tmp)
{
continue;
}
e[i].val -= tmp;
e[i ^ 1].val += tmp;
in -= tmp;
out += tmp;
if (in == 0)
{
return out;
}
}
if (out == 0)
{
dep[u] = 0;
}
return out;
}
/*几个数组分别对应该位置选文、选理、相邻都选文、相邻都选理*/
int A[107][107];
int B[107][107];
int C[107][107];
int D[107][107];
int N, M;
int idx(int x, int y)//取标号
{
return (x - 1) * M + y;
}
signed main()
{
cin >> N >> M;
int sum = 0;
S = 0, T = 5 * N * M + 1;
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
{
cin >> A[i][j];
sum += A[i][j];
adde(S, idx(i, j), A[i][j]);
adde(idx(i, j), S, 0);//文连源
}
}
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
{
cin >> B[i][j];
sum += B[i][j];
adde(idx(i, j), T, B[i][j]);
adde(T, idx(i, j), 0);//理连汇
}
}
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
{
cin >> C[i][j];
sum += C[i][j];
int u = 2 * N * M + idx(i, j);//虚点标号
adde(S, u, C[i][j]);//价值
adde(u, S, 0);
adde(u, idx(i, j), INF);//当然他自己也要选文
adde(idx(i, j), u, 0);
/*虚点连向四个方向的点*/
if (j - 1 > 0)
{
adde(u, idx(i, j - 1), INF);
adde(idx(i, j - 1), u, 0);
}
if (j + 1 <= M)
{
adde(u, idx(i, j + 1), INF);
adde(idx(i, j + 1), u, 0);
}
if (i - 1 > 0)
{
adde(u, idx(i - 1, j), INF);
adde(idx(i - 1, j), u, 0);
}
if (i + 1 <= N)
{
adde(u, idx(i + 1, j), INF);
adde(idx(i + 1, j), u, 0);
}
}
}
for (int i = 1; i <= N; i++)
{
for (int j = 1; j <= M; j++)
{
cin >> D[i][j];
sum += D[i][j];
int u = 4 * N * M + idx(i, j);//虚点标号
adde(u, T, D[i][j]);//价值
adde(T, u, 0);
adde(idx(i, j), u, INF);//当然他自己也要选理
adde(u, idx(i, j), 0);
/*向四个方向连边*/
if (j - 1 > 0)
{
adde(idx(i, j - 1), u, INF);
adde(u, idx(i, j - 1), 0);
}
if (j + 1 <= M)
{
adde(idx(i, j + 1), u, INF);
adde(u, idx(i, j + 1), 0);
}
if (i - 1 > 0)
{
adde(idx(i - 1, j), u, INF);
adde(u, idx(i - 1, j), 0);
}
if (i + 1 <= N)
{
adde(idx(i + 1, j), u, INF);
adde(u, idx(i + 1, j), 0);
}
}
}
int ans = 0;
while (bfs())
{
ans += dfs(S, INF);
}
cout << sum - ans << endl;//总价值-最小割
}
```
--------
#### 套路七:二分与枚举:
有的题目,他条件一点都不 **给** ,或者他 **给** 得不够多。
如果我们用传统的套路,我们会寸步难行。
这时,我们如果尝试用 **枚举/二分** 的做法,相当于自己凭空创造了一个条件,这样我们就可以完成一些 ~~板子的套用~~ 模型的构造。
我们可以根据这个条件来建图跑,如果跑出的答案不满足要求,则 **调整图的形态** 再跑。
我们有时只需要改动一些边的参数,但像我这种蒟蒻只会大力重新建图。(~~这就是我常数特别大的原因之一~~)
_有关更优秀地改动边,这里埋下一个伏笔。_
您是否还记得之前的一道《魔术球问题》,那题中,我们不断放新球的过程,实际上就属于套路七中的 **枚举** 环节。
这一套路思想就这,重在运用。
##### 劲爆例题
[[POI2005]KOS-Dicing](https://www.luogu.com.cn/problem/P3425)
这题说要让“**最多的最少**”,想到了二分。
赢最多的人赢多少场,这是有边界的。
我们就可以随手二分赢最多的人的胜场。
那图呢?
我们看到,一场比赛只能有一个 **人赢** 。(雾)
所以表示比赛的点向参与的两者各连 **流量为 1** 的边。源点向所有比赛连 **流量为 1** 的边。
而我们二分到一个人最多赢 $mid$ 场。也就是一个人连向汇点最大为 $mid$ 。
跑出最大流如果 $\geq$ 比赛数,说明是 **可行的** 。尝试用更小的 $mid$ 。
最终会二分出一个答案。
输出方案就看比赛连向谁的那条边是满流即可,谁是满流谁是人赢.
```cpp
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int MAX = 5e5 + 7;
const int INF = 1e18;
/*dinic组件*/
struct edge
{
int next, to;
int val;
} e[MAX << 1];
int head[MAX], eid = 1;
int cur[MAX];
void adde(int x, int y, int w)
{
e[++eid].next = head[x];
e[eid].to = y;
e[eid].val = w;
head[x] = eid;
}
int dep[MAX];
int flag = 0;
queue<int> q;
int S, T;
#define RUN(u) for (int i = head[u]; i; i = e[i].next)
bool bfs()
{
memset(dep, 0, sizeof(dep));
dep[S] = 1;
while (!q.empty())
{
q.pop();
}
q.push(S);
while (!q.empty())
{
int u = q.front();
q.pop();
RUN(u)
{
int v = e[i].to;
if (e[i].val == 0 || dep[v])
{
continue;
}
dep[v] = dep[u] + 1;
q.push(v);
}
}
memcpy(cur, head, sizeof(head));
return dep[T] != 0;
}
int dfs(int u, int in)
{
if (u == T || !in)
{
return in;
}
int out = 0;
for (int i = cur[u]; i; i = e[i].next)
{
cur[u] = i;
int v = e[i].to;
if (dep[v] != dep[u] + 1)
{
continue;
}
int tmp = dfs(v, min(in, e[i].val));
if (!tmp)
{
continue;
}
e[i].val -= tmp;
e[i ^ 1].val += tmp;
in -= tmp;
out += tmp;
if (in == 0)
{
return out;
}
}
if (out == 0)
{
dep[u] = 0;
}
return out;
}
int N, M;
int a[MAX], b[MAX];
int akioi[MAX], tot = 0;//akioi 数组记录(表示 “这场比赛流向参赛者” 的边)的编号
/*二分函数*/
bool judge(int x)
{
memset(head, 0, sizeof(head));//暴力清空
eid = 1;
S = 0, T = 20000 + N + 1;
/*建边*/
for (int i = 1; i <= M; i++)
{
adde(S, i, 1);
adde(i, S, 0);//源连向比赛
adde(i, a[i] + 20000, 1);
akioi[i] = eid;
//记录下这条边的编号,以后输出方案要用
adde(a[i] + 20000, i, 0);
adde(i, b[i] + 20000, 1);
adde(b[i] + 20000, i, 0);//比赛连向参赛者
}
for (int i = 1; i <= N; i++)
{
adde(i + 20000, T, x);
adde(T, i + 20000, 0);//参赛者连向汇
}
int ans = 0;
while (bfs())
{
ans += dfs(S, INF);
}
if (ans >= M)
{
return 1;
}
return 0;
}
signed main()
{
cin >> N >> M;
for (int i = 1; i <= M; i++)
{
cin >> a[i] >> b[i];
}
/*二分*/
int l = M / N, r = M, ans = M;
while (l < r)
{
int mid = (l + r) >> 1;
if (judge(mid))
{
r = mid;
}
else
{
l = mid + 1;
}
}
cout << l << endl;
//以这个数为答案再跑一遍,生成方案
judge(l);
for (int i = 1; i <= M; i++)
{
if (e[6 * (i - 1) + 4].val == 0)//查询其是否满流
//(若流向一个人的边的容量变成了0,则它满流)
{
cout << 1 << endl;
}
else
{
cout << 0 << endl;
}
}
}
```
------
#### 套路INF:其他不常见技巧
- **拓扑去环**:
试想如果我们建出来的图中有环,跑网络流会得到什么结果。
可能是 $RE$ ,可能是 $TLE$ ,可能是 $WA$ ,总之跑不出正确答案。
有的题目中,环是可以被直接忽略的。这时我们就可以先跑 **拓扑排序** ,把环找出来,在之后建模时直接忽略即可。
比如下面这道题:
[[NOI2009]植物大战僵尸](https://www.luogu.com.cn/problem/P2805)
首先,这题基础建模思路就很难想到。(毒瘤题实锤)
对题目中的题意一通抽丝剥茧,我们发现,一个植物要能被吃,需要满足这两个前置条件。(看图)

- 它右边的都被吃完了(参考这里的大嘴花在坚果墙左边导致不能被吃)。
- 能攻击到这一位置的植物都被吃完了 (参考这里的坚果墙的位置被大嘴花攻击导致不能被吃
停,你刚刚说了 “**前置**” 是吧。
然后 **最大权闭合子图** 的模型不就呼之欲出了?
1. 植物 $i$ 的价值设为 $val_i$ ,正权连源,表示收益,负权连汇,表示花费。
2. 如果一个植物 $j$ 保护着 $i$ , $i$ 向 $j$ 连边 (这里包含了 **j 在 i 右侧** 和 **j 攻击到 i 的位置** 两种情况)
答案就是跑出的总的最大收益。
然后,我们会发现一个残酷的事实,如果你是僵尸,大嘴花和坚果墙你一个都吃不到。(惨)
他们互相保护,在我们建出的图上就形成了一个环。如果我们直接跑会爆炸。
这时我们就需要 **拓扑去环** 了。
在建网络流模型之前,我们需要反向建一张图,能被遍历到的结点证明它不在环上,我们用这种点再来建我们用来跑网络流的图。
之后跑最大权闭合子图即可。
- **退流**:
_伏笔消除_
如果我们要在一张跑完网络流的图上,稍作删边,再跑下一次网络流的话,我们可能要暴力重建。
但是其实这并不需要这么高的复杂度, **退流** 就是一种高效解决删边重跑的方法。
笔者突然对自己的认知产生了迷惑,先咕。
-----
那网络流部分就告一段落辣。
----
### 杜教筛
sto $\color{black}{\texttt{M}\color{red}{\texttt{iFaFaOvO}}}$ orz
杜教筛是一种高端筛法,用以快速处理积性函数的前缀和。
以前 $\color{purple}{\texttt{给}}$ 指导讲过这一高端科技,但是那时候的我连数论分块都没搞清楚,更别说杜教筛了。
昨天入的坑,今天来整理一下 $QvQ$ 。
------
#### 原理?
假设我们要来筛一个函数 $f$ 。
我们设另一个积性函数 $g$ ,然后把他们俩 **卷** 起来,得到一个 $h$ 。
也就是 $f*g=h$ 。
再设一个 $sumf$ 表示 $g$ 的前缀和。
以上是杜教筛的一些弹药。
关于 $h$ 的前缀和,展开做钬钊氪镭 **卷** 积的形式有:
$$\sum^{n}_{i}h(i)=\sum^{n}_{i}\sum_{d|n} g(d)f(\frac{n}{d})$$
$$\Leftrightarrow \sum^{n}_{i}h(i)={\color{red}{ \sum_{d}^{n}} } g(d)\sum^{\color{red}{\lfloor\frac{n}{d}\rfloor}}_{i} f(i)\quad\texttt{提出并枚举d}$$
$$\Leftrightarrow \sum^{n}_{i}h(i)={\color{red}{ \sum_{d}^{n}} } g(d){\color{royalblue}{sumf(\lfloor\frac{n}{d}\rfloor)}}\quad\texttt{将后半部分预处理}$$
$$\Leftrightarrow \sum^{n}_{i}h(i)={\color{green}{sumf(n)\cdot g(1)}}+{ \sum_{d\color{green}{=2}}^{n} } g(d){\color{royalblue}{sumf(\lfloor\frac{n}{d}\rfloor)}}\quad\texttt{提出d=1}$$
$$\Leftrightarrow {\color{green}{sumf(n)\cdot g(1)}}={ \sum^{n}_{i}h(i)-\sum_{d\color{green}{=2}}^{n} } g(d){\color{royalblue}{sumf(\lfloor\frac{n}{d}\rfloor)}}\quad\texttt{一通移项}$$
当前的这个式子启发我们,当我们易求 $h$ 的前缀和时,只需获得一个 $sumf(\lfloor\frac{n}{d}\rfloor)$ ,就能光速整除分块推知 $sumf(n)$ 。
-----
#### 数论函数的选择
~~随缘乱凑(不是)~~
回归算法本身,我们需要的 $g$ ,要求是和 $f$ **卷** 起来以后得到一个易求前缀和的 $h$ 。
所以我们需要通晓一些互 **卷** 关系:
$\mu*1=\epsilon\quad$这个很simple吧,$\mu$ 的一条性质
$\varphi*1=id\quad$ 这个看上去也很simple,$\texttt{\color{black}{R}\color{red}{ui\_R}}$神写过一篇[文章](https://www.luogu.com.cn/blog/RUI-R/ti-xie-u131347-post)证过。
$\mu*id=\varphi\quad$ 上一条柿子佐佑同 **卷** $\mu$ 即可
$f(i)=\sum_{i}^{n}(i\cdot\varphi(i)),f*id=n^2\quad$ **卷** 积拆开来发现会把$f$ 里的 $i$ 消掉得 $\sum_{d|n}n\cdot\varphi(d)$,然后套 $\varphi*1=id
-------
#### 劲爆例题
- **【模板】杜教筛(Sum)**
首当其 **冲** 的必然是模板。
题目要求 $\mu$ 和 $\varphi$ 的前缀和,我们分别来思♂尻一番。
思♂尻用什么东西来 **卷** $\mu$ ,要求和 $\mu$ **卷** 完以后要得到一个 **易于计算前缀和** 的氡氡。
通过 ~~翻博客~~ 慎重考虑后,我们选择用 $1$ 去 **卷** 它,因为 $\mu*1=\epsilon$ ,而 $\epsilon$ 的前缀和必然是 1。
所以瑇入 $g=1,h=\epsilon$ 我们有:
$${sum\mu(n)\cdot 1}={ \sum^{n}_{i}\epsilon(i)-\sum_{d=2}^{n} } sum\mu(\lfloor\frac{n}{d}\rfloor)$$
这样我们就解决了 $\mu$ 。
那 $\varphi$ 呐?
其实也很套路,因为 $\varphi*1=id$ ,而 $id$ 的前缀和,高斯哥哥已经帮我们推出公式了,是 $n\cdot(n+1)\div2$ 。
所以瑇入 $g=1,h=id$ 我们有:
$${sum\varphi(n)\cdot 1}={ \sum^{n}_{i}i-\sum_{d=2}^{n} } sum\varphi(\lfloor\frac{n}{d}\rfloor)$$
下面是瑇码,具体实现细节在注释:
```c++
#include <bits/stdc++.h>
using namespace std;
const int MAX = 6e6 + 7;
vector<int> v;//质数表(STL严重瘾君子)
int mu[MAX];
long long phi[MAX];
bool flag[MAX];
int summ[MAX];//mu前缀和
long long sump[MAX];//phi前缀和
void pre()//先线性预处理一部分的 phi 和 mu
{
mu[1] = 1;
phi[1] = 1;
for (int i = 2; i <= 6e6; i++)
{
if (!flag[i])
{
phi[i] = i - 1;
mu[i] = -1;
v.push_back(i);
}
int M = v.size();
for (int j = 0; j < M && i * v[j] <= 6e6; j++)
{
flag[i * v[j]] = 1;
if (i % v[j] == 0)
{
phi[i * v[j]] = 1LL * phi[i] * v[j];
break;
}
mu[i * v[j]] = -mu[i];
phi[i * v[j]] = 1LL * phi[i] * phi[v[j]];
}
}
for (int i = 1; i <= 6e6; i++)
{
summ[i] = summ[i - 1] + mu[i];
sump[i] = sump[i - 1] + 1LL * phi[i];//求出一部分前缀和
}
}
unordered_map<int, int> m1;
unordered_map<long long, long long> m2;//这两个map用来保存一些已经求好的前缀和(类似记忆化)
int DJSmu(int x)
{
if (x <= 6e6)
{
return summ[x];//小于6e6的预处理过了
}
if (m1[x])
{
return m1[x];//已经求过的可以记忆化
}
int ans = 1;//epsilon前缀和
for (long long i = 2/*从2开始*/, j; i >= 0 && i <= x; i = j + 1)
{
j = x / (x / i);
ans -= (j - i + 1) * DJSmu(x / i);//每次数论分块,减去mu的前缀和,而这个前缀和可以递归搞一搞
}
return m1[x] = ans;//记忆化
}
long long DJSphi(long long x)
{
if (x <= 6e6)
{
return sump[x];
}
if (m2[x])
{
return m2[x];
}
long long ans = (x) * (x + 1) / 2;//id前缀和
for (long long i = 2, j; i <= x; i = j + 1)
{
j = x / (x / i);
ans -= (j - i + 1) * DJSphi(x / i);//减去phi前缀和
}
return m2[x] = ans;
}
int main()
{
int T;
cin >> T;
pre();
int x;
while (T--)
{
cin >> x;
cout << DJSphi(x) << ' ' << DJSmu(x) << '\n';
}
}
```
_PS:小心爆精(不然就像我一样的下场)_
- **象棋与马**
~~题面要素溢出。~~
不难发现,如果一种跳跃规则是可达所有点的,那么它唯一的要求就是有能力达到 **相邻格**,如 $(0,0)$ 达到 $(0,1)$ 。
我们意识到,这一步骤其实相当于能否从 $(0,0)$ ,向各个方向~~瞎jb~~跳一跳,最后达到 $(0,1)$ 。
设我们一步能跳 $(x,y)$ ,那么 **本质不同** (唐突本质不同)的行走方案有四种:
$$(x,y) (y,x) (-x,y) (−y,x)$$
(在纵轴上走负方向其实可以看作走**负数次**正方向)
那么我们有:
$$\begin{cases}ax+by-cx-dy=0\\ay+bx+cy+dx=1\end{cases}$$
也就是说我们瞎跳过程中,有 $a$ 次 $(x,y)$ 的跳跃, $b$ 次 $(y,x)$ 的跳跃, $c,d$ 同理。
开始 $\mathbf{dark}$ 力合并两个柿子,提出 $x,y$ 来。
$$x(a+b-c+d)+y(a+b+c-d)=1$$
设 $a+b=A,c-d=B$ ,转化式子
$$x(A-B)+y(A+B)=1$$
格物致知这个柿子,我们意识到 $x,y$ 一定得 **互质** (一旦二者有非1的公约数,则结果必然 **也有** 这个公约数)。
此外,二者必须 **奇偶性互异** ,否则结果 **必然为偶** 。
因此,二者必然一奇一偶。
设此时答案是 $f(x)$ ,先记着,因为我们限定了 $x$ 的奇偶性,相当于砍掉了一半的答案,所以最后答案 $ans(x)=2\cdot f(x)$。
抓~紧~时~间~容~斥~
$$f(x)=\sum^{x}_{i}\sum^{y}_{j}[i\perp j,i j \texttt{奇偶性互异}]$$
$$=\sum^{x}_{i}\sum^{i}_{j}[i\perp j,i\texttt{为偶}\texttt{(因为两者互质所以j为偶甚至不用写)}]+{\sum^{x}_{i}\sum^{i}_{j}[i\perp j,i\texttt{为奇},j \texttt{为偶}]}$$
他欧拉反 **演** 起来了:
$$f(x)=\sum^{x}_{i}\varphi(i)[i\texttt{为偶}]+\sum^{x}_{i}\frac{\varphi(i)}{2}[i\texttt{为奇}]$$
$$ans(x)=\sum^{x}_{i}2\varphi(i)[i\texttt{为偶}]+\varphi(i)[i\texttt{为奇}]$$
因此,我们收获了一个看上去很彳亍的式子,但这还不够,$x\leq10^{11}$。
提出一个 $\varphi(i)$ 来:
$$ans(x)=\sum^{x}_{i}\varphi(i)[i\texttt{为偶}]+\varphi(i)$$
$$=\sum^{x}_{i}\varphi(i)[i\texttt{为偶}]+\sum^{x}_{i}\varphi(i)$$
$$=ans(\frac{x}{2})+\sum^{x}_{i}\varphi(i)$$
后半段可以 **杜教筛** ,前半段 **递归求解** 即可。
按 $\color{purple}{\texttt{给指导}}$ 的话说,这种“自递归函数”是未来数论出题的热点。
(这并不影响数论毒瘤爪巴)
瑇码:
```c++
#include <bits/stdc++.h>
using namespace std;
#define ull unsigned long long
#define ll long long
const int MAX = 2e7 + 7;
ll phi[MAX];
ll sum[MAX];
bool flag[MAX];
vector<ll> v;
void pre()
{
phi[1] = 1;
for (ll i = 2; i <= 2e7; i++)
{
if (flag[i] == 0)
{
phi[i] = i - 1;
v.push_back(i);
}
ll M = v.size();
for (ll j = 0; j < M && v[j] * i <= 2e7; j++)
{
flag[i * v[j]] = 1;
if (i % v[j] == 0)
{
phi[i * v[j]] = phi[i] * v[j];
break;
}
phi[i * v[j]] = phi[i] * phi[v[j]];
}
}
for (ll i = 1; i <= 2e7; i++)
{
sum[i] = (sum[i - 1] + phi[i]);
}
}
unordered_map<ll, ull> m;
ull DJS(ll x)
{
if (x <= 2e7)
{
return sum[x];
}
if (m.count(x))
{
return m[x];
}
ull ans = (__int128)(x & 1LL ? ((x + 1) / 2LL * x) : (x / 2LL * (x + 1)));
for (ll i = 2, j; i <= x; i = j + 1)
{
j = x / (x / i);
ans -= 1LL * (DJS(x / i) * (1LL * j - 1LL * i + 1LL * 1));
}
return m[x] = ans;
}
ull solve(ll x)
{
if (x <= 1)
{
return 0;
}
return solve(x / 2) + DJS(x);
}
signed main()
{
int T;
cin >> T;
pre();
while (T--)
{
ull a;
cin >> a;
cout << solve(a) << endl;
}
}
```
### 咕咕咕!