二次曲线系学习笔记
jrzhr
·
·
算法·理论
基本理论
定义(二次曲线的一般式):
f(x,y)=Ax^2+By^2+Cxy+Dx+Ey+F = 0
我们用符号 f 来简记 f(x,y)=0 这一二次曲线。
定理 1
通过平移、旋转等刚体变换,可以得到二次曲线在实平面内的所有分类:
圆,椭圆,双曲线,抛物线,两相交直线,两平行直线,单根直线,单个点。
读者自证不难(
定理 2
对平面内任意不重合的五点,必可以找到一条二次曲线通过这五点。
更进一步,若其中任意四点不共线,则该二次曲线是唯一的。
证明:
先证存在性。
设五点为 P_1, P_2, P_3, P_4, P_5,P_1P_2, P_2P_3, P_3P_4, P_4P_1 分别为 l_1, l_2, l_3, l_4。
则 l_1l_3=0 与 l_2l_4=0 过这四点。
于是有 \lambda_1l_1l_3+\lambda_2l_2l_4=0 过这四点。
把 P_5 带入,得 \lambda_1l_1l_3(P_5) + \lambda_2l_2l_4(P_5)=0
显然可以找到一组 (\lambda_1, \lambda_2) 使得该方程成立。
再证唯一性。
若有两条 f_1, f_2 过 P_1, P_2, P_3, P_4, P_5 五点,则 \forall\lambda_1, \lambda_2 \in \mathbb{R},有 \lambda_1f_1+\lambda_2f_2=0 过这五点。
不妨设 P1P2 为 x 轴,则 l_1 方程为 y=0。
在 x 轴上,取一点 Q 不与 P_i 重合,则 \exist (\lambda_1, \lambda_2) 不同时为 0,使得 \lambda_1f_1+\lambda_2f_2=0 同时过这六点。
将含 y 项与不含 y 项分离。
则 \lambda_1f_1+\lambda_2f_2 = yl+g(x),g(x) 为关于 x 的二项式。
将 P_1,P_2,P_3 三点带入,得 g(x_{P_1}) = g(x_{P_2})=g(x_Q)=0,所以 g(x) 有三零点,所以 g(x) = 0,所以 \lambda_1f_1+\lambda_2f_2 = yl 过五点。
不妨 y=0 过 P_1, P_2, P_3,l=0 过 P_4,P_5。
再取点 R 不在 yl=0 上。
则 \exist(\mu_1, \mu_2) 不同时为 0,使得 \mu_1f_1+\mu_2f_2=yl^{\rq}+h(x) 过六点。
将 P_1, P_2, P_3 带入,得 h(x) = 0,所以 \mu_1f_1+\mu_2f_2=yl^{\rq}。
但 y = 0 不过 P_4, P_5, R,即 P_4, P_5, R 在 l^{\rq} 上,但 l 过 P_4, P_5,所以 l=l^{\rq},但 R 不在 l 上,矛!
故原命题成立。
定理 3
现有任意三点不共线的四点,二次曲线 f_1 与 f_2 均经过这四点,则经过这四点的所有二次曲线形式等价于 \lambda_1f_1+\lambda_2f_2,其中 \lambda_1 与 \lambda_2 为不同时为 0 的实数。
即对三点不共线的 \{P_1, P_2, P_3, P_4\}\sube f_1\cap f_2,有 \{ 二次曲线 f\mid f(P_i)=0, \forall i = 1, 2, 3, 4\} = \{\lambda_1f_1+\lambda_2f_2\mid\lambda_1^2+\lambda_2^2\ {=}\mathllap{/\,}\ 0\}
这个集合被称为 f_1, f_2 过 P_1, P_2, P_3, P_4 四点的二次曲线系。
在 \lambda_1\lambda_2 \ {=}\mathllap{/\,}\ 0 时可以消去一个系数。
这个定理很重要,之后的每一道题都会用这个定理!
证明:
对 \forall f 过 P_1, P_2, P_3, P_4
找到一组 (\lambda_1, \lambda_2),s.t.\space \lambda_1f_1+\lambda_2f_2=f
在 f 上取一点 Q 与 P_i 不重合,则 (P_1, P_2, P_3, P_4, Q) 唯一表示 f。
对 \forall\lambda_1\lambda_2 知 \lambda_1f_1+\lambda_2f_2 过 P_1, P_2, P_3, P_4。
带入 Q,解出 \lambda_1, \lambda_2。
则 \lambda_1f_1+\lambda_2f_2 过五点。
所以 f = \lambda_1f_1+\lambda_2f_2。
二次曲线在解析几何中的应用
例题 1
已知椭圆 C_1:\dfrac{x^2}{4}+y^2=1,A_1, A_2 为左右顶点,设直线 x-my+1 与椭圆交于 P, Q 两点,A_1P 与 A_2P 交于 S,当 m 变化时,点 S 是否在恒定的直线上?说明理由。
图:
解析:
发现 C_1,A_1P, A_2Q 和 A_1A_2, PQ 构成三个二次曲线
设点 P 坐标为 (x_0, y_0),C_2=(A_1P)(A_2Q),C_3=(A_1A_2)(PQ)
C_1:x^2+4y^2-4=0
C_2:[y_0x-(x_0+2)y+2y_0][y_0x-(x_0-2)y-2y_0]=0
C_3:y(x-my-1)=0
则有 C_1, C_2 过四点二次曲线系
C_4:[y_0-(x_0+2)y+2y_0][y_0x-(x_0-2)y-2y_0]+\lambda(x^2+4y^2-4)=0
$C_4$ 的 $xy$ 项系数为 $-2x_0y_0$, $y$ 项系数为 $8y_0$。
所以 $-2x_0:8y_0=-x_0:4=1:-1=-1$,即 $x_0 = 4$。
故 $S$ 在 $x=4$ 上。
总结:找到三个二次曲线,然后求出两个的二次曲线系,对比系数即可。
#### 例题 2
已知抛物线 $C_1:y^2=4x$ 及其焦点 $F:(0, 1)$。过点 $F$ 作一直线 $l$ 与 $C_1$ 交于 $A, B$。作 $AB$ 中垂线交 $C_1$ 于 $M, N$。已知 $A, B, M, N$ 四点共圆,试求 $l$ 方程。
图: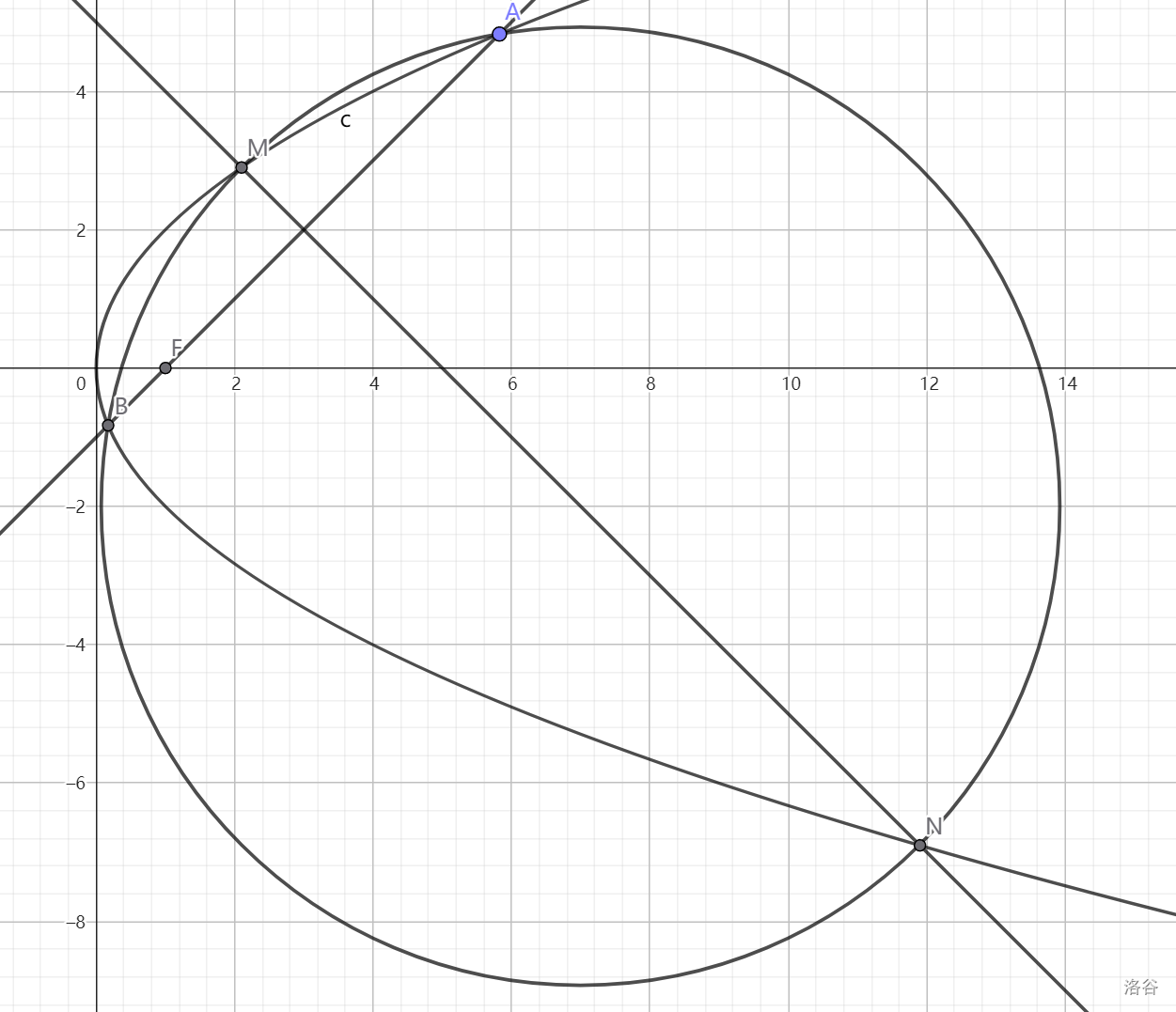
思路:首先一个知识:圆的二次曲线方程没有交叉项(就是 $xy$ 项),而且平方项系数不为 $1$。
然后我们看见三个二次曲线,就和上面一样的做法,求出来 $C_1$ 和 $(MN)(AB)$ 的曲线系,然后对比系数就好了。
过程自己写。
继续咕咕咕。