[2023] Tarjan复习
Chancylaser
·
·
个人记录
因为 Tarjan 算法涉及有向图与无向图,且在两者中应用的题型都很多样,所以这里写篇博客梳理一下。
各种 Tarjan 的实现方式终究还是在于对两个核心数组理解,两个核心数组则是 Tarjan 系列算法的精髓。
而这两个核心数组分别为为 dfn 数组和 low 数组。注意,基本的 Tarjan 算法只能求出两个核心数组而已。
有向图
主要题型为求有向图的强联通分量,以及关于它的操作。
前置芝士
有一张有向图,若对于图中任意两个节点 x,y,既存在 x 到 y 的路径 ,也存在 y 到 x 的路径,则称该有向图为“强连通图”。有向图的极大强联通子图被称为“强联通分量”。简记为 SCC。
dfn 数组
表达的含义是每个节点第一次被访问的时间顺序,该标记称之为时间戳。
由于 Tarjan 算法的所有类型 dfn 的求法一样,下面将不再赘述。
low 数组
设 subtree(x) 出发的有向边,以该点为终点。 表示搜索树中以 x 为根的子树,x 的 low 值定义为满足以下条件的节点的最小时间戳。
- 该点在栈中
- 存在一条从 subtree(x) 出发的有向边,以该点为终点。
算法流程
-
当节点 x 第一次被访问时,把 x 入栈,初始化 low[x]=dfn[x]。
-
遍历 x 的每条出边 (x,y)。
(1)若 y 没被访问过,则 (x,y) 是树边,递归访问 y,从 y 回溯后,令 low[x]=min(low[x],low[j])。
(2)若 y 被访问过,并且 y 在栈中^1,则令 low[x]=min(low[x],dfn[y])。
-
从 x 回溯之前,判断是否有 low[x]=dfn[x],若成立则不断从栈中弹出元素,直至 x 出栈,这些点构成了一个强连通分量。
**注意,题目给出的图可能并不是连通图,这时候我们需要遍历每一块求出我们想要求出的东西。以后的算法都是如此,我将不再赘述。**
### 核心代码
[板子](https://www.luogu.com.cn/problem/B3609)
```cpp
void tarjan(int p){
dfn[p]=low[p]=++cnt;
s.push(p);
vis[p]=1; ins[p]=1;
for(int i=fst[p];i;i=nxt[i]){
int j=T[i];
if(!vis[j]){
tarjan(j);
low[p]=min(low[p],low[j]);
}
else if(ins[j])
low[p]=min(low[p],dfn[j]);
}
if(low[p]==dfn[p]){
sum++;
int nw;
do{
nw=s.top(); s.pop();
ins[nw]=0;
wh[nw]=sum;
ans[sum].push_back(nw);
}while(nw!=p);
}
}
```
## SCC缩点
我们来考虑SCC的缩点。
我们可以在弹栈的过程中记录下每个节点所在的强连通分量的编号。即上面模板的 $wh[i]$ 数组。
然后对于原图中的每条边 $(x,y)$,如果发现 $wh[x]!=wh[y]$,则从 $wh[x]$ 向 $wh[y]$连边,发现最终连出来的新图是个DAG,可以做做DP啥的。
### 核心代码
[板子](https://www.luogu.com.cn/problem/P3387)
```cpp
for(int i=1;i<=n;i++){
a[wh[i]]+=val[i]; //看,这是做DP用的
for(int j=fst[i];j;j=nxt[j]){
int k=T[j];
if(wh[i]!=wh[k]){
add_edge2(wh[i],wh[k]);
deg[wh[k]]++; //跑拓扑用的出度
}
}
}
```
## 练习题
你先别急,我写完下面的无向图再说。
# 无向图
相较于有向图,题型增加了很多。
主要有:求割点,求割桥,求点联通分量及其缩点(以及点双建圆方树),求边双连通分量及其缩点。
## 前置芝士
给定一张无向连通图 $G=(V,E)$。
若对于 $x \in V$,从图中删去节点 $x$ 及其所有与 $x$ 关联的边之后,$G$ 分裂成两个或两个以上不相连的子图,则称 $x$ 为 $G$ 的**割点**。
若对于 $e \in E$,从图中删去边 $e$ 之后,$G$ 分裂成两个不相连的子图,则称 $e$ 为 $G$ 的**割边**。
-----
若一张无向连通图**不存在割点**,则称它为“点双连通图”。若一张无向连通图**不存在割边**,则称它为“边双连通图”。
**无向图的极大点双连通子图被称为“点双连通分量”,简记为“v-DCC”。**
**无向连通图的极大边双连通子图被称为“边双连通分量”,简记为“e-DCC”。**
两者统称为“双连通分量”,简记为“DCC”。
-----
还有两个定理。
### 定理一
一张无向连通图是“点双连通图”,当且仅当满足下列两个条件之一。
> 1. 图的顶点数不超过 $2$。
> 2. 图中任意两点都同时包含在至少一个简单环中。(简单环指不自交的环,也就是我们平时画出来的环。)
### 定理二
一张无向连通图是“边双连通图”,当且仅当任意一条边都包含在至少一个简单环中。
注意,这两个定理分别是判断一个无向连通图是 点双 或者是 边双 的**充要条件**。证明在算阶上有,但是我这里为了简单就不写了。
### low 数组
设 $subtree(x)$ 出发的有向边,以该点为终点。 表示搜索树中以 $x$ 为根的子树,$x$ 的 $low$ 值定义为满足以下条件的节点的最小时间戳。
1. $subtree(x)$ 中的节点。
2. 存在一条**不在搜索树**上的边,能够到达 $subtree(x)$ 的节点。
----
以下为无向图求出两个核心数组的核心代码。
注意,重边中,只有一条边是搜索树上的边,其它边也是非树边,如果 $p$ 能够通过多条边到达 $p$ 的父节点。 那么能用 $j$(也就是 $p$ 的父节点) 的 $low$ 更新 $p$ 的 $low$。
如果没有重边,按照 $low$ 的定义,如果 $j$ 是 $p$ 的父亲,因为 $p$ 到 $j$ 实际上通过搜索树上的边,与 $low$ 的定义矛盾,则不能用 $j$ 的 $low$ 更新 $p$ 的 $low$。
```cpp
void tarjan(int p,int lst){
dfn[p]=low[p]=++cnt;
for(int i=fst[p];i;i=nxt[i]){
int j=T[i];
if(!dfn[j]){
tarjan(j,i);
low[p]=min(low[p],low[j]);
}
else if(i!=other(lst)) //这里判断了不能是无向边所连的另一条边
low[p]=min(low[p],dfn[j]);
}
}
```
实际上,我们可以具体情况具体分析。有时候我们必须对于上面这种情况加以判断,有时候却可以省略不写(即不写不会对我们将要求的东西产生干扰)。详见下文中的割点和割边。
## 割边求法
无向边 $(x,y)$ 是割边,当且仅当搜索树上存在 $x$ 的一个子节点 $y$,满足
$$dfn[x]<low[y]$$
这个详细证明算阶上也有,一般想想就知道正确性了。
易得,**割边一定是搜索树中的边**,并且**一个简单环中的边一定都不是割边**。
**需要强调的是**,设 $p$ 有子节点 $j$,如果 $p$ 与 $j$ 之间有多条边,则可以用 $p$ 的时间戳更新 $j$ 的时间戳,反之则不可以。主要的原因是:如果 $p$ 和 $j$ 只有一条连边,因为如果用 $p$ 的时间戳更新了 $j$ 的 $low$,则一定会使得 $dfn[x]>=low[y]$,这样的话我们算法就不对了,所以这里每个节点的 $low$ 一定要按照无向图中的 $low$ 的正确计算方式来计算。
以下为核心代码。其中,$other(x)$ 表示 $x$ 边连双向边时候的另一条边。
```cpp
void tarjan(int p,int lst){
dfn[p]=low[p]=++cnt;
for(int i=fst[p];i;i=nxt[i]){
int j=T[i];
if(!dfn[j]){
tarjan(j,i);
low[p]=min(low[p],low[j]);
if(dfn[p]<low[j]) //判断是否 p 到 j 这条边是否是割边
bk[i]=bk[other(i)]=1; //标记这两条边(注意无向图中连的是双向边,都需要标记)
}
else if(i!=other(lst))
low[p]=min(low[p],dfn[j]);
}
}
```
## 割点求法
若 $x$ 不是搜索树的根节点,则 $x$ 是割点当且仅当**搜索树上**存在 $x$ 的一个子节点 $y$,满足
$$dfn[x] \le low[y]$$
特别地,若 $x$ 是搜索树的根节点,则 $x$ 是割点当且仅当**搜索树上**存在至少两个子节点 $y1,y2$ 满足上述条件。
以下为核心代码。
**需要注意的是**,因为我们需要的条件中带等于号,仔细想想可以发现用某个节点的父亲节点更新当前节点的 $low$ 值是可行的,故不需要判断是否重边。
```cpp
void tarjan(int p,int fp){
dfn[p]=low[p]=++cnt;
int nw=0;
for(int i=fst[p];i;i=nxt[i]){
int j=T[i];
if(!dfn[j]){
tarjan(j,p);
low[p]=min(low[p],low[j]);
if(dfn[p]<=low[j]){
nw++;
// rt为当前搜索树的根节点
if(rt!=p || nw>1) bk[p]=1;
}
}
else low[p]=min(low[p],dfn[j]);
}
}
```
## 边双
### 求法
非常简单,找到图中所有的割边,把割边都删除后,无向图会分成若干个连通块,每一个连通块就是一个“边双连通分量”。
具体实现中,一般用 $Tarjan$ 找出所有的割边,然后再对于无向图执行一次 $dfs$(不经过割边),划分出每个连通块就行了。
以下为核心代码。
```cpp
void tarjan(int p,int lst){
dfn[p]=low[p]=++cnt;
for(int i=fst[p];i;i=nxt[i]){
int j=T[i];
if(!dfn[j]){
tarjan(j,i);
low[p]=min(low[p],low[j]);
if(dfn[p]<low[j]){
bk[i]=1;
bk[other(i)]=1;
}
}
else if(i!=other(lst))
low[p]=min(low[p],dfn[j]);
}
}
void dfs(int p){
ans[sum].push_back(p); //sum为当前有多少个边双
wh[p]=sum; // 当前节点属于第sum个边双
for(int i=fst[p];i;i=nxt[i]){
int j=T[i];
if(wh[j] || bk[i]) continue;
dfs(j);
}
}
```
### 边双缩点
把每个 e-DCC 看做一个节点,把每一个割边 $(x,y)$ 看做为新图中连接 $wh[x]$ 和 $wh[y]$ 的无向边。
以下为实现方式。
```cpp
for(int i=1;i<=tot;i++){
int x=T[i],y=T[other(i)];
if(wh[x]==wh[y]) continue;
add_edge2(wh[x],wh[y]); //注意要建的是一张新图
}
```
## 点双
注意,点双连通分量和“删除割点后图中剩余的连通块”是不一样的。
若某个节点为孤立点,则它自己单独构成一个 v-DCC。除了孤立点之外,点双的大小至少为 $2$。
根据 v-DCC 定义的中的“极大”性,虽然割边不属于任何 e-DCC,但是割点可能属于多个 v-DCC。
### 求法
我们需要在 Tarjan 算法中维护一个栈,并按照如下方法维护栈中的元素。
1. 当一个节点第一次被访问时,把该节点入栈。
2. 当割点判定法则中的条件 $dfn[x]\le low[y]$ 成立时,无论 $x$ 是否为根,都要:
> (1) 从栈顶不断弹出节点,直至节点 $y$ 被弹出。
> (2) 刚才弹出的所有节点 **与节点** $x$ 一起构成一个 v-DCC。
以下为核心代码。
需要注意的是,因为我们说了:一个割点可能对应多个点双,所以我们弹栈的时候不应把 $x$ 弹掉,因为它还可能和别的点组成另一个点双。
```cpp
bool cut[N]; // 判断一个点是否为割点
void tarjan(int p){
dfn[p]=low[p]=++cnt;
s.push(p);
if(p==rt && !fst[p]){
ans[++sum].push_back(p);
return;
}
int op=0;
for(int i=fst[p];i;i=nxt[i]){
int j=T[i];
if(!dfn[j]){
tarjan(j);
low[p]=min(low[p],low[j]);
if(dfn[p]<=low[j]){
op++;
if(p!=rt || op>1) cut[p]=1;
int nw;
sum++;
do{
nw=s.top(); s.pop();
ans[sum].push_back(nw);
}while(nw!=j);
ans[sum].push_back(p);
}
}
else low[p]=min(low[p],dfn[j]);
}
}
```
### 点双缩点
比边双缩点稍麻烦。因为一个割点可能属于多个 v-DCC。
设如中共有 $p$ 个割点和 $t$ 个 v-DCC,我们建立一张包含 $p+t$ 个节点的新图,并把每个 v-DCC 和每个割点都作为新图中的节点,并在每个割点与包含它的所有 v-DCC 之间连边。容易发现,新图是一棵树。
稍微难理解些,附个图。标红的是割点。(有点抽象,但能理解就行)
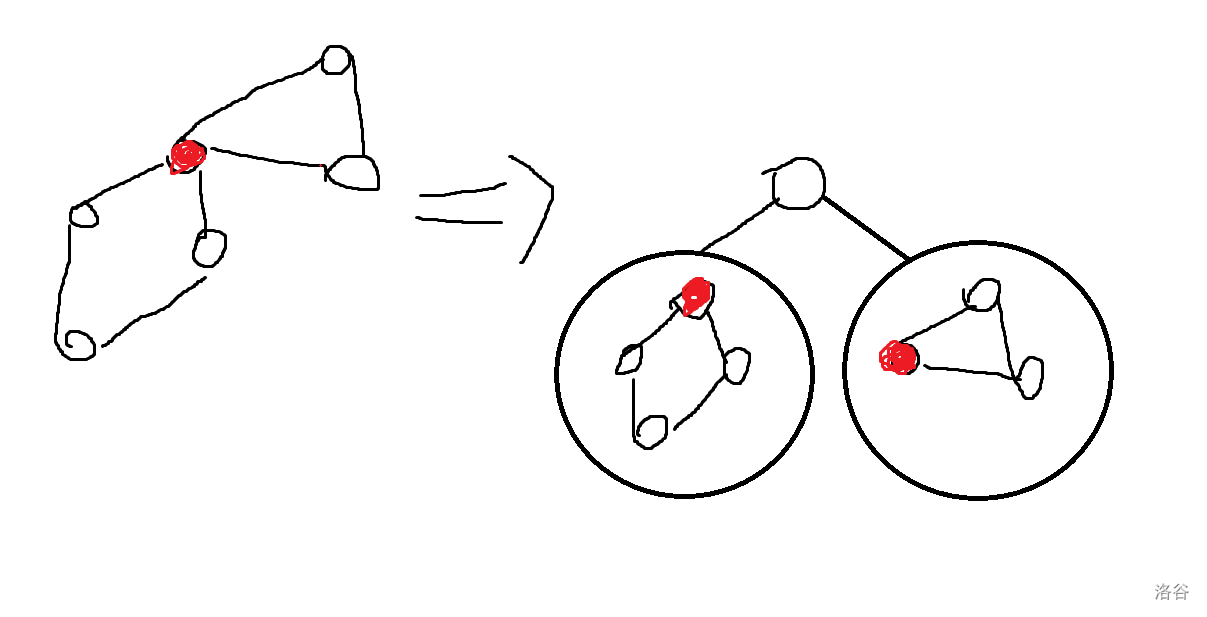
以下为核心代码。
```cpp
int num=sum; // 给每个割点赋予一个新的编号
for(int i=1;i<=n;i++)
if(cut[i])
new_id[i]=++num;
// 建立新图
for(int i=1;i<=sum;i++)
for(int j=0;j<ans[i].size();j++){
int x=ans[i][j];
if(cut[x]){
add_edge2(i,new_id[x]);
add_edge2(new_id[x],i);
}
}
```
## 点双求圆方树
我们知道,点双缩点可以求出一个点到达另一个点的必经点,可是我认为圆方树可以更直观方便地完成这一任务。
那么我们如何求出无向图上的圆方树呢?
我们求出来点双后,将点双中的每个点连向一个新的节点,这个新的节点我们称之为**方点**,而原点双的每一个点我们称之为**圆点**。至此,圆方树建成,即我们称新建出来的这个图称之为**圆方树**。
首先给出代码实现。
为了更加简洁,我将不在这份代码中标记每一个割点。
```cpp
void tarjan(int p){
dfn[p]=low[p]=++cnt;
s.push(p);
for(int i=fst[p];i;i=nxt[i]){
int j=T[i];
if(!dfn[j]){
tarjan(j);
low[p]=min(low[p],low[j]);
if(dfn[p]<=low[j]){
int nw; sum++;
do{
nw=s.top(); s.pop();
add_edge2(sum,nw);
add_edge2(nw,sum);
}while(nw!=j);
add_edge2(sum,p);
add_edge2(p,sum);
}
}
else low[p]=min(low[p],dfn[j]);
}
}
```
### 圆方树的性质
1. 圆方树显然是一棵树。共有 $n+c$ 个点,其中 $n$ 是原图点数,$c$ 是原图点双连通分量的个数。圆方树的点数小于 $2n$,这是因为割点的数量小于 $n$。
2. 圆方树中每条边连接一个圆点和一个方点。即圆点只会和方点相连,方点只会与圆点相连。
3. 我们假设新加的点的编号为 $n+1 \sim n+c$。那么对于编号小于等于 $n$ 的点构成的集合为 $S$(即原图中就存在的点),设 $x1,x2 \in S$,那么 $x1$ 到 $x2$ 的简单路径在原图中所必须经过的点即为他们在圆方树上的唯一简单路径中经过的圆点。
4. 原图删掉割点后,分成的连通块个数即此割点所连的方点个数。证明略。
性质 $3$ 的简单应用模板题:[[ABC318G] Typical Path Problem](https://www.luogu.com.cn/problem/AT_abc318_g)。
性质 $4$ 的简单应用模板题:[[ABC334G] Christmas Color Grid 2](https://www.luogu.com.cn/problem/AT_abc334_g)。
此处有个小感慨,日本的图论真的挺强的,这两个性质都是我在ABC的题目总结的。
---------
----------
----------
至此,暑假学习的Tarjan算法所涉及到的所有知识全部复习完毕。
希望之后遇到的,符合我水平范围内的 $Tarjan$ 题目都能AC。