0821考试总结
sLMxf
·
·
个人记录
题解
T1
题意
给定一张边权 0 的边,可以连接两条边 (i,j),边权 (i-j)^2。求 1\to n 的最短路。要求 \Theta(n)。
题解
显然,如果 1 和 n 在一块,那么 dis_n=0。
否则肯定要连接 \texttt{连通块1}\to \texttt{联通块x}\to \texttt{连通块n}。
记 dj_i 表示 1 到每个连通块的最短代价。DJ_i 表示 n 的。
扫一遍即可。
时间复杂度 \Theta(n)。
总结
考场上想出了正解。然后 ans 的初值应该设 1145141919810,结果写了个 114514,喜提 60。
T2
题意
给定 a_i,b_i(a_i,b_i\le 5\times 10^3),对于所有 0\sim 2m(m\le 5\times10^3) 的 k,求满足 a_i+a_j\le k\le b_i+b_j 的 k 的个数。
分析
考虑怎么暴力:枚举 i,j,将区间 [a_i+a_j,b_i+b_j] 加 1 即可,时间复杂度 \Theta(n^2)。
看到 m 比较小,考虑枚举 m。直接开一个桶。每一次枚举数值 i,j,显然这样的解有 t_i\times t_j 个。所以就这样了。时间复杂度 \Theta(m^2)。
总结
考场打了暴力。
T3
题意
每次从 1\to 任意节点,并获得路径上的“得分点”,“得分点”仅持续一回合。在每个节点都走过一次的情况下,先最小化操作次数,再最大化得分点。输出得分点。
分析
树形 DP。
首先操作次数就是叶子节点个数。考虑得分点的维护。
显然只有前 leaf 个得分点是有可能获得的。将这些节点打在树上,求个和。每个节点都会有个限制,就是这个节点的叶子节点个数。也就是:
dp_{i}=\min\left\{dp_i+\sum dp_u,\texttt{限制}_i\right\}
### 总结
考场上看错题了,寄。
## T4
### 题意
有三种字符 `A`,`B`,`C`,每次交换任意两个字符,使得所有相同的字符相邻。字符围成环。
### 分析
以下记 $Q_x$ 表示全部字母 $x$ 的数量,$P_x$ 表示区间 $P$ 的 $x$ 数量。
考虑只有两个字母的方案。显然其大致会是一个形如 `A|B|A` 的形式。枚举 $B$ 的起点,答案为 $Q_B-B_B$。
那么三个字母也同理为:`A|B|C|A`,枚举 $B$ 的起点,答案为 $Q_B+Q_C-B_B-C_C$。这样 $A$ 也会顺便排完。
考虑这样一个事情,$B$ 中 `C` 可以和 $C$ 中 `B` 直接交换。所以答案还要减去 $\min\{B_C,C_B\}$。
然后,就没有然后了。
### 总结
考场上根本不会。
## T5
### 题意
求有多少个区间**至少**有一个数**至多**出现了 $1$ 次。
### 分析
假设对于 $a_i$,上、下一个与其相等的记作 $a_l,a_r$。
那么这个区间的贡献为 $(a_i-a_l-1)(a_r-1-a_i)$。
但是这样子会有重复,~~考虑展开式子/呼叫gengen队。~~ 不过将它放到一个平面直角坐标系上面,大概会是这个样子:
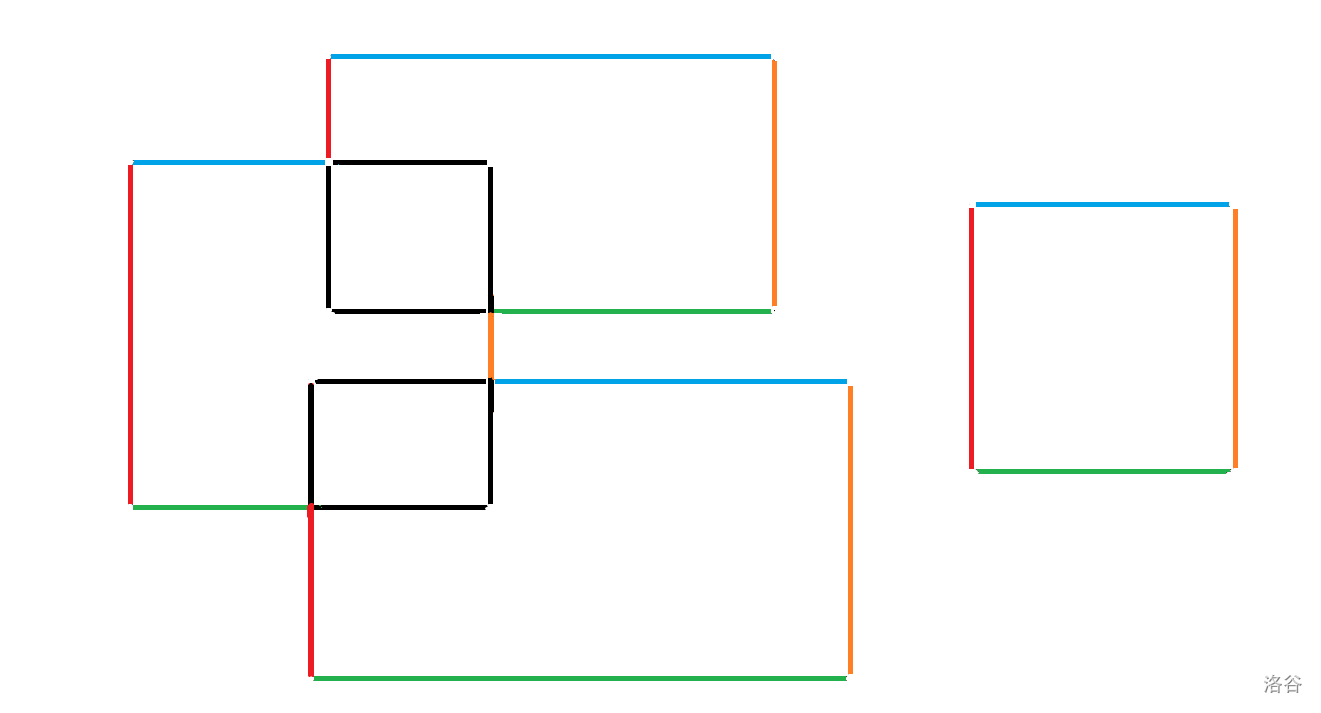
而答案就是面积。三个顶点就是 $(i,i),(i,a_l+1),(a_r-1,i)$。
扫描线模板。
### 总结
想到了扫描线,但不会打。
## T6
不会做。
# 总结
预计:100+50+0+50+0+0=200
实际:60+50+0+55+0+0=165
如果 $T3$ 想出来了,估计是 $305$,蚌埠住了。