高斯整数1
1234567_scp
·
·
个人记录
0.前置知识
-
复数的运算性质
-
初等数论的整除,同余的基本性质,\gcd 理论。
-
二次剩余的基本性质,欧拉判别式
-
费马二平方和定理
-
一点点群论知识
1. 定义
对于复数 a+bi,若 a,b\in \mathbb Q,称为高斯有理数,全体高斯有理数集为 \mathbb Q[\sqrt{-1}];
若 a, b\in \mathbb Z,称为高斯整数,全体高斯有理数集为 \mathbb Z[\sqrt{-1}]。
为区别高斯整数,称原先的整数为有理整数。
为方便叙述,下文令 Z'=\mathbb Z[\sqrt{-1}], Z=\mathbb Z, *=\times。
定义它们的四则运算为普通的复数的四则运算,即:
\begin{aligned} (a+bi)\pm(c+di) &= (a+c)\pm(b+d)i \\(a+bi)(c+di) &= (ac-bd)+(ad+bc)i\\\dfrac{a+bi}{c+di} &= \dfrac{(ac+bd)}{c^2+d^2}+\dfrac{(bc-ad)i}{c^2+d^2} \end{aligned}
显然,Z'\in Q',(Z',+,*) 是环,(Q',+,*) 是域。
称高斯整数 a+bi 的范数 N(a+bi)=a^2+b^2。
显然 N(xy)=N(x)N(y)。
称 1,-1,i,-i 为 Z' 的单位元。
称两高斯整数 a,b 相伴,若 a=be,\ e\in\{1,-1,i,-i\},这显然是一等价关系。
如:1+i,1-i,-1+i,-1-i 相伴。
2. 整除:
若对于两高斯整数 a+bi, c+di,\dfrac{a+bi}{c+di}\in Z',即 \dfrac{(ac+bd)}{c^2+d^2}+\dfrac{(bc-ad)i}{c^2+d^2}\in Z',称 c+di 整除 a+bi,这显然是一偏序关系。
这等价于 (c^2+d^2\ |\ ac+bd)\land (c^2+d^2\ |\ bc-ad)。
特别的,x\in Z,\ x|a+bi\iff x|a\land x|b。
易知若 a,b\in Z',a|b\Rightarrow N(a)|N(b)。
若对于 a\in Z',\ \ \forall b\in Z',b 不是单位元且 b 与 a 不相伴,b\nmid a,称 a 为不可约数。高斯素数显然是不可约数。
若 a\in Z',\ \ \forall b,c\in Z',\ \ a|bc\Leftrightarrow a|b\lor a|c,称 a 为高斯素数。
称有理素数集为 P,高斯素数集为 P'。
显然,若高整 a 与 b 相伴,a 是高素 \Leftrightarrow b 是高素,a 不可约 \Leftrightarrow b 不可约。
我们证明:
- 在高斯整数集上,不可约数均是素数。
- 在高斯整数集上,算术基本定理成立,即:任意高斯整数是唯一的一组素数之积(相伴算相同)。
- 高斯素数是:范数为有理素数的高斯整数,或模4余3的有理素数。
证明(初等)
证明(代数)(咕咕咕)
定义:(a,b) 为一高整满足 \forall c|a\land c|b,\ c|(a,b);
因为算基成立,断言任一两数存在 $\gcd,\mathrm{lcm}$。
设 $a=\prod\limits_{k=1}^{n}p_k^{c_k},\ b=\prod\limits_{k=1}^{n}p_k^{d_k},\ \ 0\le c_k,d_k,\ c=\prod\limits_{k=1}^{n}p_k^{\max\{{c_k, d_k}\}},\ d=\prod\limits_{k=1}^{n}p_k^{\min\{{c_k, d_k}\}}$。
显然,$c=[a,b],\ d=(a,b),\ ab=cd$。断言成立。
易知,$(Z',\gcd,\mathrm{lcm})$ 是一个格。
易知,若 $n$ 的标准分解为 $p_1^{a_1}p_2^{a_2}\cdots p_m^{a_m}$ 有约数个数 $d'(n)=4\prod\limits_{k=1}^m(a_k+1)
3. 同余
带余除法:
我们记 (a+bi)\div(x+yi)=u+vi\cdots c+di 为 a+bi 除以 x+yi 的带余除法。
我们以 (9+9i)\div(4+i) 和 (-2-4i)\div(4+i) 为例拿出其几何意义:
可见,(9+9i)\div(4+i)=2+i\cdots 2+3i,\ (-2-4i)\div(4+i)=-1-i\cdots 1+i。
我们定义 n 和 ni 围成的正方形(包括n 和 ni 这两条边,不包括另外两条边)为完系正方形,简称完形。规定余数必须在完形范围内。
再来一个图加深理解:
可知 u+vi=\left\lfloor\dfrac{ax+by}{x^2+y^2}\right\rfloor+\left\lfloor\dfrac{bx-ay}{x^2+y^2}\right\rfloor i,\ c+di=a+bi-(x+yi)(u+vi)。
我们定义:若 n|(a-b),称 a,b 同余,记为 a\equiv b(\mathrm{mod}\ n),显然这是一等价关系。
定义 n 的同余类为:\{z\in Z'\mid z\equiv z_0(\mathrm{mod}\ n)\}。
我们证明:n 的同余类有 N(n) 个,即:模 n 有 N(n) 中可能的取值。
无字证明:
将每个同余类中拿一个元素,组成的集合为完全剩余系。
我们定义 n 的一同余类与 n 互素,当该同余类与 x 同余,(n,x)=1。
从每个与 n 互素的同余类中拿一个元素,组成的集合为简化剩余系(既约剩余系,缩剩余系)。
我们说,\forall x\in Z',\ \exists y\in Z',\ N(y)\le N(n)/2,\ x\equiv y(\mathrm{mod}\ n)。
证明:
显然只需证 x\in 完形的情况。
故,完形中的数都一一同余于红色正方形中的数。
显然,红色正方形的数 y 均满足 N(y)\le N(n)/2。
故,我们可用大衍求一术(扩欧)递归有限步算出 ax+by=(a,b) 的解,即:裴蜀定理(贝祖定理)成立。(算法中 \mathrm{mod} 结果用红色正方形中的数表示)
所以:模 n 意义下,\forall x|(x,n)=1,有逆元 x^{-1}。
这表明,若 n\in P,n 的完系 Z_n' 对于加,乘法运算是一个域。
显然,孙子定理(中国剩余定理)也成立,证明与对有理整数相同,因为裴蜀定理成立。
4.剩余系
我们再证:
模 n 意义下,(f(x)\equiv f(y)\iff x\equiv y)\iff 当 x 遍历 n 的完系时,f(x) 遍历 n 的完系。
这事实上相当于说 f 是完系上的双射,结论是是显然的。
特别的,我们有:f(x)=kx+m\ ((k,n)=1),当 x 遍历 n 的完系时,f(x) 遍历 n 的完系。
这是因为 x+m\equiv y+m\iff x+y;
对于缩系,有类似结论。
我们讨论一下完系的划分。
$Z_{nm}\ (n,m\in Z')$ 可分解为
$A_k=\{a=km+x\mid x\in Z'_m\},\ k\in Z'_n$ 和
$B_k=\{b=xm+k\mid x\in Z'_n\},\ k\in Z'_m$。
---
若对于 $m\in Z'$,$\exists x^2\equiv m(\mathrm{mod}\ n)$,称 $m$ 是 $n$ 的二次剩余。
我们断言:对于 $p\in P'$,$x^2\equiv y^2\iff x\equiv\pm y(\mathrm{mod}\ p)$。
证明:$x^2\equiv y^2\iff (x+y)(x-y)\equiv 0\iff p|x+y\lor p|x-y$。
所以:
Willson 定理:$\prod\limits_{k\in Z_k'}k\equiv -1(\mathrm{mod}\ p)$。
证明: 将 $k$ 与 $k^{-1}$ 两两配对,只有 $1$ 和 $-1$ 的逆是自身,故积为 $-1$。
我们讨论 $n$ 的缩系的大小 $\varphi'(n)$,它等于 $\varphi(N(n))$。
证明:
我们证明 $\varphi'(n)$ 是一个积性函数,且当 $n$ 是素数方幂时,命题成立。
首先,当 $n$ 是素数时,成立,因为其完系中只有 $0$ 不与之互质。
其次,当 $n$ 是素数方幂 $p^m$ 时,$A=\{z=x+yp^{m-1}\mid x\in {Z^*}'_{p^{m-1}},\ y\in Z'_p\}$ 是 $p^m$ 的缩系。
因为 $p\nmid\forall z\in A\ (\because p\nmid x)$,且 $\forall z\in {Z^*}'_{p^{m}},\ z\ \mathrm{mod}\ p^{m-1}\in {Z^*}'_{p^{m-1}}$,即 $z\in A$。
显然,$|A|=N(p)|{Z^*}'_{p^{m-1}}|$,由数归,$|A|=N(p)^{m-1}(N(p)-1)=\varphi(N(p^m))$。
然后我们证明 $\varphi'(x)$ 是一个积性函数。
事实上,若 $(n,m)=1$,划分 $Z'_{nm}$ 为
$B_k=\{b=xm+k\mid x\in Z'_n\},\ k\in Z'_m$。
取出 $(n,k)=1$,即 $k\in {Z^*}'_{m}$ 的 $B_k$。
可知每一个 $B_k$ 是 $n$ 的一个完系(因为 $x$ 遍历 $Z'_n$)。
所以每一个 $B_k$ 中有 $\varphi'(n)$ 个属于 $n$ 的缩系。
$\therefore \varphi'(nm)=\varphi'(n)\varphi'(m)$。
$\therefore \varphi'(n)=\varphi'(p_1^{a_1}p_2^{a_2}\cdots)=\varphi(N(p_1^{a_1})N(p_2^{a_2}\cdots))=\varphi(N(n))$。
若 $M=\prod\limits_{k\in Z'^*_n}k$,$p\in P'\land p\ne 1+i$,$M\equiv\begin{cases}-1,& n=p^a,(1+i)p^a\\1+i,&n=2\\1 ,&otherwise\end{cases}(\mathrm{mod}\ n)
证明:
若 $n=p^a$,可知 $x\equiv x^{-1}\ (\mathrm{mod}\ n)$ 只有两解 $\pm1$,因为
原式 $\iff x^2\equiv 1\iff p^a|(x+1)(x-1)
又若 p\mid x+1,p\nmid x-1;若 p\mid x-1,p\nmid x+1。
所以将 $Z'^*_{p^a}$ 中的数与其逆元配对,只剩下 $1$ 和 $-1$,故 $M\equiv -1$。
若 $n=(1+i)p^a$,由之前的研究可得,其缩系也是 $p^a$ 的缩系。
故 $M\equiv -1\ (\mathrm{mod}\ p^a)$,即 $M\equiv -1\lor M\equiv p^a-1\ (\mathrm{mod}\ (1+i)p^a)$。
又 $2\nmid M$,故 $M\equiv -1$。
否则,设其标准分解为 $p_1^{a_1}\cdots p_m^{a_m}$,对于任一 $p_k^{a_k}$,$Z'^*_n$ 是 $Z'^*_{p_k^{a_k}}$ 的偶数倍。
故 $M\equiv 1\ (\mathrm{mod}\ p_k^{a_k})\ (k\in [1,m])$。
由孙子定理,$M\equiv 1\ (\mathrm{mod}\ n)$。
# 5.无理数的取模
我们对于整数(有理)数列 $\{x_n\}: x_n=ax_{n-1}+bx_{n-2}$ 求通项:
$$x_n=p(\dfrac{a+\sqrt{a^2+4b}}2)^n+q(\dfrac{a-\sqrt{a^2+4b}}2)^n$$
其中
$$p=\dfrac{(\sqrt{a^2+4b}-a)x_0+2x_1}{2\sqrt{a^2+4b}}$$
$$q=\dfrac{(\sqrt{a^2+4b}+a)x_0-2x_1}{2\sqrt{a^2+4b}}$$
这 $p,q$ 是无理数,这不好研究在模一个数时数列的性质。
我们希望能将无理数转化成整数,像有理数一样。
我们说:
若 $x$ 是 $p$ 的平方剩余,即 $\exists y^2\equiv x\ (\mathrm{mod}\ p)$,称 $\sqrt x\equiv y\ (\mathrm{mod}\ p)$。
由于 $p$ 是合数时比较复杂,令 $p\in P$。
对于模4余3的素数,有:若 $x$ 是 $p$ 的平方剩余,$-x$ 不是。
但是,若在 $Z[\sqrt{-1}]$ 中,$\sqrt{-x}\equiv i\sqrt x$。
故,$\forall x\in Z$,$p\mod 4=3$,$\exists\ y\in Z'$,$y^2\equiv x\ (\mathrm{mod}\ p)$。
于是,对于这样的素数(如 $1e9+7$),求递推数列的第 $n$ 项可用高斯整数做,时间,空间复杂度均比矩阵乘法快一倍。
但是,对于模4余1的素数(如 $998244353$),即使在 $Z'$ 内,也未必有平方剩余(如:$5$ 在高整中也不是 $17$ 或 $4+i$ 的平方剩余),故有时无法如此求解。
由此,我们还可证明一个关于循环节的命题:
设在模 $p$ 下数列 $\{x_n\}$ 的循环节长度为 $L$,则:
$$L\mid p^2-1$$
证明:
当 $\sqrt{a^2+4b}\in Z$ 时,模 $p$ 后,可表示为
$$x_n=pu^n+qv^n$$
由阶的知识,$pu^n$ 的循环节整除 $p-1$,$qv^n$ 也如此,故 $L\mid p-1\mid p^2-1$。
我们可以将阶的意义扩张到 $Z'$ 上。
因为 $Z'^*_p$ 事实上是一个对乘法的交换群(当 $p\not\in P$,$p\not\in P'$ 时也成立),由群论的知识,一个高整 $x$ 对 $p$ 的阶整除 $\varphi'(p)$。
当 $p\in P\land p\mod 4=3$ 时,$\varphi'(p)=p^2-1$,故 $L\mid p^2-1$。
我们同样可以将原根扩张到 $Z'$ 上,这里就从略了。
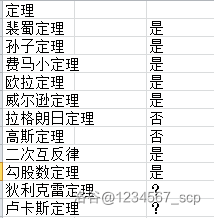
我们列出一个表格,关于那些在有理整数上的定理在高斯整数上也成立。