题解:P10256 高仿的 Migos
complexor
·
·
题解
首先,考虑没有修改时如何进行期望 dp。
以下 p_i 即为题面中 P_i,lst_i 即为题面中 x_{i+1}。
记 dp_i 为已经学习了前 i 部作品,期望还需要几分钟结束学习,那么有转移方程:
dp_i=
\begin{cases}
0&i=n\\
p_{i+1}\times dp_{i+1}+(1-p_{i+1})\times dp_{lst_i}+1&0\leq i\lt n
\end{cases}
这时,观察到这个转移式是一个一次函数的形式(此处及以下所有一次函数都有一次项不为 $0$),而一次函数的复合运算满足结合律,所以可以借此进行优化。设 $f_i(x)=\frac{1}{p_i}\times x+\frac{1}{p_i}$,则有 $b_i=f_i(b_{i-1})$。
接着,定义一次函数的“复合”运算 "$\ast$":
- 对于一次函数 $f(x)$ , $g(x)$,定义一次函数 $f\ast g$,满足 $(f\ast g)(x)=g(f(x))$。注意这里 $f,g$ 的先后顺序。
- 依照定义,容易看出在复合运算下,存在单位元 $\epsilon(x)=x$,即对于所有一次函数 $f$,有 $f\ast\epsilon =\epsilon\ast f=f$ 同时对于所有一次函数 $f$,存在逆元(记为 $f^{-1}$),满足 $f\ast f^{-1}=f^{-1}\ast f=\epsilon$,同时复合运算满足结合律(不满足交换律),所以所有一次函数关于复合运算构成一个群。
那么上面的转移可以直接从 $b_{l-1}(=0)$ 推到 $b_r$,即 $b_r=(f_{l}\ast f_{l+1}\ast\cdots\ast f_r)(b_{l-1})$(这里的 $l$ 是区间左端点加一后的 $l$,而不是输入的 $l$ )。下文中,记 $f_{[l,r]}$ 表示一次函数 $f_l\ast f_{l+1} \ast\cdots\ast f_r$,则有 $b_r=f_{[l,r]}(0)$。
定义一个记号:
- 对于一次函数 $f$ 记 $[C]f$ 为 $f$ 的常数项,显然有 $[C]f=f(0)$。
接下来,先来考察一下区间(左端点已经加一)之间的性质。可以发现若两个区间有交但不完全包含,可以处理成不交的。具体的,对于两个保护区间 $[l_1,r_1]$ 和 $[l_2,r_2]$,若 $l_1<l_2 \le r_1 < r_2$,则等效于 $[l_1,l_2-1]$ 和 $[l_2,r_2]$。
然后,加入一个大区间 $[1,n]$,并将所有区间进行处理,使得它们之间仅存在完全分离或完整包含的关系,这样这些区间构成一棵嵌套关系的树,这部分是简单的。现在,我们希望对于每一个区间 $[l,r]$,求出 $dp_{l-1}-dp_r$ 的值。这样,对于区间 $[1,n]$(即嵌套关系树的根结点所对应的区间),$dp_0-dp_n$ 即为答案。
我们再补充一些定义:
- 对于一个点 $x$,称它的“归属”为直接包含它的那个区间。更形式化的,我们称区间 $S$ 是点 $x$ 的归属,当且仅当 $x\in S$ 且不存在 $T\subsetneqq S$,使得 $x\in T$。
- 称一个“连续段”为一个区间(为了减少分类讨论,我们将左端点大于右端点的区间看作一个合法的区间,只不过它是空集),满足区间内所有点的归属相同。进一步,若一个区间内所有点的归属都是 $[L,R]$,称这个是一个关于区间 $[L,R]$ 的连续段,也称这个连续段的归属是 $[L,R]$。那么上面独立区间的转移可以推广到连续段上,具体地,对于一个关于 $[L,R]$ 的连续段 $[l,r]$,有:$\forall l\leq i\leq r$,满足 $dp_{L-1}-dp_i=f_i(dp_{L-1}-dp_{i-1})$。
- 称区间 $T$ 为区间 $S$ 的子区间(其实是直接的子区间),当且仅当 $T\subsetneq S$,且不存在另一个区间 $U$,使得 $T\subsetneq U\subsetneq S$。
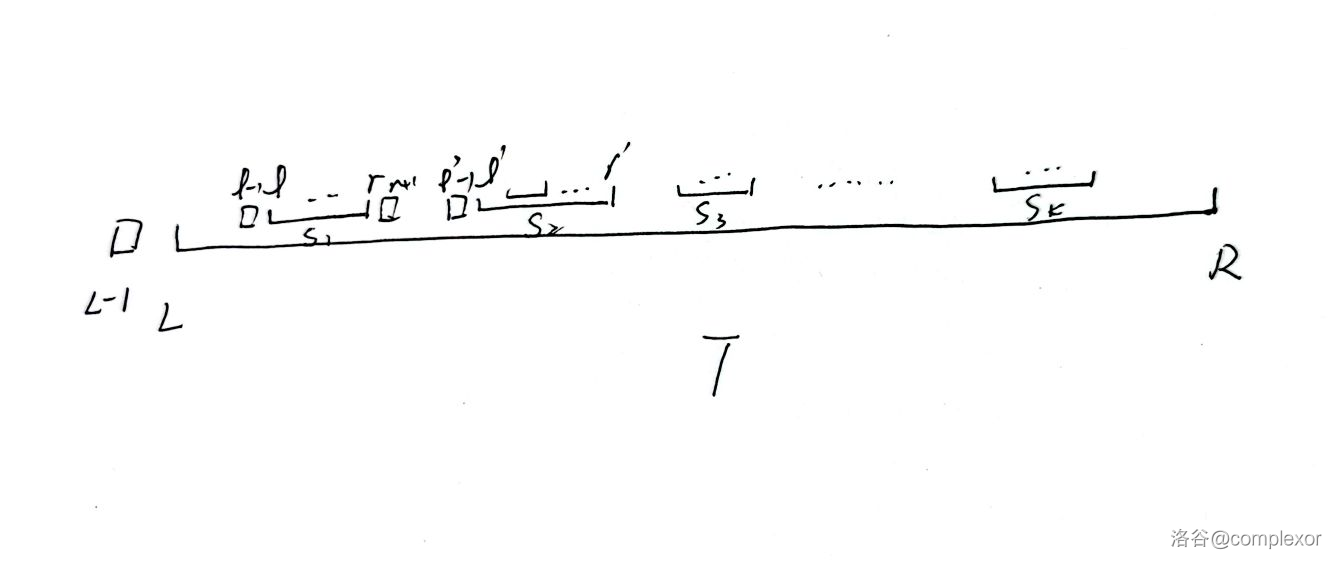
如图,假设当前所处理区间为 $T$,而我们已经递归地处理完它所嵌套的区间 $S1,S2\cdots$,现在从左往右处理那写关于 $T$ 的 **极长** 连续段(即 $T$ 相邻子区间之间的位置)。设 $S1$ 为 $[l,r]$,$S2$ 为 $[l',r']$,$T$ 为 $[L,R]$,继续前文的计算。
首先,我们已经处理好了 $dp_{L-1}-dp_{l-1}=f_{[L,l-1]}(0)$(回顾我们在一个独立区间时所进行的分析)以及 $dp_{l-1}-dp_r$(递归计算得到),并用我们前面提到的方式表示成一次函数 $dp_{L-1}-dp_{l-1}=f(0)$ 以及 $dp_{l-1}-dp_r=g(0)$。那么我们就可以得到 $dp_{L-1}-dp_r=(f+g)(0)$。
而由于 $[r+1,l'-1]$ 是关于 $[l,r]$ 的连续段,所以有 $\forall r\lt i\lt l'$,有 $(dp_{L-1}-dp_i)=f_i(dp_{L-1}-dp_{i-1})$,那么自然地,我们得到 $dp_{L-1}-dp_{l'-1}=f_{[r+1,l'-1]}(dp_{L-1}-dp_{r})=((f+g)\ast f_{[r+1,l'-1]})(0)$。这样,我们便计算完了 $S1$ 对 $[L,R]$ 内 dp 值的影响。
以此类推,依次考虑 $S2,S3,\cdots$,便可以得到 $dp_{L-1}-dp_R$。而由于区间个数为 $O(n)$,且每个点只会被一个区间直接覆盖,所以总复杂度是 $O(n)$(不包括对区间的预处理)。
如上,我们解决了不含修改的问题。而对于每个修改,仅修改了某个点 $x$ 对应的一次函数 $f_x$,并不影响整体递推和递归的结构,这提示我们将这种结构单独研究,而不考虑具体的 $f_x$。
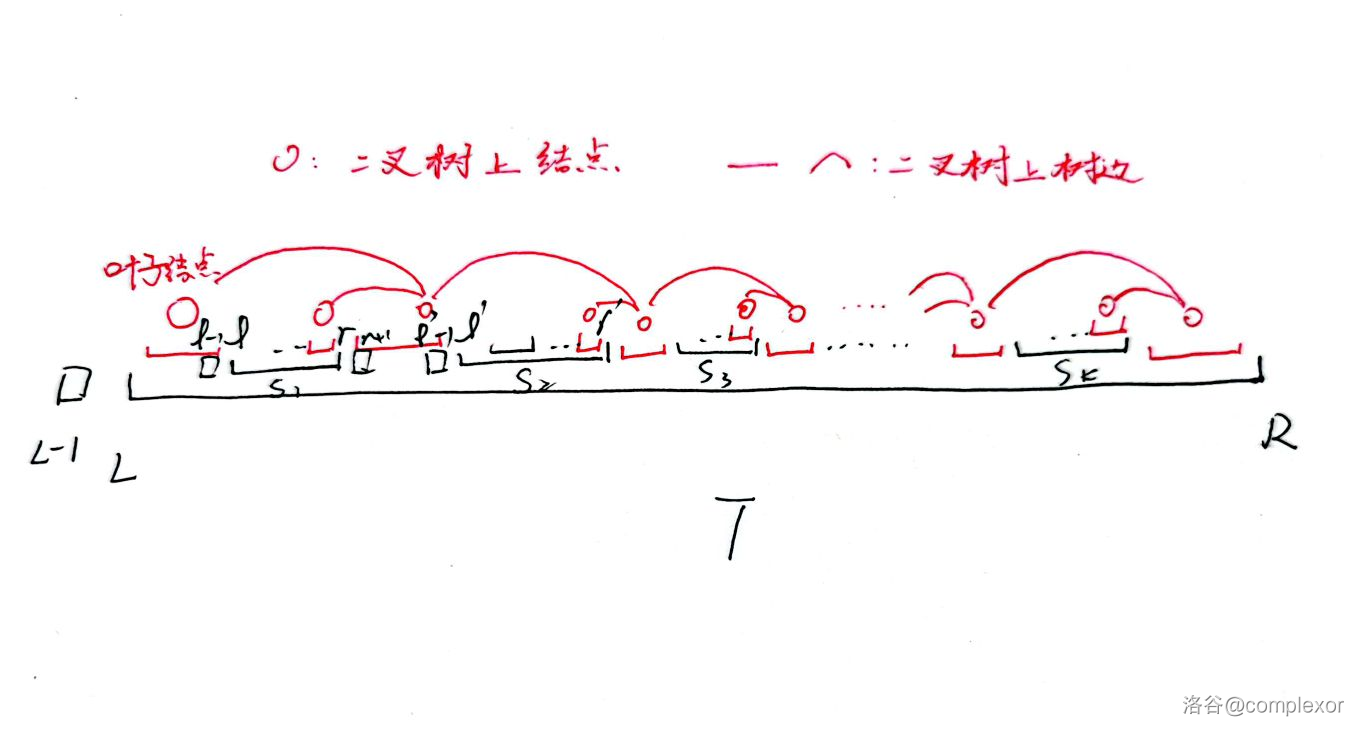
回到刚才的区间嵌套图。首先,我们发现,可以将一个 **极长** 连续段作为一个整体考虑,并将连续段内所有点的一次函数的复合作为这个连续段的一次函数(空段的一次函数可以定义为 $x$)。其次,在前面的分析中,对于 $l'-1$ 的计算用到了 $l-1$ 与 $r$,所以对 $[L,l-1],[pos,r],[r+1,l'-1]$ ($pos$ 是 $r$ 所在连续段的左端点)这几个位置建点,并连边 $([r+1,l'-1],[L,l-1])$,$([r+1,l'-1],[pos,r])$。
一般化地,将所有极长连续段(总共应该有 $2m-1$个,$m$ 为处理后的区间个数)建成一个点,对于每个关于 $T$ 的极长连续段 $S$,如果 $S,T$ 的左端点重合,那么 $S$ 所对应的点为叶子。否则,可以找到 $S$ 左侧的所有关于 $T$ 的极长连续段中最靠右的一个 $S'$,以及 $S$ 左侧所有 $T$ 的子区间中最靠右的一个 $T'$(简单的说,就是上一个关于 $T$ 的极长连续段和是一个 $T$ 的子区间),并建边 $(S,S')$,$(S,T')$。这样,会得到一颗结点数为 $2m-1$ 的二叉树,且每个非叶结点恰有两个子结点。上图为建树方法示意。
现在,可以脱离原来的区间嵌套结构,将所有转移放在新建的树上。对于树上的一个结点 $u$,它对应的连续段为 $[l,r]$,其归属为 $[L,R]$,那么设一次函数 $g_u(x)$,满足 $dp_{L-1}-dp_r=g_u(0)$,将上面得到的转移方式改写成($Lf$ 表示树上的叶子结点的集合):
$$
g_u=
\begin{cases}
f_{[l,r]}&u\in Lf\\
(g_{lchild(u)}+g_{rchild(u)})\ast f_{[l,r]}&O.W
\end{cases}
$$
而所求即为 $g_{root}(0)=[C]g_{root}$。
这个形式还是不够利于维护,所以进一步发掘性质。考虑三个一次函数 $a,b,c$,不难发现一个类似分配律的性质: $(a+b)\ast c=a\ast c+b\ast c-[C]c$。如果我们只考虑常数项为零的一次函数,那么此时的一次函数复合相当于一次项相乘。记 $h_u$ 为树上“前缀”复合,定义为:
$$
h_u=
\begin{cases}
f_{[l,r]}&u=root\\
f_{[l,r]}\ast h_{father(u)}&O.W
\end{cases}
$$
如果所有的 $f$ 常数项都为零,则 $g_{root}=\sum_{u\in Lf}h_u$(证明不难)。不幸的是,现在我们的一次函数有了常数项。好在事实上,$[C]g_{root}$ 仍然有优秀的性质,它满足:$[C]g_{root}=[C](\sum_{u\in Lf}h_u-\sum_{u\notin Lf}h_u)$。[证明在这里。](https://www.luogu.com.cn/paste/tpdp6uns)
现在,做法就很明了了:在二叉树的 $dfs$ 序列上建立线段树,对于原树的叶子结点维护 $h_u$,对于原树上的非叶子结点维护 $-h_u$,并用线段树维护区间和。
那么,每个修改相当于修改一个结点的 $f_{[l,r]}$(这一部分可以另用一棵线段树维护)。设修改前的一次函数为 $s$,修改后为 $s'$,修改的结点为 $u$,对于 $u$ 子树中每个 $v$,将 $h_v$ 修改为 $h_v\ast (s\ast h_{father(u)})^{-1}\ast(s'\ast h_{father(u)})$。利用结合律,我们记 $f=(s\ast h_{father(u)})^{-1}\ast(s'\ast h_{father(u)})$。
当对线段树某个点代表的 $[L,R]$ 这一 $dfs$ 序区间内所有 $h$ 复合上 $f=ax+b$ 时,考虑它对区间函数和的影响。设区间 $[l,r]$ 内有 $c_+$ 个代表叶子结点,$c_-$ 个代表非叶子结点,则只需要将区间函数和 $\times k$(此处乘法是一次项、常数项同时乘 $k$,而不是复合),并将区间函数和的一次函数的常数项加上 $b(c_+-c_-)$,同时打上懒标记即可。
而修改中用到的 $h_{father(u)}$ 正好是线段树所维护的,单点查询即可(注意正负)。
而询问答案即为线段树根节点的值。
处理区间时间复杂度为 $O(m\log n)$,总时间复杂度为 $O((m+q)\log n)$,空间复杂度 $O(n)$。