题解:P7697 [COCI2009-2010#4] OGRADA
wzxwowu
·
·
题解
思路
第一个问题
根据题目 样例1
$a[1]=5~,~a[2]=3~,~a[3]=4~,~a[4]=4~,~a[5]=5
我们需要满足题目刷的限制,保证刷子完全接触栅栏,也就是每次刷的时候不能刷到空的;
那么对于 i 到 i+k-1 刷的高度就是 \min(a[j])~,~1 \leq j \& \& j \leq i+k-1 ;
我们设一个 k 数组把这个高度记下;
我们做一遍单调队列就可以求出$\min(a[j])~,~1 \leq j \& \& j \leq i+k-1$ ,也就是 $h[i]$ ;
求出后 $h[1]=3$ , $h[2]=3$ , $h[3]=4$ ;
很明显每条木板都有一个,能刷的最大高度;
如样例:
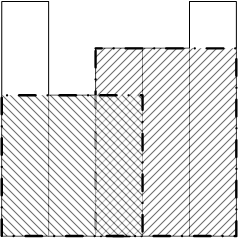
$mx[1]=3~,~mx[2]=3~,~mx[3]=4~,~mx[4]=4~,~mx[5]=4$ ;
我们会发现 $mx[3]$ 可以刷到的$h[i]$ 有两个 $3$ 和 $4$ ;
但是我们要取 $3$ 的 $\max(h[i])$ ,也就是取 $4$;
所以$mx[i]=\max(h[j])~,~i-k+1 \leq j \& \& j \leq i$ ;
再做一遍单调队列求出每个 $mx[i]$ 就ok了;
这样刷不到的地方就是 $\sum ^n _i a[i]-mx[i] $ ;
这样我们就很轻松地解决了第一问;
## 那么第二问怎么求呢?
首先在$i+k-1$ 这个范围内,如果 $mx[i] \neq mx[j]$ 那么 ,$ans++$ ;
刷的最大高度不同,则说明在这个范围内刷了多次;
如样例
在$a[1]$ 到 $a[3]$ 之间 $mx[1] \neq mx[3]$ ,则这个范围内刷了$2$ 次;
如果刷的区域超出了上次刷的宽度,那么说明又刷了一次;
什么意思呢?
我们来看下面这个特殊的样例
$n=5~,~k=3$ ,$a[i]=3~,~1 \leq i \& \& i \leq n $;
这个样例中没有出现不同的$mx[i]$,但是很明显也刷了两次;
第一次从$1$ 刷到了 $3$ ,需要刷的区域 $4$ 超出的这个范围,说明再刷了一次;
所以如果刷的区域超出了上次刷的宽度,那么说明又刷了一次;
所以我们可以设一个 $pre$ 表示上次的$mx[i]$ ,设 $pra$ 表示上次刷的宽度,也表示刷到了 $i$;
那么
```
if(mx[i]!=pre) //如果刷的高度不同,说明从 i 又刷了一次
{
ans++;//答案加1
pra=i+k-1;//记录下刷到的边界
}
if(i>pra)//如果超出了这个边界,说明后来 i 刷了一次
{
ans++;//统计答案
pra=i+k-1;//更新边界
}
```
这样统计$ans$ 就ok了;
同样就轻松地解决了第二个问题;
那么没有第三个问题了,就直接上代码吧;
# 渣渣代码
```cpp
#include<bits/stdc++.h>
#define re register
typedef long long ll;//被坑过一次了,习惯每次都开long long 了
using namespace std;
inline ll read()
{
ll a=0,f=1; char c=getchar();
while (c<'0'||c>'9') {if (c=='-') f=-1; c=getchar();}
while (c>='0'&&c<='9') {a=a*10+c-'0'; c=getchar();}
return a*f;
}//快读比 scanf 好打多了
ll n,k;
ll a[1000010],h[1000010],mx[1000010];
ll q[1000010];
int main()
{
n=read(); k=read();
for(re ll i=1;i<=n;i++)
a[i]=read();
ll head=1,tail=0;//单调队列初始头尾
for(re ll i=1;i<=n;i++)
{
while(head<=tail&&i-q[head]+1>k)//如果长度超过刷子宽度 k
head++;// 那就踢队头
while(head<=tail&&a[q[tail]]>a[i])//找一个最小值,因为不能刷到空白,所以刷的高度就不能高于木板最小值
tail--;// 踢队尾
q[++tail]=i;//入队
if(i-k+1>=0)//下标不为0
h[i-k+1]=a[q[head]];//记录
}
head=1,tail=0;//重置
for(re ll i=1;i<=n;i++)
{
while(head<=tail&&i-q[head]+1>k)//限制范围
head++;// 又踢队头
while(head<=tail&&h[q[tail]]<h[i])//找一个h[i]的最大值
tail--;// 踢掉,踢掉!!!
q[++tail]=i;//入队
mx[i]=h[q[head]];//再来记录
}
ll sum=0;
for(re ll i=1;i<=n;i++)//For
sum+=a[i]-mx[i];
printf("%lld\n",sum);//输出第一个问题的答案
ll ans=0;
ll pre=0,pra=1<<30;//不需要设为1<<30,只是博主之前用另一种方法写的时候忘改了
for(re ll i=1;i<=n;i++)
{
if(mx[i]!=pre) //如果刷的高度不同,说明从 i 又刷了一次
{
ans++;//答案加1
pra=i+k-1;//记录下刷到的边界
}
if(i>pra)//如果超出了这个边界,说明后来 i 刷了一次
{
ans++;//统计答案
pra=i+k-1;//更新边界
}
pre=mx[i];
}
printf("%lld\n",ans);//输出
//return 0;
}
```
------------