一些快速笔记
w9095
·
2024-09-18 15:47:17
·
算法·理论
前言
这是一些我没时间整理成专栏笔记知识点的快速笔记。
代码合集
斜率优化
WQS 二分
线段树维护区间历史最值
对序列序列 A ,区间加,区间和,区间最值,区间历史最值。
O(m\log n)
前三个操作是平凡的。我们维护历史最值数组 B ,考虑加法标记的影响。假设对一个区间不停地进行区间加,则这个区间的加法标记值 tag 会一直改变。只有当 tag 达到最大时,下传的时候才可以使儿子达到当前最大,且只有当前最大才有可能更新历史最大。 于是我们维护一个 tag_{mx} 记录没有下传的最大的懒标记,每次访问时下传即可。
注意先更新 $mb$ 再更新 $ma$,先更新 $tag2$ 再更新 $tag1$。
### 吉司机线段树
***
([【模板】线段树 3(区间最值操作、区间历史最值)](https://www.luogu.com.cn/problem/P6242))对序列序列 $A$,区间加,区间和,区间最值,区间取 $\min$。
$O(m\log^2 n)
对于每个节点维护 mx 表示节点内最大值,cnt 表示节点内最大值的数量,se 表示节点内次大值。对于每一个节点,更新对 k 取 \min 时一直递归下去,直到 se\lt k\lt mx ,直接更新最大值即可。需要一个最大值加法标记 tag1 和一个所有值加法标记 tag2 。下推的话找子节点的中包含最大值的下传 tag1 为最大值最大值加法标记,否则下传 tag2 为最大值加法标记。
势能分析时间复杂度为 O(m\log^2 n) ,显然我不会证。
离线操作树
支持离线的带回退历史版本数据结构问题。
我们把操作离线 下来,建成一棵树。将操作顺序编号 ,对于编号为 i 的普通的修改 ,查询 操作,连到操作 i-1 的后面作为子节点。对于回退 到操作 x 之后操作,连到操作 x 的后面作为子节点 。我们从 0 开始 DFS 遍历 这一整棵树,处理修改,回答询问,回溯 的时候撤销 修改操作的影响,再去递归另一个子节点。于是我们就解决了支持离线的带回退历史版本数据结构问题。
同余最短路
似乎没有固定的模板?
其实是一类特殊的建模方式。这一类问题通常可以按照对某一个数 x 取余的剩余系 考虑,即把除以 x 余数相同的数 看作一个点 。此时我们如果发现同一个剩余系 中只需要其中最小 的数就可以了,我们就可以在这些剩余系中连边,从一个剩余系开始跑最短路 ,就可以求出同一个剩余系中最小的数。之后使用这个信息接着做后面的步骤。
子集反演
学习资料1 学习资料2
恰好是某个子集和在这个子集中钦定/钦定这个子集之间的转换。
子集枚举似乎就是 O(2^n) 的。
设 S,A 表示两个集合。函数中自变量为满足某种条件的元素集合 A 。
$2$:设 $f(S)$ 表示 $A=S$ 时的答案,$g(S)$ 表示 $A\subseteq S$ 时的答案,则有 $g(S)=\sum_{S\subseteq T}f(T)$,子集反演得 $f(S)=\sum_{S\subseteq T}(-1)^{\mid T\mid-\mid S\mid}g(T)$。
搞反演的第一步是**设计两个状态**,且需满足其中一个可以**方便求得**、另一个可以方便**得出答案**、两者之间存在**关系式**。之后代式子就行了吧。另外反演技巧也不是只能单独使用,比如子集反演就可以用在状压 DP 上踹飞集合维度。
### 最小表示法
***
([【模板】最小表示法](https://www.luogu.com.cn/problem/P1368))给定一个字符串,求与这个字符串循环同构的字符串中字典序最小的那个。
***
循环类问题,我们考虑把字符串**复制**一遍接在**末尾**,显然 $s[i,i+n-1](1\le i\le n)$ 是一个与原字符串**循环同构**的字符串,记作 $t[i](1\le i\le n)$。考虑到如果对于 $(i,j)$ 存在**最小**的 $k$ 使得 $s[i+k]\gt s[j+k]$,则所有 $t[i]$ 到 $t[i+k]$ 均**不可能**成为最小表示,考虑**直接跳过**。$s[i+k]\lt s[j+k]$ 同理。
于是,我们记录**双指针** $i=1,j=2$ 来记录位置。每次我们考虑从 $0$ 开始枚举 $k$,找到最小的 $k$ 使得 $s[i+k]\neq s[j+k]$。之后按照 $s[i+k]$ 和 $s[j+k]$ 的**大小关系**选择把 $i$ 或 $j$ 往后跳 $k+1$ 个即可。显然 $i,j$ 都**至多**跳 $n$ 次,总时间复杂度 $O(n)$。
有一个细节,如果 $i=j$,就直接让其中**某一个**自增。
### 反射容斥
[学习资料](https://www.cnblogs.com/Hanghang007/p/18159154)
***
例题 $1$:方格路径计数问题,只能向上或向右走,求从 $(0,0)$ 走到 $(n,n)$ 的方案数。
***
考虑向上和向右走的顺序**不影响**,即在 $2n$ 个位置中**选择** $n$ 个出来填向上,答案为 $C_{2n}^n$。
***
例题 $2$:方格路径计数问题,只能向上或向右走,不能经过 $y=x+1$,求从 $(0,0)$ 走到 $(n,n)$ 的方案数。
***
直接求显然不好算,考虑用**总数减去不合法**的路径数量。这是**反射容斥**的经典技巧,我们考虑把碰到 $y=x+1$ 这条线的前面一部分以这条线为**对称轴翻折**。
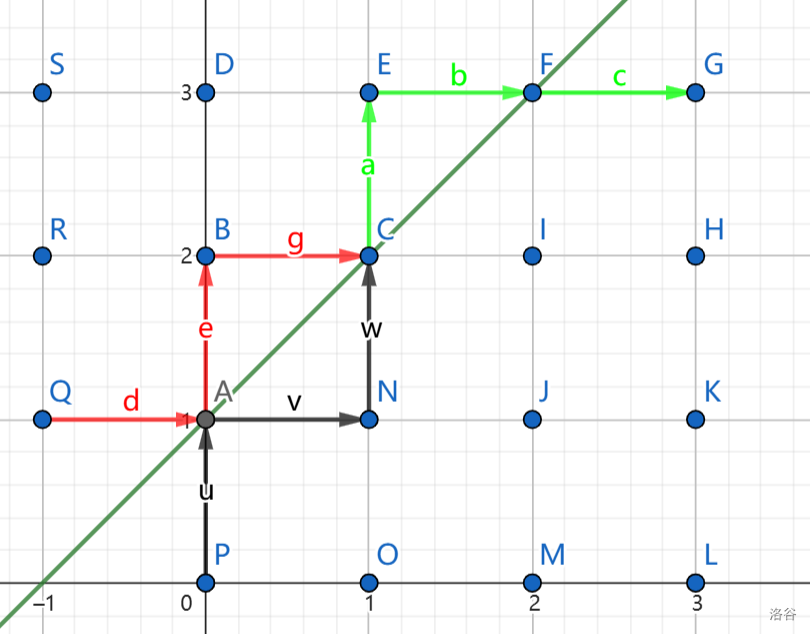
我们发现不合法的路径**等价于**从 $(-1,1)$ 到 $(n,n)$ 的方案数。因为显然不合法路径和从 $(-1,1)$ 到 $(n,n)$ 的路径**一一对应**,形成**双射**,即 $C_{2n}^{n+1}$。最终的答案为 $C_{2n}^n-C_{2n}^{n+1}$,即 $\text{Catlan}(n)$。
***
例题 $3$:([[SCOI2010] 生成字符串](https://www.luogu.com.cn/problem/P1641))方格路径计数问题,只能向上或向右走,不能经过 $y=x+1$,求从 $(0,0)$ 走到 $(n,m)$ 的方案数。
***
比较平凡,总路径就是 $C_{n+m}^n$,不合法的路径翻折之后其实就是从 $(-1,1)$ 到 $(n,m)$ 的路径,最终的答案为 $C_{n+m}^n-C_{n+m}^{n+1}$。
***
例题 $4$:方格路径计数问题,只能向上或向右走,不能经过 $y=x+a$,求从 $(0,0)$ 走到 $(n,m)$ 的方案数。
***
同样比较平凡,对称点改变成了 $(-a,a)$,答案为 $C_{n+m}^n-C_{n+m}^{n+a}$。
***
例题 $5$:([[JLOI2015] 骗我呢](https://www.luogu.com.cn/problem/P3266) 转化后)方格路径计数问题,只能向上或向右走,不能经过 $L:y=x+l$ 和 $R:y=x+r(l\lt 0\lt r)$,求从 $(0,0)$ 走到 $(n,m)$ 的方案数。
***
考虑可能会**多次接触**两条直线,我们考虑记仅包含 $L$ 和 $R$ 的字符串表示依次接触的直线,多次连续重复接触仅记一次。多次接触两条直线,我们也对**最后一次**接触前的部分**多次轴对称**。对于一个字符串 $s$,假设最后的起点是 $(x,y)$,则答案 $f(s)=C_{n+m}^n-C_{n-x+m-y}^{n-x}$。
考虑**容斥**,枚举每个字符串,使用**容斥原理**进行计算。
$$\text{ans}=f(\varnothing)-f(L)-f(R)+f(LR)+f(RL)-f(LRL)-f(RLR)\dots$$
进行化简,得到最终的式子。注意到此时 $k$ 只有 $\frac{n}{r-l}$ 中取值,直接计算即可。
$$\text{ans}=\sum_{k\in\mathbb{Z}}C_{n-k(r-l)}^{n+m}-C_{n-k(r-l)+r}^{n+m}$$
如果忘记了这个公式也没关系,推一下对称公式后枚举交错序列是先 $L$ 还是先 $R$ 暴力计算即可。边界的话就是 $x\gt n$ 或 $y\gt m$ 的时候。
对称公式:点 $(x,y)$ 关于 $y=x+a$ 对称后位于 $(y-a,x+a)$。
### Prufer 序列
***
例题 $1$:([【模板】Prufer 序列](https://www.luogu.com.cn/problem/P6086))在 $O(n)$ 时间内把一棵树的 Prufer 序列和父亲序列互相转化。
***
Prufer 序列的定义:每次选择一个**编号最小**的**叶结点**并删掉它,然后在序列中记录下它**连接到**的那个结点。重复 $n-2$ 次后就只剩下**两个结点**,算法结束。
这个构造过程可以 $O(n)$ 维护。具体的,使用一个指针 $p$ 从 $1$ 扫到 $n$,如果遇到叶子节点就**直接删除**。注意到删除一个叶子节点后**至多**新增一个叶子节点,所以如果新增叶子节点,我们比较这个叶子节点编号和 $p$ 的大小,如果**小于**,**直接删除**并重复这个过程,将新的叶子节点和 $p$ 比较。否则**不管它**,继续往后扫。正确性显然。这就是父亲序列转 Prufer 序列的过程。
这个过程生成的 Prufer 序列有如下性质:
$1$:这是一个把**带标号的无根树**用一个**唯一**的整数序列表示的方法。更一般的,带标号的无根树和 Prufer 序列构成**双射**。
$2$:Prufer 序列构造结束后一定剩下两个点,其中一个是 $n$。
$3$:一个节点在 Prufer 序列中的**出现次数**为其**度数减 $1$**,**叶子节点不在** Prufer 序列中出现。
根据 Prufer 序列的性质,我们可以使用 Prufer 序列重构树,求出父亲序列。
具体的,我们可以根据 Prufer 序列得到树上每个点的**度数**。我们也可以得到**编号最小**的叶结点,而这个结点一定与 Prufer 序列的**第一个数**连接。于是我们同时**删掉**这两个结点和它们连接节点的度数。
于是我们每次找到一个度数为 $1$ 的**编号最小**的节点,然后**删除**这个节点的出度并记录父节点。重复直到只剩两个节点。为了还原最后一部分,我们在原 Prufer 序列后添加一个 $n$,这样就可以处理最后两个节点的关系。同样可以用类似的方法 $O(n)$ 还原树。
***
例题 $2$:(Cayley 公式,[UVA10843 Anne's game](https://www.luogu.com.cn/problem/UVA10843))求大小为 $n$ 的完全图的生成树数量。
***
由 Prufer 序列和无根树的**双射关系**,不难发现答案就是 $n^{n-2}$。
***
例题 $3$:([CF156D Clues](https://www.luogu.com.cn/problem/CF156D))给定一个 $n$ 个点 $m$ 条边的带标号无向图,它有 $k$ 个连通块,求添加 $k-1$ 条边使得整个图连通的方案数,答案对 $p$ 取模。
***
由于我们不知道度数,所以我们直接把度数数组 $d$ 设出来。记 $d_i$ 为连通块 $i$ 的度数,根据 Prufer 序列性质 $3$,我们考虑每个度数在 Prufer 序列中的位置。于是有如下式子。
$$\binom{k-2}{d_1-1,d_2-1,\dots,d_n-1}=\frac{(k-2)!}{(d_1-1)!(d_2-1)!\dots(d_k-1)!}$$
对于第 $i$ 个连通块,它的连法有 $d_i$ 种,累乘进去。
$$\binom{k-2}{d_1-1,d_2-1,\dots,d_k-1}\prod_{i=1}^ks_{i}^{d_i}$$
考虑多元二项式定理。
$$(x_1+x_2+\dots+x_m)^p=\sum_{c_i\ge0,\sum_{i=1}^mc_i=p}\binom{p}{c_1,c_2,\dots,c_m}\prod_{i=1}^mx_i^{c_i}$$
于是我们考虑进行一个元的换,令 $e_i=d_i-1$,不难发现 $\sum d_i$ 是边数的两倍,所以 $\sum d_i=2k-2$,于是 $\sum e_i=k-2$,考虑写成多元二项式定理的形式。
$$\sum_{e_i\ge0,\sum_{i=1}^me_i=k-2}\binom{k-2}{e_1,e_2,\dots,e_k}\prod_{i=1}^ks_i^{e_i+1}$$
把 $s_i^{e_i+1}$ 拆成 $s_i^{e_i}s_i$,于是有如下式子。
$$\sum_{e_i\ge0,\sum_{i=1}^me_i=k-2}\binom{k-2}{e_1,e_2,\dots,e_k}\prod_{i=1}^ks_i^{e_i}\prod_{i=1}^ks_i$$
直接使用多元二项式定理。
$$(s_1+s_2+\dots+s_k)^{k-2}\prod_{i=1}^ks_i$$
注意到 $s_1+s_2+\dots+s_k=n$,就推出了最后的式子。
$$n^{k-2}\prod_{i=1}^ks_i$$
### Polya 定理
对于**集合** $G$ 和**二元运算** $*$,如果满足以下四条性质,则将集合 $G$ 和二元运算 $*$ 称为一个群。
$1$:(**封闭性**) $\forall x,y\in G,x*y\in G
2$:(**结合律**) $\forall x,y,z\in G,(x*y)*z=x*(y*z)
3$:(**存在单位元**) $\exist e\in G\;\forall x\in G,x*e=e*x=x
4$:(**存在逆元**)$\forall x\in G\exist x^{-1}\in G,x*x^{-1}=x^{-1}*x=e
一个群具有如下几条性质。
1$:(**单位元唯一**)$e_1e_2=e_1=e_2
$3$:(**逆元唯一**)对于每一个元素 $x$,有且仅有一个 $x^{-1}$ 使 $xx^{-1}=e
置换 $\binom{1,2\dots n}{a_1,a_2\dots a_n}$ 可以被写作 $(1,a_1,a_{a_1}\dots)\dots(\dots)$ 的形式,称为置换的**循环表示**。其中 $(a_1a_2\dots a_m)$ 被称为一个 **$m$ 阶循环**。
***
([【模板】Polya 定理](https://www.luogu.com.cn/problem/P4980))给定一个 $n$ 个点,$n$ 条边的环,有 $n$ 种颜色,给每个顶点染色,问有多少种不能通过旋转与别的染色方案相同的染色方案。
***
如果一个对象在置换后**没有变化**,那我们把这个元素称为**置换不动点**。
对于一个置换群计数,**方案个数**等于**置换不动点的平均值**,这就是 **Burnside 引理**。可以表示为下面式子,其中 $\mid X\mid$ 为最后计数的答案,$c(g)$ 表示置换 $g$ 下不动点的数量,$\mid G\mid$ 表示置换的总数量。
$$\mid X \mid=\frac{\sum c(g)}{\mid G\mid}$$
对于 $c(g)$,我们可以把置换 $g$ 用**循环**表示写出来,统计其中 **$i$ 阶循环**的个数 $c_i$,对于每一阶循环存在一个 $x_i$,$c(g)=\prod_ix_i^{c_i}$。**Polya 定理**指出,在**染色问题**的循环同构计数中,若染色数量为 $m$,则 $x_1=x_2=\dots x_n=m$。
对于本题,我们直接套公式就行了。手玩一下,发现顺时针旋转 $i$ 个元素会带来 $\gcd(n,i)$ 个循环,总共有 $n$ 种旋转方法,对应 $n$ 个置换,把公式直接套进去。
$$\frac{1}{n}\sum_{i=1}^nn^{\gcd(n,i)}$$
然后进行大力反演,暴力计算欧拉函数即可。时间复杂度 $O(t\sqrt{n\sqrt{n}})$。
$$\frac{1}{n}\sum_{d\mid n}n^d\sum_{i=1}^{\frac{n}{d}}[\gcd(\frac{n}{d},i)=1]=\frac{1}{n}\sum_{d\mid n}n^d\varphi(\frac{n}{d})$$
另外,$x_1,x_2\dots x_n$ 的本质实际上是一种**生成函数状物**。例如,有 $3$ 种颜色,每种必须恰好用两个,我们就令 $x_i=a^i+b^i+c^i$,最后的方案数就是 $a^2b^2c^2$ 项的系数。
### 矩阵树定理
***
([【模板】Matrix-Tree 定理](https://www.luogu.com.cn/problem/P6178))给定一张 $n$ 个结点 $m$ 条边的带权图(可能为无向图,可能为有向图)。定义一棵生成树的权值为其所有边的权值之积,求其所有不同生成树的权值之和。
***
首先学习一下**行列式**科技。一个 $n$ 行 $n$ 列的方阵 $A$ 的行列式定义为 $\det(A)$,可以通过如下计算式求出。
$$\det(A)=\sum_p(-1)^{\tau(p)}\prod_{i=1}^na_{i,p_i}$$
其中 $p$ 是一个**排列**,$\tau(p)$ 是排列 $p$ 中的**逆序对**个数。
注意到这么计算时间复杂度是 $O(n!n)$ 的,无法接受。考虑行列式的性质。
$1$:**交换**矩阵两行(或两列),行列式**取反**。
$2$:把某一行(或一列)**加上**另一行(或一列)每个元素**乘以**一个**常数**,行列式**不变**。
$3$:**行列式展开定理**
$$\det(A)=\sum_{i=1}^na_{x,i}(-1)^{x+i}M_{x,i}$$
其中 $x$ 是想要展开的行,$M_{x,i}$ 表示 $A$ 居正删去第 $x$ 行和第 $i$ 列后形成的矩阵的行列式。
我们使用类似**高斯消元**的方法把矩阵消成一个**上三角矩阵**,然后发现行列式的值就是**对角线**上所有值乘起来。高斯消元的过程中,可以使用**辗转相减法**,时间复杂度 $O(n^3+n^2\log n)$。
**邻接矩阵**:$e[i][j]$ 表示 $i\to j$ 的所有连边的**权值之和**,没有权值则默认权值为 $1$。
**度数矩阵**:这个矩阵**只有 $a_{i,i}$ 有值**且值为**点 $i$ 的度数**,即与 $i$ 相连的边的**权值和**。其余点均为 $0$。
然后就是矩阵树定理。对于**无向图**,我们用**度数矩阵减去邻接矩阵**,去掉**任意**第 $i$ 行和第 $i$ 列求行列式,就是无向图的**生成树数量**。
对于**有向图**,度数矩阵分为**入度矩阵**和**出度矩阵**。**入度矩阵减去邻接矩阵**去掉一行一列求出来的是**外向生成树数量**,**出度矩阵减去邻接矩阵**去掉一行一列求出来的是**内向生成树数量**,去掉第 $i$ 行和第 $i$ 列表示生成树的**树根是 $i$**。
然后换成边的权值之积,其实就是把权值为 $w_i$ 的边加 $w_i$ 次,这在邻接矩阵和度数矩阵上都是容易做到的。
***
([[省选联考 2020 A 卷] 作业题](https://www.luogu.com.cn/problem/P6624) 子问题)给定一张 $n$ 个结点 $m$ 条边的无向带权图。定义一棵生成树的权值为其所有边的权值之和,求其所有不同生成树的权值之和。
***
考虑矩阵树定理只能进行乘法,我们考虑**生成函数化**,把权值为 $w_i$ 的边加一个一次式 $w_ix+1$ 次,经过矩阵树定理的乘法运算,你发现**一次项系数**刚好是生成树的权值和,然后就做完了。
### K-D Tree
***
([简单题](https://www.luogu.com.cn/problem/P4148))给定 $n\times n$ 的二维平面,支持单点加,矩形求和。空间复杂度 $O(n)$,强制在线。
***
K-D Tree 是一种神奇的类 BST 数据结构,用于维护**高维信息**。使用二进制分组优化的 K-D Tree 复杂度为插入 $O(n\log^2 n)$,查询 $O(\sqrt{n\log n}+n^{1-\frac{1}{k}})$,其中 $k$ 为维度数。
先考虑对于一个固定的点集建立 K-D Tree。我们维护高维空间内的若干个点。我们每次按照深度**轮流**选择维度,每次按照**中位数**进行划分,得到左右两个子树**分别递归**处理。可以使用 **`nth_element`** 在 $O(n)$ 的时间内完成这个划分并排序的过程。不难发现,这时 K-D Tree 的**树高**是 $O(\log n)$ 级别的。
考虑**插入**一个数,可能会造成 K-D Tree 不再平衡。而 K-D Tree 没有什么好的性质,既不能像 Splay 一样旋转,也不能像 FHQ 一样随即优先级,而像替罪羊树一样定期重构会被叉爆。因此,我们考虑一些基于**合并**的插入方式。
我们维护 $p$ 棵**大小为 $2^i(0\le i\le p)$** 的 K-D Tree,每次插入时创建一棵大小为 $1$ 的 K-D Tree,如果有大小相同的 K-D Tree,就暴力**拍扁合并**。总时间复杂度 $O(n\log^2 n)$。实际写代码时,可以一直拍扁,存进同一个数组里,最后建一次树。
考虑查询。如果访问到**空节点**或**无交集**的节点,直接**返回**。如果**完全包含**,直接**返回**。否则如果当前节点**代表的点被包含**就**更新**,否则就**不更新**。然后**递归**左右子树更新。
于是这个题就显然了,维护一个二维 K-D Tree 就做完了。
***
([[CH弱省胡策R2] TATT](https://www.luogu.com.cn/problem/P3769))求四元最长不下降子序列的长度。
***
K-D Tree 优化 DP。先排序消掉第一维,然后三维 K-D Tree 直接莽,把每一个 DP 值插进去,转移时查询就行了。
注意到,在 THUWC 赛场上某英文名 R 开头 R 结尾的同学使用 $O(n^{\frac{5}{3}})$ 的三维 K-D Tree 通过了 $5\times 10^5$ 的数据,打爆了 $O(n\log^2 n)$ 的二维线段树,我们要充分发扬这个精神。
### Mex 科技
若区间 $[l,r]$ 的区间 $\text{mex}=c$,当且仅当**不存在**区间 $[l',r']\subset[l,r]$ 使得区间 $[l',r']$ 的区间 $\text{mex}=c$,我们称区间 $[l,r]$ 为**极短 $\text{mex}$ 区间**,记作极短 $\text{c-mex}$ 区间。
对于所有的 $c$,我们断言,极短 $\text{mex}$ 区间的**总数在 $O(n)$ 级别**。可以使用构造性证明,参考 [这篇题解](https://www.luogu.com.cn/article/w27c2vd6)。
考虑怎么把极短 mex 区间求出来。极短 $\text{0-mex}$ 区间和极短 $\text{1-mex}$ 区间是好求的。假设我们知道了极短 $\text{(c}-\text{1)-mex}$ 区间,考虑求 $\text{c}$ **更大**的极短 $\text{c-mex}$ 区间。
根据构造性证明,极短 $\text{c-mex}$ 区间一定由 $\text{c}$ **较小**的极短 $\text{c-mex}$ 区间左右之一**扩展**而来。于是,我们顺序遍历 $1\sim n$,每次把极短 $\text{i-mex}$ 区间分别**向左**或**向右**扩展到**第一个** $i$ 出现的位置,并将这些区间记为对应区间 mex 的极短 $\text{c-mex}$ 区间。这样**一定**会统计所有极短 $\text{c-mex}$ 区间,但可能一些区间**不是**极短的,需要排序后**去除**。区间查询 $\text{mex}$ 可以使用**主席树**查询第一个上次出现位置小于 $l$ 的数实现。
之后,对于**每一个**极短 $\text{c-mex}$ 区间 $[l_1,r_1]$,都存在一个**极长 $\text{c-mex}$ 区间** $[l_2,r_2]$,由极短 $\text{c-mex}$ 区间**向左且向右**扩展到第一个 $c$ 出现的位置。对于区间 $[l,r]$,如果 $l_2\le l\le l_1,r_1\le r\le r_2$,则有这个区间的 **$\text{mex}$ 值为 $c$**。于是我们就把问题转化到了**二维平面**上**矩形信息**维护问题。
***
([[THUPC 2024 初赛] 套娃](https://www.luogu.com.cn/problem/P9970))给定序列 $a$,对于每一个 $1\le k\le n$,求所有长度为 $k$ 的子区间的 $\text{mex}$ 的 $\text{mex}$。
***
考虑直接使用 Mex 科技,注意到一个矩形的贡献是连续的,为 $[r_1-l_1+1,r_2-l_2+1]$,差分后使用 `set` 维护没有出现过的数插入删除查最小值即可。时间复杂度 $O(n\log n)$。
### Pollard-Rho
***
给定一个数 $n$,把 $n$ 进行质因数分解。
$O(n^{\frac{1}{4}}\log^2 n)
首先我们有费马小定理的逆定理 ,若 x^{p-1}\equiv1\pmod p ,则 p 为素数。这显然是错的。
然后我们有二次探测定理 ,若 p 为奇素数 ,则 x^2\equiv 1\pmod p 的解有且仅有 x\equiv 1\pmod p 或 x\equiv -1\pmod p 。
于是我们有 Miller-Rabin 算法 。假设有 x^{p-1}\equiv1\pmod p ,变形一下有 (x^{\frac{p-1}{2}})^2\equiv1\pmod p ,根据二次探测定理有 x^{\frac{p-1}{2}}\equiv1\pmod p 或 x^{\frac{p-1}{2}}\equiv-1\pmod p 。如果出现前者我们继续递归,否则直接认为通过检验。特别的,如果指数为奇数,不能继续递归,直接认为通过检验。
具体实现的时候,我们可以先把指数除到奇数,然后从底向上快速幂把每一位的结果求出来,再从顶到底判定,时间复杂度 O(\log n) 。
如果我们取前 12 个素数作为底数验证,可以适用于 2^{78} 内的判素。
考虑快速求出一个数 x 的任意一个因子 ,我们使用随机化 。我们随机 一个数 d ,假设上一个数为 k ,我们令 k'=(k^2+d)%x ,然后计算 \gcd(\mid k'-k\mid,x) 。如果不为 1 ,就找到了一个因子。至于为什么这么做可能是有人算出来这样正确率较高吧。
然后有一个小优化。为了节省 \gcd 的时间,我们把 k'-k 累乘 起来,然后倍增 算 \gcd 。先 1 次累乘算 1 次 \gcd ,再 2 次累乘算 1 次 \gcd ,直到达到上界 k 次累乘算 1 次 gcd ,这个 k 一般取 127 。这就是 Pollard-Rho 算法 ,期望时间复杂度 O(n^{\frac{1}{4}}) 。
然后考虑如何分解质因数 。我们每次找出一个因子,用队列 维护。如果这个因子是质数 ,加入质因子队列,否则找出其一个因子继续分解 。遍历直到这个队列为空即可。
倍增值域分块
固定路径和初始值 x ,每个节点二元点权 (x_i,y_i) ,在每个节点处 x 和 x_i 比较大小,如果大于就加上或减去 x_i ,否则加上或减去 y_i 。
预处理 O(n\log n\log V) ,查询 O(\log n\log V) ,单点修改 O(\log n\log V) 。
考虑把值域分成 [2^{k-1},2^k) 若干个块,把小于这个块的元素称为轻元素 ,大于等于这个块的元素称为重元素 。当前元素有且仅有两种方法离开这个块,一种是取到一个重元素 ,另一种是一直取轻元素 。
我们可以分别维护出这两种情况出现的位置,取最小值 直接跳。可以对每个块倍增 维护,对每个块线段树 可以做到单调修改 。具体的,我们的数据结构维护轻元素的和 和重元素与其之前的轻元素的和的最小值 ,可以线段树类似分治维护。这个块一般开到序列中的最大值域,如果初始值在倍增过程中大于最大值域按最大块计算。注意此时不会出现只取轻元素到下一个块。
可以把块的底数 修改达到平衡复杂度 ,例如,以 [4^{k-1},4^k) 分块,其余不变,预处理常数减半,询问时间增加约 50\% 。
线段树分治
学习资料
每个操作只在 [l,r] 的时间段内有效,询问某一个时间点所有操作的贡献。
***
对于这样的询问,我们可以**离线**后在**时间轴**上建一棵线段树,这样对于每个操作,相当于在线段树上进行**区间操作**,在操作的区间打上标记,相当于**标记永久化**。
离线后遍历**整棵线段树**,到达每个节点时执行**相应的操作**,然后继续**向下递归**,到达**叶子节点**时**统计贡献**,**回溯**时**撤销操作**即可。
这样的思想被称为**线段树分治**,可以在低时间复杂度内解决一类在线算法并不优秀的问题。
***
([【模板】线段树分治](https://www.luogu.com.cn/problem/P5787))一张图有 $n$ 个节点的图,在 $k$ 时间中会出现 $m$ 条边,表示有一条连接 $x,y$ 的边在 $l$ 时刻出现 $r$ 时刻消失,求问在第 $i$ 个时间段中图是否为二分图。
***
先线段树分治。考虑操作怎么维护,使用扩展阈并查集,把每个点拆成两个状态,每次连边把 $x$ 状态 $1$ 和 $y$ 状态 $2$ 连边, 把 $x$ 状态 $2$ 和 $y$ 状态 $1$ 连边。如果某个节点两个状态在同一个连通块中, 说明无法给这张图染色,有奇环,这张图就不是二分图。撤销的话直接使用可撤销并查集即可。时间复杂度 $O(n\log^2n)$。
注意叶子节点访问结束也要撤销,这是一个经常写错的地方。
### exKMP
***
给定字符串 $b$,求 $b$ 的每一个后缀 $i$ 与 $b$ 的最长公共前缀长度 $z[i]$ 。
$O(\mid a\mid+\mid b\mid)$。
***
考虑 Manancher 的思想,从 $1\to n$ 依次递推。假设我们正在计算 $z[i]$,且 $\forall j\lt i$ 的 $z[j]$ 已求出。本文中下标以 $1$ 开始,$j$ 是 $\lt i$ 的满足 $j+z[j]$ 的值最大的 $j$。
$1$:最理想的情况
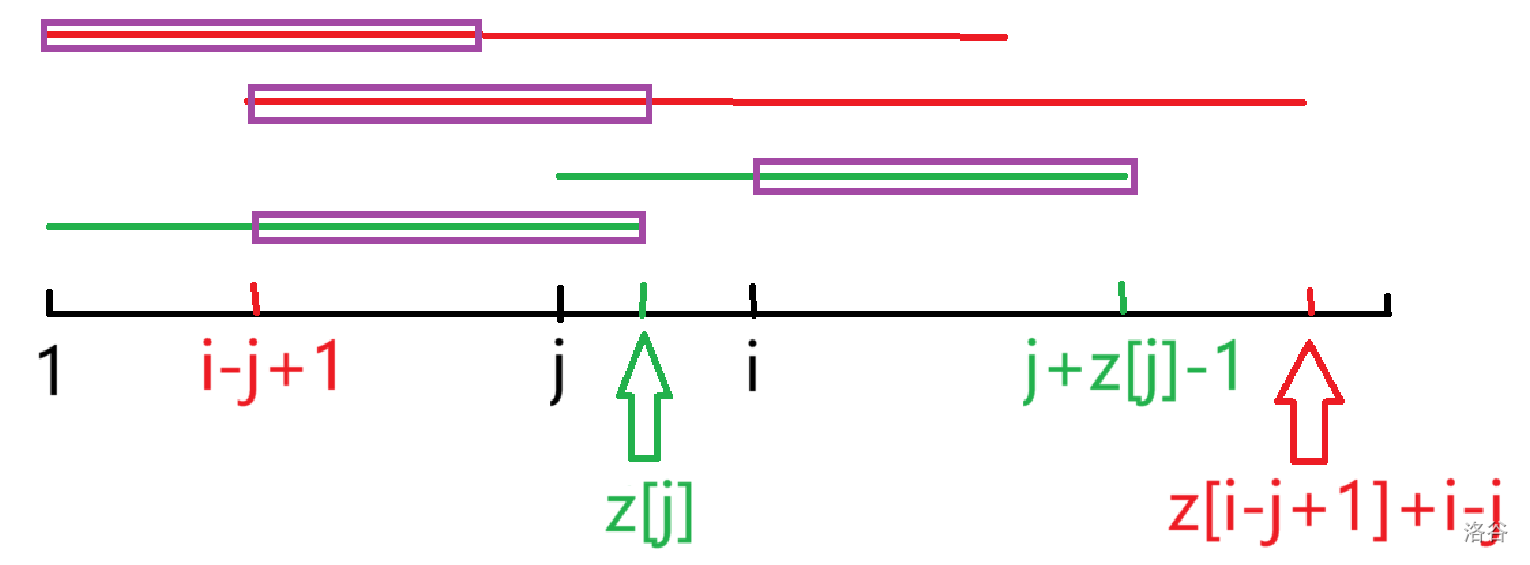
此时 $z[i-j+1]\ge z[j]+j-i$,即 $z[i-j+1]+i-j\ge z[j]$,说明紫色的这几段全部相等,而后面的我们不知道,因此有 $z[i]=z[j]+j-i$,然后暴力往后扩展。
由于扩展后 $i+z[i]$ 会大于 $j+z[j]$,$j$ 会更新为 $i$ 导致 $j+z[j]$ 增加,所以每个数只会被暴力遍历一次,$j+z[j]$ 单调不降,时间复杂度 $O(n)$。
$2$:不是很理想的情况

此时 $z[i-j+1]\lt z[j]+j-i$,即 $z[i-j+1]+i-j\lt z[j]$,说明上一种情况中紫色段一定不相等,否则 $z[i-j+1]$ 还可以扩展。因此,此时 $z[i]$ 的值一定等于这种情况图中的紫色段长度,即 $z[i-j+1]$,不需要继续扩展。
$3$:很不理想的情况
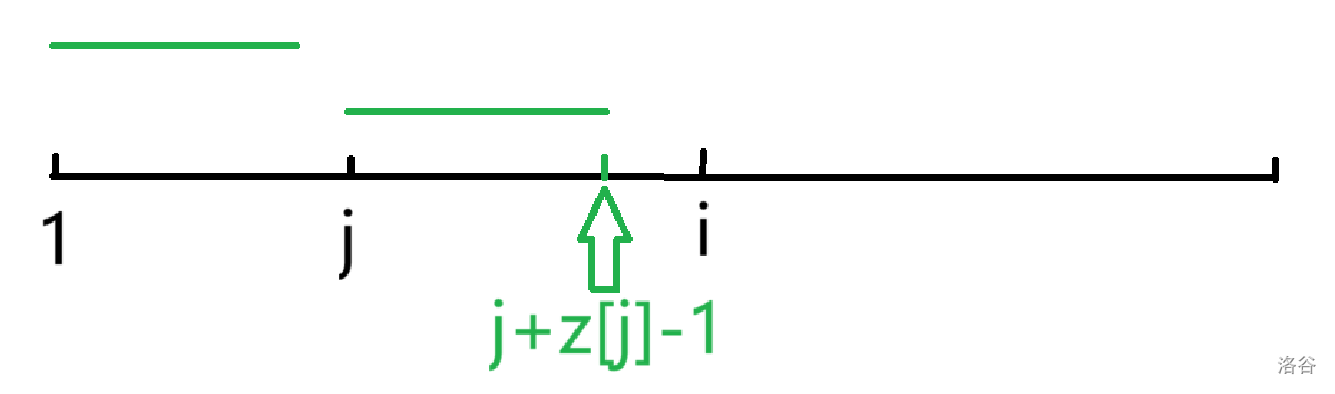
此时有 $j+z[j]\lt i$,但没有一点信息可以利用,直接暴力扩展,由于还是会更新 $j+z[j]$ 的最大值,所以复杂度依旧是 $O(n)$。
~~欸这不就是 [Manacher](https://www.luogu.com.cn/article/qup16nwq) 吗?~~
***
([【模板】exKMP](https://www.luogu.com.cn/problem/P5410))给定两个字符串 $a,b$,求 $b$ 与 $a,b$ 两个字符串的每一个后缀的最长公共前缀。
***
把 $a$ 拼在 $b$ 后面,然后跑一遍 exKMP,然后把属于 $b$ 的后缀对这个后缀长度取 $\min$,属于 $a$ 的后缀对 $b$ 数组长度取 $\min$ 即可。
### 最小树形图
***
([【模板】最小树形图](https://www.luogu.com.cn/problem/P4716))给定有向图,求这棵有向图以 $rt$ 为根的外向最小生成树。
$O(nm)
我们可以通过朱刘算法 解决最小树形图问题。
我们首先对除 rt 外每个结点选择一条最短的入边 ,将边权加到答案中。这样做之后的图由到根的 DAG 和若干棵内向基环树 组成。通过某种方式找到环,我们把环上的点缩点 ,环上的点不在环上的边的边权减去 环上的边的边权。这相当于反悔贪心 ,选择另一条入边时撤销 的贡献。
具体写的时候直接存边,记录每个点在哪个环,修改边的两端点。减掉某条边贡献可以直接对所有点减终点节点的最小入边权值。因为如果不是最小入边符合要求,如果是,若在环上会被缩没,若不在环上边权变为 0 ,相当于确定了要选这条边。
并查集判环时间复杂度 O(nm\log n) ,可以接受。
Hall 定理
假设 G=(X,Y,Z) 是二分图 ,且 \lvert X\rvert\le\lvert Y\rvert 。对于一个图的匹配 M ,若 X 中的所有 点都是匹配点,那么称 M 是一个完美匹配 。
在这个二分图中,如果对于任何 W\subseteq X ,与 W 中的点直接相连 的点的集合大小大于等于 W 的集合大小,则这个二分图存在完美匹配 。反之亦然。
([POI 2009] LYZ-Ice Skates)给定一个二分图,每种右部点有 k 个,左部点初始为空。左部点 x 可以匹配 [x,x+d] 中的右部点。动态修改某种左部点 r(1\le r\le n-d) 数量,每次求是否存在完美匹配。
考虑对每个右部点记录一个 p 表示可以承载多少对应位置的左部点,初始为 -k ,修改时直接增加或删除。根据 Hall 定理,我们找到限制最紧的集合,即最大子段和。如果这个最大子段和 \gt k\times d ,证明算上 [x+1,x+d] 这些位置的点也不够,不满足 Hall 定理,无解。否则有解。
DP 套 DP
DP 套 DP 是把另一个 DP 过程 (一般是某一个状态 )当作状态 进行 DP 的 DP。DP 套 DP 的难点一般在于如何寻找可以刻画 的内部 DP 的状态,从而进行转移。
DP 套 DP 一般数据范围不会太大,而且一般是计数题。
([ROI 2012 Day 2] army 汗国军队)给定 n 阶排列的一个最长上升子序列,求这样的排列的个数。
考虑 DP 套 DP。最长上升子序列的常规做法很难刻画,考虑最长上升子序列的另一种求法:维护 f_i 表示长度 i 的 LIS 结尾数最小值,这个数组是单调递增的,每新加一个数进来,修改第一个大于这个数的位置,如果没有就使 LIS 长度加 1 接到最后。
考虑外层 DP 是每次插入一个数,而这个刻画方式可以使得每个数要么在 f_i 中,要么曾经在过又被踢出去了,要么还没有考虑,因此我们可以使用三进制状态压缩记录内层 DP 状态。直接转移即可,常熟很小,O(n^23^n) 也能过。
BEST 定理
定义两个欧拉回路不相等当且仅当它们循环不同构,求一张 n 个点的有向图的欧拉回路个数。
***
对于这种问题,我们考虑 **BEST 定理**。
$$\text{euc}(G,k)=t^{\text{in}}(G,k)\prod_{v\in V}(\deg^{\text{ou}}(v)-1)!$$
其中 $V$ 为图 $G$ 的点集,$\text{euc}(G,k)$ 表示以 $k$ 为**起点**的**非循环同构**欧拉回路**个数**,$t^{\text{in}}(G,k)$ 表示图 $G$ 以点 $k$ 为根的**内向生成树个数**,可以通过**矩阵树定理**求出,$\deg^{\text{ou}}(v)$ 为点 $v$ 的**出度**。
实际运用时不需要特别区分入度和出度,因为根据**有向图欧拉回路存在定理**,如果存在欧拉回路,则所有点的入度和出度**相等**。
特别注意,如果题目需要求的数量认为**循环不同构**,则需要**乘上** $\deg^{\text{ou}}(k)$ 才是最后的答案。
***
([[USACO21OPEN] Routing Schemes P](https://www.luogu.com.cn/problem/P7531))给定一张无向图,存在 $s$ 个源点和汇点,求源点和汇点两两匹配且所有路径中每条边恰好使用一次的方案数。
***
恰好使用一次提示欧拉回路,考虑加入一个超级源点 $s$,$s$ 连向所有源点,且所有汇点连向 $s$,这个图中的欧拉回路等价于原图中的一个方案。但直接用 BEST 定理数出的数量会算重 $s$ 连的边的贡献,于是我们在 $\text{euc}(G,s)$ 中除掉 $(\deg^{\text{ou}}(s)-1)!$,不是 $\deg^{\text{ou}}(s)!$ 是因为数出的欧拉回路循环同构。
### Wavelet Matrix
***
([【模板】可持久化线段树 2](https://www.luogu.com.cn/problem/P3834))静态区间第 $k$ 小问题。时间 $O(n\log n)$,空间 $O(\frac{n\log n}{w})$。
***
[学习资料](https://zhuanlan.zhihu.com/p/590974585)
Wavelet Matrix,波纹疾走算法是下面这样的结构。
首先,我们把原数组的二进制最高位(这里认为是第 $29$ 位)找出来,把这些位的值记作 $b_{29}$,按这一位进行稳定排序。排序后,我们再把第 $28$ 位找出来,把这些位的值记作 $b_{28}$,继续按这一位进行稳定排序,直到记录 $b_0$。
我们发现这本质上就是一个 01-Trie 的结构,因此这个结构也能支持类似的操作,但可以支持一些位置信息。
例如,查询位置 $l$ 的值,我们考虑在每一次的稳定排序的过程中利用 $b$ 找出下一次 $l$ 的位置。假设现在在 $b_x$,如果这一次 $b_{x,l}=0$,由于稳定排序,则在下一层的 $b$ 中 $l$ 会映射到等同于 $b_x$ 中 $[1,i]$ $0$ 的个数的位置。如果这一次 $b_{x,l}=1$,由于稳定排序,则在下一层的 $b$ 中 $l$ 会映射到等同于 $b_x$ 中 $0$ 的个数加上 $[1,i]$ $1$ 的个数的位置,并将答案累加一个 $2^{x}$。
我们可以感受到 Wavelet Matrix 是一个利用稳定排序的位置性来在处理值域的过程中保留位置信息的数据结构,因此我们尝试解决静态区间第 $k$ 小问题。
假设我们查询的区间是 $[l,r]$,那我们可以根据 $[l,r]$ 中 $0$ 的个数来确定第 $k$ 小这一位是 $0$ 还是 $1$。记前缀 $x$ 中 $0$ 的个数为 $c_{0,x}$,$1$ 的个数为 $c_{1,x}$,如果是 $0$,那下一个区间就是 $[c_{0,l-1}+1,c_{0,r}]$;如果是 $1$,那下一个区间就是 $[c_{0,n}+c_{1,l-1}+1,c_{0,n}+c_{1,r}]$,累加 $2^x$ 的贡献,并且由于我们踢掉了 $[l,r]$ 中 $0$ 的个数的数,$k$ 也要相应减小。
$b_x$ 的各种信息可以使用手写 `bitset` 维护,即可做到时间 $O(n\log n)$,空间 $O(\frac{n\log n}{w})$。写代码的时候需要注意存进 `bitset` 中时要将下标转换为从 $0$ 开始,以及 `1ull<<(63+1)` 会导致 UB 需要特判。
还有很多别的应用没有记录。
### 长链剖分优化 DP
长链剖分与重链剖分类似,只不过将重儿子改为了深度最深的长儿子。由于 $1+2+\dots+n$ 是 $O(n^2)$,因此长链条数为 $O(\sqrt{n})$,这导致长链剖分在 DS 上没有什么应用。
长链剖分的经典应用除了 $O(1)$ 求树上 $k$ 级祖先之外,还有一个重要应用就是优化 DP。
长链剖分优化 DP 的关键在于一条长链可以存储一个子树内所有与深度有关的信息,因此当我们遇到和深度有关的 DP 时,可以先对长儿子做 DP,然后把其他儿子的 DP 值暴力合并到长儿子的 DP 值。由于每条重链只会被合并一次,因此时空复杂度都是 $O(n)$ 的。
长链剖分优化 DP 时需要注意不能预先把内存开好,需要先开一个内存池,用指针分配内存。转移式涉及到深度整体变化的,可以直接偏移指针解决。具体可以看代码实现。
一个经典例题是 [CF1009F Dominant Indices](https://www.luogu.com.cn/problem/CF1009F)。