矩阵的前世今生(别看,是作业
Cyancer
·
·
个人记录
1.矩阵的定义
在数学中,矩阵(Matrix)是一个按照长方阵列排列的复数或实数集合,最早来自于方程组的系数及常数所构成的方阵。这一概念由19世纪英国数学家凯利首先提出。
由 m * n 个数a _i _j 排成的 m 行 n 列的数表称为 m 行 n 列的矩阵,简称 m × n 矩阵。
A=\left[ \begin{matrix}a & b & ... & c\\ d & e & ... & ... \\ ... & ... & ... & ... \\ f & ... & ... & g \end{matrix} \right]
这 m × n个数称为矩阵A的元素,简称为元,数 a _i _j 位于矩阵A的第 i 行第 j 列,称为矩阵 A 的 ( i , j ) 元,以数a _i _j 为 ( i , j )元的矩阵可记为 a _i _j 或( a _i _j ) _m _× _n , m × n 矩阵 A 也记作 A _m _n 。
如果 A 与 B 都为 m × n 的矩阵,那么 A 与 B 互为同型矩阵。
另外,1 * m 的矩阵又叫向量。
2.矩阵的历史背景与发展
根据世界数学发展史记载,矩阵概念产生于19世纪50年代,是为了解线性方
程组的需要而产生的。
然而,在公元前我国就已经有了矩阵的萌芽。在我国的《九章算术》一书中
已经有所描述,只是没有将它作为一个独立的概念加以研究,而仅用它解决实际
问题,所以没能形成独立的矩阵理论。
1850年,英国数学家西尔维斯特 (SylveSter,1814--1897)在研究方程的个
数与未知量的个数不相同的线性方程组时,由于无法使用行列式,所以引入了矩
阵的概念。
1855年,英国数学家凯莱 (Caylag,1821--1895)在研究线性变换下的不变
量时,为了简洁、方便,引入了矩阵的概念。1858年,凯莱在《矩阵论的研究报
告》中,定义了两个矩阵相等、相加以及数与矩阵的数乘等运算和算律,同时,
定义了零矩阵、单位阵等特殊矩阵,更重要的是在该文中他给出了矩阵相乘、矩
阵可逆等概念,以及利用伴随阵求逆阵的方法,证明了有关的算律,如矩阵乘法
有结合律,没有交换律,两个非零阵乘积可以为零矩阵等结论,定义了转置阵、
对称阵、反对称阵等概念。
1878年,德国数学家弗罗伯纽斯 (Frobeniws,1849一1917)在他的论文中引
入了λ 矩阵的行列式因子、不变因子和初等因子等概念,证明了两个λ 矩阵等价
当且仅当它们有相同的不变因子和初等因子,同时给出了正交矩阵的定义,1879
年,他又在自己的论文中引进矩阵秩的概念.
矩阵的理论发展非常迅速,到19世纪末,矩阵理论体系已基本形成。到20
世纪,矩阵理论得到了进一步的发展。目前,它己经发展成为在物理、控制论、
机器人学、生物学、经济学等学科有大量应用的数学分支
(择自张力宏编高等代数)
3.矩阵的基本运算
1.矩阵加法
两个矩阵相加,必须满足两个矩阵都为 m × n 的矩阵(即同型矩阵),因为矩阵运算已经不单单只是数与数之间的运算,而是集合与集合之间的运算而集合与集合之间的运算最重要的一点就是两个集合的元素个数必须相等
eg1.
另外,矩阵加法满足以下运算律:
1.交换律
A+B=B+A
2.结合律
(A+B)+C=A+(B+C)
2.矩阵减法
和加法类似,也是必须满足两个矩阵都为同型矩阵
eg2.
另外,矩阵减法也满足以下运算律:
A+B=B+A
2.结合律
(A+B)+C=A+(B+C)
3.数乘矩阵
数乘矩阵,顾名思义,用一个数量去乘以一个矩阵,其实就是将这个矩阵的元素大小扩大这个数量倍
eg3.
另外,数乘矩阵满足以下运算律:
1.交换律
a(bA)=b(aA)
2.结合律
a(bA)=(ab)A
3.(左右)分配律
a(A+B)=aA+aB
(a+b)A=aA+bA
以上三点合称矩阵的线性运算
4.转置
将矩阵A的行与列交换所得到的的新矩阵被称为矩阵A的转置矩阵,即A^T
eg.4
另外,转置满足以下规律(因为已经不是运算律了):
1.
2.
3.(这个涉及到矩阵乘法,建议先看下面的矩阵乘法再看这个)
5.共轭
共轭的定义:
两个实部相等,虚部互为相反数的复数互为共轭复数(conjugate complex number)。(当虚部不等于0时也叫共轭虚数)复数z的共轭复数记作 \bar{z} (z上加一横,英文中可读作Conjugate z,z conjugate or z bar),有时也可表示为z*。
即
若有
z=a+bi
则有
简单的说就是两个变量互为相反数的的数就互为共轭复数 。
**共轭矩阵**:
共轭矩阵又称Hermite矩阵,在共轭矩阵中任意第i行第j列的元素都与第j行第i列的元素的共轭相等
即
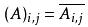
**eg.5**
若有
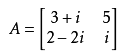
则有
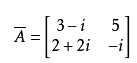
**6.共轭转置**
字面意思,就是先把矩阵转置后,再把每一个数换成它的共轭复数。
即
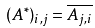
或写作
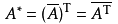
**eg.6**
若有
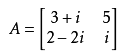
则有
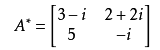
------------
### 4.矩阵乘法
随着矩阵的不断发展与进步,在矩阵最与众不同,也是最复杂的一方面:矩阵乘法上,也有着数代的发展与变化,由此衍生出了许许多多的不同的矩阵乘法,以下是部分我所总结的矩阵乘法。
#### 1.普通的矩阵乘法
**首先**
如果要使两个矩阵的相乘有意义,那么第一个矩阵的行数必须等于第二个矩阵的列数,即必须是一个 m × q 的矩阵去乘一个 q × n 的矩阵
**定义**
设A为 m × q 的矩阵,B为 q × n 的矩阵,那么称 m × n 的矩阵**C**为矩阵**A**与**B**的乘积,记作 _**C**=**AB**_ ,其中**矩阵C**中的第 _i_ 行第 _j_ 列元素可以表示为:
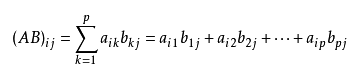
即
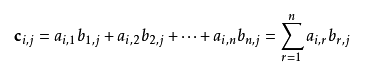
并将此乘积记为 _**C**=**AB**_
**eg.7**
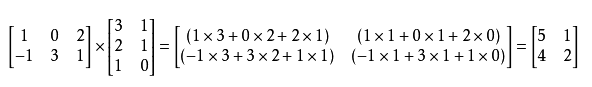
另外,矩阵乘法满足以下运算律:
**1.结合律:**
_(AB)C=A(BC)_
_a(AB)=(aA)B=A(aB)_
**2.(左右)分配律**
_(A+B)C=AC+BC_
_A(B+C)=AB+AC_
#### 2.乘积-哈达马积(Hadamard product)
_m*n_ 的矩阵 _A_ 与 _m*n_ 的矩阵 _B_ 的哈达马积记为 _A*B_ , _A*B_ 也是一个 _m*n_ 的矩阵,其各个元素的定义为两个矩阵对应元素的乘积
即
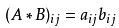
**eg.8**
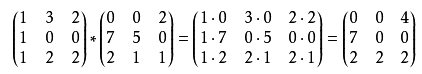
**性质**
哈马达积满足以下运算律:
**1.交换律**
_A * B=B * A_
**2.结合律**
_A * (B * C)=(A * B) * C_
**3.左分配律**
_A * (B + C)=A * B + A * C_
#### 3.乘积-克罗内克乘积(Kronecker product)
_m × n_ 的矩阵 **_A_** 与 _p × q_ 的矩阵 _B_ 的克罗内克乘积记为 _A $\bigotimes$ B_ , _A $\bigotimes$ B_ 是一个 _mp*nq_ 的矩阵,克罗内克乘积也被称为直积或张量积。
可具体的表示为
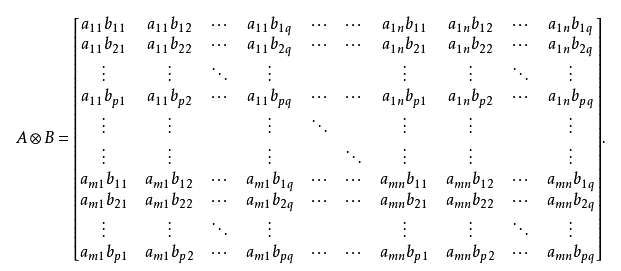
**eg.8**

**性质**
克罗内克乘积满足以下性质:
**1.双线性结合律**
因为克罗内克乘积是张量积的特殊形式,所以它满足双线性与结合律。
即
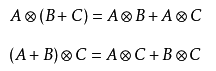
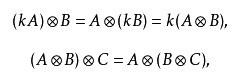
_A $\bigotimes$ B_ 和 _B $\bigotimes$ A_ 是置换等价的,也就是说,存在置换矩阵P和Q,可以使得
_A $\bigotimes$ B=P(B $\bigotimes$ A)Q_
**2.混合乘积性质**
如果存在A,B,C,D这四个矩阵,且矩阵乘积AC和BD存在,那么就有:
_(A $\bigotimes$ B)(C $\bigotimes$ D)=AC $\bigotimes$ BD_
这个性质称为“混合乘积性质”,因为它混合了通常的矩阵乘积和克罗内克积。于是可以得到:当且仅当 _A_ 和 _B_ 是可逆的时, _A$\bigotimes$ B_ 是可逆的。
即
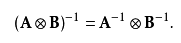
**3.克罗内克和**
如果A是n×n矩阵,B是m×m矩阵,$I_k$表示k×k单位矩阵,那么我们可以定义克罗内克和⊕为:
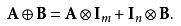
**4.转置**
克罗内克乘积的转置运算符合分配律:
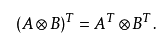
以上便是我的对矩阵的前世今生的研究报告
姓名:张宸宇
学号:B21070428
PS:老师我因为高中写过一篇学习笔记所以就直接拿来用啦,我在原有的基础上补充了一些历史背景与其他。