KMP(MP)小记

今天写了一遍$\text{KMP}$，看来也没有想象中那么难写嘛…… 首先是$\text{next}$数组的求法。很多博客里说是“自匹配求$\text{next}$”，但是我完全不懂。直到看到了知乎上的这篇文章，才终于掌握了求$\text{next}$的方法。这个回答中的“次优”二字很妙，点破了求$\text{next}$的真谛。[如何更好的理解和掌握 KMP 算法? - 逍遥行的回答 - 知乎]( https://www.zhihu.com/question/21923021/answer/37475572) 下面对$\text{next}$数组的求法给予简单说明。 本文中$\text{next[i]}$指的是$\text{s[0...i]}$这一段中，既是**真**前缀又是**真**后缀的最长子串的长度，如在字符串"aaaaa"中，$\text{next[4]}=4$。 我们假设现在已经求出了$\text{next[0]}\sim\text{next[i-1]}$，现在想求$\text{next[i]}$。 我们已知$\text{s[0]}\sim \text{s[next[i-1]-1]}$和$\text{s[i-next[i-1]]}\sim \text{s[i-1]}$这两段是一样的，如果$\text{s[next[i-1]]}$和$\text{s[i]}$也是一样的，那岂不是很好？如果是这样，$\text{next[i]}$便等于$\text{next[i-1]+1}$。 然而有时候~~（大多数时候）~~事情并没有这么简单。我们悲哀地发现$\text{s[next[i-1]]} \neq \text{s[i]}$。这时我们怎么去求$\text{next[i]}$呢？ 我们经过思考可以发现，$\text{s[0]}\sim \text{s[next[i]-2]}$和$\text{s[i-next[i]]}\sim \text{s[i-1]}$这两段是一样的。那么，这两个公共的前缀及后缀应该也是$\text{next[i-1]}$的一个次优解。 我们经过探索知道，$\text{next[i]}$的次优解正是$\text{next[next[i]]}$。 因此，我们的方法是，设一个变量$t$，若$\text{s[i]!=s[t]}$且$t>0$，则使$t$不断等于$\text{next[}t-1\text{]}$。直到跳出循环条件，则把$\text{next[i]}$设为$t+1$或$0$。 求$\text{next[i]}$的代码如下。 ```cpp void get_next(string &s){ int l=s.size(); // l指s的长度 nxt[0]=0; // 0...0没有真前缀/真后缀 for (int i=1;i<l;i++){ //对于[1,l)的每一个字符，计算它的next int t=nxt[i-1]; //t是拟用作next[i]的数据 while (t && s[i]!=s[t]) //如果t不能用作next[i] t=nxt[t-1]; //就寻找下一个可以用作next[i]的t if (s[t]==s[i]) //这里检查结束循环的原因 nxt[i]=t+1; //如果是因为s[i]==s[t]跳出了循环，就说明t+1可以作为next[i] else nxt[i]=0; //如果是因为t==0跳出了循环，说明next[i]只能是0 } } ``` 求$\text{next}$数组这一最艰巨的任务~~（大雾）~~已经完成，下面就是~~比较简单的~~匹配过程了。 我们用$i$指针代表当前扫描到的主字符串的位置，$j$指针代表当前扫描到的模式串的位置。需要注意的有两点，一是出现失配、$j$指针回退时，一定要注意判断$j=0$的边界情况，防止死循环；二是如果恰好出现$i=\text{len}(a),j=\text{len}(b)$的情况，应在循环结束后额外判断。 最后指出一点，洛谷的模板题实质上是$\text{MP}$算法而不是$\text{KMP}$算法，真正的$\text{KMP}$还要对$\text{next}$数组做一些小优化（见[这篇题解](https://www.luogu.org/blog/Bring/solution-p3375)），但是两者在复杂度上没有差别，因此不再深究。 ```cpp #include <iostream> #include <cstdio> #include <string> #define MAXN 1000005 using namespace std; int nxt[MAXN]={0}; void get_next(string &s); int main(void){ string a,b; int i,j; int la,lb; cin >> a >> b; get_next(b); la=a.size(),lb=b.size(); i=j=0; while (i<la){ //Ready to match. if (j==lb){ //Match successfully. cout << i-lb+1 << endl; j=nxt[j-1]; } //Try to match here! if (a[i]==b[j]) i++,j++; else { if (j) j=nxt[j-1]; else i++; } } //Match successfully at the end. if (i==la && j==lb) cout << i-lb+1 << endl; for (int i=0;i<lb;i++) cout << nxt[i] << ' '; cout << endl; return 0; } void get_next(string &s){ int l=s.size(); nxt[0]=0; for (int i=1;i<l;i++){ int t=nxt[i-1]; while (t && s[i]!=s[t]) t=nxt[t-1]; if (s[t]==s[i]) nxt[i]=t+1; else nxt[i]=0; } } ``` --- 等一下，这篇文章还没完！如果$\text{KMP}$只能用于字符串匹配，那我还学它干什么！（大雾）$\text{KMP}$还有一个重要的应用：求解与~~恋爱~~循环有关的问题。 假设我们想要求一个字符串的最小循环节，如"abcabcabcabc"的最小循环节是"abc"，"aaaaaaaa"的最小循环节是"a"，朴素的方法应该是进行$\text{O}(n^{2})$的枚举，但是有了$\text{KMP}$（的$\text{next}$数组），$\text{O}(n)$就可以解决问题！ 来看一个定理。 定理 $22.33$ 恋爱循环定理 设一个字符串$\text{s}[0...n-1]$的长度为$n$，如果$\text{next}[n-1]\neq 0$，且$(n-\text{next}[n-1])\mid n$，即$n\equiv 0\pmod{n-\text{next}[n-1]}$，那么这个字符串是**真**循环的（即循环次数大于$1$），且最小循环节的长度是$n-\text{next}[n-1]$，循环次数是$\frac{n}{n-\text{next}[n-1]}$。 逆命题亦成立，即若一个真循环的字符串$\text{s}[0...n-1]$的最小循环节长度为$t$，则$\text{next}[n-1]=n-t$，且有$t\mid n$。 证明： 不妨设$l=\text{next[}n-1\text{]}$，设$t=n-l$，设$n=kt(k\in \mathbb{N})$。 由于$l\neq 0$，又由$\text{next}$数组中元素的非负性（即$l\ge 0$），知$t < n$。 我们又有$t\mid n$，由整除的性质，我们可以得到$n\ge 2t$，即$k\ge 2$。 由于$l=n-t=kt-t=(k-1)t$，我们知道$t\mid l$。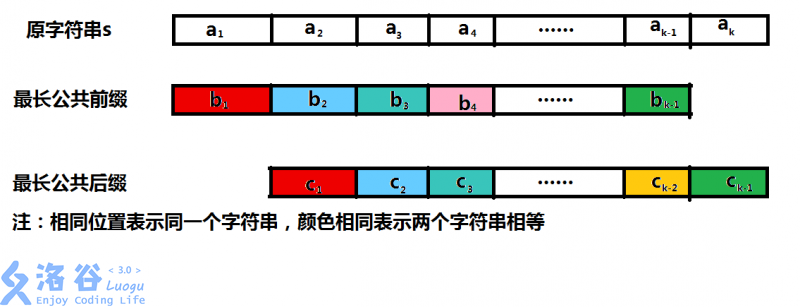 由于$t$是$l$和$n$的公因数，我们可以把$\text{s}[0...n-1]$均分成$k$节，每一节的长度都是$t$；也可以把$\text{s}[0...l-1]$（最长公共前缀）和$\text{s}[n-l...n-1]$（最长公共后缀）均分成$k-1$节，每一节的长度也都是$t$。 下面我们把$\text{s}[0...n-1]$被均分成的$k$节称作$a_{1},a_{2},\cdots,a_{k}$，把$\text{s}[0...l-1]$被均分成的$k-1$节称作$b_{1},b_{2},\cdots,b_{k-1}$，把$\text{s}[n-l...n-1]$被均分成的$k-1$节称作$c_{1},c_{2},\cdots,c_{k-1}$。 由$\text{next}$数组的定义，我们知道$b_{1}=c_{1},b_{2}=c_{2},\cdots,b_{k-1}=c_{k-1}$。 经过仔细比对下标范围~~（其实不那么仔细也可以）~~，我们又发现$a_{1}$和$b_{1}$是同一个字符串（即它们代表着$\text{s}$字符串中同一个字串，不只是内容相同，位置也完全相同）。 经过归纳得出$a_{i}$和$b_{i}$是同一个字符串，其中$i\in \{i\in \mathbb{N} \mid 1\le i \le k-1\}$。同理，$a_{i+1}$和$c_{i}$是同一个字符串，其中$i\in \{i\in \mathbb{N} \mid 1\le i \le k-1\}$。 由$b_{1}=c_{1}$我们知道$a_{1}=a_{2}$，由$b_{2}=c_{2}$我们知道$a_{2}=a_{3}$，由$b_{k-1}=c_{k-1}$我们知道$a_{k-1}=a_{k}$，因此$a_{1}=a_{2}=\cdots=a_{k}$。即$\text{s}[0...t-1]$是$\text{s}$的一个循环节。 如何证明这是最小循环节呢？我们考察一个循环字符串，设它的最小循环节为"a"，设"a"的长度为$t'$，那么整个循环字符串可以表示为"aaaa...aa"($k$个"a")，则$n=kt'$。容易发现，这个字符串的最长公共前后缀是"aaaa...a"($k-1$个"a")，即$l=(k-1)t'$，此时有$t=n-l=t'$，因此我们按照上面的方法计算出的循环节长度$t$和实际最小循环节长度$t'$是相等的，这就说明我们计算出的$t$正是最小循环节长度。 循环次数显然为$\frac{n}{t}$。 整理可知，原命题和逆命题都已证毕。 下面附一张图以方便理解。  现在我们再来解决一个问题。如果一个字符串现在不是真循环字符串，我们现在可以在它的末尾补上若干个字符以使它成为真循环字符串，那么我们至少要补多少个字符呢？ 这个问题其实也不难。要让它成为真循环字符串，只要让它满足~~恋爱~~循环定理的条件即可，即让$(n-\text{next}[n-1])\mid n$成立。很显然，我们应该努力让$\text{next}[n-1]$尽量增大，因此我们补的字符应该是最大公共前缀以后的字符，例如"abcabcefgabcabc"的最大公共前缀是"abcabc"，那么我们就应该给它补上"efg"。这么补的结果就是，$n$和$l$同时增大相同的数值，于是$t$的值不变。 现在问题就转化成：求一个最小的正整数$x$，使得$t\mid (n+x)$。答案很显然，$x=t-n\%t$。于是我们就知道，至少要补上$t-n\%t$个字符，才能使这个字符串成为真循环字符串。问题解决。 总之，$\text{KMP}$算法能够快速进行字符串的匹配，而且$\text{next}$数组也有许多神奇的功能，因此我们应该很好地掌握$\text{KMP}$（大雾）。 ---- 练习 [$\text{KMP}$模板](https://www.luogu.org/problemnew/show/P3375) [求周期模板题](https://www.luogu.org/problemnew/show/UVA455)（数据范围比较小，但是可以作为练习） [$\text{next}$数组的应用1](https://www.luogu.org/problemnew/show/P2375)（此题使用倍增算法也可以勉强过，这里涉及到一个倍增数组（二维数组）的维数优化技巧。） [$\text{next}$数组的应用2](https://www.luogu.org/problemnew/show/P3435)（此题中的周期和上文所述的周期不同。**记得开$\text{long long}$！**） 上述两个$\text{next}$数组的应用主要是用$\text{next}$数组遍历所有公共前后缀，即可以把$\text{next}$数组的内容理解为一棵“公共前后缀树”。