DLX 详细讲解

DLX 指使用 Dancing Links 优化后的 X 算法，在随机情况下能极快速地解决精确覆盖问题。 upd2: 洛谷博客上本文已经不再维护，若需要可移步 [我的博客](http://leverimmy.top/2020/03/16/%E3%80%90%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0%E3%80%91DLX-%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0) 查看最新版本。 upd: 文末引用已更新。 --- ## 一、问题引入 1. 就在刚才，你的同学终于写完了 [P4205 『NOI2005』智慧珠游戏](https://www.luogu.com.cn/problem/P4205)，并向你展示了他的 500+ 行的代码。  **小时候，你玩智慧珠；长大后，智慧珠玩你**，你准备怎么办？ 2. 就在刚才，你的同学码力全开写完了 [P1784 数独](https://www.luogu.com.cn/problem/P1784)，感觉有了暴力搜索，他能 AK 学生会组织的所有数独比赛。  面对数独，你不愿去打那恼人的暴力，你又准备怎么办？ ## 二、精确覆盖问题 1. 定义： 精确覆盖问题 (Exact Cover Problem) 是指给定许多集合 $S_i (1 \le i \le n)$ 以及一个集合 $X$，求满足以下条件的无序多元组 $(T_1, T_2, \cdots , T_m)$： (1) $\forall i, j \in [1, m],T_i\bigcap T_j = \varnothing (i \neq j)$ (2) $X = \bigcup\limits_{i = 1}^{m}T_i$ (3) $\forall i \in[1, m], T_i \in \{S_1, S_2, \cdots, S_n\}$ 例如，若给出 $$ \begin{aligned} & S_1 = \{5, 9, 17\} \\ & S_2 = \{1, 8, 119\} \\ & S_3 = \{3, 5, 17\} \\ & S_4 = \{1, 8\} \\ & S_5 = \{3, 119\} \\ & S_6 = \{8, 9, 119\} \\ & X = \{1, 3, 5, 8, 9, 17, 119\} \end{aligned} $$ 则 $(S_1, S_4, S_5)$ 为一组合法解。 2. 问题转化 我们将 $\bigcup\limits_{i = 1}^{n}S_i$ 中的所有数离散化，那么可以得到这么一个模型： > 给定一个 01 矩阵，你可以选择一些行，使得最终每列都恰好有一个 1。 举个例子，我们对 (2.1) 中的例子进行建模，可以得到这么一个矩阵： $$ \begin{pmatrix} 0 & 0 & 1 & 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 \end{pmatrix} $$ 其中第 $i$ 行表示着 $S_i$，而这一行的每个数依次表示 $[1 \in S_i],[3 \in S_i],[5 \in S_i],\cdots,[119 \in S_i]$。 3. 第一个不优秀的做法： 我们可以枚举选择哪些行，最后检查这个方案是否合法。 因为每一行都有选或者不选两种状态，所以枚举行的时间复杂度是 $O(2^n)$ 的； 而每次检查都需要 $O(nm)$ 的时间复杂度。所以总的复杂度是 $O(nm\cdot2^n)$。 ```cpp int ok = 0; for(int state = 0; state < 1 << n; ++state) { // 枚举每行是否被选 for(int i = 1; i <= n; ++i) if((1 << i - 1) & state) for(int j = 1; j <= m; ++j) a[i][j] = 1; int flag = 1; for(int j = 1; j <= m; ++j) for(int i = 1, bo = 0; i <= n; ++i) if(a[i][j]) { if(bo) flag = 0; else bo = 1; } if(!flag) continue; else { ok = 1; for(int i = 1; i <= n; ++i) if((1 << i - 1) & state) printf("%d ", i); puts(""); } memset(a, 0, sizeof(a)); } if(!ok) puts("No solution."); ``` 4. 第二个不那么优秀的做法： 考虑到 01 矩阵的特殊性质，我们可以把每一行都看做成一个 $m$ 位二进制数。 因此被转化为了 > 给你 $n$ 个 $m$ 位二进制数，要求选择一些数，使得任意两个数的与都为0，且所有数的或为 $2^m - 1$。 `tmp` 表示的是截至目前的所有被选择了的 $m$ 位二进制数的或。 因为每一行都有选或者不选两种状态，所以枚举行的时间复杂度是 $O(2^n)$ 的； 而每次计算 `tmp` 都需要 $O(n)$ 的时间复杂度。所以总的复杂度是 $O(n\cdot2^n)$。 ```cpp int ok = 0; for(int i = 1; i <= n; ++i) for(int j = m; j >= 1; --j) num[i] = num[i] << 1 | a[i][j]; for(int state = 0; state < 1 << n; ++state) { int tmp = 0; for(int i = 1; i <= n; ++i) if((1 << i - 1) & state) { if(tmp & num[i]) break; tmp |= num[i]; } if(tmp == (1 << m) - 1) { ok = 1; for(int i = 1; i <= n; ++i) if((1 << i - 1) & state) printf("%d ", i); puts(""); } } if(!ok) puts("No solution."); ``` ## 三、X 算法 刚才的暴力实在是太菜了！连 $1 \le n,m \le 200$ 都跑不过…… Donald E. Knuth 提出了一个叫做 X 算法 (Algorithm X) 的东西，其思想与刚才的暴力差不多，但是方便优化。 继续以 (2.1) 中提到的例子为载体，我们得到的是一个这样的 01 矩阵： $$ \begin{pmatrix} 0 & 0 & 1 & 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 \end{pmatrix} $$ 1. 此时第一行有 $3$ 个 $1$，第二行有 $3$ 个 $1$，第三行有 $3$ 个 $1$，第四行有 $2$ 个 $1$，第五行有 $2$ 个 $1$，第六行有 $3$ 个 $1$。选择第一行，将它删除，并将所有 $1$ 所在的列打上标记； $$ \begin{pmatrix} \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 \\ 1 & 0 & \color{Red}0 & 1 & \color{Red}0 & \color{Red}0 & 1 \\ 0 & 1 & \color{Red}1 & 0 & \color{Red}0 & \color{Red}1 & 0 \\ 1 & 0 & \color{Red}0 & 1 & \color{Red}0 & \color{Red}0 & 0 \\ 0 & 1 & \color{Red}0 & 0 & \color{Red}0 & \color{Red}0 & 1 \\ 0 & 0 & \color{Red}0 & 1 & \color{Red}1 & \color{Red}0 & 1 \end{pmatrix} $$ 2. 选择所有被标记的列，将它们删除，并将这些列中含 $1$ 的行打上标记； $$ \begin{pmatrix} \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 \\ 1 & 0 & \color{White}\colorbox{Black}0 & 1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}0 & 1 \\ \color{Red}0 & \color{Red}1 & \color{White}\colorbox{Black}1 & \color{Red}0 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{Red}0 \\ 1 & 0 & \color{White}\colorbox{Black}0 & 1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}0 & 0 \\ 0 & 1 & \color{White}\colorbox{Black}0 & 0 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}0 & 1 \\ \color{Red}0 & \color{Red}0 & \color{White}\colorbox{Black}0 & \color{Red}1 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 & \color{Red}1 \end{pmatrix} $$ 3. 选择所有被标记的行，将它们删除； $$ \begin{pmatrix} \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 \\ 1 & 0 & \color{White}\colorbox{Black}0 & 1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}0 & 1 \\ \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 \\ 1 & 0 & \color{White}\colorbox{Black}0 & 1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}0 & 0 \\ 0 & 1 & \color{White}\colorbox{Black}0 & 0 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}0 & 1 \\ \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 \end{pmatrix} $$ **这表示表示我们选择了一行，且这一行的所有 $1$ 所在的列不能有其他 $1$ 了**。 于是我们得到了这样的一个新的小 01 矩阵： $$ \begin{pmatrix} 1 & 0 & 1 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \end{pmatrix} $$ 4. 此时第一行（原来的第二行）有 $3$ 个 $1$，第二行（原来的第四行）有 $2$ 个 $1$，第三行（原来的第五行）有 $2$ 个 $1$。选择第一行（原来的第二行），将它删除，并将所有 $1$ 所在的列打上标记； $$ \begin{pmatrix} \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}1 \\ \color{Red}1 & 0 & \color{Red}1 & \color{Red}0 \\ \color{Red}0 & 1 & \color{Red}0 & \color{Red}1 \end{pmatrix} $$ 5. 选择所有被标记的列，将它们删除，并将这些列中含 $1$ 的行打上标记； $$ \begin{pmatrix} \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}1 \\ \color{White}\colorbox{Black}1 & \color{Red}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 \\ \color{White}\colorbox{Black}0 & \color{Red}1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 \end{pmatrix} $$ 6. 选择所有被标记的行，将它们删除； $$ \begin{pmatrix} \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}1 \\ \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 \\ \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 \end{pmatrix} $$ 于是我们得到了一个空矩阵。但是上次删除的行 "1 0 1 1" 不是全 $1$ 的，说明选择有误； $$ \begin{pmatrix} \end{pmatrix} $$ 7. 回溯到步骤 $4$，我们考虑选择第二行（原来的第四行），将它删除，并将所有 $1$ 所在的列打上标记； $$ \begin{pmatrix} \color{Red}1 & 0 & \color{Red}1 & 1 \\ \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 \\ \color{Red}0 & 1 & \color{Red}0 & 1 \end{pmatrix} $$ 8. 选择所有被标记的列，将它们删除，并将这些列中含 $1$ 的行打上标记； $$ \begin{pmatrix} \color{White}\colorbox{Black}1 & \color{Red}0 & \color{White}\colorbox{Black}1 & \color{Red}1 \\ \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 \\ \color{White}\colorbox{Black}0 & 1 & \color{White}\colorbox{Black}0 & 1 \end{pmatrix} $$ 9. 选择所有被标记的行，将它们删除； $$ \begin{pmatrix} \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}1 \\ \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 & \color{White}\colorbox{Black}1 & \color{White}\colorbox{Black}0 \\ \color{White}\colorbox{Black}0 & 1 & \color{White}\colorbox{Black}0 & 1 \end{pmatrix} $$ 于是我们得到了这样的一个矩阵： $$ \begin{pmatrix} 1 & 1 \end{pmatrix} $$ 10. 此时第一行（原来的第五行）有 $2$ 个 $1$，将它们全部删除，我们得到了一个空矩阵： $$ \begin{pmatrix} \end{pmatrix} $$ 11. 上一次删除的时候，删除的是全 $1$ 的行，因此成功，算法结束。 答案即为我们删除的三行：$1, 4, 5$。 - **强烈建议自己模拟一遍矩阵删除、还原与回溯的过程后再接着阅读下文。** 我们可以概括出 X 算法的过程： 1. 对于现在的矩阵 $M$，选择并标记一列 $r$，将 $r$ 添加至 $S$ 中； 2. 如果尝试了所有的 $r$ 却无解，则算法结束，输出无解。 3. 标记与 $r$ 相关的行 $r_i$ 和 $c_i$； 4. 删除所有标记的行和列，得到新矩阵 $M'$； 5. 如果 $M'$ 为空，且 $r$ 为全 $1$ 的，则算法结束，输出被删除的行组成的集合 $S$； 如果 $M'$ 为空，且 $r$ 不为全 $1$ 的，则恢复与 $r$ 相关的行 $r_i$ 以及列 $c_i$，跳转至步骤 $1$； 如果 $M'$ 不为空，则跳转至步骤 $1$； 不难看出，X 算法需要大量的 “删除行”、“删除列” 和 “恢复行”、“恢复列” 的操作。 Donald E. Knuth 想到了用双向十字链表来维护这些操作。 而在双向十字链表上不断跳跃的过程被形象地比喻成“跳跃”，因此被用来优化 X 算法的双向十字链表也被称为 “Dancing Links”。 ## 四、Dancing Links 优化的 X 算法 0. 预编译命令 ~~这句话太好用了~~ ```cpp #define IT(i, A, x) for(i = A[x]; i != x; i = A[i]) ``` 1. 定义 既然是双向十字链表，那么一定是有四个指针域的：一个指上方的元素，一个指下方的元素，一个指左边的元素，一个指右边的元素。而每个元素 $i$ 在整个双向十字链表系中都对应着一个格子，因此还要表示 $i$ 所在的列和所在的行。像这样：  是不是非常简单？ 而其实大型双向链表其实是长这样的：  每一行都有一个行首指示，每一列都有一个列指示。 行首指示为 `first[]`，列指示是我们虚拟出的 $c + 1$ 个结点。 同时，每一列都有一个 `siz[]` 表示这一列的元素个数。 特殊地，$0$ 号结点无右结点等价于这个 Dancing Links 为空。 ```cpp static const int MAXSIZE = 1e5 + 10; int n, m, idx, first[MAXSIZE + 10], siz[MAXSIZE + 10]; int L[MAXSIZE + 10], R[MAXSIZE + 10], U[MAXSIZE + 10], D[MAXSIZE + 10]; int col[MAXSIZE + 10], row[MAXSIZE + 10]; ``` 2. $\text{remove(c)}$ 操作 $\text{remove(c)}$ 表示在 Dancing Links 中删除第 $c$ 列以及与其相关的行和列。 我们先将 $c$ 删除，此时： (1) $c$ 左侧的结点的右结点应为 $c$ 的右结点； (2) $c$ 右侧的结点的左结点应为 $c$ 的左结点。 即 `L[R[c]] = L[c], R[L[c]] = R[c];`。 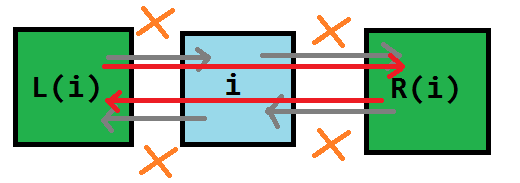 然后我们要顺着这一列往下走，把走过的每一行都删掉。 如何删掉每一行呢？枚举当前行的指针 $j$，此时： (1) $j$ 上方的结点的下结点应为 $j$ 的下结点； (2) $j$ 下方的结点的上结点应为 $j$ 的上结点。 注意要修改每一列的元素个数。 即 `U[D[j]] = U[j], D[U[j]] = D[j], --siz[col[j]];`。  因此 $\text{remove(c)}$ 的代码实现就非常简单了： 其中第一个 `IT(i, D, c)` 等价于 `for(i = D[c]; i != c; i = D[i])`，即在顺着这一列从上往下遍历； 第二个 `IT(j, R, i)` 等价于 `for(j = R[i]; j != i; j = R[j])`，即在顺着这一行从左往右遍历。 ```cpp void remove(const int &c) { int i, j; L[R[c]] = L[c], R[L[c]] = R[c]; IT(i, D, c) IT(j, R, i) U[D[j]] = U[j], D[U[j]] = D[j], --siz[col[j]]; } ``` 3. $\text{recover(c)}$ 操作 $\text{recover(c)}$ 表示在 Dancing Links 中还原第 $c$ 列以及与其相关的行和列。 $\text{recover(c)}$ 即 $\text{remove(c)}$ 的逆操作，在这里就不多赘述了。 **值得注意的是，** $\text{recover(c)}$ **的所有操作的顺序与** $\text{remove(c)}$ **的操作恰好相反。** 在这里给出 $\text{recover(c)}$ 的代码实现： ```cpp void recover(const int &c) { int i, j; IT(i, U, c) IT(j, L, i) U[D[j]] = D[U[j]] = j, ++siz[col[j]]; L[R[c]] = R[L[c]] = c; } ``` 4. $\text{build(r, c)}$ 操作 $\text{build(r, c)}$ 表示新建一个大小为 $r \times c$，即有 $r$ 行，$c$ 列的 Dancing Links。 我们新建 $c + 1$ 个结点，为列指示。 第 $i$ 个点的左结点为 $i - 1$，右结点为 $i + 1$，上结点为 $i$，下结点为 $i$。 特殊地， $0$ 结点的左结点为 $c$，$c$ 结点的右结点为 $0$。 于是我们得到了一条链：  ```cpp void build(const int &r, const int &c) { n = r, m = c; for(int i = 0; i <= c; ++i) { L[i] = i - 1, R[i] = i + 1; U[i] = D[i] = i; } L[0] = c, R[c] = 0, idx = c; memset(first, 0, sizeof(first)); memset(siz, 0, sizeof(siz)); } ``` 这样就初始化了一个 Dancing Links。 5. $\text{insert(r, c)}$ 操作 $\text{insert(r, c)}$ 表示在第 $r$ 行，第 $c$ 列插入一个结点。 我们分两种情况来操作： (1) 如果第 $r$ 行没有元素，那么直接插入一个元素，并使 $first(r)$ 指向这个元素； (2) 如果第 $r$ 行有元素，那么将这个新元素 **用一种奇异的方式** 与 $c$ 和 $first(r)$ 连接起来。 对于 (1)，我们可以通过 `first[r] = L[idx] = R[idx] = idx;` 来实现； 对于 (2)，（我们称这个新元素为 $idx$）： - 我们把 $idx$ 插入到 $c$ 的正下方，此时： (1) $idx$ 下方的结点为原来 $c$ 的下结点； (2) $idx$ 下方的结点（即原来 $c$ 的下结点）的上结点为 $idx$; (3) $idx$ 的上结点为 $c$； (4) $c$ 的下结点为 $idx$。 注意记录 $idx$ 的所在列和所在行，以及更新这一列的元素个数。 ```cpp col[++idx] = c, row[idx] = r, ++siz[c]; U[idx] = c, D[idx] = D[c], U[D[c]] = idx, D[c] = idx; ``` **强烈建议读者完全掌握这几步的顺序后再继续阅读本文。** - 我们把 $idx$ 插入到 $first(r)$ 的正右方，此时： (1) $idx$ 右侧的结点为原来 $first(r)$ 的右结点； (2) 原来 $first(r)$ 右侧的结点的左结点为 $idx$； (3) $idx$ 的左结点为 $first(r)$； (4) $first(r)$ 的右结点为 $idx$。 ```cpp L[idx] = first[r], R[idx] = R[first[r]]; R[first[r]] = idx, L[R[first[r]]] = idx; ``` **强烈建议读者完全掌握这几步的顺序后再继续阅读本文。** 对于 $\text{insert(r, c)}$ 这个操作，我们可以画图来辅助理解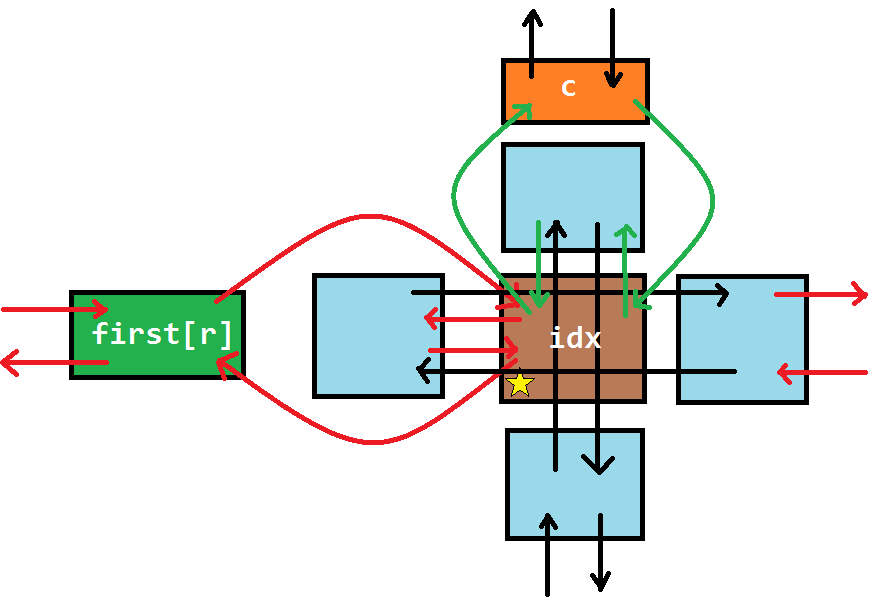：  留心曲线箭头的方向。 在这里给出 $\text{insert(r, c)}$ 的代码： ```cpp void insert(const int &r, const int &c) { row[++idx] = r, col[idx] = c, ++siz[c]; U[idx] = D[idx] = c, U[D[c]] = idx, D[c] = idx; if(!first[r]) first[r] = L[idx] = R[idx] = idx; else { L[idx] = first[r], R[idx] = R[first[r]]; L[R[first[r]]] = idx, R[first[r]] = idx; } } ``` 6. $\text{dance()}$ 操作 $\text{dance()}$ 即为递归地删除以及还原各个行列的过程。 (1) 如果 $0$ 号结点没有右结点，那么矩阵为空，记录答案并返回； (2) 选择列元素个数最少的一列，并删掉这一列； (3) 遍历这一列所有有 $1$ 的行，枚举它是否被选择； (4) 递归调用 $\text{dance()}$，如果可行，则返回；如果不可行，则恢复被选择的行； (5) 如果无解，则返回； 在这里给出 $\text{dance()}$ 的代码实现： ```cpp bool dance(int dep) { int i, j, c = R[0]; if(!R[0]) { ans = dep; return 1; } IT(i, R, 0) if(siz[i] < siz[c]) c = i; remove(c); IT(i, D, c) { stk[dep] = row[i]; IT(j, R, i) remove(col[j]); if(dance(dep + 1)) return 1; IT(j, L, i) recover(col[j]); } recover(c); return 0; } ``` 其中 `stk[]` 用来记录答案。 注意我们每次优先选择列元素个数最少的一列进行删除，这样能保证程序具有一定的启发性（乱扯的），是搜索树分支最少（不会证）。 7. [P4929 【模板】舞蹈链（DLX）](https://www.luogu.com.cn/problem/P4929) [模板代码](https://paste.ubuntu.com/p/kHMDCPxzfJ/) ## 四又二分之一、时间复杂度分 (luàn) 析 (chě) DLX 的时间复杂度是 **指数级** 的，它递归及回溯的次数与矩阵中 $1$ 的个数有关，与矩阵的 $r, c$ 等参数无关。 因此理论复杂度大概在 $O(c^n)$ 左右，其中 $c$ 为某个非常接近于 $1$ 的常数，$n$ 为矩阵中 $1$ 的个数。 但实际情况下 DLX 表现良好，一般能解决大部分的问题。 ## 五、如何建模 DLX 的难点，~~除了垃圾链表连这连那~~就是建模。 **请确保已经完全掌握 DLX 模板后再继续阅读本文。** 我们每拿到一个题，应该考虑行和列所表示的意义： - 行表示 *决策*，因为每行对应着一个集合，也就对应着选 / 不选； - 列表示 *状态*，因为第 $i$ 列对应着某个条件 $P_i$。 对于某一行而言，由于不同的列的值不尽相同，我们 **由不同的状态，定义了一个决策**。 1. 【洛谷】 P1784 数独 [题目链接](https://www.luogu.com.cn/problem/P1784) 先考虑决策是什么。 在这一题中，每一个决策可以用形如 $(r, c, w)$ 的有序三元组表示。 注意到 “宫” 并不是决策的参数，因为它 **可以被每个确定的 $(r, c)$ 表示**。 因此有 $9 \times 9 \times 9 = 729$ 行。 再考虑状态是什么。 我们思考一下 $(r, c, w)$ 这个决将会造成什么影响。记 $(r, c)$ 所在的宫为 $b$。 (1) 第 $r$ 行用了一个 $w$（用 $9 \times 9 = 81$ 列表示）； (2) 第 $c$ 列用了一个 $w$（用 $9 \times 9 = 81$ 列表示）； (3) 第 $b$ 宫用了一个 $w$（用 $9 \times 9 = 81$ 列表示）； (4) $(r, c)$ 中填入了一个数（用 $9 \times 9 = 81$ 列表示）。 因此有 $81 \times 4 = 324$ 列，共 $729 \times 4 = 2916$ 个 $1$。 至此，我们成功地将 $9 \times 9$ 的数独问题转化成了一个**有 $729$ 行，$324$ 列，共 $2916$ 个 $1$** 的精确覆盖问题。 2. 【洛谷】 P1074 靶形数独 [题目链接](https://www.luogu.com.cn/problem/P1074) 这一题与 (5.1) 的模型构建 **一模一样**，主要区别在于答案的更新。 这一题可以开一个权值数组，每次找到一组数独的解时， 每个位置上的数乘上对应的权值计入答案即可。 3. 【洛谷】 P4205 『NOI2005』智慧珠游戏 [题目链接](https://www.luogu.com.cn/problem/P4205) ~~终于，我们打到了大 boss。~~ - 定义：题中给我们的智慧珠的形态，称为这个智慧珠的 *标准形态*。 显然，我们可以通过改变两个参数 $d$（表示顺时针旋转 $90^{\circ}$ 的次数）和 $f$（是否水平翻转）来改变这个智慧珠的形态。 仍然，我们先考虑决策是什么。 在这一题中，每一个决策可以用形如 $(v, d, f, i)$ 的有序五元组表示。 表示第 $i$ 个智慧珠的 *标准形态* 的左上角的位置，序号为 $v$，经过了 $d$ 次顺时针转 $90^{\circ}$。 巧合的是，我们可以令 $f = 1$ 时不水平翻转，$f = -1$ 时水平翻转，从而达到简化代码的目的。 因此有 $55 \times 4 \times 2 \times 12 = 5280$ 行。 需要注意的是，因为一些不合法的填充，如 $(1, 0, 1, 4)$， 所以**在实际操作中，空的智慧珠棋盘也只需要建出 $2730$ 行。** 再考虑状态是什么。 这一题的状态比较简单。 我们思考一下，$(v, d, f, i)$ 这个决策会造成什么影响。 (1) 某些格子被占了（用 $55$ 列表示）； (2) 第 $i$ 个智慧珠被用了（用 $12$ 列表示）。 因此有 $55 + 12 = 67$ 列，共 $5280 \times (5 + 1) = 31680$ 个 $1$。 至此，我们成功地将智慧珠游戏转化成了一个**有 $5280$ 行，$67$ 列，共 $31680$ 个 $1$** 的精确覆盖问题。 ## 六、练习 1. SP1110 SUDOKU - Sudoku [题目链接](https://www.luogu.com.cn/problem/SP1110) 2. 『kuangbin带你飞』专题三 Dancing Links [题表链接](https://vjudge.net/contest/65998#overview) ## 七、总结 DLX 能用来解决精确覆盖问题，而适当地建立起模型后能解决一些毒瘤的大模拟。 但这个东西的复杂度我是真的不会证，各位大佬就权当娱乐好了。 ~~DLX 也不是什么联赛或省选知识点。~~ ## 八、参考资料： 1. 英雄哪里出来 的 [《夜深人静写算法（九）- Dancing Links X（跳舞链）》](https://blog.csdn.net/whereisherofrom/article/details/79220897) 2. 万仓一黍 的 [《跳跃的舞者，舞蹈链（Dancing Links）算法——求解精确覆盖问题》](https://www.cnblogs.com/grenet/p/3145800.html) 3. zhangjianjunab 的 [《DLX算法一览》](https://blog.csdn.net/zhangjianjunab/article/details/83688681) 4. 静听风吟。 的 [《搜索：DLX算法》](https://www.cnblogs.com/aininot260/p/9629926.html) 5. 刘汝佳，陈锋 的 [《算法竞赛入门经典：训练指南》](https://item.jd.com/11111050.html)