【总结】SOS DP
Sljeuo
·
·
个人记录
总概
SOS DP(高位前缀和/子集 DP),状压 DP 的一种,主要用来解决子集方案数和贡献的问题。
由于其计算过程本质是将集合按父子集关系进行逐层累计,因而对于需要求解多种“父集”的问题在时间上有很大的优化(可以理解为把计算出的信息充分压榨或者是算出了一个前/后缀和数组……)。
这类题目通常会加一些奇奇怪怪的限制内容(更多是数学上的),所以该算法更多时候搭配其他算法使用,但其自身的内容大同小异。
正题
-
问题
对于一个长度为 2^n 的序列 a,需求解一序列 f,f_{S}=\sum\limits_{i \in S } a_i。
换句话说,就是求解每种集合中所有子集元素之和的总和。每个 a_i 都只有选和不选这两种状态,所以我们用一串长为 n 的二进制串来表示选择的状态,也方便用位运算快速处理。
-
分析
首先,考虑最朴素的暴力。枚举集合的内容和子集直接统计。
//参考代码
for(int mask = 0;mask < (1<<N); ++mask)
for(int i = 0;i < (1<<N); ++i)
if((mask&i) == i)//判断子集
F[mask] += A[i];
时间复杂度显而易见的高——\mathcal O(4^n)。这肯定是不够快的 :( 我们自己模拟一下,发现有很多的时间浪费在找 S 的子集上。
那,有没有方法让 i 始终是 S 的子集呢?
其实是有的,我们用例子讲话。假设集合 S=1101(约定用二进制数表示集合),那么子集 i 有 8 个:1101,1100,1001,1000,0101,0100,0001,0000(倒着来只是为下文做铺垫罢了)。
因此, $S$ 所含子集数量应当为 $2^{c}$(下文我们约定 $c$ 表示 $S$ 中 $1$ 的个数), $1101$ 中子集数为 $2^3=8$ 也就是这么来的。
也就是现在,我们希望 $i$ 在循环中每次 $01$ 变化的只有对应到 $S$ 上有 $1$ 的那几位。
如果我们将 $S$ 中 $0$ 的那几位省略掉,那么 $8$ 个子集 $i$ 会变成: $111,110,101,100,011,010,001,000$。
非常 amazing 啊,不就是二进制下的 $7 \sim 0$ 嘛。
发现这点之后,我们开始考虑如何让 $i$ 在枚举时: $S$ 有 $1$ 的按二进制一个个数; $S$ 上为 $0$ 的 $i$ 上也通通为 $0$ 。
- ### 新算法
神奇的位运算就出现了(接下来的内容建议结合回溯搜索去理解)。
$i=1101$ 时,下一个 $i$ 应为 $1100$ 。
直观来看,减一即可。那 $i=1100$ 呢?
下一个是 $1001$ ,直接减一会得到 $1011$ ,不符合我们的需求——因为有一位必须为 $0$ 的却出现了 $1$ 。
那去掉不就好了嘛,我们把 $1011$ 和 $S$ 做与操作就得到了 $1001$ (比较粗暴,但其实是对的)——也就是我们现在转移 $i$ 用的 $i \leftarrow (i-1) \operatorname{and} S$。
如果在读的你比较疑惑的话,可以多试几个,其实还是正确的(除非算错)。
这是为什么呢?
设想以下二进制下的减一操作:把最低位的 $1$ 变成 $0$,然后更低位全部变为 $1$。
可以联系到回溯算法,我们在浅层改变选择时,深层的选择就要全部重置重来。
现在二进制下的减一操作不就是如此吗?
况且我们每次要转换的 $i$ 又是 $S$ 的子集,所以一减就会把权值最低的 $1$ 给改为 $0$ ,然后重置更低位的选择。
重置时又会出现不能为 $1$ 的变成 $1$ 了,所以做与操作便可以将不合法的 $1$ 去掉。(这里建议手推一轮)
本质上,这就是二进制下的回溯搜索。
```cpp
//参考代码
for (int mask = 0; mask < (1<<n); mask++)
{
F[mask] = A[0];//特殊位置特殊处理
for(int i = mask; i > 0; i = (i-1) & mask)//顺着来也是可以写的,只是没有这个优雅罢了
F[mask] += A[i];
}
```
那这个神奇的的算法复杂度又是多少呢?
书接上文,我们提到“ $S$ 所含子集数量应当为 $S$ 所含子集数量应当为 $2^c$,那 $S$ 从 $ 0 \sim 2^n-1$,得出时间复杂度为 $\mathcal O(\sum\limits_{i=0}^{2^n-1}\ 2^{c})$ 。
不妨进一步推导。
$$\begin{aligned}\sum_{k=0}^{n}\dbinom{n}{k}2^k&=\sum_{k=0}^{n}\dbinom{n}{k}2^k 1^{n-k}\\&=(1+2)^n\\&=3^n\end{aligned}$$
(上文中的 $k$ 表示 $S$ 中 $1$ 的个数,第二步则用到了二项式定理)
现在,我们成功的将底数减少了 $1$(How great!)。
- ### 正解
不要忘了,SOS DP是状压DP的一种。
设 $f_{S}$ 表示集合为 $S$ 时的子集元素之和的总和。
直接求解整个集合很难,考虑先从部分开始,这里加多一维: $f_{S,i}$ 表示集合 $S$ 在后i位(这里假设最低位为第 $0$ 位,最高位为 $(n-1)$ )已确定时的总和。
一开始什么都不确定,就只有 $a$ —— $f_{S,-1}=a_{S}$ 。然后,对于每个 $S$ (可以理解为相对于子集的“父集”),如果第 $i$ 位为 $0$ 时,子集的第 $i$ 位只能为 $0$ ;如果第 $i$ 位为 $1$ 时,子集的第 $i$ 位可以是 $0/1$。
譬如 $n=4$ , $S=1101$ , $i=1$ 时,对应位上的是 $0$ ,所以子集在第 $i$ 位这里只有 $1101$ 。
而 $i=2$ 时,对应位为 $1$ ,这里的子集就有 $1101$ 和 $1001$ 二者。
总而言之表示出来就是
$${S \text{在第} i \text{位的子集}} = \begin{cases}
S & {S \text{第} i \text{位为} 0/1} \\
S \oplus 2^i & {S \text{第} i \text{位为} 1}
\end{cases}$$
累计贡献(状态转移方程)
$$f_{S,i}= \begin{cases}
f_{S,i-1} & {S \text{第} i \text{位为} 0} \\
f_{S,i-1}+f_{S \oplus \text{(1<<i)},i-1} & {S \text{第} i \text{位为} 1}
\end{cases}$$
可以结合下图理解( $S=10110$ ):
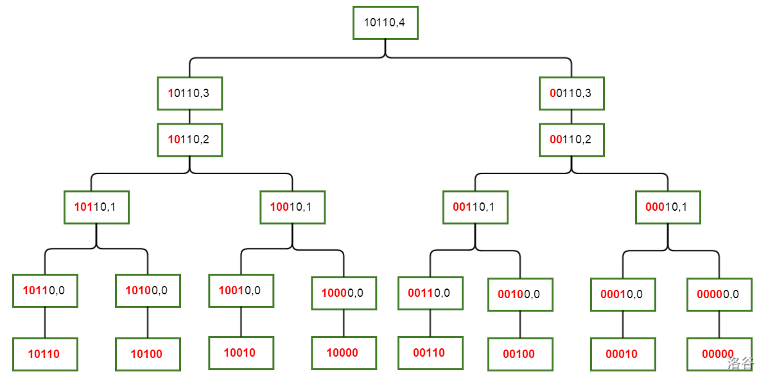
通过方程,我们可以发现 $f_{S,i-1}$ 需要先求解了这里的 $f_{S,i}$ 才能统计。
因此, $i$ 需要从小到大。
参考代码:
```cpp
for(int mask = 0; mask < (1<<N); ++mask)
{
f[mask][-1] = a[mask]; //初始化
for(int i = 0;i < N; ++i)
{
if(mask & (1<<i))
f[mask][i] = f[mask][i-1] + f[mask^(1<<i)][i-1];//mask第i位为1时
else
f[mask][i] = f[mask][i-1];
}
F[mask] = f[mask][N-1];//得出最终结果
}
```
总的下来,这个算法的时间复杂度降低到了 $\mathcal O(n \ast 2^n)$ 。
这个复杂度看似很大,但实际题目中需要给出 $a$ ,因此实际的 $N$ 表示的是上面的 $2^n$ ——时间复杂度表示为 $\mathcal O(Nlog(N))$ 。
- ### 改进
通过方程以及代码,不难看出,对于 $f_{S,i}$ ,只需要用到 $i-1$ 这一列的 $f$ 值——滚动数组也就呼之欲出了:
```cpp
//参考代码
for(int i = 0; i<(1<<N); ++i)
f[i] = a[i];
for(int i = 0;i < N; ++i)
for(int mask = 0; mask < (1<<N); ++mask)
if(mask & (1<<i))
f[mask] += f[mask^(1<<i)];
```
代码大大变短,空间复杂度也降低到了 $\Theta(2^n)$ ,这对于一些对空间卡的很厉害的题目大有帮助。
- ### 新的问题
上述代码将 $f$ 成功降维打击,但有的人可能就会想到使用滚动数组随之带来的一个细节问题——mask的顺序(这个问题其实在学习01背包的时候便有出现)。
但其实这个问题在这里是没有的,无论mask以什么顺序都是可以的(但主要还是要看个人写法)。
原因也很简单,对于第 $i$ 位能够有两个子集的 $f_S$,其 $S\operatorname{and} 2^i$ 的 $i$ 位必然是 $0$ ,即 $f_{S\operatorname{and} 2^i}$ 直接继承 $i-1$ 的值。
这样的话,就说明不会有因顺序原因被覆盖 $f_{i-1}$ 的 $f_i$ 导致其“父集”加上了一些多余的贡献。
至此,SOS DP的模板就到这里了。(其实对 $f$ 进行差分可以求出集合恰好为 $S$ 的贡献(因为 $f$ 其实是一个维度为 $n$ 的前$\text{/}$后缀和),这对一些要求集合恰好的问题很有帮助)
- ### [参考文献](https://codeforces.com/blog/entry/45223)
- ### 致谢
感谢[ZillionX](https://www.luogu.com.cn/user/283913)的指导,这篇文章才会有这样“美轮美奂”的格式:)
- ### P.S
相关题目,参见[这个](https://www.luogu.com.cn/blog/Sljeuo/post-ti-xie-sos-dp-ji-lie-ti-mu)