sigma_bin

· · 个人记录

>>>\sum_{d|n}\phi(d)=n

https://blog.csdn.net/wt_cnyali/article/details/78369210

列出

\frac{1}{n}, \frac{2}{n}, \frac{3}{n}, \cdots,\frac{n}{n}

一共n个分数，再将他们化简． 最简分数\frac{a}{b}在上面出现的话，当且仅当b|n且(a,b)=1。 那么以b为分母的分数共\phi(b)个。 分母一共被划分为\sum_{d|n}1份． 所以

n = \sum_{d|n}\phi(d)

>>> \phi(n)=\sum_{d|n}\mu(d)\frac nd

证明莫比乌斯反演定理

https://blog.csdn.net/outer_form/article/details/50588307

莫比乌斯反演定理形式一：

F(n)=\sum_{d|n}f(d)=>f(n)=\sum_{d|n}\mu(d)F(\frac{n}{d})

证明: 恒等变形得：

f(n)=\sum_{d|n}\mu(d)F(\frac{n}{d})=\sum_{d|n}\mu(d)\sum_{k|\frac{n}{d}}f(k)=\sum_{k|n}f(k)\sum_{d|\frac{n}{k}}\mu(d)

因为之前证明的这个定理：

\sum_{d|n}\mu(d)=\begin{cases}1&n==1\\0&n>1\end{cases}

所以当且仅当\frac{n}{k}=1，即n=k时，\sum_{d|\frac{n}{k}}\mu(d)=1,其余时候等于0。 故

\sum_{k|n}f(k)\sum_{d|\frac{n}{k}}\mu(d)=f(n)

莫比乌斯反演定理形式二：

F(n)=\sum_{n|d}f(d)=>f(n)=\sum_{n|d}\mu(\frac{d}{n})F(d)

证明： 令k=\frac{d}{n},那么，就得到

f(n)=\sum^{+\infty}_{k=1}\mu(k)F(nk)=\sum^{+\infty}_{k=1}\mu(k)\sum_{nk|t}f(t)=\sum_{n|t}f(t)\sum_{k|\frac{t}{n}}\mu(k)

所以当且仅当\frac{t}{n}=1，即t=n时，\sum_{k|\frac{t}{n}}\mu(k)=1,其余时候等于0。 故得到

\sum_{n|t}f(t)\sum_{k|\frac{t}{n}}\mu(k)=f(n)

证明完毕。

原根

1,2,4,p,2p,p^k有原根，原根个数为\phi(\phi(n))

欧拉函数线性筛法

int n=100000,phi[N],np[N],p[N],sz;
phi[1]=1;
for (int i=2;i<=n;++i) {
    if (!np[i]) p[++sz]=i,phi[i]=i-1;
    for (int j=1;j<=sz&&i*p[j]<=n;++j) {
        np[i*p[j]]=1;
        if (i%p[j]) phi[i*p[j]]=phi[i]*(p[j]-1);
        else { phi[i*p[j]]=phi[i]*p[j]; break; }
    }
}

约数个数

约数个数函数。因此，我先给出这个函数的一个重要性质：

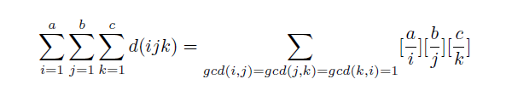
$$ d(ij)=\sum_{x|i}\sum_{y|j}[gcd(x,y)=1]$$ ![约数](http://codeforces.com/predownloaded/e4/e7/e4e790dac57351464a4162c7394bd3431eeeab5d.png) 欧拉函数的延伸: 于或等于n的数中，与n互质的数的总和为：φ(x) * x / 2 (n>1)。 显然有以下常见的卷积形式 任意函数卷积单位元仍为它本身 d=1∗1 σ=id∗1 因为$e(n)=∑d|nμ(d)

所以

e=1∗μ 因为φ(n)=∑d|nμ(d)nd

所以

φ=μ∗id 因为n=∑d|nφ(d)

所以

id=φ∗1

杜教筛

https://www.cnblogs.com/Mychael/p/8744633.html

说了那么多，回归到杜教筛吧： 我们要求的是:

S(n) = \sum_{i=1}^{n} f(i)

我们找到另一个积性数论函数g(n) 那么

\sum_{i=1}^{n}(f*g)(i) = \sum_{i=1}^{n} \sum_{d|i} g(d) * f(\frac{i}{d}) \qquad \qquad = \sum_{i=1}^{n} g(i) * \sum_{j = 1}^{\lfloor \frac{n}{i} \rfloor} f(j) \qquad \qquad = \sum_{i=1}^{n} g(i) * S(\lfloor \frac{n}{i} \rfloor)

我们就有：

\sum_{i=1}^{n}(f*g)(i) = \sum_{i=1}^{n} g(i) * S(\lfloor \frac{n}{i} \rfloor)

就可以有：

g(1) * S(n) = \sum_{i=1}^{n}(f*g)(i) - \sum_{i=2}^{n} g(i) * S(\lfloor \frac{n}{i} \rfloor)

如果我们能找到一个函数g(n) 使得\sum_{i=1}^{n}(f*g)(i)可以被快速计算

莫比乌斯函数:S(n)=1-\sum_{d=2}^nS(\frac nd)

欧拉函数: S(n)=\frac{n(n+1)}2-\sum_{d=2}^nS(\frac{n}d)

https://vjudge.net/problem/51Nod-1244

自然数平方和立方和

扩展欧拉定理

https://www.cnblogs.com/ywwyww/p/8510981.html a^b≡x(mod m) 求x

gcd(a,m)=1，欧拉定理：a^b≡a^(b%φ(m))(mod m)

gcd(a,m)>1，且b>φ(m)，扩展欧拉定理：a^b≡a^(b%φ(m)+φ(m))(mod m)

（b<=φ(m)时，直接用a^b求就可以了）