容斥の说明
Littlestr
·
·
个人记录
(Markdown是真的烦
前置符号:\cup并集,\cap交集,\Sigma求和
先来几个小学教过的公式:
(左边集合设为A,右边集合设为B)
有|A \cup B| = |A|+|B|-|A \cap B|
(下面集合设为C)
有|A \cup B \cup C| = |A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A \cap B \cap C|
这都很好理解,不解释了
然后是n个集合的这种图
有\bigcup\limits_{i = 1}^{n} A_i = \sum\limits_{i = 1}^{n}|A_i|-\sum\limits_{i = 1}^{n}\sum\limits_{j=i+1}^{n}|A_i\cap A_j|+\sum\limits_{i=1}^{n}\sum\limits_{j=i+1}^{n}\sum\limits_{k=j+1}^{n}|A_i\cap A_j\cap A_k|-...+(-1)^{n+1}\bigcap\limits_{i = 1}^{n}A_i
(手麻了
例1
求正整数N以内被3、5、7的数的个数
要求的就是:
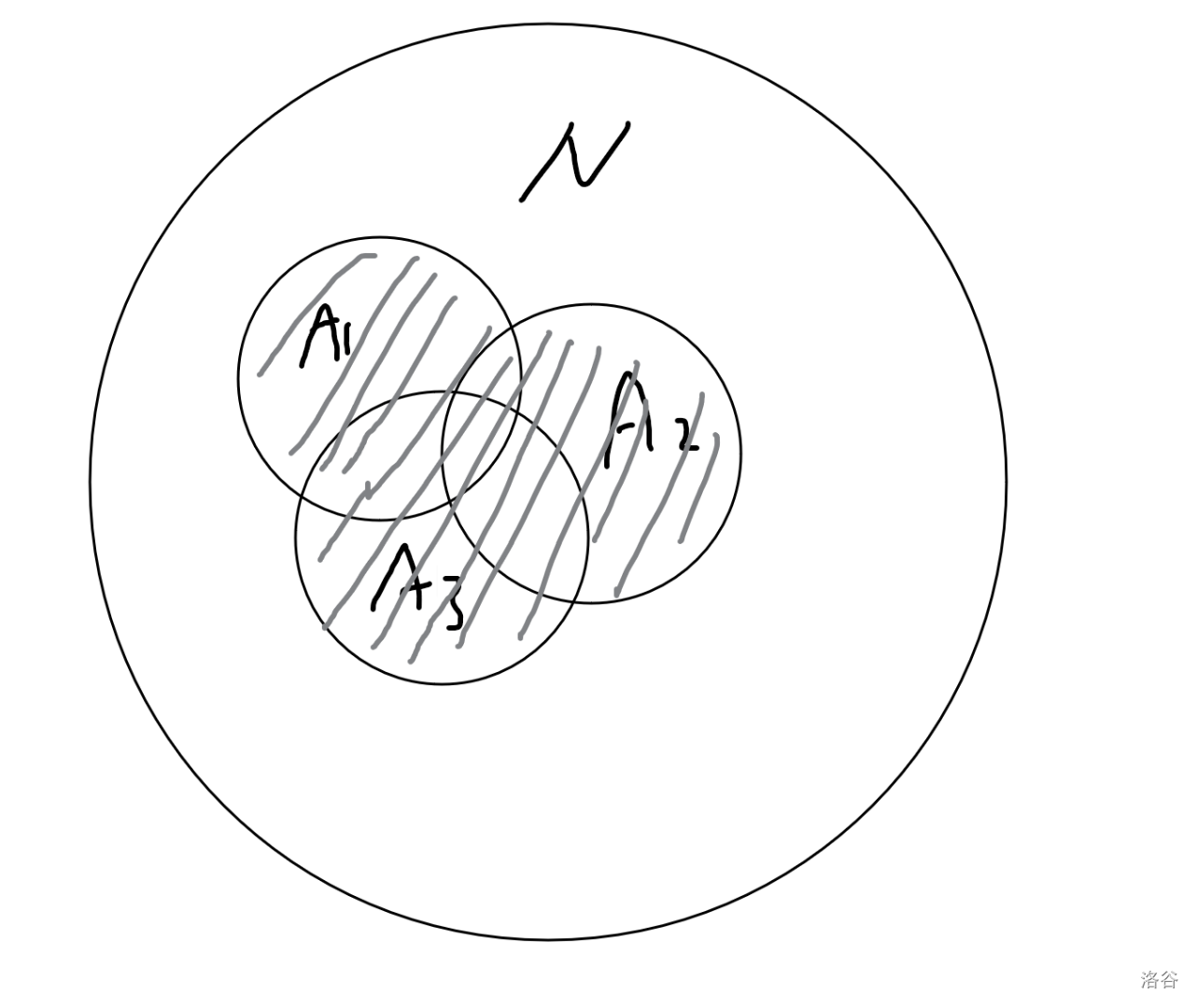
阴影部分↑↑↑
标准点说,就是$A_1$、$A_2$、$A_3$的**并集**
即$|A_1\cup A_2\cup A_3|
= \sum\limits_{i=1}^{3} |A_i| -\sum\limits_{i=1}^{3}\sum\limits_{j=i+1}^{3}|A_i\cap A_j| + |A_1 \cap A_2 \cap A_3|
聪明的狗一定知道三个集合的数字个数吧,答案就呼之欲出了
例2
第一题就不说了,第二题也没区别
第三题:
要求的也是阴影面积
= |A_1| - \sum\limits_{i=2}^{3} |A_1 \cap A_i| + |A_1 \cap A_2 \cap A_3|
第四题:转化一下问题,把N以内的与300互质的数,转化为N以内与300有公因数,最后减一下
附:300的质因数有2、3、5
= N-|A_1\cup A_2\cup A_3|
= N-(\sum\limits_{i=1}^{3} |A_i|-\sum\limits_{i=1}^{3}\sum\limits_{j=i+1}^{3}|A_i \cap A_j|+|A_1 \cap A_2 \cap A_3|)
错位排列
定义:长度为N的一组排列,满足下标与元素不同 (好中二的名字
在长度的N = 3时,有这么三个集合,每个集合定义为当前元素与下标相等的排列数
那就十分简单了:
= P_{3}^{3}-|A_1\cup A_2 \cup A_3|
推导到N在正整数范围时
= P_{n}^{n}-\bigcup\limits_{i=1}^{n}|A_i|
实际上P_{n}^{n} = n!即所有排列的数量(全排列)
然后算后面的并集
根据上面的公式,
\bigcup\limits_{i=1}^{n}|A_i|
= \sum\limits_{i=1}^{n}|A_i|-\sum\limits_{i=1}^{n}\sum\limits_{j=i+1}^{n}|A_i \cap A_j| ... +(-1)^{n+1}\bigcap\limits_{i=1}^{n}|A_i|
用组合数的思想就是,有一个数固定在某个下标上,其他的数自由排列
因为有$n$个数,所以后面的是全排列
所以也挺简单的出来了:$C_{n}^{1}P_{n-1}^{n-1} = n!
同理 ,再举一个例子,书上的我就不举了,这是三个数的交集
\sum\limits_{i=1}^{n}\sum\limits_{j=i+1}^{n}\sum\limits_{k=j+1}^{n}|A_i \cap A_j \cap A_k|
这表示的是有三个数在相应的下标上,剩下的自由排列
不多赘述: = C_{n}^{3}P_{n-3}^{n-3}
展开= {n!}\over{6}
把这个公式推导到n个数中k个数的交集
= C_{n}^{k}P{n-k}^{n-k}
= $ ${n!}\over{k!\times (n-k)!}$ $\times$ $(n-k)!
= $ ${n!}\over{k!}
再用这个公式推导出所有的数:
= P_{n}^{n}-\sum\limits_{i=1}^{n}(-1)^{i}(i!)^{-1}
下面的大佬递推公式我也不知道怎么弄·-·
《保姆级养狗教学》