初中数学中的最值问题
xieyuhao2022
·
·
个人记录
问题背景
进入初中以来,我们已经学习过不少有关最值的数学问题。
而这类问题往往变幻无穷,特别是涉及多种几何图形的变化,以至于我们在面对此类最值类问题时无从下手。
本文旨在帮助读者认识各类常见的初中最短距离问题模型,理解最值问题的本质,并归纳出对应思路。同时,本文会对最值问题在生活中的应用加以一定的介绍。
本文将结合结合初中数学书与生活实际进行创作。
模型归纳
最值基础
我们将几何图形放到坐标系中。
当动点的运动轨迹是一条直线时,显然需要利用垂线段最短。
当动点在圆弧上运动时,我们可以直接连接定点与圆心,动点何时与此线段距离最短,何时拥有最小值。
最值是最能考验数学思维的问题,在研究前,我们应当已经清楚各种基础几何图形的知识。
轴对称
轴对称的概念我们曾在八年级上册的数学学习中了解,它也是解决最值问题的重要工具。
1.将军饮马
我们所熟知的将军饮马便是轴对称应用的最好例子。
将军饮马原文讲述一位将军,从军营出发,先到一条河边饮马,再骑马至练兵场,求其最短路径。
我们将条件抽象为几何图形,如下图所示。当两地分居河流两岸时,根据两点之间,线段最短这一公理,我们不难得出饮马点即为两地连线与河流交点。
同理,当两地在河流同侧,我们将其中一点对称,便得到上述模型。
轴对称的应用远不止于此。
2.“一定两动”与“多定两动”
如下图,有两线段 l_1,l_2 交于点 O,点 P 在两线段围成的夹角内部。在夹角的两边上分别寻找两点 M,N 使得 C_{\Delta PMN} 最小。
将 P 分别对夹角两边做轴对称,本身并无关联的三条线段此时连为一体。
易知,三点共线时有最小值。
当我们将角内部的点增加,做法大同小异,读者可以自行观察图形得出结论。
这一类最值问题也常在生活中见到。角的两边可以看作是两条街道,在街道夹角内部中的街区需要建立起多个居民楼,而在两条街道上均需要建立一些生活超市。为居民出行方便,要求行走路线最短。
我们便可将其代入,画出对应图形求解。
**3.垂线段+轴对称**
已知 $P$ 为 $\angle{O}$ 外的一点,在 $\angle{O}$ 的两边上分别寻找两点 $M,N$ 使得 $PM+MN$ 最小。
自然想到过 $P$ 作较远边的垂线,两交点即为 $M,N$。
当 $P$ 在内部时如何,相信各位读者都已经有了思路。将 $P$ 对称到角外侧,做法同上。
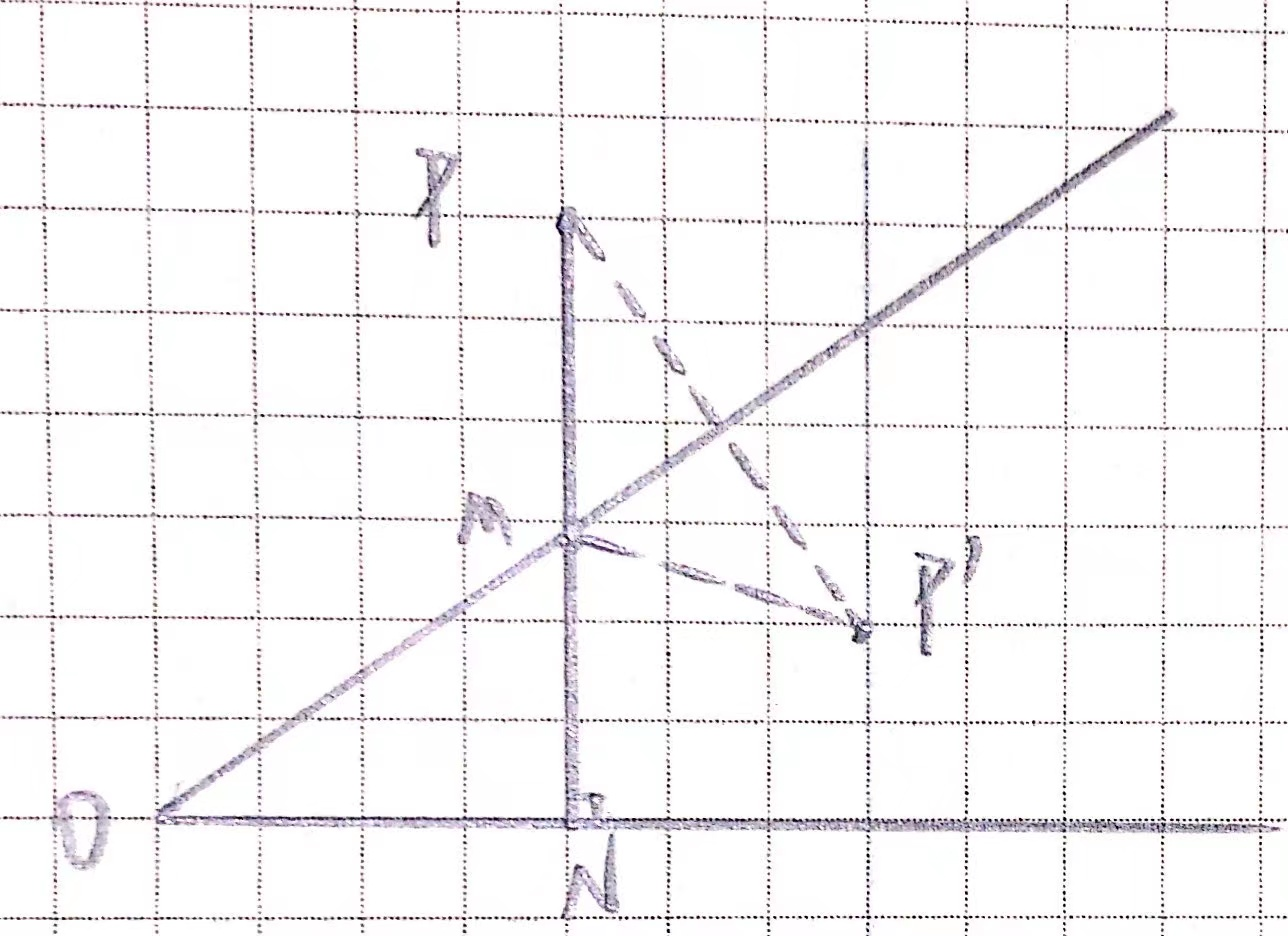
**4.多个动点**
当我在研究轴对称时,不禁想到多个动点的问题该如何解决。
问题如下:在 $\Delta ABC$ 中,点 $P,M,N$ 分别是三角形三边上的动点,求 $C_{\Delta PMN}=PM+PN+MN$ 的最小值。
利用“一定两动”的知识,我们不难想到可以将点 $P$ 进行轴对称,从而得出 $P_1P_2$ (参见上文) 的值。
但是 $P$ 是一个动点,$P_1$ 和 $P_2$ 是会随 $P$ 而变的,我们似乎没了头绪。
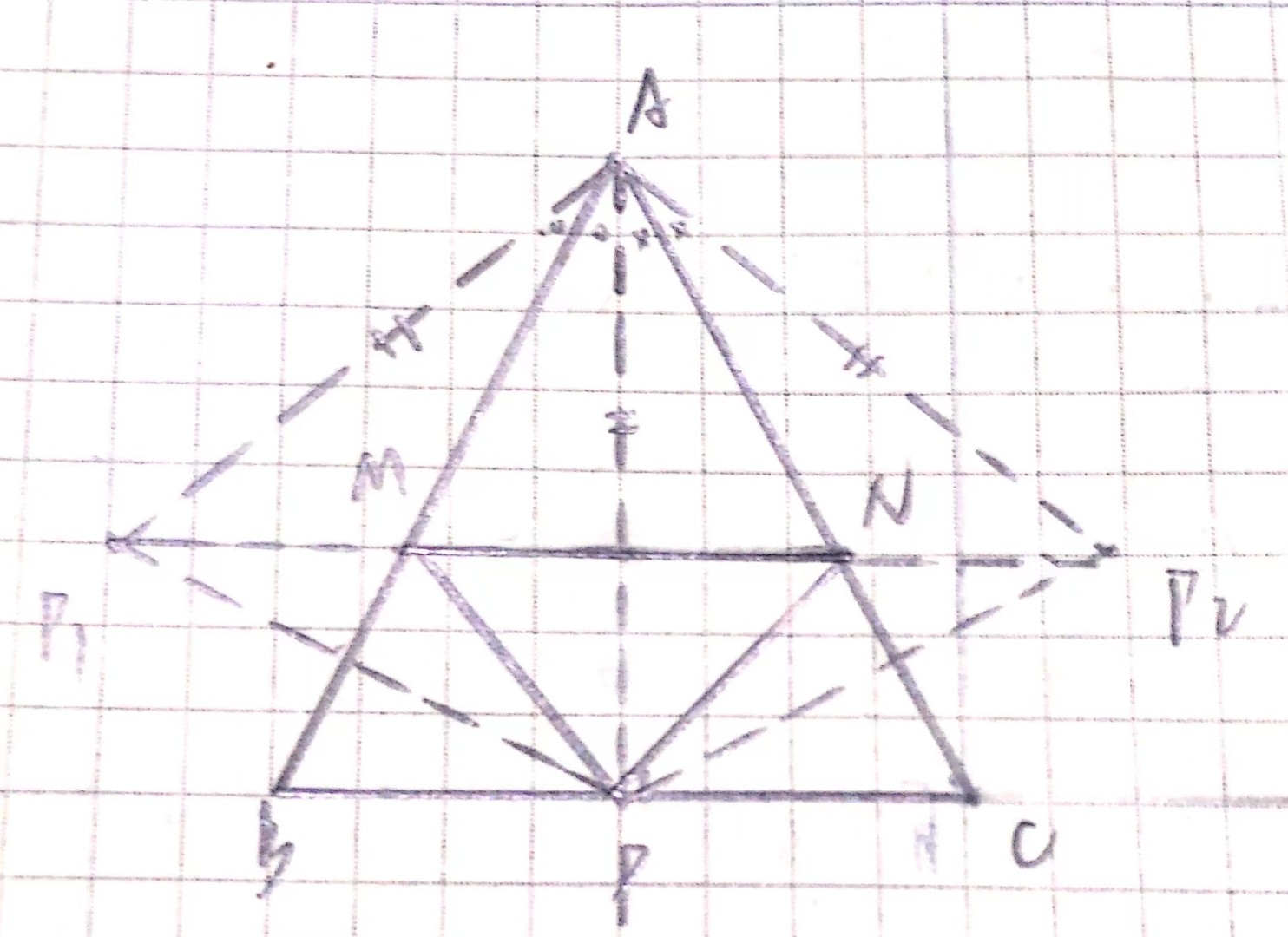
观察图像,根据轴对称的性质,$AP_1=AP_2=AP$,因此,$\Delta AP_1P_2$ 是一个等腰三角形,且其顶角一定。那么,也就是说,当腰越短时,其底边就越短。
当 $AP\bot BC$ 时取得最小值,问题解决。
### 三角形与四边形
几何中的最值问题常出现在三角形与四边形中,运用此二工具可以帮助我们快速解决问题。
**1.中位线与斜边中线**
在有中点的图形中,常用到这两个工具,辅助进行线段范围的求解。
斜边中线也常与圆的思想联系在一起。
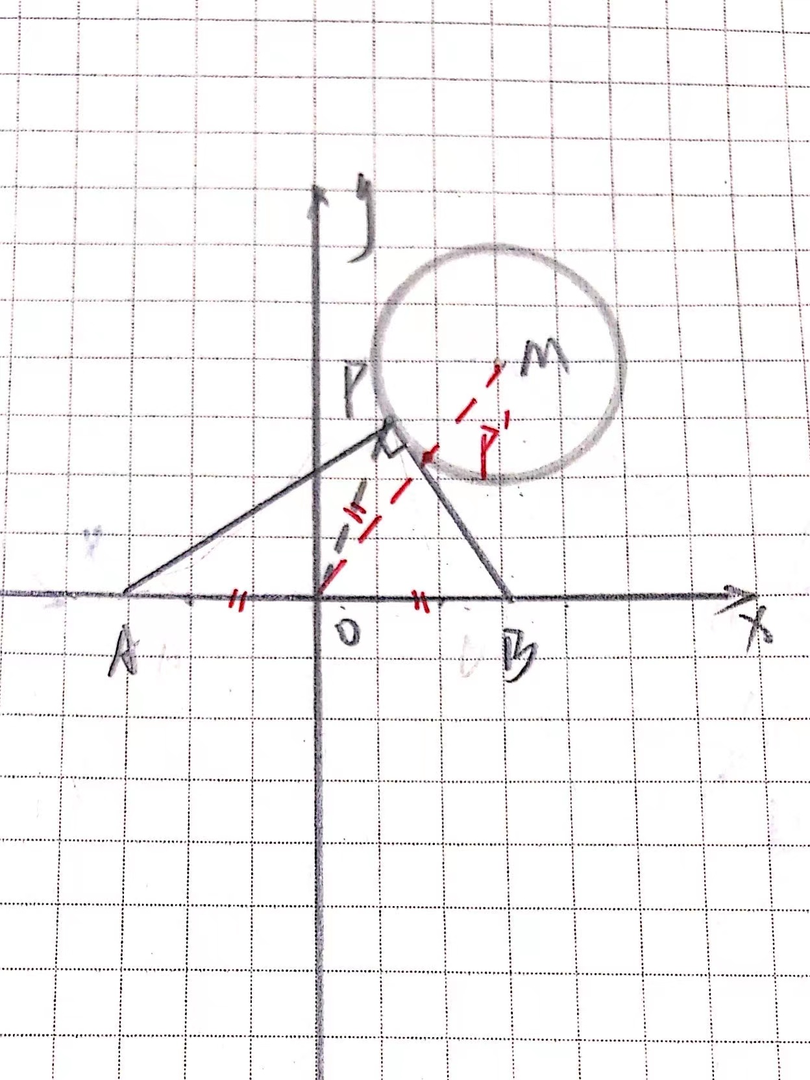
如上图,$M(3,4)$,$\odot M$ 是以 $M$ 为圆心半径为 $2$ 的圆,$A,B$ 均在 $x$ 轴上且 $A,B$ 关于点 $O$ 对称,$P$ 在 $\odot M$ 上运动且 $AP\bot BP$,求 $AB$ 最小值。
其实提示已经十分明显,$P$ 是直角顶点,而 $O$ 即为 $AB$ 中点。连结 $OP$ 可以得到 $OP=OA=OB$,那么当 $OP$ 最小时有答案,问题解决。
**2.平行四边形**
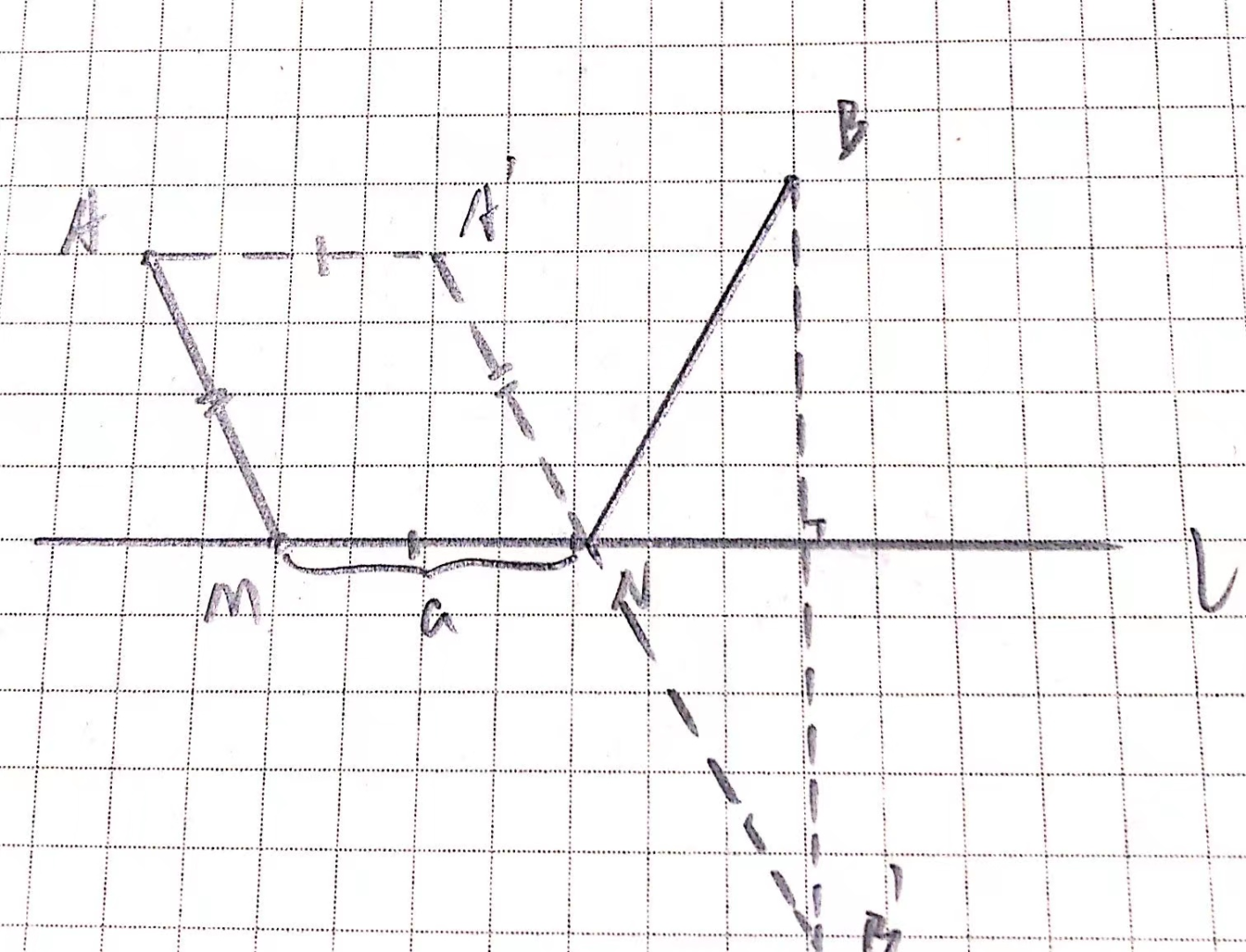
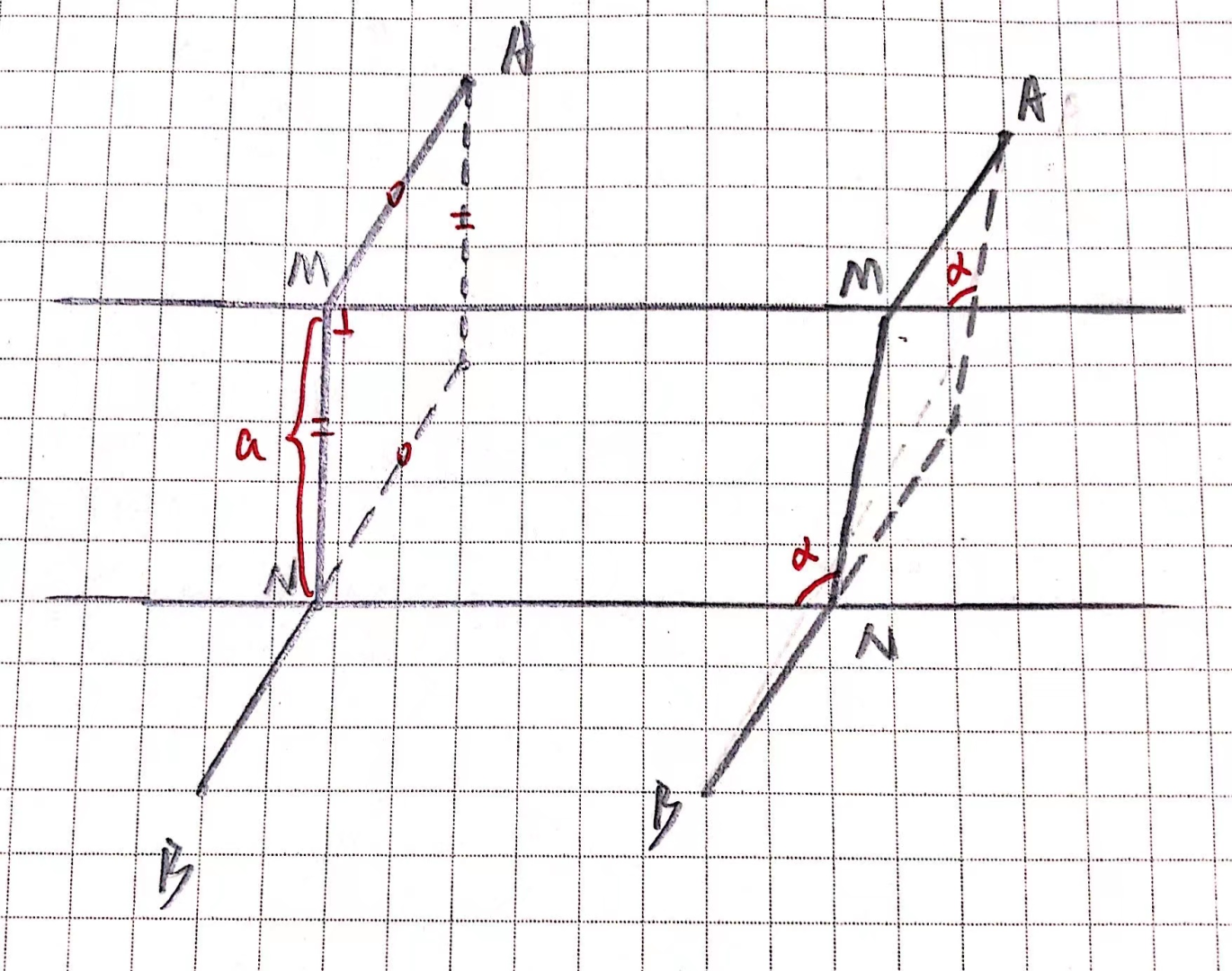
我们有将军饮马的第二个故事。
当将军饮马后,想在河边观察一下对岸形式,他一路走了 $a$ 个单位长度,随后再直线返回军营,求最短路径。
其实,我们可以作一个平行四边形,路径不变的前提下,我们便将其转换为基础的将军饮马了,具体见下图。
当我们将这个思想放到生活中,另一个问题诞生了。现在要建设一条从 $A$ 地到 $B$ 地的小路,其中经过一条河,求最短路径。
不妨将直线拓宽成两条,作为河的两岸。再次利用平行四边形,从起始点先行走完一条桥的长度,再进行连结,求出一案的交点,对岸也就迎刃而解。
如果桥是斜的,我们便量取角度,做出相似图形,这便是过桥问题。
**3.三角形与旋转**
前置知识:三角形两边之和大于第三边,三角形两边之差小于第三边。
通过旋转,我们可以集中条件,帮助我们解决问题。
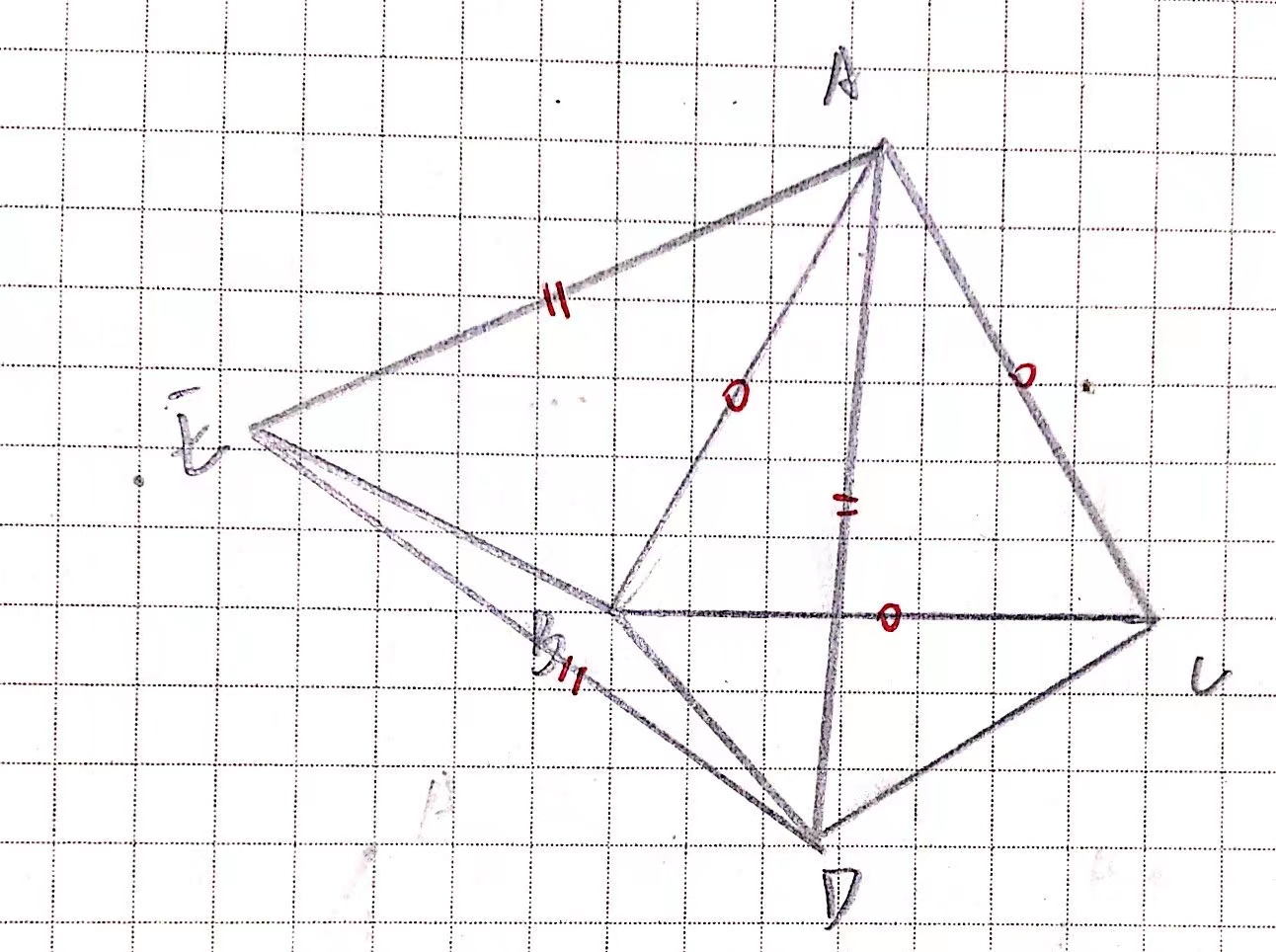
以下是一个常见的例子。在等边 $\Delta ABC$ 下方有一点 $D$,$BD=4,DC=5$,求 $AD$ 的最大值。
第一眼,似乎没有什么思路,虽然已知大多边的长度,但 $D$ 的轨迹或位置却无法确定。此时,我们就需要旋转帮我我们解决问题。
已知等边三角形,那么随其思路,将 $\Delta ADC$ 绕 $A$ 顺时针旋转 $60^{\circ }$ 得到 $\Delta AEB$,连结 $DE$。
不难发现,我们已经创造出了一个新的等边,$AD=DE=AE$,而在下方,有 $\Delta EBD$,满足 $DE\leq BE+BD$,即 $AD\leq BD+CD$,$AD_{max}=9$。
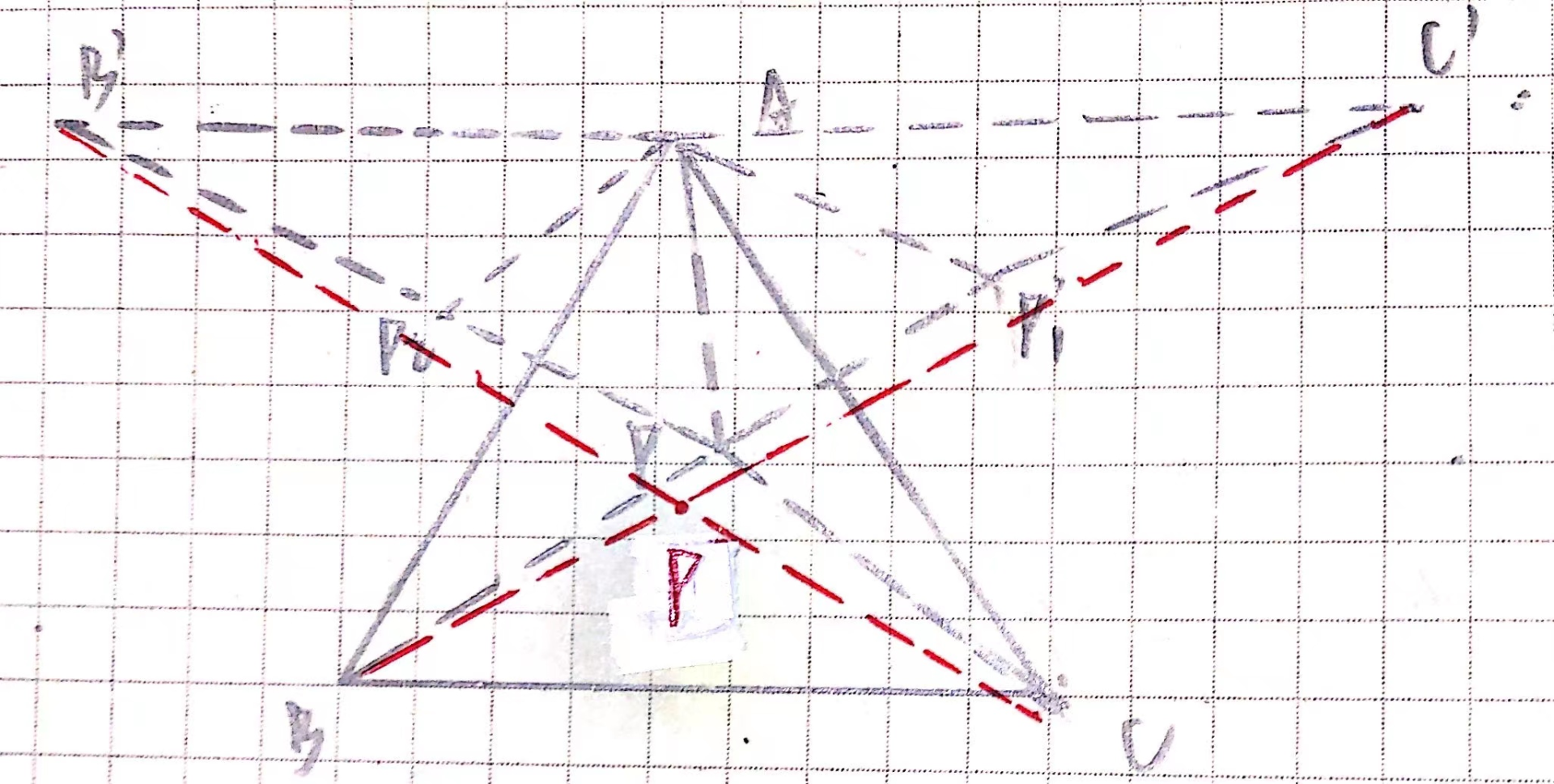
费马点问题是旋转中的一类经典问题。
它的问题是:在 $\Delta ABC$ 寻找一点 $P$ 使得 $PA+PB+PC$ 最小。
这个问题有许多解法,但旋转法仍是最简单快捷的方法。
随意在三角形中取一点 $P$,将 $\Delta APC,\Delta APB$分别向外旋转 $60^{\circ}$ 得到
以 $\Delta APC$ 为例,此时 $PA+PB+PC=PP_1+PB+P_1C'\geq BC'
当三点共线时,明显有最小值。
**4.总结**
三角形与四边形的最值问题可以说千变万化,无所不有;本文仅仅列举了几个常见或具有代表性的模型予以讲解。
包括等腰三角形、菱形、矩形与正方形等,也是具有研究意义的最值图形。
本文篇幅有限,加之做作者重在讲解思路,内容方面不会涉猎过广。
### 胡不归与阿氏圆
**1.胡不归问题**
本质是一类 $PA+m\cdot PB$ 的问题,其中,$A,B$ 为定点,$P$ 为动点。
常见的胡不归模型如下图所示,我们将利用图中所标出的 $\alpha$ 与 $m$ 进行讲解。
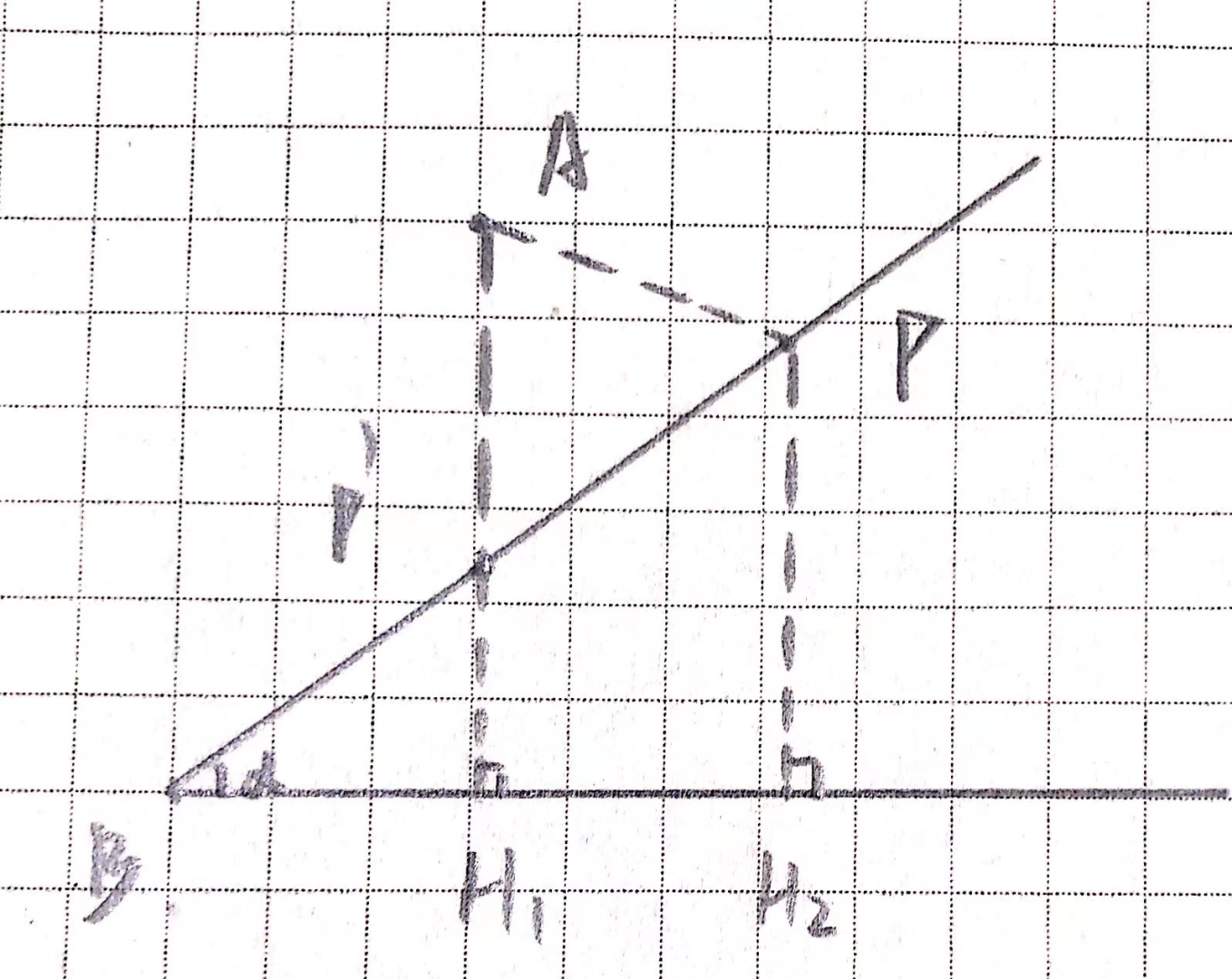
一般而言,此类最值问题仍然是应用在街区设计、区域发展、交通等方面。
我们以 $\alpha=30^{\circ},m=\dfrac{1}{2}$ 为例。
此时,$PA+\dfrac{1}{2}PB=PA+PH_2\geq AH_1(AH_1\bot BH_2)$,我们便将动线转换为了定长。
若 $\alpha$ 为其它度数时,我们便可以相应的构造出对应长度的垂线。反之同理,当我们知道 $m$ 时,我们便要尝试构造出含有对应长度的角度(也可以称构造对应的三角形)。
胡不归问题及其考验思维能力,一定要找准对应点,构造对应方向。
**2.阿氏圆问题**
阿氏圆问题与胡不归问题的题面十分相似,但 $P$ 在圆上运动。
**阿波罗尼斯圆定理**:到两定点 $A,B$ 距离之比为 $\dfrac{m}{n}\neq 1$ 的点 $P$ 位于把线段 $AB$ 分成 $\dfrac{m}{n}$ 的内分点 $C$ 和外分点 $D$ 为直径两端的定圆周上。
**角平分线定理**: 三角形一个角的平分线,这个角平分线其对边所成的两条线段与这个角的两邻边对应成比例。
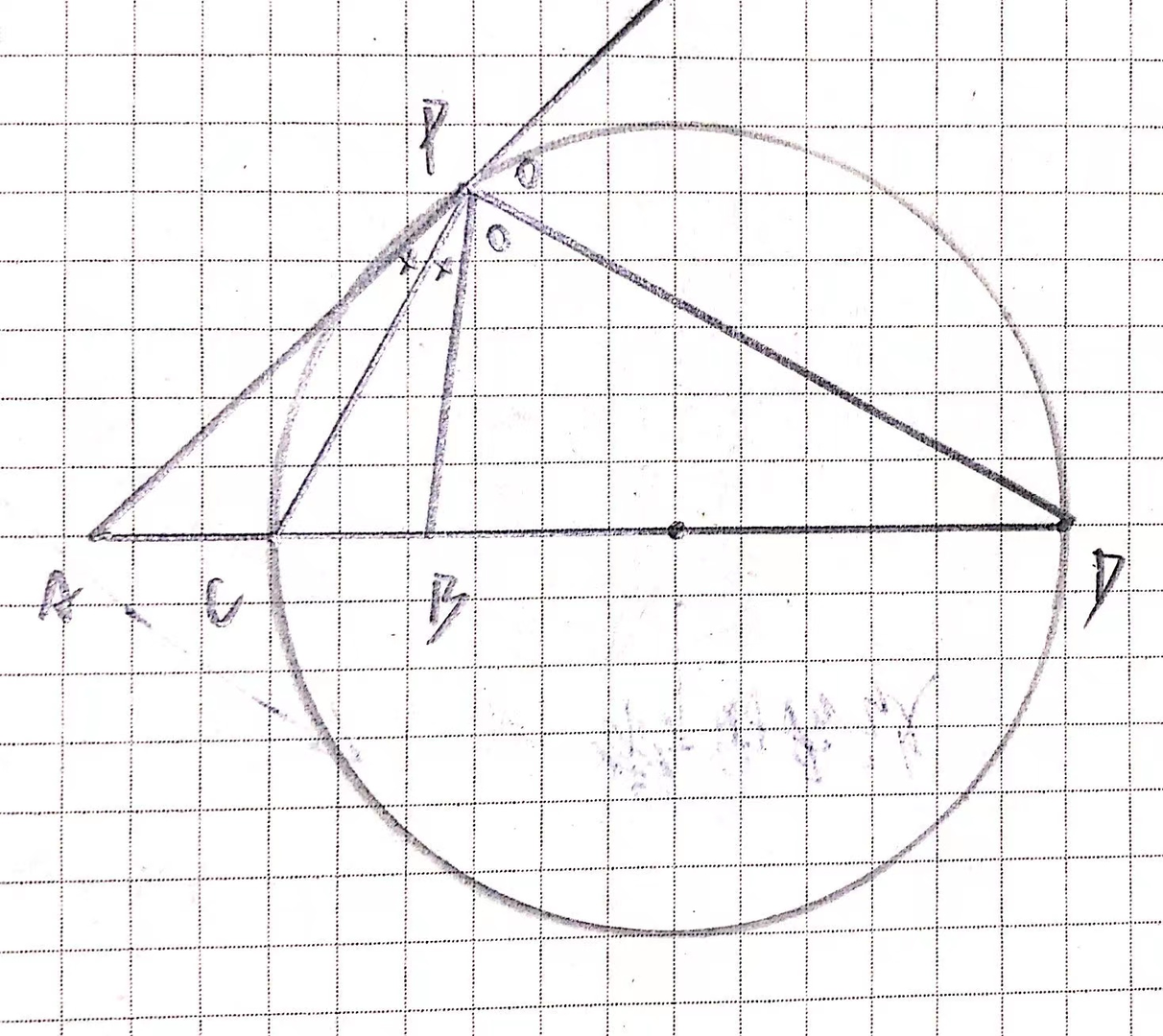
证明:
不妨设 $m>1$,此时 $PD$ 在 $AB$ 延长线上($m<1$ 则反之)。
根据定义,$\dfrac{AC}{BC} =\dfrac{AP}{BP}=\dfrac{AD}{BD}=\dfrac{m}{n}
由角平分线定理,我们知道 PC 是内角平分线,而 PD 为外角平分线。
易知,\angle CPD=90^{\circ},因此 P 在以 CD 为半径的圆上运动。
其完整的证明还需要相似,这里不做过多解释。
阿氏圆的问题变换甚至比胡不归更胜一筹,一般在解决此类问题是常利用相似,创造条件并集中,从而算出答案。
总结与反思
本文的研究就到此结束了。一方面,我将初中主要的最值问题模型进行了列举与讲解,并对一些问题加入了我的想法,有所拓展。
几何的学习离不开敏捷的思维,而最值变换问题则是几何的精华。从以上的研究中,我所用到的方法,其实便是将条件集中再计算的思维。找到关键的突破口,才能解决问题。
另外,由于作者才疏学浅,难免有错误之处,敬请斧正。最值问题还包括代数方面,如函数中的最值问题等,受篇幅所限,不能全部讲完,敬请谅解。
研究过程记录