树状数组学习笔记
Azazеl
·
·
个人记录
一个先学线段树再学树状数组的蒟蒻的树状数组学习笔记
一、前置知识
1.$**任意一个**正整数$x$都可以表示为$x=a_0*2^0+a_1*2^1+a_2*a^2+···+a_n*2^n(a=0$或$1)
简单证明:任何一个十进制数都能表示为二进制数。
E.g:
∵(6)_{10}=(110)_2
∴6=0*2^0+1*2^1+1*2^2
∵(37)_{10}=(100101)_2
∴37=1*2^0+0*2^1+1*2^2+0*2^3+0*2^4+1*2^5
```cpp
x&(-x)
```
简单证明:设一个数$x=1\underbrace{0000···00}_\text{k-1个}
对~x后结果即为~x=0\underbrace{1111···11}_\text{k-1个}
然后再对~x+1=1\underbrace{0000···00}_\text{k-1个}
∴将x&~x+1即为最后一个1的位权.
由于在计算机中十进制数都以补码的形式存储,而负数的补码即为原码~+1
x&-x=x&~x+1
二、树状数组
设:原数组为a,它对应的树状数组为t
其实完全可以把树状数组理解成一个区间内的前缀和,而这个区间划分利用了二进制划分的思想
※我们定义:t_i保存了a[i-lowbit(i)+1]~a[i]的和,即存储了从a[i]开始前面共lowbit(i)个数的和.
E.g:i=6$时:$lowbit(6)=2$,所以$t[6]=a[6]+a[5]
$\ \ \ \ \ A:$因为它高效。
$\ \ \ \ \ $对于共$n$个数的序列,通过这种划分方法我们可以发现这样就只会分出$log\ n$个子区间(证明略),以$8$来举例 ~~(感谢百度百科)~~:
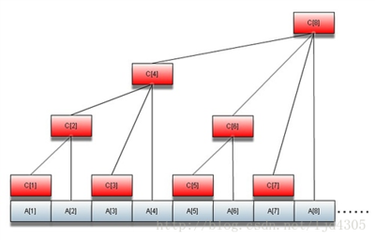
看见了吧,对于每一个$t_i$,它的值即为前面$log i$个树状数组中的元素构成。而对于$n$个元素的序列,树的深度也只有$log\ n$(证明略)。
------------
### 三、性质
(这里我会把一本通上的搬过来加一点点解释)
$1$对于每一个$t_i$,它都等于以它为根节点的所有子树的叶节点的和$($很废话,看看上面的图都会明白$)
(还是很废话,它就是这么定义的)
※$3$除树根外,每一个节点$t_i$其父节点一定是$t_{i+lowbit(i)}
($这里的证明笔者也不是很懂,等有空再研究一下$)
4$对于$n$个元素的序列,树的深度也只有$log\ n
四、代码实现
```cpp
a[100005],t[100005];
```
$2.lowbit$函数
```cpp
int lowbit(int x){return x&(-x);}
```
$3.$单点修改
$\ \ \ \ \ $通过性质$3$,我们可以通过更新该节点及其对应的父节点直到树根,所以只需不断修改点$t_i$并且让$i+lowbit(i)$即可
```cpp
void change(int x,int y){ //给节点x加上y
for(;x<=n;x+=lowbit(x)) t[x]+=y;
}
```
$4.$区间查询
$\ \ \ \ \ $我们求$a[x]$~$a[y]$的和可以转化为$d[y]-d[x-1]$($d$为前缀和)
$\ \ \ \ \ $而我们可以通过将节点$t_i$跳到$t_{i-lowbit(i)}$使它求到该子区间的和
```cpp
int query(int x){//求d[x]
int ans=0;
for(;x;x-=lowbit(x)) ans+=tree[x];
return ans;
}
```
所以$a[x]$~$a[y]$的和即为$query(y)-query(x-1)$即可查询.
------------
### 五、时间复杂度
$\ \ \ \ \ $修改、查询均在最坏情况下为$O(log\ n)$,所以总体为$O((n+m)\ log\ n)$(m为操作次数,包括修改和查询)
------------
### 下面就是毒瘤部分了
### 六、区间修改,单点查询(黄题难度)
前置知识:**差分数组**
我们定义了一个差分数组:$d[]$,差分是一个很强的东西,它可以常数复杂度进行区间修改,但在查询时复杂度比较高
首先我们来看一看差分数组的定义:
$$d[i]=a[i]-a[i-1](i>0,d[0]=a[0]=0)$$
看着很清新脱俗,那我们怎么来操作呢?
我们来看一看怎么查一个数:
$$a[i]=d[0]+d[1]+···+d[i]$$
上面这个式子大家稍微推一推就能得(证)出来(把定义带进去暴算即可)
然后若在数组$a[l]$~$a[r]$这个区间加上$v$,我们怎么做呢?
$$d[l]+=v,d[r+1]-=v$$
上面这个式子大家稍微推一推也能得(证)出来(把上面查询的过程带进去暴算即可)
#### 回归正题
大家不难发现,差分就是在查询时需要统计一次前缀和而时间复杂度比较高,怎么来优化呢?
想想我们讲的树状数组,它可以统计出前缀和,用$O(log\ n)$来代替$O(n)$,优化差分。所以这个时候思路就很明显了:
$$\texttt{用树状数组维护差分数组}$$
以[$P3368$](https://www.luogu.com.cn/problem/P3368)为例
$\mathcal{CODE}
#include <cstdio>
#include <algorithm>
#define ll long long
using namespace std;
const int MAXN=1000005;
ll a[MAXN],d[MAXN],t[MAXN],n;
inline int lowbit(int x){return x&(-x);}
void add(int x,int v)
{
for(;x<=n;x+=lowbit(x)) t[x]+=v;
}
ll query(int x)
{
ll res=0;
for(;x;x-=lowbit(x)) res+=t[x];
return res;
}
int main() {
ll m,zt,l,r,val;
scanf("%lld %lld",&n,&m);
for(int i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
d[i]=a[i]-a[i-1];
add(i,d[i]);
}
for(int i=1;i<=m;i++)
{
scanf("%lld",&zt);
if(zt==1)
{
scanf("%lld %lld %lld",&l,&r,&val);
add(l,val);add(r+1,-val);
}
if(zt==2)
{
scanf("%lld",&l);
printf("%lld\n",query(l));
}
}
return 0;
}