CF2165 全解
JuRuoOIer
·
·
个人记录
翻译均为手翻。
- 11 月 24 日更新:水 uq 时碰到出题人并确认了 F 的一些细节问题。从视频过来的注意一下,一切与视频不符的地方以这里为准。
A. Cyclic Merging
- 知识点:无(当然你可以数据结构硬抗将其思维含量降至 0)。
- 自评:结丹(黄)。
题意
和 P4393 [BalticOI 2007] Sequence 序列问题几乎一致,唯一的区别是本题在环上完成。
依次给定环上的 n 的数,每次可以合并相邻两个数,合并的代价及合并后的值均为两数中较大值。求所有数合并为一个的最小代价。
数据范围:多测,\sum n\le 2\times 10^5,值域 [0,10^9]。
做法
其实一种选择是发现这玩意只开了 2\times10^5 直接开个堆进行模拟,CF 神机怎么跑也过了。
当然更多同学还是选择了正解。考虑在序列上的情况,显然一个数最多贡献两次答案,如果其比左边大贡献一次,比右边大再贡献一次,或者说其实就是每个数和它的下一个数取个 \max 加起来。序列上能做的话环上就是枚举断点然后减掉断点两侧数的 \max 然后就做完了。复杂度线性。
B. Marble Council
每日临门一脚没踹进去:前面都想到了最后被 a simple knapsack dp problem 创飞了喜提没做出来。
题意
给定一个可重集 a,求将 a 划分成若干个可重集后,在划分出的可重集中各取一个众数可能形成的新可重集的数量,对 998244353 取模。
数据范围:多测,\sum n\le 5000,值域 [1,n]。
做法
考虑对每个数拆贡献。然后当你试图考虑贡献怎么算的的时候你会发现:其实这个数只要出现在最终的集合中至少 1 次那么它必然对所有情况都贡献。因为拆多少个集合是随便的,而这个数拆出来的集合只出现它自己就行好。
所以现在只有在最终所得集合中不出现的数需要算算。
然后我们发现一个数字如果出现那每个该数字可以为每个不出现的数值(多个数值显然可以都是众数)提供一个位置。(这边区分一下,相等的多个数算一个数值多个数字,要不然不好表述)
这个条件转化一下,就是出现的数字总个数不小于数字个数最多的数值的数字个数就行。乍一看有点离谱,但其实你分最大的选不选讨论一下就会发现很合理。
然后直接暴力 dp:设 dp_{i,j} 表示前 i 个数值选了 j 个数字的方案数,转移时枚举 j 和当前数值选与不选,最终 j\ge\max cnt_i 的部分贡献答案。复杂度 O(n^2)。
启示:做不出来的时候看看条件能不能转化,尤其是本题根据七字真言已经确定了是 DP 然后你还设不出状态。类似的教训:
- 山大校赛 2024 决赛 I
- NOIP 2021 C
C. Binary Wine
题意
给定长度为 n 的数组 a,你可以进行若干次操作,每次花费 1 代价使 a 中的某个元素增加 1。
- 存在一个长度为 $n$ 的数组 $b$ 使得 $\forall 1\le i\le n,0\le b_i\le a_i$,且 $b_1\oplus b_2\oplus\dots\oplus b_n=c$。
数据范围:多测,$\sum n\le 5\times 10^5$,$\sum q\le 5\times 10^4$,值域 $[0,2^{30})$。
### 做法
按位考虑。首先一位上出现多个 $1$ 显然是不优的。
考虑从高往低枚举每一位。设 $a$ 的各项的这一位求和为 $A$,$b$ 的这一位为 $B$,则分三种情况:
- $A>B$ 时,必然能拿出一个 $a_i$ 给 $b$ 的该位,同时还可以拿出另一个 $a_i$ 则可以覆盖 $b$ 的所有更低位,直接停止枚举输出答案;
- $A=B$ 时,必然能拿出一个 $a_i$ 给 $b$ 的该位,把该 $a_i$ 的该位减掉放回,然后接着枚举后面的位;
- $A<B$ 时,拿不出一个 $a_i$ 了,这时就需要加。而加是要代价的所以我们直接取出 $a$ 里面最大的拿来加。加完了之后该 $a_i$ 就进入第二种情况,即留下一个 $0$。
综上,算法思路就是用一个大根堆维护前 $\log V$ 大的 $a_i$,然后按上面三种情况讨论,其中后两种都每次取堆顶。
# D. Path Split
- 知识点:无。
- 自评:大乘(下位紫)。
### 题意
给定长度为 $n$ 的序列 $a$,求最少将其划分为多少个子序列,使得划分出的每个子序列中相邻两项之差的绝对值均为 $1$。
数据范围:多测,$\sum n\le 10^6$,值域 $[1,2n]$。
### 做法
考虑建图,即每个点向编号比它大且差的绝对值为 $1$ 的所有点连边,这时原题变成了最小路径覆盖。**DAG 最小路径覆盖一般要转化为二分图最大匹配**。
但本题是 $10^6$ 显然直接匈牙利需要大约 $31.71$ 年(不考虑闰年),所以我们要考虑优化。
由于二分图是无向图,所以连边的方式可以改为每个 $i$ 向所有 $a_j=a_i+1$ 的 $j$ 连边,二分图是不变的。
然后发现此时按 $a_i$ 从小往大匹配一定是不劣的。于是这题就变成从小往大枚举 $a_i$ 并尽可能匹配 $a_i+1$ 然后就做到线性(或者 $1\log$,视实现而定)了。
# E. Rainbow Branch
- 知识点:无。
- 自评:真仙(中位紫)。
### 题意
定义一棵边有颜色的树的**不方便度**为其颜色最多的简单路径的颜色数。
给定一棵 $n$ 个点的树,对于每个 $k\in[1,n-1]$ 求当用恰好 $k$ 种颜色(每种都出现)给边染色时该树**不方便度**的最小值。
数据范围:多测,$\sum n\le3\times10^5$。
### 做法
下述距离、路径长度等词一律按边数而非点数。
考虑 $k=n-1$ 的情况,此时答案就是直径。容易想到不方便度的本质就是在颜色数定义下的直径。而直径的中点就是到所有点的最大距离最小的点,此时明显直径长为偶数时的情况比较简单,直径中点到各点间距离均不超过 $\frac{k}{2}$。
从此入手,就是让最外 $\frac{k}{2}-1$ 层每条边分配一种颜色,加上这些层与我们钦定的根结点间的边还要染一种,总共就是所有点到根结点都不超过 $\frac{k}{2}$ 种颜色。由于此时可以钦定任何剩下的点为根结点,所以我们肯定要取度数最大的,因为根据我们刚才的设定每个度数都可以染一种颜色。
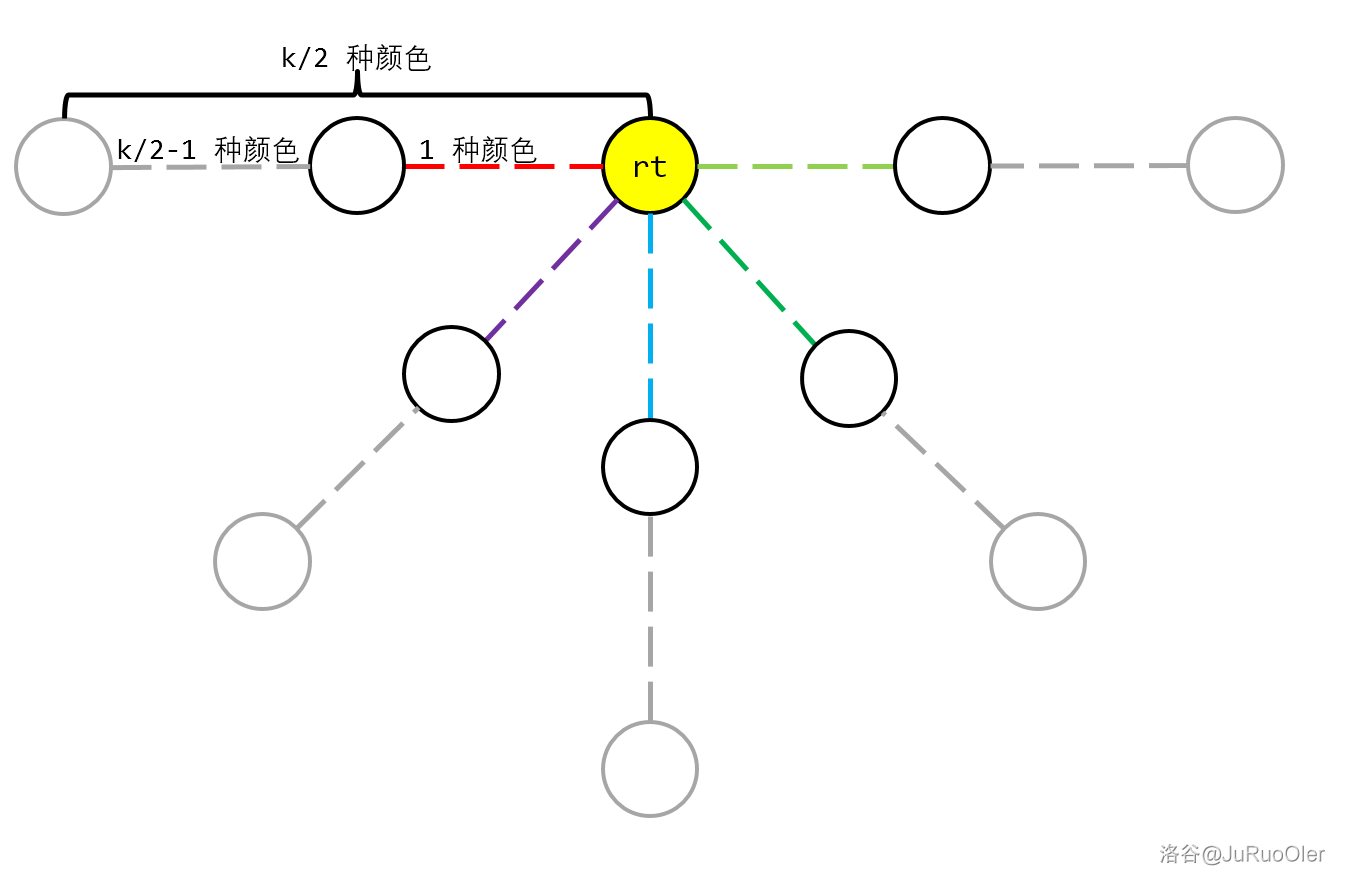
图中虚线表示多个点,灰色的点是被删掉的。
而奇数的情况比较类似,不过此时中点在边上。所以我们让这个边所在的颜色块贡献 $1$ 的答案,于是该颜色块到其他点之间的距离就是不超过 $\frac{k-1}{2}$ 了。
实现时用类似多源 BFS 的方式剥叶子即可。复杂度 $O(n)$。
# F. Arctic Acquisition
- 知识点:线段树。
- 自评:真仙(中位紫)。
### 题意
定义一个序列为**锯齿状的**,当且仅当其存在一个长度为 $5$ 的子序列 $a'$ 使得该子序列的元素按大小升序排序后是 $a'_2,a'_1,a'_4,a'_3,a'_5$。
给定一个长度为 $n$ 的排列 $p$,求其有多少个子区间是**锯齿状的**。
数据范围:多测,$\sum n\le10^6$,值域 $[1,n]$。
### 做法
谁家好人线段树题开 $10^6$ 啊?????
我\*\*的做了 2h 没做出来看眼提示让我扫描线,直接天塌了。只能说过于菜,没一眼秒掉,一旦开始长考基本上就倒闭了。
---
锯齿状的五个点画出来大约是这样的:
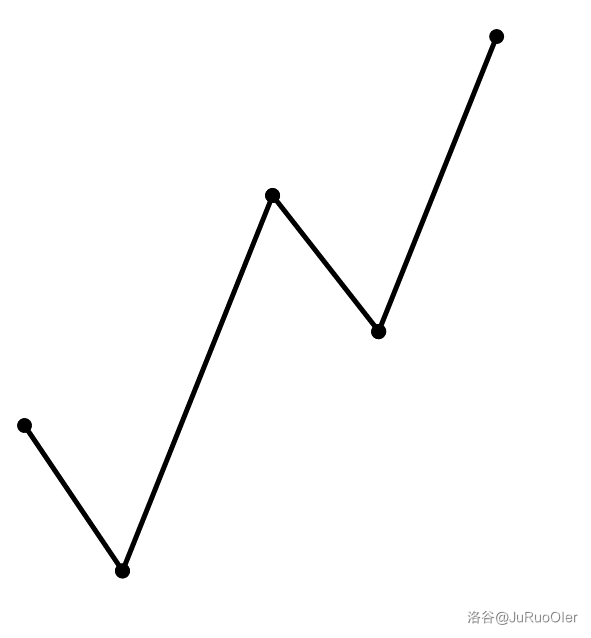
下面说的“第 $k$ 个点”就是上图中从左往右的第 $k$ 个。
首先容易想到的是枚举左端点并求出最靠左的右端点,然后拿这些极小的区间求所有不合法的情况(即包含它们中的任意一个就爆了)。
一旦左端点定了那首先第二个点肯定选右边第一个比它小的,因为从图中可以看出来第二个点的**值对后面的点不构成限制**(因为第一个点的值更大),但下标是有限制的,所以一定是越靠左越好。这个搞棵权值线段树倒着扫一下预处理出来就行。
接下来对后三个点的考虑还是十分常规地当成整体。此时我们对后三个点的限制就是**第四个点要大于第一个点且第三个点要在第二个点后面**,于是考虑维护所有“第三个点”“第四个点”能找到的最小“第五个点”,那原问题就变成一个二维数点了。
但直接维护所有的情况是 $n^2$ 的显然不行,所以考虑只维护极小的,即**不存在将其**从第三个点的下标、第五个点的下标、第四个点的值**三维偏序的其他子区间**。这时有结论:**每个“第四个点”所对应的最优“第五个点”必然是当前“第四个点”后第一个值比其大的**。
题解里那个图是拿来证明的,而且前两种情况一眼可以合并。考虑用一个值在“第四个点”以上、值在“第四个点”“第五个点”之间的点来更新现有的后三个点。
- 新点的值在原“第三个点”以上时,将原“第五个点”替换为新点仍然合法,而这种情况是更优的。
- 新点的值在原“第三个点”以下时,将原“第四个点”替换为新点仍然合法,而这种情况是更优的。
综上结论是正确的。
证明了结论正确后就可以同样用线段树解决问题了。复杂度就是线段树的复杂度即 $O(n\log n)$。