（Ⅳ）梦想协奏曲！迷途之子！！！！！

· · 个人记录

Week 49

7.8

堂堂连载一周年！！！1

7.8

T1 猜到抽屉原理了，别的没猜到。比如只判前缀后缀就可以过。

https://matrix67.com/blog/archives/5182

T2 发现条件相当于每个操作在每个数上最多删一次，要删除次数最大，所以是一个最大流，连出来是一个完全二分图。

考虑转成最小割，上方确定割哪些点之后下方每个点要么直接割，要么把它和没有割的点的连边割完。

T3 对值域倍增分块板子。Ynoi 的 P7447。不会。

考虑暴力维护线段树，每次找出所有最小值大于 x 的区间打标记，然后会被交错的 1 和 10^9 卡。也就是说需要修改的区间会被不需要修改的分开导致复杂度假掉。但如果可以把不需要修改的删掉就能整体打标记。

所以，如果有维护值域在 [B^i, B^{i + 1}) 的线段树，只有大于 B_i 的修改才会分开区间，而这样的修改最多进行 B 次。

具体地，对于一个区间，对于最大值不超过 x 就无影响，最小值离区间下界超过 x 的打标记做普通区间减法，否则递归减去 x，更新所在线段树。

单调修改可以均摊复杂度。比如吉司机线段树。

数据结构题想清楚再写。

7.9

https://codeforces.com/gym/105901/problem/E

怎么找欧拉回路？？？？

https://codeforces.com/gym/105901/problem/J

https://codeforces.com/gym/105901/problem/D

https://codeforces.com/gym/105257/problem/J

https://qoj.ac/contest/1913/problem/9042

https://codeforces.com/problemset/problem/1578/B

7.10

T1 由于神秘原因一直跑不出大样例，调空气调了三个小时未果心态爆炸。赛后发现是小熊猫 C++ 设置的栈空间把写的扩栈命令覆盖掉了，，，小熊猫害人不浅，，，，

T4 是区间内每个数出现 k 次的集合哈希板子。忘记了。

T2 将 A 到下一个 C 之间的 B 和 A 分成一段，BC 同理，发现每一段之间是能够做到没有影响的，因为可以将 A 段中的 A 看作能打败本段的 A 且无法打败下一个 C 段中的 A。所以每段内相当于做冒泡排序。如果结尾段无法打败开头段就先打 n 轮。

号家军成都分舵 2025 暑假成都信息学研学营

让我掉下眼泪的 不止昨夜的酒
让我依依不舍的 不止你的温柔
余路还要走多久 你攥着我的手
让我感到为难的 是挣扎的自由
分别总是在九月 回忆是思念的愁
深秋嫩绿的垂柳 亲吻着我额头
在那座阴雨的小城里 我从未忘记你
成都 带不走的 只有你
和我在成都的街头走一走
直到所有的灯都熄灭了也不停留
你会挽着我的衣袖 我会把手揣进裤兜
走到玉林路的尽头 坐在小酒馆的门口
分别总是在九月 回忆是思念的愁
深秋嫩绿的垂柳 亲吻着我额头
在那座阴雨的小城里 我从未忘记你
成都 带不走的 只有你
和我在成都的街头走一走
直到所有的灯都熄灭了也不停留
你会挽着我的衣袖 我会把手揣进裤兜
走到玉林路的尽头 坐在小酒馆的门口
和我在成都的街头走一走
直到所有的灯都熄灭了也不停留
和我在成都的街头走一走
直到所有的灯都熄灭了也不停留
你会挽着我的衣袖 我会把手揣进裤兜
走到玉林路的尽头 走过小酒馆的门口

Week 50

Day -1（7.11）

玩原神。

两周玩不了原神了，，，

Day 0（7.12）

高铁转大巴到成外。四人寝，有卫浴，有桌子，有空调，有插座，没网。柜子可以藏人。

此时我还没意识到为什么柜子可以藏人。

狼人杀。

食堂平均水平不如南开半个窗口的下限。自助餐的意思是不限量。

所有考试题都是高质量题目。

没收电子设备。22:30 熄灯。

一位先人对这个集训的评价：

580 一天的网吧

Day 1（7.13）

6:40 起床。

分班考，考到 J 组了。

没有评测。sjx 评讲。

T1 P11598。不难发现 a_i'\in \{ a_i, a_{i - 1}' \pm d, a_{i + 1}' \pm d\}，所以 a_i' \in \{ a_j + x \cdot d \}~~(x \in [-n, n])，单调队列优化即可。Slope Trick。

T2 原题没补。UVA1439。\min\limits_{\text{定向}}\{ \text{最长链长度} \} = \min\limits_{\text{定向}}\{ \min\limits_{\text{划分}}\{\text{层数}\} \} = \min\limits_{\text{划分}}\{\text{层数}\}，后面忘了。

Dilworth 定理。

DAG 中最长反链长度等于最小链覆盖数，最长链长度等于最小反链覆盖数。

其中反链指互相没有连边的点集。

T3 UVA1204。先考虑链，是状压求哈密顿路径。

T4 DP，但是有环，所以预处理或者跑 SPFA。

DP 专场。

本题已通过，答案不再显示。

Day 2（7.14）

数据结构选讲——sjx。

P4198 线段树维护前缀最值。https://www.cnblogs.com/PinkRabbit/p/Segment-Tree-and-Prefix-Maximums.html

这里本来有一段解释，但因为随机关机就和成外的母亲一起消失了。

总之就是更新线段树区间的时候再用 \log n 的复杂度递归计算一次，复杂度 \mathcal O(n \log^2 n)。

考虑一个类似吉司机线段树的东西，就可以做到单 \log。https://www.luogu.com.cn/discuss/391125

然后就可以做 at_joisc2014_i 了。

LOJ6029。

对于一个区间，加法不会改变其极差，而 \log 次除法就可以使得极差 \le 1。

具体地，只需要维护加法的 tag，除法在极差 > 1 时暴力，复杂度就是均摊 \mathcal O(q \log n \log V)。

P8990。

众所周知的，树上一个点集形成的连通块数量等于点数减去边数。

所以答案就是所有未点亮点形成一个连通块的时刻的点亮点形成的连通块数量之和，线段树维护。

区间切割。

因为修改是单调的，所以可以搞一个类似减半警报器的东西，保证每个区间最多被重构 \log 次。

Day 3（7.15）

树上问题——yyh。

树形 DP，换根 DP（Hash），树上背包（复杂度），树上倍增（动态 DP），度数分治，重链剖分（DSU on tree），长链剖分（k 级祖先，优化 DP），树的直径（树的中心），树的重心。

点分治、虚树、LCT 没有讲。可能因为用的是 NOIP 的课件。

因为每个子树独立性比较强，所以比较适合 DP，也有天然的阶段。

DSU on tree，即 DP 时继承重儿子信息，暴力枚举轻子树节点。复杂度为轻子树总大小 \mathcal O(n \log n)，因为每个点最多被枚举 \log 次。

长链剖分优化 DP，即 DP 关于深度的信息时继承重儿子，暴力合并轻儿子信息。复杂度为长链长度之和 \mathcal O(n)。

P3177。

不难发现贡献仍然可以在子树内独立统计，相当于费用提前计算。

HDU6035。

巧妙的做法见 https://www.luogu.com.cn/article/61rei9t8，但是直接上虚树也可以做。

AT_arc101_c。

设状态为子树内未配对点数量，合并两个子树时枚举两个子树内配对点对数量和各自剩余点数量，复杂度 \mathcal O(n ^ 3)。

考虑容斥，钦定若干条边未被覆盖，容斥系数 (-1)^{\vert E \vert} 在合并时计算。状态改为子树内连通块大小，复杂度 \mathcal O(n ^ 2)。但凡系数带个组合数都不能这么算。

我错了。组合数可以递推，所以也可以放到信息里。

无根树中以直径中点，中间一条边，重心，或者直径本身，作为根可能会有更好的性质。

Day 4（7.16）

T1 错排问题，考虑钦定。

T2 二分之后是单调的，可以均摊复杂度。

T3 二分答案 \le m 后，设 \le \dfrac{m}{2} 为 0，> \dfrac{m}{2} 为 1，两个 0 必然可以相邻，两个 1 必然不能相邻。所以答案一定 0 全选，两个 0 之间最多一个 1。

杂题选讲——hfy。

交互，构造，数学。Ad-hoc。

构造 A 到 B 的方案，且操作可逆，考虑找特殊的中间状态 M 构造 A 到 M 和 M 到 B 的方案。

有意思的东西。指随机算法和近似算法。max-SAT。https://www.cnblogs.com/cwhfy/p/18751355

有趣的东西。算了。

闲话。CF 打不上去了。proprocessor。初二 NOIP 预处理阶乘没写 1LL，四川二十多名，不然进省队了。

Day 5（7.17）Slope Trick

DP 选讲——hfy。

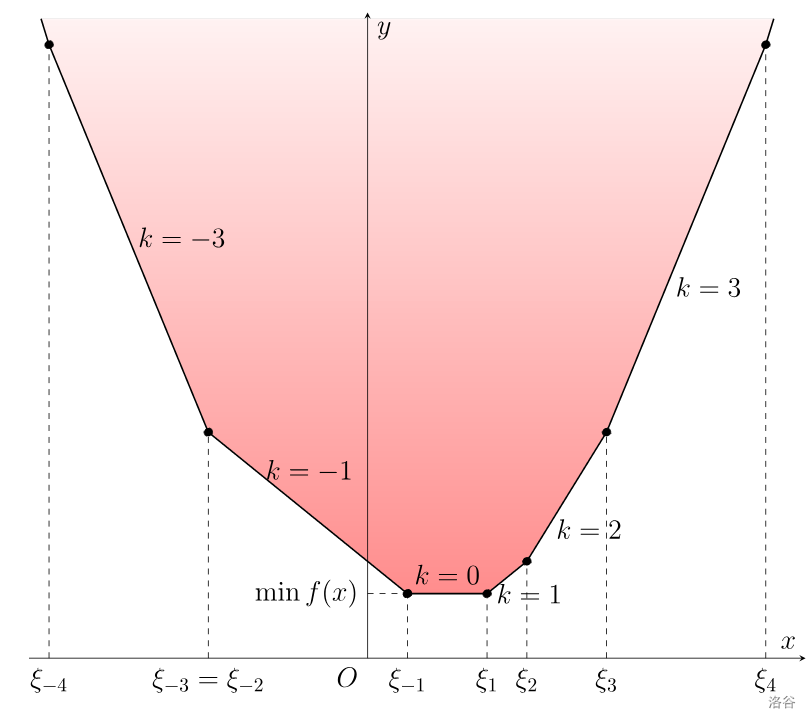
--- SlopetRick 就是说对于 $f_{i, j}$ 直接维护 $f_i(j)$ 的图像，转移时考虑斜率的变化。通常维护凸函数，因为其有较好的性质，比如两个凸函数的非负线性组合或闵可夫斯基和还是凸函数。 具体地，如果斜率的绝对值较小，考虑维护最小值和每个拐点，便于计算两个凸函数直接相加。 ![](https://cdn.luogu.com.cn/upload/image_hosting/g3djkv76.png) 注意图中的 $\xi_{-3} = \xi_{-2}$，斜率变化了 $2$。 用两个堆维护顶点两侧的拐点，再记录最右侧的函数为 $kx + b$。相加时 $k$ 和 $b$ 直接相加，拐点集合直接合并再保证右侧拐点数量为 $k$。 还可以维护斜率，便于计算两个凸函数做闵可夫斯基和，即 $(\min, +)$ 卷积。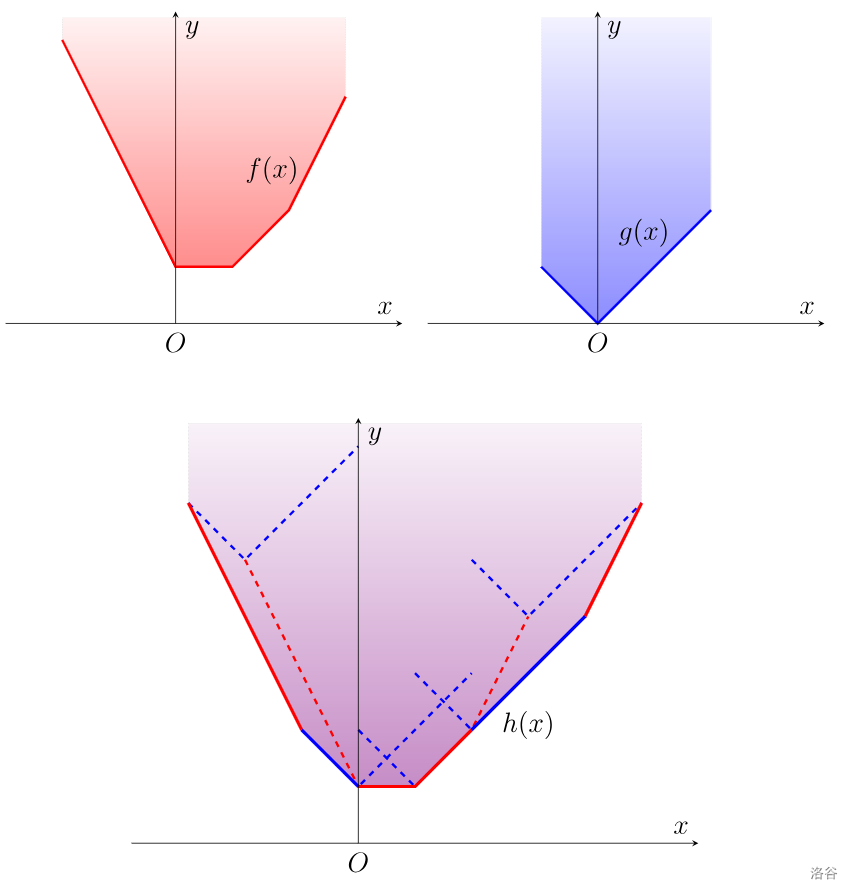 ![](https://cdn.luogu.com.cn/upload/image_hosting/1vl9e6to.png) 几何意义是将一个函数沿另一个函数平移。 观察图示，不难发现原来两个函数的每段斜率都在闵可夫斯基和中出现并从小到大顺次连接，可以直接启发式或归并地把一个函数的斜率插入到另一个函数。具体实现上可以维护顶点坐标和每一个单位区间上的斜率。 --- 在线决策单调性。 若 $f_i = \min \{ f_j + w(j, i) \}$ 中 $w(j, i)$ 满足四边形不等式，即转移矩阵为蒙日阵，则 $f$ 的决策点具有单调性。 如果当前已经得出了每个决策点的转移区间，加入新的决策点时就需要从后往前尝试覆盖区间。 --- https://qalxry.github.io/2024/01/20/【算法】DP优化总结/#d1d-决策单调性优化 https://www.cnblogs.com/p-b-p-b/p/15054179.html --- 需要二分单调栈的题目满足四边形不等式，但是没有决策单调性。 不满足。lwc 说的。 有决策单调性。lwc 说的。 不可能有除了柠檬外的二分单调栈。lwc 说的。 --- $\overset{\tiny\text{DP of DP}}{\footnotesize\textrm{DP 套 DP}}$。内层 DP 刷表。 如果 $w(l, r)$ 表示区间内合法子串数量，则必然满足四边形不等式。 wqs 二分后是在线决策单调性，区间代价可以 CDQ 分治套整体二分套莫队。 笛卡尔树。算了，我忘了。不讲了。区间 max 和区间 min。很有用的。嗯。就讲完了。 近似算法，随机算法。DP 不如 AB=C 有用。$1.5-10^{-36}$ 近似 TSP。 --- 疯狂星期四。没有汉堡。 ## Day 6（7.18）扩展 min-max 容斥 DP 优化——xzc。sjx 正在共享屏幕。正在讲话：yyh。 优化状态，优化转移。 --- 线段树套李超树。单点改区间查都是 $\log^2$。李超树维护线段也是 $\log^2$。 树套树因为无法合并信息，所以只能单点改区间查或区间改单点查。 考虑在每个重链上做 CDQ 分治。 出栈序。 或者发现重链剖分一条路径会得到 $1$ 个区间和 $\log$ 个前缀，对每个前缀预处理即可。 --- 加入 $(a, b)$，给定 $(x, y)$ 查 $\max\{ax + by\} = x \cdot \max\left\{a + b \cdot \dfrac{y}{x}\right\}$，李超线段树。 加入 $(a, b, c)$，给定 $(x, y)$ 查 $\max\{ax + by + c\}$。四分李超线段树？？？ --- min-max 容斥。本质是 $\min(a, b) = a + b - \max(a, b)$。 $\max\limits_{i \in S} x_i = \sum\limits_{\substack{T \subseteq S \\ T \neq \varnothing}} (-1)^{\vert T \vert - 1} \min\limits_{j \in T} x_j \min\limits_{i \in S} x_i = \sum\limits_{\substack{T \subseteq S \\ T \neq \varnothing}} (-1)^{\vert T \vert - 1} \max\limits_{j \in T} x_j

将第 k 小数映射为 f(k) = \{1, 2, \cdots , k\} 后，f(\max(a, b)) = f(a) \cup f(b)，f(\min(a, b)) = f(a) \cap f(b)，由容斥原理易证。

主要用于计算最值的期望。

扩展 min-max 容斥。

\underset{i \in S}{\operatorname{kthmax}}~x_i = \sum\limits_{\substack{T \subseteq S \\ T \neq \varnothing}}(-1)^{|T| - k} \cdot \dbinom {|T| - 1}{k - 1} \cdot \min\limits_{j \in T}{x_j} \underset{i \in S}{\operatorname{kthmin}}~x_i = \sum\limits_{\substack{T \subseteq S \\ T \neq \varnothing}} (-1)^{|T| - k} \cdot \dbinom {|T| - 1}{k - 1} \cdot \max\limits_{j \in T}{x_j}

证明：https://www.luogu.com.cn/article/t2zqvdou

不妨设 \underset{i \in S}{\operatorname{kthmax}}~x_i = \sum\limits_{T \subseteq S} F(\vert T \vert) \min\limits_{j \in T}{x_j}，x_i > x_{i + 1}，\vert S \vert = n。

考虑 x_j 对 \underset{i\in S}{\operatorname{kthmax}}~x_i 的贡献，我们希望其等于 [j = k]。

而 x_j 在所有 \vert T \vert = t 中作为 \min 出现的次数为 \dbinom{j - 1}{t - 1}。

所以 [j = k] = \sum\limits_{t = 1}^n \dbinom{j - 1}{t - 1} \cdot F(t)。

设 g(j) = [j + 1 = k]，f(t) = F(t + 1)，就有 g(j) = \sum\limits_{t = 0}^{j} \dbinom{j}{t} f(t)

由二项式反演得 f(t) = \sum\limits_{j = 0}^{t} \dbinom{t}{j} (-1)^{t - j} g(j)。

即 F(t + 1) = \sum\limits_{j = 0}^{t} \dbinom{t}{j} (-1)^{t - j} [j + 1 = k] = \dbinom{t}{k - 1} (-1)^{t - (k - 1)}。

也就是 F(t) = \dbinom{t - 1}{k - 1} (-1)^{t - k}。得证。

不难猜到扩展 min-max 容斥仍然在期望意义下成立。就可以做 P4707 了。

m \cdot \sum\limits_{T} (-1)^{|T| - k} \cdot \dbinom{|T| - 1}{k - 1} \cdot \dfrac{1}{\sum\limits_{j \in T} p_j}

如果设状态为所有大小为 t 的集合的 \dfrac{1}{\sum\limits_{j \in T} p_j} 之和，这个东西是不好转移的。

发现 m \le 10^4。考虑把状态改成所有 \sum\limits_{j \in T} p_j = s 的集合的 (-1)^{|T| - k} \cdot \dbinom{|T| - 1}{k - 1} 之和。这个东西有 k \le 11 的性质。

考虑原来的一个集合 T 的贡献为 (-1)^{|T| - k} \cdot \dbinom{|T| - 1}{k - 1}，加入 p_i 后贡献转为 (-1)^{|T| + 1 - k} \cdot \dbinom{|T|}{k - 1}。

然后集中注意力，发现 -1 和组合数都是可以递推的。

\begin{aligned} & (-1)^{|T| + 1 - k} \cdot \dbinom{|T|}{k - 1} \\ = & (-1)^{|T| - (k - 1)} \cdot \left( \dbinom{|T| - 1}{k - 2} + \dbinom{|T| - 1}{k - 1} + [|T| = 0 \land k = 1] \right) \\ = & (-1)^{|T| - (k - 1)} \cdot \dbinom{|T| - 1}{k - 2} - (-1)^{|T| - k} \cdot \dbinom{|T| - 1}{k - 1} + [|T| = 0 \land k = 1] \\ \end{aligned}

其中，为了避免负数意义下的组合数，定义

\dbinom{n}{m} = \begin{cases} \dfrac{n!}{m!(n - m)!} & n \ge 0 \land m \ge 0 \land n \ge m \\ 0 & \text{otherwise} \end{cases}

所以 f_{s, k} \gets f_{s, k} + f_{s - a_i, k - 1} - f_{s - a_i, k} + [s = a_i \land k = 1]。

这个题也太好了。简直就是我做过最好的容斥题。

广义快速扩展超级万能 min-max 容斥 pro max ultra。

\underset{i \in S}{\operatorname{kthmax}}~\dfrac{x_i}{i!}x^i = \sum\limits_{T \subseteq S} (-1)^{|T| - k} \cdot \dbinom {|T| - 1}{k - 1} \cdot \min\limits_{j \in T}{\dfrac{x_j}{j!}x^j}

lwc 写的。

AT_abc221_g。

第 i 次从 (x, y) 走到 (x \pm d_i, y) 或 (x, y \pm d_i)，不好。

把曼哈顿转成切比雪夫，从 (x, y) 走到 (x \pm d_i, y \pm d_i)，横纵坐标就独立了。

Day 7（7.19）

喝了 MikeZ 代购的红牛之后终于想出一次正解，，，泪目了。

T3 数据结构。

发现如果把所有区间画成一个 n \times n 的等腰直，那么每个区间作为最大子段的所有区间在图上作为一个矩形且互不相交。但因为矩阵个数是 \mathcal O(n ^ 2) 的并没有什么用。

在路上发现了成外私斋社。为什么会有死宅参加社团？？？都是现充。

晚上吃南朝鲜自助烤肉。

笑点解析：进商场后问这是几楼。

7.20

眉山三苏祠。

春熙路。没有发现和四川有关的东西。

上午玩 PS5 胡闹厨房。♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿冲刺！♿

下午玩桌游忍者之夜。对等人数暗牌博弈，推理程度不如狼人杀。

发现了若干没学过或不太会的东西，包括不限 Slope Trick，Dilworth 定理，前缀最值线段树，DSU on tree，长链剖分，二项式反演，带容斥系数 DP，闵可夫斯基和，在线决策单调性，出栈序，扩展 min-max 容斥。

没学过的几个简单写一下。Slope Trick 的核心在于把 DP 信息当成函数做整体维护，前缀最值线段树在区间合并时以 \log 复杂度计算信息，min-max 容斥主要用于在期望意义下转换最值。

本周课程集中于 DP 和数据结构。

其中计数题都不太会做，尤其是容斥反演的 DP。下周好像有组合计数专题。

由于概率学原因在暑假已经做到至少五道均摊复杂度的数据结构题了。共同点就是修改有单调性，因为均摊不能做持久化。

上数据结构的时候先想清楚修改什么，查询什么，有没有性质，而不是选了数据结构直接套上去。好的情况多一个 \log，一般情况写不出来，坏的情况根本做不了。

作业表加了巨量题目，但很多好题还不太会或者没写。后面几天大部分时间都用来学科技了，题还要等之后补。

三场模拟赛打得一般。可能是因为没睡好还没有东鹏特饮。省选级的难题还是不太能做得出来，也因为现在才真正开始大量做这种题。

想到还要在这个成外待一周这件事本身比吃一周食堂的饭难受。

Week 51

岁月在默数三四五六 第六天以后
人们开始存在宇宙 黑夜和白昼
呼吸第一口气的咽喉 最怕命运小偷
坏和美好我用血肉 去感受
问宿命是否 再多久 再持久 再永久
抵不了不朽
恋人从挥手 到牵手 到放手 到挥手
就该足够
对夜的长吼 我胸口 的伤口 随风陈旧
你我终会沦为尘埃漂流
等待花季烟雨稠
再化降水驻守
属于你的愿与愁
时间在倒数你在左右 多想踩碎沙漏
但能同时在同个宇宙 就不求滞留
呼吸下一口气的预谋 终究会被没收
漫天风雪我陪你颤抖 我们别回头
问宿命是否 再多久 再持久 再永久
抵不了不朽
恋人从挥手 到牵手 到放手 到挥手
就该足够
对夜的长吼 我胸口 的伤口 随风陈旧
你我终会沦为尘埃漂流
等待花季烟雨稠
再化降水驻守
属于你的愿与愁
能爱多久 想多久 是多久 是永久
爱过就不朽
那我不走 不分手 不放手 不挥手
十指紧扣
分岔路口 我伤口 贪与渴求
渺小微弱像尘埃漂流
等待花季烟雨稠
再化降水驻守
属于你的愿与愁
分岔路口 我胸口 的伤口 贪与渴求
渺小微弱像尘埃漂流
等待花季烟雨稠
再化降水驻守
只为重逢的时候

Day 8（7.21）

图论选讲——hfy。

强化限制以得到更好的性质。

欧拉回路。

Johnson 全源最短路。

核心思想是给每个点赋势能 h_i，把 u \to v 的边权改为 w + h_u - h_v。不难发现其仍然可以求出正确的最短路长度，而我们就可以以此对边权做一定调整。

CF843D。

因为每次给一些边权加 1，考虑利用上一轮的信息。设这一轮起点到 $i$ 的最短路增加量为 $\Delta_i$，则有转移 $\Delta_v = \min\limits_{u \to v} d_u + \Delta_u + w - d_v$，也就是把边权改为 $w + d_u - d_v$。因为 $\Delta \le n$，就可以做 $\mathcal O(m)$ 的最短路。 --- P9257。 好题，除了最后搜索的部分。 --- P9731。 P7831。 P9732。 双极定向，支配树，最小树形图，最小割树。明天讲。 $\sum\limits_{i = 1}^n \sum\limits_{j = 1}^m d(i \oplus j \oplus x)$，$n, m, x \le 10^{10}$。枚举 $i$ 与 $n + 1$ 首个不同的位置。 ## Day 9（7.22）上下界网络流 qoj7514。 --- 网络流。 Hall 定理。二分图匹配转最小割。CF600F。 --- 上下界网络流，每条边的流量有上下界限制。 不难想到给每条边预分配其下界的流量再进行调整。分配后每个点的流量可能剩余或缺少，为了让网络自行调整，建立超级源点和汇点，由超级源点连剩余点，缺少点连向超级汇点。 因为流量守恒，这样求出最大流后如果跑满，加上预分配的流量就是对的，得到**无源汇可行流**。 对于**有源汇可行流**，源点和汇点不用流量守恒，从汇点向源点连容量无穷的边。 在跑完可行流的残图上跑最大流，可以对现有边权反悔，得到**有源汇最大流**。 同理，由汇点到源点反悔得到**有源汇最小流**。 把最大流改成费用流得到上下界有源汇费用流。 跑最大流得到的是可行流，跑最小费用最大流得到的是**有源汇最小费用可行流**。P4043。 **有源汇最小费用最大流**。只要没有负环费用流跑出来就是对的。 为什么没有无源汇最大流？ > 首先，我们发现我们还没有定义无源汇网络的最大流/最小流是什么，然后再想一想，发现它们没有什么意义。所以我们就做完了。——Just_int_mian --- 然后就可以做负环费用流了。 考虑一条费用为负的边，先将其强制流满，就变成了反悔这条边需要费用。 --- 静态/动态模拟费用流。 --- 最小割数学模型。 最小割并不能很方便地建模数学问题的原因在于边权必须非负。否则就可以直接建出一个点和它的反点了。 所以我们希望贡献最大，代价最小。 ![](https://cdn.luogu.com.cn/upload/image_hosting/nla4g1ja.png "网络流的图不用 windows 画图都是异端。") | u | v | 代价 | 贡献 | |:-:|:-:|:-: |:-: | | S | S | $d$ | $a + b + c$ | | S | T | $a + b + d$ | $c$ | | T | S | $a + c + d$ | $b$ | | T | T | $a$ | $b + c + d$ | 四个方程四个未知数。但 $a$ 和 $d$ 必须是非负数。考虑反转一些点的状态。 AT_agc038_f。 ISAP 会被卡。要写 Dinic。 ## Day 10（7.23） 这个红牛也太好喝了，，， T2 结论有问题，但是过了。 ![](https://cdn.luogu.com.cn/upload/image_hosting/65x43wn0.png) 考虑以直径中间一条边为根，每个点距离最远的点就是另一棵树中深度最大的点。 那么每条不经过根的路径的高度就是 LCA 到另一棵树中深度最大的点的距离。如果经过根就可以分开处理。 T3 P9194。 每次删除一个点并将与其相邻的点两两连边。 我们认为原题中所有点是黑点，并且在黑点间的边上添加一个白点。 删除点时，与这个点相邻的白点全部被合并成了一个白点，那么两个黑点之间有边的条件就是存在一个白点与这两个黑点相邻。 --- ![](https://cdn.luogu.com.cn/upload/image_hosting/lc21kd8q.png) 这是 wxir。 ![](https://cdn.luogu.com.cn/upload/usericon/783628.png) 这是 exit。 ## Day 11（7.24）斯特林数、单位根反演 数学专题应用。 --- 斯特林数。 第二类斯特林数 $\displaystyle{n \brace k}$，组合意义为将 $n$ 个不同元素划分为 $k$ 个非空相同集合的方案数。 设 $f(k)$ 为将 $n$ 个不同元素划分为 $k$ 个可空不同集合的方案数，有 $f(k) = k^n$。 设 $g(k)$ 为将 $n$ 个不同元素划分为 $k$ 个非空不同集合的方案数，有 $f(k) = \sum\limits_{i = 0}^k \dbinom{k}{i} g(i)$。 由二项式反演，$g(k) = \sum\limits_{i = 0}^k \dbinom{k}{i} (-1)^{k - i} f(i) = \sum\limits_{i = 0}^k \dbinom{k}{i} \cdot (-1)^{k - i} \cdot i^n$。 设 $\displaystyle{n \brace k}$ 为将 $n$ 个不同元素划分为 $k$ 个非空相同集合的方案数，有 $\displaystyle{n \brace k} = \dfrac{g(k)}{k!}$。 --- ![](https://cdn.luogu.com.cn/upload/image_hosting/omwbizdf.png) $P$ 是分拆数的意思。 只有球异非空的时候才可以从盒异除以 $m!$ 得到盒一样。 因为球同的时候每个盒同的方案中装有数量相同的球的盒子是相同的，并不会被在盒异时被算 $m!$ 次。球异时空盒子也是相同的。只有球异非空的时候才能保证每个盒子互不相同。 所以其它情况下盒异到盒同会较为困难，不能直接转化。 --- 有 $\displaystyle{n \brace k} = \dfrac{g(k)}{k!} = \dfrac{\sum\limits_{i = 0}^k \dbinom{k}{i} \cdot (-1)^{k - i} \cdot i^n}{k!} = \sum\limits_{i = 0}^k \dfrac{(-1)^{k - i} \cdot i^n}{i! \cdot (k - i)!}$，就得到了第二类斯特林数的通项公式。 考察其组合意义，不难发现其递推公式 $\displaystyle{n \brace k} = \displaystyle{n - 1 \brace k - 1} + k \cdot \displaystyle{n - 1 \brace k}$。 这个递推式相当于把每个盒子按其中球的最小编号排序，所以是盒同。 --- 定义第一类斯特林数 $\displaystyle{n \brack k}$，组合意义为将 $n$ 个不同元素划分为 $k$ 个非空相同轮换的方案数。 考察其组合意义，不难发现其递推公式 $\displaystyle{n \brack k} = \displaystyle{n - 1 \brack k - 1} + (n - 1) \cdot \displaystyle{n - 1 \brack k}$。 --- 定义上升幂 $x^{\overline{n}} = \prod\limits_{k = 0}^{n - 1} (x + k)$，下降幂 $x^{\underline{n}} = \prod\limits_{k = 0}^{n - 1} (x - k)$。 因为 $\displaystyle f(k) = k^n = \sum\limits_{i = 0}^k \dbinom{k}{i} g(i) = \sum\limits_{i = 0}^k \dbinom{k}{i} \displaystyle{n \brace i} i! = \sum\limits_{i = 0}^k \dfrac{k!}{(k - i)!} \displaystyle{n \brace i} = \sum\limits_{i = 0}^k k^{\underline{i}} \displaystyle{n \brace i}$， 得到普通幂转下降幂公式 $x^n = \sum\limits_{k = 0}^n \displaystyle{n \brace k} x^{\underline{k}}$。 把普通幂转为阶乘后再乘组合数就有比较好的性质。 比如 $x^n \dbinom{m}{x} = \displaystyle\sum\limits_{k = 0}^n \displaystyle{n \brace k} x^{\underline{k}} \dbinom{m}{x} = \sum\limits_{k = 0}^n \displaystyle{n \brace k} \dfrac{m!}{(x - k)!(m - x)!} = \sum\limits_{k = 0}^n \displaystyle{n \brace k} \dfrac{m!}{(m - k)!} \dfrac{(m - k)!}{(x - k)!(m - x)!} = \sum\limits_{k = 0}^n \displaystyle{n \brace k} m^{\underline{k}} \dbinom{m - k}{x - k}$。 --- P6620。 首先把多项式转为下降幂多项式。P5383。但这道题 $m \le 1000$，可以暴力展开。 $$ \begin{aligned} & \sum_{k = 0}^n f(k) \cdot x^k \cdot \dbinom{n}{k} \\ = & \sum_{k = 0}^n \sum_{i = 0}^m b_i \cdot k^{\underline{i}} \cdot x^k \cdot \dbinom{n}{k} \\ = & \sum_{i = 0}^m b_i \sum_{k = 0}^n \dfrac{k!}{(k - i)!} \cdot \dfrac{n!}{k!(n - k)!} \cdot x^k \\ = & \sum_{i = 0}^m b_i \sum_{k = 0}^n \dfrac{n!}{(k - i)!(n - k)!} \cdot x^k \\ = & \sum_{i = 0}^m b_i \cdot n^{\underline{i}} \sum_{k = 0}^n \dbinom{n - i}{k - i} \cdot x^k \\ = & \sum_{i = 0}^m b_i \cdot n^{\underline{i}} \cdot x^i \sum_{k = 0}^{n - i} \dbinom{n - i}{k} \cdot x^k \\ = & \sum_{i = 0}^m b_i \cdot n^{\underline{i}} \cdot x^i \cdot (x + 1)^{n - i} \\ \end{aligned} $$ --- https://zhuanlan.zhihu.com/p/65424997 https://www.luogu.com/article/83ub0lvq https://www.cnblogs.com/alex-wei/p/Dirichlet.html 繁衍的本质：在生物学角度上看，繁衍是一种生物本能，是每个个体为了传递自己的遗传信息而追求的目标。 反演的本质： 有 $f(n) = \sum\limits_{i = 0}^n a_{n, i} \cdot g(i)$，$g(n) = \sum\limits_{i = 0}^n b_{n, i} \cdot f(i)$。 那么 $f(n) = \sum\limits_{i = 0}^n a_{n, i} \sum\limits_{j = 0}^i b_{i, j} \cdot f(j) = \sum\limits_{j = 0}^n f(j) \sum\limits_{i = j}^n a_{n, i} \cdot b_{i, j}$。 所以 $[j = n] = \sum\limits_{i = j}^n a_{n, i} \cdot b_{i, j}$。 然后就可以证反演了。 $\displaystyle \sum_{i = j}^n (-1)^i \dbinom{n}{i}(-1)^j\dbinom{i}{j} = \dbinom{n}{j} \sum_{i = j}^n (-1)^{i - j} \dbinom{n - j}{i - j} = \dbinom{n}{j} \sum_{i = 0}^{n - j} (-1)^i \dbinom{n - j}{i} = \dbinom{n}{j} 0^{n - j} = [j = n]

P6031。

斯特林反演。

\displaystyle f(n) = \sum_{i = 0}^n (-1)^i \cdot {n \brace i} \cdot g(i) \iff f(n) = \sum_{i = 0}^n (-1)^i \cdot {n \brack i} \cdot f(i)

类欧几里得算法。怎么求 \max\limits_{x} \left\{A x + B \left\lfloor \dfrac{px}{q} \right\rfloor \right\}？？？

单位根反演。

由单位根的几何意义可证。 $$ \begin{aligned} & i \bmod k \\ = & \sum_{j = 0}^{k - 1} j \cdot [i \bmod k = j] \\ = & \sum_{j = 0}^{k - 1} j \cdot [k \mid (i - j)] \\ = & \sum_{j = 0}^{k - 1} j \cdot \frac{1}{k} \sum_{t = 0}^{k - 1} \omega_{k}^{(i - j) t} \\ = & \sum_{j = 0}^{k - 1} j \cdot \frac{1}{k} \sum_{t = 0}^{k - 1} \omega_{k}^{i t} \omega_{k}^{-j t} \\ = & \frac{1}{k} \cdot \sum_{t = 0}^{k - 1} \omega_{k}^{i t} \sum_{j = 0}^{k - 1} j \omega_{k}^{-j t} \\ = & \frac{1}{k} \cdot \sum_{t = 0}^{k - 1} \omega_{k}^{i t} \left( \frac{(k - 1) \omega_{k}^{-tk}}{ \omega_{k}^{-t} - 1} - \frac{\omega_{k}^{-tk} - \omega_{k}^{-t}}{( \omega_{k}^{-t} - 1) ^ 2} \right) \\ = & \frac{1}{k} \cdot \sum_{t = 0}^{k - 1} \frac{(k - 1) \omega_{k}^{t(i-k)}}{ \omega_{k}^{-t} - 1} - \frac{\omega_{k}^{t(i-k)} - \omega_{k}^{t(i-1)}}{( \omega_{k}^{-t} - 1) ^ 2} \end{aligned} $$ 就能把取模转为加法。 $\overset{\tiny\text{C}}{\footnotesize\textrm{差}}\overset{\tiny\text{C}}{\footnotesize\textrm{乘}}\overset{\tiny\text{B}}{\footnotesize\textrm{比}}$序列求和。 $$ \begin{aligned} S = & \sum_{i = 1}^n i x^i \\ x S = & \sum_{i = 2}^{n + 1} (i - 1) x^{i} \\ (x - 1) S = & n x^{n + 1} - x - \sum_{i = 2}^n x^{i} \\ (x - 1) S = & n x^{n + 1} - \sum_{i = 1}^n x^{i} \\ (x - 1) S = & n x^{n + 1} - \frac{x^{n + 1} - x}{x - 1} \\ S = & \frac{n x^{n + 1}}{x - 1} - \frac{x^{n + 1} - x}{(x - 1) ^ 2} \\ \end{aligned} $$ --- P5591。 $$ \begin{aligned} & \sum_{i = 0}^n \binom{n}{i} \cdot x^i \cdot (i \bmod k) \\ = & \sum_{i = 0}^n \binom{n}{i} x^i \frac{1}{k} \sum_{t = 0}^{k - 1} \omega_{k}^{i t} \sum_{j = 0}^{k - 1} j \omega_{k}^{-j t} \\ = & \frac{1}{k} \sum_{t = 0}^{k - 1} \left( \sum_{j = 0}^{k - 1} j \omega_{k}^{-j t} \right) \left( \sum_{i = 0}^n \binom{n}{i} x^i \omega_{k}^{i t} \right) \\ = & \frac{1}{k} \sum_{t = 0}^{k - 1} \left( \frac{(k - 1) \omega_{k}^{-tk}}{ \omega_{k}^{-t} - 1} - \frac{\omega_{k}^{-tk} - \omega_{k}^{-t}}{( \omega_{k}^{-t} - 1) ^ 2} \right) (x \omega_k^t + 1) ^ n \\ \end{aligned} $$ 其实直接 NTT 就做完了，因为 NTT 自带对 $k$ 的循环卷积。 --- 如果 $n$ 不是 $2$ 的若干次幂，考虑扩域做循环卷积。<https://www.luogu.com.cn/article/49olx91h>。分圆多项式。 https://www.luogu.com/article/4l2bmvkz --- 多项式推导。 扩域。 二次剩余。 Pollard-Rho。 ## Day 12（7.25）SG 函数 生成函数。 QOJ9631。 --- 博弈论。SG 函数。 --- 定义状态为$\overset{\tiny{\mathcal P\text{-position}}}{\footnotesize\textrm{必败状态}}$当且仅当其所有后继状态均为必胜状态或没有后继状态，否则为$\overset{\tiny{\mathcal N\text{-position}}}{\footnotesize\textrm{必胜状态}}$。 $\overset{\tiny\text{Sprague–Grundy theorem}}{\footnotesize\textrm{SG 定理}}$指出，任何$\overset{\tiny\text{impartial game}}{\footnotesize\textrm{公平组合游戏}}$的状态都与唯⼀确定的⼀个 Nim 游戏的状态等价。 定义两个状态的组合 $A + B$ 的意义是有两个独立状态 $A$ 和 $B$，每次可以选择 $A$ 或 $B$ 进行操作。 容易发现，必败状态组合必败状态为必败状态，必胜状态组合必败状态为必胜状态。 对于必胜状态组合必胜状态，先手不能把其中一个必胜状态转为必败状态，只能把其中一个必胜状态转为另一个必胜状态。后手同理。当必胜状态只能转为必败状态时，就得到了必胜状态组合必败状态。 所以我们发现，一个必胜状态的性质与其可以转化的次数有关。 定义一级状态为只能转化到必败状态的状态，二级状态可以转化到必败或一级状态。自然地，定义必败状态为零级状态。 也就是说，一个状态可以转为任意级别比它低的级别。 现在重新讨论两个状态组合的情况。如果两状态级别相同，先手如果提升其中一个状态的级别，后手一定可以改回去，否则先手降低其中一个状态的级别，后手可以在另一个状态对应操作，先手必败。否则两状态级别不同，先手把较高状态转为较低状态，先手必胜。 推广到更多状态的情况，发现是 Nim 游戏。 其实就是 $SG(S) = \underset{S \to T}{\operatorname{mex}} \{ SG(T) \}$，$SG(A + B) = SG(A) \oplus SG(B) $。 --- https://en.wikipedia.org/wiki/Sprague%E2%80%93Grundy_theorem https://zhuanlan.zhihu.com/p/20611132 ## Day 13（7.26）回滚莫队、莫队二次离线 字符串——wqs。 --- P1117。 有点神秘。 需要统计字符串中形如 $SS$ 的子串。 考虑枚举 $S$ 的长度为 $l$，再每 $l$ 个字符放一个断点，这样合法的 $SS$ 就会在连续的两个断点处出现，并形成两个断点的公共前缀和公共后缀。 道理在于，对于特殊形态的字符串，可以找到特殊的统计位置使得可行的字符串连续。比如回文串就在回文重点统计。 --- 回滚莫队。 左端点在同一块中时每次从块的右端点向左扩展到当前询问的左端点，再撤销回原状态，复杂度不变，但可以只用增加不用删除。 莫队二次离线。 莫队每次要求 $a_i$ 对 $[l, r]$ 的贡献，如果贡献能够差分可以考虑离线处理。 ## Day 14（7.27） 怀疑红牛买到假的了，除了让我一个上午去了十趟厕所没有任何效果，，， --- 这个 T2 也太好了。 首先，不妨设 $E(l, r)$ 为 $[l, r]$ 的节点到根节点的路径并。因为我们认为区间 LCA 深度不强于这个问题。 然后考虑如果每次求 $|E(l, r)|$ 怎么做。 发现莫队是容易的。但因为外面还有两层 $\sum$ 没什么拓展性。 为什么莫队是容易的。因为这个问题等价于一个区间数颜色。每条边的贡献只算一次。 所以使用扫描线，对于每条边维护最晚作为路径的时间。 那么如果查询左端点在 $[l_1, l_2]$，右端点为 $r$，就需要求 $\sum\limits_{i = l_1}^{l_2} \sum\limits_{j \in E} [a_j \ge i] = \sum\limits_{j \in E} \max(0, \min(l_2 - l_1 + 1, a_j - l_1 + 1))$。 然后右端点在 $[r_1, r_2]$，做一个差分，线段树做一个历史和。 --- 我在写什么。。。 --- 发零食和 KFC。这个成外也太好了。 --- 第二周比第一周过得快的原因是 jzy 在打 Hollow Knight。 --- 课件：<https://wxir.lanzouo.com/b00tbrup0j>。 密码是 11 位数字。 --- 再不来了。 # Week 52 ## 7.29 牛客多校。 ## 7.30 ## 7.31 # Weeeek 53 ## 8.20 补题。 https://ac.nowcoder.com/acm/contest/108305/B 交换序列中任意两个数，逆序对奇偶性必然变化。 https://ac.nowcoder.com/acm/contest/108304/A 旋转相当于 4 个四元环置换，逆序对奇偶性不变。 https://ac.nowcoder.com/acm/contest/108306/I 考虑交换两个值，两点在两棵树中的距离和仍然不变。 而如果已知距离矩阵，求最小生成树即为一个可行解。 ## 8.21 序列所有区间的不同 gcd 数量不超过 $n \log V$。 包含某个数的所有区间的不同 gcd 数量不超过 $\log^2 V$。 随机数据下只有 $\log V$ 级别，但类似 $\langle 2^a, 2^a \cdot 3 \cdots 2^a \cdot 3^b, 2^{a - 1} \cdot 3^b \cdots 3^b \rangle$ 可以卡得比较满。 考虑到每个数并不会在其所有因数处做贡献，只会在包含它的区间的 gcd 处做贡献。 ## 8.22 组队赛。 gym105887。 B 可以直接最大流。又因为有无穷边 $i + 1 \to i$，所以最小割必然是一个前缀划分为 S，后面划分为 T，可以枚举分界点。 E 有结论一段连续区间异或一个数会得到 $\mathcal O(\log V)$ 个连续区间。因为字典树的一个子树中的所有数异或后依然连续，而一个区间最多拆成 $\mathcal O(\log V)$ 个极大子树。 ## 8.23 UOJ919 环环相扣 对于两个数的情况 $a_i \bmod a_j + a_j \bmod a_i$，不妨设 $a_i > a_j$，就有 $a_j \le a_i \bmod a_j + a_j \le a_i$。如果 $a_i$ 没有取最大值，就一定不如 $a_i$ 取最大值、$a_j$ 取次大值更优。 推广得到三个数一定取最大和次大值。 设 $F([l, r], i)$ 为 $i$ 在 $[l, r]$ 内取得的最大值，发现可以由 $F([l, i], i)$ 和 $F([i, r], i)$ 合并，再特判两侧分别取最大值。而 $F([l, r], r)$ 可以由 $F([l + 1, r], r)$ 转移。 复杂度是对的。 --- UOJ751 神隐 对于树中相邻的两个点，当且仅当将其相连的边被选中时两点连通。 那么如果每条边在所有询问中被选中的次数相同且每次询问选中的边集不同，就只有相邻的点连通次数为每条边被选中的次数。 --- UOJ750 小火车 因为 $2^n \ge p$，根据鸽巢原理一定能找到两个和相等的子集得到可行解。 因为 meet in middle，查询和在范围内的子集数量是容易的，考虑二分。 # Week 54 ## 8.26 T4 考虑 set 维护扫描线。因为计算几何只会扫描线。 出两个问显然是因为 SPJ 比构造难，所以第二问比第一问简单。不难发现可以沿同一个方向出去。 如果两个区间有交，那就一定有一个区间的端点在另一个区间里。 P6802。 --- T3 是 1007，所以只能把人当作互相穿过，颜色就不好维护了。 但是不用维护颜色和人相关，因为每个人实际的相对位置不变，即颜色序列不变。 所以颜色可以由位置决定。 是好题。 --- T2 正解是 bitset，$\dfrac{2500^3}{32} = 4.8 \times 10^8$ 跑不满，1s 能过。乱搞也能过。乱搞被 hack 了。 --- 给一个排列排序可以做到 $\mathcal O(n)$。nodgd 说的。 ## 8.27 CEOI2025。 --- 极短 mex 区间最多 $2n$ 个，因为对于每个 $l$ 最多存在一个 $a_l > a_r$ 的极短 mex 区间，对于每个 $r$ 最多存在一个 $a_l < a_r$ 的极短 mex 区间。 然后一个极短区间可以扩展为极长区间。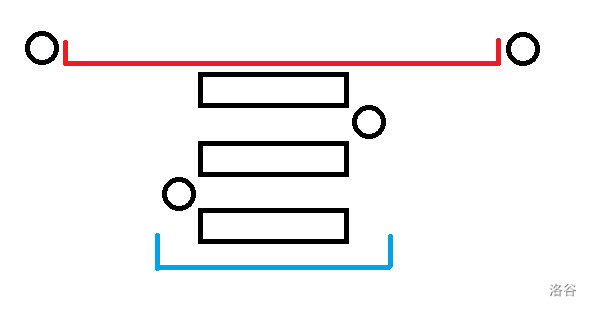 ![](https://cdn.luogu.com.cn/upload/image_hosting/k3dt6bt3.png) 如图，蓝色为极短区间，红色为极长区间。 ![](https://cdn.luogu.com.cn/upload/image_hosting/p55gxbmt.png "https://www.luogu.com.cn/article/n8ujc7v7") 又因为如果 $\operatorname{mex}(l, r - 1) = \operatorname{mex}(l + 1, r) = t$，$\operatorname{mex}(l, r) = t$，每个区域都形如阶梯状。 P4137，P9970，P10169。 --- mex 是最小的未出现的，也是最大的比它小的都出现的。 --- 有经验的选手可以一眼看出来是倍增。 直接倍增会把代价为 2 的操作拆开而无法转移。 $t + 2^i = (t - 1) + 2 + (2^i - 1) (t - 1) + 2^i = t + (2^i - 1)

就可以保证转移到花费为 2 的操作。

8.29

反射容斥。

Week 55

9.1

杂题。

9.4 集训队互测 #1

好题啊。

使用 chat.deepseek.com 通过 T1，再使用 yuantiji.ac 通过 T3，就有 200 分了。

以游戏为背景的题目经常出现的问题是打过的人比没打过的人更容易理解题意，这场比赛的 T1 就以一种巧妙的方式规避了这个问题。

出题人打 hollow knight 被抓了报复社会写的题面。

原来没有样例解释啊。

不如打 silk song。

P11331。

https://qoj.ac/problem/5356

0 分。

9.5

QOJ8527

注意到如果对于 i，要求 a_i - a_j = 2^k 是无法确定 k 的，但是要求 a_i + a_j = 2^k（a_i > a_j）是可以唯一确定的。所以考虑分治。

CF1819F

变换规则比较复杂，但是画成图就有了很直观的性质。看着像根据答案出题。

AT_arc163_d

首先，竞赛图缩点后的 dag 是一条链，且链上每对点都有从前往后的连边。

https://www.cnblogs.com/MoyouSayuki/p/18813125

9.6

T1 结论题想直接做，T2 搜索题想性质，T3 T4 没看。

枚举子集之类的前后两部分互不影响，考虑折半。AT_arc205_e。

AT_awtf2024_c。

Week 56

9.9

T1 数组开小了。

T3 考虑折半，进一步地，考虑分块。

T4 首先枚举终点再 LCT 维护基环树可以直接做。 发现如果终点在一段区间内，区间外的区间是确定的，考虑分块。进一步地，考虑分治。

9.13

比去年 NOIP 打得高，，，

T2 把区间左移看成把开头的数移动到到任意位置，发现最后被移动的一定是原序列的一段前缀。

比如原序列为 1, 2, 3\ |\ 4, 5，就是在 m 次操作中把前 3 个数插入到后面。这就要求后缀在最终序列中递增排列。

得到 DP 状态 $f_{i, j}$ 表示在大小为 $k$ 的前缀中进行 $i$ 次操作，移动了 $j$ 个数到后缀中，有 $f_{i, j} = f_{i - 1, j - 1} + f_{i - 1, j} \times (k - j)$，总方案数为 $f_{m, k}$。 集中注意力可以发现这其实就是斯特林数。注意力涣散可以发现这相当于求所有长度为 $m - k$ 的值域 $[0, k]$ 的非严格递增序列乘积之和。 求所有长度为 $i$ 的值域 $[1, j]$ 的非严格递增序列乘积之和。 考虑组合意义，有 $i$ 个球 $j$ 个盒子。没考虑出来。 问 deepseek。它说这个等于 $\displaystyle{i + j \brace j}$。说得也太好了。 因为 $\displaystyle{n \brace k} = \sum_{m_1 + \cdots + m_k = n - k} 1^{m_1} 2^{m_2} \cdots k^{m_k}$。考虑组合意义，斯特林递推时要么新开一个盒子，要么放到之前开了的盒子。枚举开第 $i$ 个到开第 $i + 1$ 个盒子之间的小球数量 $m_i$，有 $i^{m_i}$ 种放法。 也可以直接考虑斯特林数递推转移时的每条路径。 所以最后求斯特林一行上的区间和，推式子发现可以线性。 T3 发现操作顺序不影响结果，且结果唯一确定。考虑用线段树维护一段区间结果的形态。 # Week 57 军训。 ```text 团结就是力量 团结就是力量 这力量是铁这力量是钢 比铁还硬比钢还强 向着法西斯蒂开火 让一切不民主的制度死亡 向着太阳向着自由 向着新中国发出万丈光芒 ``` ```text 听吧 新征程号角吹响 强军目标召唤在前方 国要强 我们就要担当 战旗上写满铁血荣光 将士们听党⁢指挥 能打胜仗作风优良 不惧强敌敢较量 为祖国决胜疆场 ``` ## 初赛复习 linux 命令，g++ 命令，负数位运算，负数取模，主定理。 哈夫曼，格雷码，STL，class，后缀表达式。 # 初赛 这个题出得也太好了，复习的全都没用上，，， 忘记 $6^2 + 8^2 = 10^2$ 了。 # Week 58 ## 9.22 基本不等式 https://www.luogu.com.cn/article/jp5nzhsl https://www.luogu.com/article/9yptvqwo https://zhuanlan.zhihu.com/p/595224379 求导。 --- 轮换对称取相等是假的。只有齐次的时候可以用。 https://yummymath.github.io/多元微分/2020/03/20/007.math.html 不齐次的时候求的是其中一个驻点而不一定是最值点。 ## 9.22 博弈论 没有成外讲得好。 ## 9.23 集训队互测 #2 CF1740I。 赛时想法是差分后把每个环取出来，就是相邻位置一个 +1 一个 -1。考虑把偶数位置取反，得到两个子问题。看上去比较假，也不想写。 ## 9.24 CF1053（Div. 1） E 这种题有什么意义，，， --- 我错了，E1 有确定性做法。 首先有一个随机化，期望是 4n 的。过不去。剪枝可以过。 感觉上每次查询整个数组不优，考虑分治。 如果当前处理位置区间 $[l, r]$，维护在区间内出现的数中不在区间外出现和在区间外出现的数。 E2 考虑结合分治和随机化的做法。是垃圾题。所有交互题的 sub2 都是垃圾卡常题。 --- 假如我们有 $A_{n}$，求所有 $\sum B_i = S$ 的情况下 $\sum A_i B_i$ 的和。 这个是轮换对称的。所以可以设 $B_i$ 的期望为 $\dfrac{S}{n}$，答案就是 $\dfrac{S}{n} \sum A_i$。 # Week 59 ## 9.28 AGC073 题没补完，打不了。 ## 9.29 集训队互测 #3 在家玩原神，忘记参加了。 题出得好。 --- 不好。 ## 10.3 CF1055 这个 B 题简直就是智斗天花板，后面忘了。 其实是把横纵坐标分开看，发现往一个方向走更优且能够走到边界。 D 题首先每个数都至少有 $\lfloor \log a_i \rfloor$ 的次数，而且 +1 不会连续加在同一个位置。 F 题有经验的选手可以一眼看出来是倍增。 G 题考虑用更好维护的东西刻画这个形态。比如括号序。 # Week 60 ## 10.5 T2 假做法过大样例了。不要乱猜结论。 发现了增广路的本质是网络流反悔。 --- 毫秒随机种子。 ```cpp std::mt19937 rand(std::chrono::time_point_cast<std::chrono::milliseconds>(std::chrono::system_clock::now()).time_since_epoch().count()); ``` --- T3 对输入取模，大概率不是生成函数或者推式子，所以是 DP。 --- T4 求操作次数最少时的方案数，考虑把操作看成每次删一行或一列，发现每次删行还是列是确定的，把每次连续删若干行或列看成一个阶段，每个数在哪个阶段被删当然也是确定的。 然后观察。 矩阵有解的充要条件是不包含 $\begin{matrix}1 & 0 \\ 0 & 1\end{matrix}$ 和 $\begin{matrix}0 & 1 \\ 1 & 0\end{matrix}$，所以交换行列后可以形成一个阶梯型。 原矩阵无解就必然要改一个 $\begin{matrix}1 & 0 \\ 0 & 1\end{matrix}$ 中的至少一个，枚举后暴力求。 ## 10.7 T1 题目里有构造，考虑猜一个下界再构造答案。 T2 不好 DP，因为有折返，考虑最短路。 T4 首先发现选的一段 x 上的区间端点上一定取到 y 上的最值不然不优，这样限制后在 y 不交的情况下是可以保证 x 不交的。 可并堆。比如斜堆。 ## 10.8 T2 猜错结论了。不要乱猜结论。 T4 直接 DP，比如设 $f_{i, j, t1, t2}$ 表示前 $i$ 个点连了 $j$ 条边，直径不超过 $t1$，到 $i$ 的最远距离不超过 $t2$ 是否可行。做不了，因为值域不能设到状态里。但是最大最小，可以考虑二分一个值限制转移，DP 一个值。 本质一点，$f_i(j)$ 表示是否存在 $j$ 这个状态，但是一般只关心存在的最优的 $j$，所以设 $f_i = j$。计数题要记 $f_i(j)$ 的数量。所以最优化问题的本质是判定性问题。 不是凸的。不要乱猜结论。 平面上矩形赋值然后矩形求和。论文题。 ## 10.9 离线求区间内等于某个数的个数，不离散化可以线性。 --- T1 统计大小和恰为 $\dfrac{n}{2}$ 的不交无根子树对，要求线性。应该可以直接做，但是比较难写，写一半放弃了。既然 $\dfrac{n}{2}$，不难考虑以重心为根，形态就比较好，很多 cases 就不存在了。 T2 比较神秘，因为我并不会这个比较经典的问题，但既然答案这么问那就只能区间 DP 模拟题意然后四边形不等式优化到平方。 所求答案和子问题的区别在于，一个大区间被划为两个小区间，一个完全包含大区间的询问区间不会被下放。如果下放了会在第一层就处理掉，所以下一层的访问次数不能直接用，需要特判。 然而这种情况小样例没有，大样例没法调，T1 写了很久没时间了，就没有注意到。 arc164_e。做过原题就做不出来。 原题的 $n \log n$ 做法考虑一个询问区间会把序列分为三个部分，将没有被划分的连续段合并，为了先让深度最小，线段树形如一个满二叉树下方挂了若干对兄弟节点，访问次数为在两点中间的划分个数。就是 P1484。 T3 有 Prüfer 序推论。设目前有 $m$ 个连通块，大小分别为 $a_1, a_2, \dots , a_m$，则在连通块之间连边最后形成一棵树的方案数为 $\displaystyle \prod_{i=1}^m a_i \left(\sum_{i=1}^m a_i\right)^{m-2}$。 证明：https://oi-wiki.org/graph/prufer/#图连通方案数 T4 从小到大加边，先 $(n - 1)!$ 钦定树边的相对顺序，每条非树边需要在链上最后加入的点之后加入。因为不要和自己过不去，所以考虑倒着加边。 然后每个 $T$ 会对 $S \cap T \neq \varnothing$ 的 $S$ 产生 $+1$ 贡献，也就是会对 $S \subseteq \complement T$ 的 $S$ 产生 $-1$ 贡献，做一个高维前缀和。 ## 10.10 AT_arc122_e。 考虑倒序直接构造，可以放的数不会不能放了。 $ \gcd( x, \operatorname{lcm} \{S\} ) = \operatorname{lcm} \{ \gcd(x, s) ~\vert~ s \in S \}

AT_abc230_g。

\sum\limits_{i = 1}^n d^2(i) = \mathcal O(n \log^3 n)

CF1656H。

https://www.luogu.com.cn/article/4hl57kg2

https://qoj.ac/contest/1716/problem/56

这个 Div2 的 E 题也太坏了。F 是好题。

出现次数为奇数的数值之和，考虑给奇数位置乘 +1，偶数位置乘 -1。

10.11

T1 贪心，贪了两个小时，复刻 NOIP2024。

不要在模拟赛前一天晚上打 CF。

T4 轮廓线 DP。

求每种情况下方案数的平方和，考虑组合意义，等价于两个方案组合的方案数。

T3 这个 k 大直接二分意义不大。不考虑二分了。[l, r] 可以拆成 \mathcal O(\log V) 个子树，然后就相当于求一个子树无限制异或的 k 大最小。可以预处理，因为每个子树中叶子数量和是 \mathcal O(n \log V) 的。如果求的是小于等于 x 最多就不好预处理。

所以求小于等于 x 最多可能要二分成 k 大最小，一共双 \log。

Week 61

一三五杂题，二四六模拟。

10.13

这个 CF 也太难了，幸好没打，不然掉蓝了。

https://qoj.ac/blog/jiangly/blog/1420

构造恰为 k 的，考虑构造一个下界，一个上界，再进行调整。

最小化一个最大值，把最大值对偶成最小值，就是最小化最小值。

杨表。rsk 算法。

嵌套集是一棵树。

单位根反演。

P3206。动态最小生成树。线段树分治。

https://www.luogu.com.cn/article/zxqeaowk

这里面，是否：问题的核心在于保证递归到一个节点时候的有效点/边数量？ 我想说，这个算法并不容易归结为最基本的mst方法和线段树分治的简单结合，而是有一点它自己的东西。它的牛逼之处在于对于复杂度的保证。 而这一点，是否有推广？或者说，就可以把它当作一道孤题，不再细究？

10.14

T1 操作可逆，所以所有字符串构成若干等价类。考虑两个字符串可以互相转换的条件。再考虑连续进行的操作。

T3 首先嘴角一歪，小手一抖，有惊人结论 10!>c。所以只有最后 10 个数会进行排列。

由数据范围得到复杂度支持 \mathcal O(n k^2 + m k^3)，也就是预处理后每次询问枚举三个值计算其分别在前 c 个排列和子串中按顺序出现的次数。

这种构思就是思维偏短的代码题，过于炸裂，比较难写，虽然也能拿到一定分，是可接受的，若常数不算大就可以离 deadline 只有一天通过。

T4 二维是好构造的，因为可以直接对称。没有拓展性。

因为可以交换同一维中的切片顺序，所以可以让对应切片的颜色集合相同。也就是第 t 次会切出 x = t、y = t、z = t 三个切片，而对于一个位置 (i, j, k)，会在第 i 次、第 j 次、第 k 次被切到。第 i 次要求在 y = i 和 z = i 的切片中都有与其颜色相同的位置。第 j 次、第 k 次同理。

可以构造 (i, j, k) 与 (j, k, i)、(k, i, j) 颜色相同满足条件。特别的，比如 (i, i, k)，只要求有 z = i、x = k、y = k，可以只与 (k, i, i) 颜色相同。其实就是对每种数值轮换。

构造的正确性在于，要求颜色数量最多，就是对于每个格子要求和它颜色相同的格子数量最少。

这种构造方案的颜色数为 \displaystyle \sum_{i = 1}^K {K \brace i} \binom{N}{i} (i - 1)!。因为 K 维坐标有 i 个不同的数的方案为 \displaystyle {K \brace i} \binom{N}{i} i!，每 i 个形成轮换。

考虑把 N 作为参数差分掉。

\begin{aligned} f(n) = & \sum_{i = 1}^K {K \brace i} \binom{n}{i} (i - 1)! \\ = & \sum_{i = 1}^K {K \brace i} \left( \binom{n - 1}{i - 1} + \binom{n - 1}{i} \right) (i - 1)! \\ f(n) - f(n - 1) = & \sum_{i = 1}^K {K \brace i} \binom{n - 1}{i - 1} (i - 1)! \\ = & \sum_{i = 1}^K {K \brace i} (n - 1)^{\underline{i - 1}} \\ = & \frac{1}{n} \sum_{i = 1}^K {K \brace i} n^{\underline{i}} \\ = & \frac{1}{n} \cdot n^{K} \\ = & n^{K - 1} \\ \end{aligned}

也就是说构造出的颜色数达到了 \sum_{i = 1}^K {K \brace i} \binom{N}{i} (i - 1)! = \sum_{i = 1}^N i^{K - 1} 的上界。构造的来源也是这个式子的组合意义。

反着更好推，因为可以直接用普通幂转下降幂就推完了。

然后这个式子可以用来求自然数幂和。

具体的，先 $k^2$ 算斯特林，组合数就每次加一个数进去约分。 好像有比较魔怔的做法单次 $\mathcal O(k \log k)$，但 lwc 说没有意义，就不管了。 ## 10.15 AT_arc121_e 数排列可以数它的逆排列。限制是包含关系，直接用乘法原理。 AT_arc184_d 这个结果是不好 DP 的，考虑 DP 其过程。为了使过程和结果双射，就要让每个能操作的点都操作完。 AT_arc145_d 考虑若干个每一位只有 01 的三进制数，其中的任意两个数相加都不会进位。 --- T1 按照题意来说重边应该只算一次。。。而且我还是不知道为什么大样例有 4e6 行。 T2 考虑如果给的是每个点到这个点的距离，就做完了。考虑结果。 T4 P6261。 ## 10.16 T2 是极小极大 mex 区间板子，但是忘记主席树维护每个前缀每个数最后出现位置可以静态在线单 log 求区间 mex 了。 T3 开 1e7 就相当于把所有自动机卡掉了，能用的只有 KMP、Manacher、Hash。直接 Hash 处理所有子串一般带 log 二分，或者 log(log) 高维前缀和，也不考虑了。 考虑一个合法答案，其翻转后形成一个回文串，这个回文串是全串的（不完整）周期。没有形成回文串的再判一下。 道理在于统计回文串一般在其回文中心处，合法的就是一段区间，可以用 Manacher 求。如果在其开头结尾就，不好。 Manacher。还写错了。 T4 数位 DP。数位 DP 也不会写。 ## 10.17 网络流。 最大权闭合子图和费用流可以有负权。 --- AT_abc347_g 切糕。四边形不等式。 考虑将值域 $[1, m]$ 的离散变量 $x_i$ 拆为 $m$ 条边连成的 $S \to x_{i, 0\sim m} \to T$ 的链。 连边 $x_{i, j - 1} \xrightarrow{c(i, j)} x_{i, j}$ 表示 $x_i = j$ 时的代价，连边 $x_{i, j - 1} \xleftarrow{\infin} x_{i, j}$ 使得一条链上一定恰好割一条边。 如果连边 $x_{i_1, j_1 - 1} \xrightarrow{f_{i_1,i_2}(j_1, j_2)} x_{i_2, j_2}$，则表示当 $x_{i_1} \ge j_1, x_{i_2} \le j_2$ 时有 $f_{i_1,i_2}(j_1, j_2)$ 的代价。钦定 $j_1 > j_2$，因为 S 在 T 前面。 这样 $x_{i_1} = j_1, x_{i_2} = j_2$（$j_1 > j_2$）时的代价 $g_{i_1,i_2}(j_1, j_2)$ 就是 $\sum\limits_{j_1 \ge k_1 > k_2 \ge j_2} f_{i_1,i_2}(k_1, k_2)$。 所以 $f(i + 1, i) = g(i + 1, i)$，$f(i, j) = g(i, j) - g(i - 1, j) - g(i, j + 1) + g(i - 1, j + 1)$。因为最小割中边权 $f \ge 0$，就要求代价函数为蒙日阵，即满足四边形不等式。 本题中 $f(i + 1, i) = 1$，$f(i, j) = (i - j)^2 - 2(i - j - 1)^2 + (i - j - 2)^2 = 2$。 --- 二分图模拟最小割。 $$ \begin{aligned} & \sum\limits_{i = 1}^n \min(a_i, k) \\ = & \sum\limits_{i = 1}^n \sum\limits_{j = 1}^{\infin} [\min(a_i, k) \ge j] \\ = & \sum\limits_{i = 1}^n \sum\limits_{j = 1}^{\infin} [a_i \ge j] \land [k \ge j] \\ = & \sum\limits_{i = 1}^n \sum\limits_{j = 1}^{k} [a_i \ge j] \\ = & \sum\limits_{j = 1}^k \sum\limits_{i = 1}^n [a_i \ge j] \\ \end{aligned} $$ 两个流取平均，$f(k) \ge \dfrac{f(k - 1) + f(k + 1)}{2}$，是凸的。 ## 10.18 T2 常数写大了。 T3。 再次被本质不同子序列单杀。。。 计数题枚举怎么转移可以写出来的前提是状态设的是对的。 考虑钦定每对子序列都在首次出现的位置被统计。 T4 原题。忘记了。因为连续两个 $\le \dfrac{x}{2}$ 的一定可以选，两个 $> \dfrac{x}{2}$ 的一定不能选，所以把全部 $\le \dfrac{x}{2}$ 都选了再加 $> \dfrac{x}{2}$ 一定不劣。 把二分套主席树改成主席树套二分就可以少一个 log。 https://www.cnblogs.com/mian28/p/19151427#5381524 --- 时刻保持专注。 在草稿本上记录所有思维过程。以防从头开始或遗漏细节。 考试时对时间的感受未必准确，请提醒自己注意观察电脑时间。感到时间过快是思维不集中的表现。 --- > 总的来说，思路有两类： > > 1. 从理论出发，问题中关键的研究对象/片段，以及对它们的认识/刻画/经典技巧。 > > 2. 从实例出发，问题的特例，特殊性质（部分分），打表等观察性质并尝试推广。 > 你不知道这个题到底是什么怎么知道别人会不会？ > 在写代码之前应该有算法流程的设计，并把优化放在写代码之后。 > > 过早的优化是万恶之源。 > 先想所有题（40-70分钟），对每个题想出一个有效算法（正解，或者暴力+性质），直到时间足够或者没进展了。 > > 先想所有的东西，再做（写、研究）所有的东西。不要把具体推导细节/写题的工作放在列出可能的灵感前面。 > > 定期（10分钟）检查自己是否卡住，如果一段时间没有任何进展和方法（例如只能盯代码找bug或者没有任何思路的思考），立刻切换。（例如去写本题/其它题暴力） > > 可以通过去卫生间吹风等方式尝试重启大脑。 # Week 62 ## 10.20 今天，猫猫死了。也许是昨天，我不知道。 ![](https://cdn.luogu.com.cn/upload/image_hosting/mqd0lk2s.png) ![](https://cdn.luogu.com.cn/upload/image_hosting/sisghbxj.png) --- No Mind To Think。 选择一个中位数后会选最小的数增加和比它大的最小的数减少，发现每次选择相同的中位数不劣。再发现中位数固定时答案关于长度是凸的，二分即可。 F1 不是 DP。hyx T1。计数题考虑能不能组合数直接做。 --- 基于比较的排序考虑每个 01 序列。 --- 组合数前缀和。djq 分治。 https://www.cnblogs.com/zkyJuruo/p/16995141.html https://www.luogu.com/article/261ttwej --- P10383。 ## 10.21 T1 考虑把欧氏距离放缩为曼哈顿距离，再用莫队近似，就可以直接做无修改。 平衡复杂度得到莫队块长取 $\left\lceil \dfrac{n}{\sqrt{q}} \right\rceil$ 时复杂度为 $(2 \sqrt{q} + 1) n$，可以构造证明其取到了渐进理论下界。 --- T2 分讨题。不难猜到非平凡情况下答案为 $2^{\lfloor \log_2 n \rfloor + 1} - 1$。构造使得 $2 \le k \le n - 3$ 就可以取到上界，剩下的判一下。判的时候发现有 corner case，再判一下。没有 corner case。 具体的，非平凡情况下，设 $B = \lfloor \log_2 n \rfloor$。 先选 $(2^B - 1, 2^B)$ 取到上界。 然后每次取 $(2k, 2k + 1)$。 这样最多剩 $1, 2^B - 2, 2^B + 1, n$ 四个数没有选。 如果现在异或和为 $1$，就再选一个 $1$；异或和为 $0$，就删 $2^B - 1$ 选 $1, 2^B - 2$。 corner cases。 $k = 1$，直接选 $n$。 $k = n - 2$，根据 $\bigoplus\limits_{i = 1}^n i$ 讨论一下。 $k = n - 1$，根据 $\bigoplus\limits_{i = 1}^n i$ 讨论一下。 $k = n$，直接选 $[1, n]$。 corner case of corner cases，$n + 1 = 2^{B + 1} - 1$。 自然数前缀异或和呈现长度为 4 的周期。 --- T3 非公平博弈。 理性分析，之后的话，怎么说呢，注意力不太够了，就是什么呢，有 poly 复杂度的做法，复制一份，注意到什么的时候，改一行，然后对拍，离正解越来越近，直到通过，这是一个比较好的方法，这种题对拍也比较重要，大概就是这样吧。 --- T4 传统题。因为有 $k$ 次方所以不好拆贡献，但又有 $k \in \{1, 2, 3\}$ 可以枚举三个点算贡献，做到 $\mathcal O(n ^ {2k - 1})$。 正解复杂度 $\mathcal O(n ^ 2 k ^ 2)$。比较诈骗。 因为之前一道最短路的 T2，发现合法的最短路距离和起点集合是双射的。考虑判定最短路距离合法。 对于每个非起点的点 $v$，都有 $\forall u \to v, dis_v \le dis_u + 1$ 且 $\exists u \to v, dis_v = dis_u + 1$。 把全局限制双射为 local 限制，就可以直接 DP。 经典的，和的 $k$ 次方之和就用 $0 \sim k$ 次方和进行二项式卷积。P5296。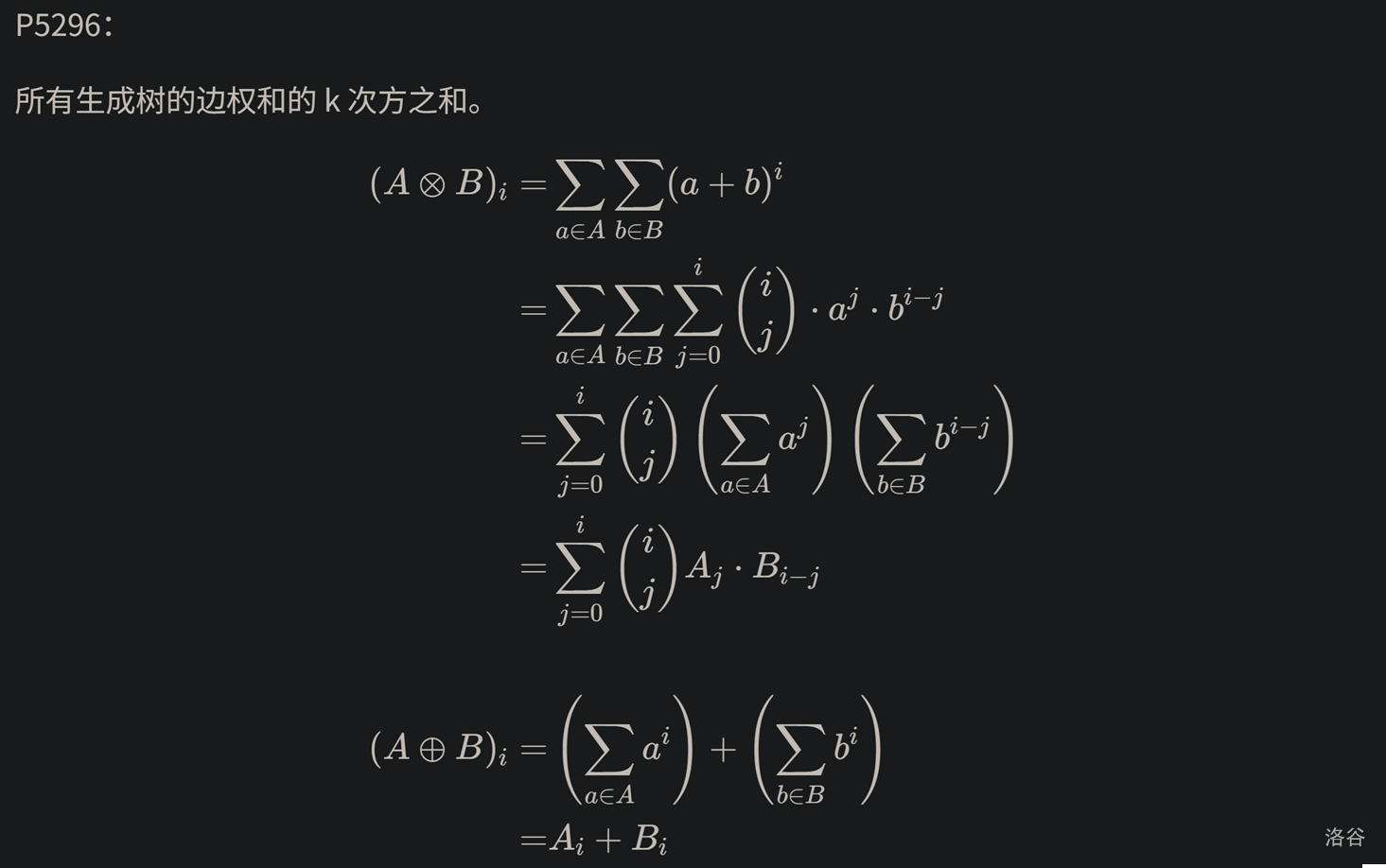 ![](https://cdn.luogu.com.cn/upload/image_hosting/mtxksuiz.png) ## 10.22 数学场。 实数域内多个数不取模相乘考虑转成对数相加。 有经典结论 $\gcd(F_i, F_j) = F_{\gcd(i, j)}$，忘记怎么证了。因为 $F_{i + j} = F_{i - 1} F_j + F_i F_{j + 1} = F_{i + 1} F_j + F_i F_{j - 1}$。 最后求斐波那契卷莫比乌斯前缀和，卷一个常数函数做杜教筛。有 $\sum\limits_{i = 1}^n F_{i} = F_{n + 2} - 1$。 杜教筛要预处理。复杂度 $\mathcal O(n ^ \frac{2}{3})$。 区间加，区间求 gcd。差分一下。 快速离散对数。P11175。loj6542。 概率期望题的本质是计数题。是 9 级知识点。 考虑当根据定义当计数题好做还是直接用期望线性性好做。 min-max 容斥。赛上考虑了一个小时没考虑出来放弃了。 不会期望。 期望的线性性质不要求各个随机变量相互独立。 一个 DAG，一个初始状态一些结束状态，求游走步数期望。经过边数期望等于每条边经过次数期望之和，而一条边只经过一次，就是每条边经过概率之和。示性函数。 $\displaystyle \sum_{i = 1}^m \frac{\binom{m}{i}}{\binom{n}{i}} = \frac{m}{n - m + 1}$。 --- https://www.luogu.com.cn/discuss/1178052 ## 10.23 T1 感觉删除不好做，就考虑了一个线段树分治的双 log 做法。过不去。但是直接整体用线段树维护就可以做到单 log。 数据结构也不会。 T2 不是结论题。 $\sum_{i = 1}^n (x - a_i) ^ 2 = n x^2 + (\sum_{i = 1}^n - 2 a_i) x + (\sum_{i = 1}^n a_i^2)$ 当且仅当 $x = \frac{\sum a_i}{n}$ 时取最小值。luoyudong。yangjunjun。qiyaokun。meiyinqing。 所以一个图上要求每条边两端点权差的平方和最小，每个点点权就等于相邻点点权平均值。 然后模拟解方程就可以做到 $\mathcal O(q 2 ^ n)$。 维护 $2 \left( \sum_{i = 1}^{2^{n - 1} - 1} a_i^2 \right) + \left( \sum_{i = 2}^{2^{n} - 1} a_i^2 \right) - 2 \left( \sum_{i = 2}^{2^{n} - 1} a_i a_{i / 2} \right)$。不好维护。 再观察一下，发现每个子树里每条边的代价和的最小值可以表示为关于根节点的二次函数，维护一下。 单边递归线段树。 https://www.cnblogs.com/PinkRabbit/p/Segment-Tree-and-Prefix-Maximums.html 因为是前缀信息，而且每个点能够向后影响的是一段区间。 --- 斜二倍增。 https://www.luogu.com.cn/article/u81tks5o https://mp.weixin.qq.com/s/zAsqVdcurYRCL5_x-srGxw https://zhuanlan.zhihu.com/p/1948533594613094277 ## 10.24 范围修改查询问题——清华大学李欣隆。 很经典，但是没看懂。 一个区间修改区间查询的线段树，修改有结合律，只需要考虑相邻区间信息的合并，区间信息经过一次修改的信息，相邻两次修改的合并。 特别的，单点修改全局/区间查询的线段树可以维护更好的东西。 --- 一般在比赛中能遇到的数据结构题还是找可以**贡献**答案的**结构**的**性质**，再用一些可以**维护**的**指标**来**刻画**其**形态**。 --- CF1942F。一年半之前看到的题，现在还是不会做。 ## 10.25 一中 2025 重庆市友谊赛 这个 T2 出得也太好了。 不要乱猜结论。 先考虑多项式复杂度的暴力 DP。 在一个第 $i$ 层有 $Fib(i)$ 个节点的树状物上选若干个点，不能有祖先关系，使得加权深度和最小。 CF2068D。 T3 是 P11340 状物。是集合哈希状物。是 `管乐部的练习时间快到了，你也尽快离开较为妥当哦。` 状物。 单调栈不好带修，换做法。最大值，考虑笛卡尔树。 CDQ 分治优化 1D/1D 动态规划的转移。 CDQ 分治以一个 log 将两个维度上的偏序合并为一个维度。时间或下标也是一维偏序。 每次把一个改为 1，只会影响以其为最大值的区间的转移，考虑差分计算答案增量。 # Week 63 ## 10.27 at_agc074_b。 考虑不变量，发现 $\sum a_i$ 和 $\sum i a_i$ 不变。 考虑构造。考虑平凡情况交换 01 和 10，相当于把一个 1 往左移，一个 1 往右移。 qoj14419。 考虑一个 $k, k - 1, \dots 1, 0, 0, 1, \dots k - 1, k$ 的反射容斥。 --- 反射容斥。 求从 $(0, 0)$ 走到 $(n, m)$ 的方案数，且路径不经过直线 $y = x + a$，$y = x + b$（$a < 0 < b$）。 反射了 $i$ 次的点容斥系数是 $(-1)^i$。 因为二项式反演。根本就不是二项式反演。lwc 在乱说。 > 你知道为什么容斥系数是 −1、1、−1、1 吗？ > > —— Just_int_mian 设一次经过 $y = x + a$ 为 A，经过 $y = x + b$ 为 B，连续多次经过算一次，答案就是 $\dbinom{n + m}{n}$ 减 A 开头的方案数和 B 开头的方案数。 而 A 开头的方案数等于经过 A 的方案数减去 B 开头且经过 A 的方案数。 B 开头且经过 A 的方案数等于经过 B 再经过 A 的方案数减去 A 开头且经过 B 再经过 A 的方案数。 反复容斥，直到方案数为 0 没有贡献为止。 因为卡特兰数，计算经过某条直线并到达某个点的方案数是容易的。 暴力枚举复杂度为 $\mathcal O\left(\frac{n + m}{b - a}\right)$。根号分治。 --- 保序回归。https://www.luogu.com/article/ul0uw9qz ## 10.28 笑点解析： > 第一行一个整数 n。 > > 求最大代价减收益。 > > 一行一个整数，表示答案。 --- 这个 T1 也太难了。 因为行列都可以任意交换，考虑把 a 和 b 排序。 然后每个 L 形的限制相同且互不影响，容斥即可。 --- T2 题面写的是错的，然后我又看错题了，所以没看出来题面是错的也不知道看错题了。还没有样例解释。 经典的，对于每个非起点的点 $v$，都有 $\forall u \to v, dis_v \le dis_u + 1$ 且 $\exists u \to v, dis_v = dis_u + 1$。因为 b 递增第二个不用管。 --- T3 min-max 容斥。and-or 容斥。 $\displaystyle \bigwedge_{x \in S} x = \bigoplus_{\substack{T \subseteq S \\ T \neq \varnothing}} \bigvee_{x \in T} x \displaystyle \bigvee_{x \in S} x = \bigoplus_{\substack{T \subseteq S \\ T \neq \varnothing}} \bigwedge_{x \in T} x

区间加，求区间按位与。

考虑线段树。

直接记答案相当于记每一位上是 0 还是 1，没法修改。

考虑到两个数模 2^{i + 1} 意义下如果相差了 2^{i}，在 i 位上与起来就一定为 0，且区间加任何数都与起来为 0。

也就是说，每个数模 2^{i + 1} 意义下都有一个长度为 2^{i} 的增量区间使得加上后这一位为 1。

发现在每一位上记加上 [l, r] 的值域后与起来为 1 就都可以做了！！！1

好题。

提供了一种基于修改的数据结构设计思路。比如维护区间加区间 0 数量就记区间最小值个数。

5e5 32 线段树 log 开 6s。

If the value of rhs is negative or is not less than the number of bits in lhs, the behavior is undefined.

For negative a, the behavior of a << b is undefined.

T4 状态有 0，00，1，赢了。

猫树。

建一个完全二叉树，发现两同层点的 lca 等于两点编号的二进制 lcp。即 lca(u, v) = u >> (std::__lg(u ^ v) + 1)。

baka's trick。

10.29

好题。

--- CF1148H。 区间版本区间和。 先考虑把区间版本差分为前缀版本，离线下来就是区间历史和，pvz 状物。在线就做持久化。 --- 预测 CSP：T1 神秘贪心，T2 树上最短路距离，T3 极小 mex 区间，T4 单侧递归线段树。 --- 这个杭电多校就会出结论题，没有任何意义。 --- upd：我错了，这个杭电多校出得也太好了。 --- $\color{red}{★}$ 表示巧妙但有点单薄的题。 $\color{blue}{★}$ 表示分析过程曲折复杂，且有启发的题。 $\color{purple}{★}$ 表示两者兼有，神仙题！ ♿ 表示 💩。 💀 表示只有 sans 能做出来的题。 🐱 表示只有猫猫能做出来的题。 ## 10.30 上午的当儿戏了没有打。 T3 统计树上路径，考虑点分换根 LCA。不好。限制是不经过有倍数关系的节点对，可以枚举，就是删掉一端点在某 dfn 区间，另一端点在某 dfn 区间的路径。 --- T1 ♿。 T2 ♿♿。 T3 ♿♿♿。 T4 ♿♿♿♿。 --- T3 好像是 $\mathcal O(n 2^{\omega(V)}\omega^2(V))$。因为 $\omega$ 很小所以都是常数。有的问题没法做的时候就细致分析暴力复杂度。 双指针状物考虑长度为 1 的区间可能不合法。 ## 10.31 试机。但是省选的时候试过机了，就没去。 # CSP$\tiny\text{——}\mathbb{C}\text{hongqing team }\mathbb{S}\text{election }\mathbb{P}\text{lus }2025

Day 1.0（11.1 a.m.）

在家玩原神，忘记参加了。

Day 1.5（11.1 p.m.）

题出的好，估分 100 + [64, 80] + [60, 100] + 20。

upd：100 + 80 + 75 + 8 + 无。

upd：T3 没判长度相等，挂成 0 分了。

现在 T3 估分是 \{0, 100\}。

upd：T3 AC 自动机写的 fail[0] = 1 挂 test2 了。

这个造数据的也太好了。

T1 \color{red}{★}。

T2 正解怎么真的是 1 秒 \mathcal O(2^k k n \alpha)，生气了。♿。

T3 \color{red}{★}。hash 字典树就 \color{blue}{★}。

T4 🐱。

先看了一遍题，发现 T1 随便做一下，T2 图论、T3 字符串、T4 计数都不太会。考场有点热。

T1 写完之后 T2 想了很久都没有低于暴力 \mathcal O(2 ^ k k n \log) 的做法，就看 T3。

T3 研究一下发现把 s1 s2 交替插成一个串就可以 AC 自动机直接做，就开始写，写了 2h，复杂度长度乘树剖和二分的 log，好像可能被卡常。

再写了 T2 的暴力之后看 T4，还剩半个小时，写状压，写完摆烂。

主要失误在于 T2 觉得不是正解就没有认真卡常，以及 T3 没看到 t 不保证长度相等，还有 T4 没研究原题。

后两个是运气问题。

T2 可以规约最小点覆盖，是 NPC。

全国统一评测时采用的机器配置为：Intel Core Ultra 9 285K CPU @ 3.70 GHz（关闭睿频与能效核），内存 96 GB。

贡献延后计算。

设 f_{i, j, k} 表示前 i 天，未录用 j 人，钦定了 k 个位置使得 c_x > j 但没有计算贡献。

如果第 i + 1 天这个人被录用了，j 不变，转移到 f_{i + 1, j, k + 1}。

如果第 i + 1 天这个人未被录用，j 加一。

当 c_{p_{i + 1}} \le j 时，枚举 t 个 c_x = j + 1 的位置及方案，转移到 f_{i + 1, j + 1, k - t}，转移系数为 \displaystyle (pre_{j} - (i - k)) \cdot \binom{k}{t} \cdot {cnt_{j + 1}}^{\underline{t}}。

否则，c_{p_{i + 1}} > j 且 s_i = 0，枚举 t 个 c_x = j + 1 的位置及方案，转移到 f_{i + 1, j + 1, k + 1 - t}，转移系数为 \displaystyle \binom{k + 1}{t} \cdot {cnt_{j + 1}}^{\underline{t}}。

算答案的时候就把还没有算贡献的再算一下。

这个的道理在于每个方案在转移过程中 j 是不降的，而每个 c_x = j 的贡献如果当前 j < c_x 没有算，就会恰好在 j = c_x - 1 \to j = c_x 的时候算到。

然后因为还要算 c_x \le j 的贡献，要记录的就是当前 \le j 的已经选了多少个。

https://www.luogu.com/article/xym8rh60

Week

11.3 集训队互测 #4

好题。

T1 🐱。

T2 🐱。

T3 💀。

T1 考虑看成每个人走完下一个再走。

KTT。

每次全局加，考虑离线下来。

CF1616G。

早知道就打零分了。

T2 放 *3500 是这个 👍

这种行为和好题推荐删边最短路有什么区别。

https://qoj.ac/problem/11252

11.4

$\displaystyle \sum_{i = 0}^n i^k \binom{n}{i}$ 同理，再枚举一下钦定的 $k$ 个中有多少个不同的位置，更自然地引入了斯特林数。 --- T2 推出来之后没意识到可以直接背包，又推了一些没有用的东西。 然后一直看 T3，因为没做出来过 T4。 T4 好像回滚莫队再平衡复杂度是单根号的。 --- T2 $\color{blue}{★}$。 T3 💀/🐱。 T4 💀。 --- 每次给一行或一列染色，每个点要么和所在行同色要么和所在列同色。 --- 图上每个点染 $1 \sim k$ 的颜色且一条边两端点颜色不同的方案数应该是 NP 的。已经有 $\mathcal O(n \oplus 3)$ 的确定性做法。lwc 说的。 因为我们只会求弦图染色。 弦图上任意长度大于 3 的环都有一个弦。大概就是形如三角剖分一样把一些三元环拼起来。 一个点是单纯点当且仅当与其相邻的点之间两两都有连边。 弦图的完美消除序列，使得从前往后删点，每个将要删去的点都是当前图的单纯点。 把完美消除序列倒过来加点，因为要求相邻点颜色不同，所以每个点的染色方案数都是当前确定的。 区间图一定是弦图。 --- 仔细考虑一下，发现均摊不能回滚。 > 直接把左端点可能造成影响的点也作为两个块之间的断点，这样的话，处理左端点移动的时候就等价于整块加，这部分只用 O(1) 打标记，没有任何块会被拆分成两部分。 💀💀💀。 块长不均匀的分块。 值域上分块后查最后一个大于等于 0 的位置，每一块维护最大值，从后往前遍历块，如果最大值大于等于 0，就在块内遍历。 --- 还可以普通莫队加二次分块，设小块块长为 $w$，大块有 $w$ 个小块，有单次修改 $\mathcal O(w)$，查询 $\mathcal O\left(\dfrac{n}{w^2} + w\right)$，总复杂度 $\mathcal O\left(\dfrac{n^2}{w^2} + n^{\frac{3}{2}}w \right) \ge \mathcal O\left(n^{\frac{5}{3}}\right)$，$w$ 取 $n^\frac{1}{6}$。 应该是要求修改能够差分，就可以对于大块整体打标记，查询的时候全部下放。 其实复杂度算出来和根号对数差不多，但是可以循环展开，可能会常数更小。 当内层 $k$ 次分块，块长 $w = n ^ \frac{1}{2k + 2}$。取 $k$ 为 $\log n$，$w$ 为 2，就得到一个线段树。 多层分块没什么用的主要原因就是不如直接写线段树。 ## 11.5 Testing Round 20 (Unrated, Communication Problems) B，考虑如果询问返回 $n - 1$，就可以确定区间内有 $1$ 和 $n$，二分出同时出现 $1$ 和 $n$ 的最短前缀或最短后缀，就可以得到 $1$ 和 $n$ 的位置，再用 1 个 bit 判一下哪个在前面。 C，考虑返回一个异或和为 0 的子集，就可以唯一确定改了什么。打表发现刚好够用。 如果通信题理论上做不了可以考虑 hash。 --- P12075。 考虑刻画，设点 $u$ 的顺序为 $p_u$，则删掉点 $v$ 的答案为 $\displaystyle \min_{u \not \in T_v} \left\{ p_u - \sum_{w \in T_v} [p_w < p_u] \right\}$。 类似线段树优化 1D/1D 的，直接把从每个 $v$ 转移的答案挂到数据结构上。 因为实际影响点 $u$ 决策的只有 $p_w$ 比它小的，所以按 $p$ 从小到大枚举。 树剖可以把链剖成 log 个区间，所以不在链上的也是 log 个区间。 ## 11.6 T3 是 `管乐部的练习时间快到了，你也尽快离开较为妥当哦。`。 发现没有强制在线，所以可以离散化。 --- T2 $\color{blue}{★}$。 T3 🎹。再有人出钢琴教室就再看一遍 MyGO。 T4 $\tiny{🐱}\scriptsize{🐱}\footnotesize{🐱}\small{🐱}\normalsize{🐱}\large{🐱}\Large{🐱}\LARGE{🐱}\huge{🐱}\Huge{🐱}\huge{🐱}\LARGE{🐱}\Large{🐱}\large{🐱}\normalsize{🐱}\small{🐱}\footnotesize{🐱}\scriptsize{🐱}\tiny{🐱}$。 凸猫。 --- 动态加删一维带权点，区间最值，考虑用 set 维护每个位置上的值，再用线段树维护，在线单 log。也可以把所有出现的点离线下来直接用线段树。 静态二维带权点，矩形最值，线段树套 vector。 --- 双指针找极小区间，每次确定左端点 check 当前区间右移一位是否合法，是假的，每个点会被尝试加多次。 每次确定右端点 check 当前区间不合法就移动左端点，是真的，因为当前区间是否合法可以维护。 --- CF2164。 C 是一个非常困难的贪心，简直比去年 noip T1 还难。 D 也非常困难，感觉现在做不出来去年 noip T1 了。 --- 神秘 C 题，题解写 5 个 lemma 证出来的。 CF 为什么没有大样例，，， --- 看了一下去年 noip T1，感觉赛上能以比较复杂的写法写完 T1 T2 并硬刚 T4 还是太有实力了。。。 ## 11.7 CF1893E。$\color{purple}{★}$。好题。 $1 \sim 3$ 轮换对称而且异或起来为 $0$。 首先，一条边两端点点权异或起来不等于 0 和边权，也就是不相同且边权等于其中一个。 然后，一个点相邻边边权异或起来不等于 0 和点权。 发现这些边权中等于点权的一定没有用。两个一样的异或等于 0 也没有用。两个不一样异或等于点权的也没有用。 所以要求每个点周围点中不等于其点权的边恰有奇数条。惊为天人。 最后就形成了两个独立的问题，先求染色方案数使得相邻点颜色不同，再求定向方案数使得指向每个点的边恰有奇数条。 先考虑一个经典问题，$n$ 元环 $k$ 染色方案数。 容斥，不难得到答案为 $k \cdot (k - 1)^{n - 1} - k \cdot (k - 1)^{n - 2} + \dots + (-1)^n \cdot k \cdot (k - 1) = (k - 1) ^ n + (-1) ^ n \cdot (k - 1)$。 然后第二个问题，首先有解当且仅当 $n \equiv m \pmod 2$。 如果一个点到其所有子节点的边方向已经确定，到其父节点的边就有且仅有一种定向方案。 同理，对于一个环可以根据其环长得到其总度数奇偶性，也可以确定到其父节点边方向。再确定环上一条边的方向，其它环边有且仅有一种定向方案。也就是环上翻转每条边方向不改变每个点的度数奇偶性。 因为整个图是有解的，所以根节点一定合法。 仙人掌上 DP，考虑每次加一条边或一个环。 --- CF1616G。$\colorbox{red}{\color{gold}{★★★★★}　　　　　}$ vs $\colorbox{blue}{\color{white}{☀️}}$。lwc 评的。 --- 最小树形图。有向边转为无向边。最小生成树。B 什么 ka。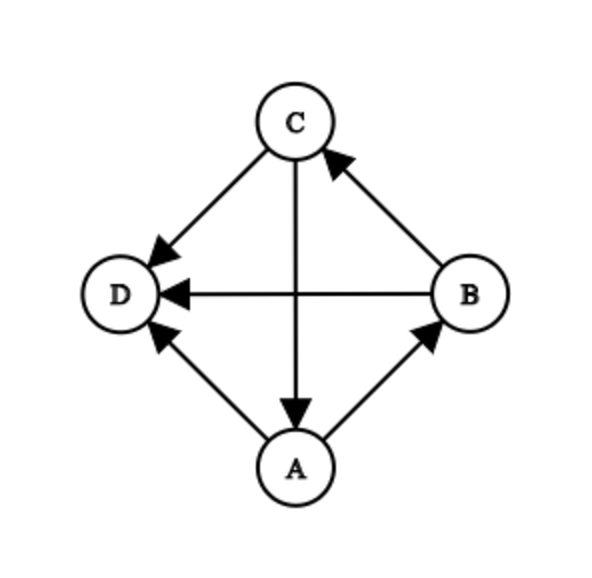 --- ![](https://cdn.luogu.com.cn/upload/vjudge_pic/CF1338E/145532c7db8128858a07ee6d5c9ef02bb615f7ae.png) 竞赛图没有如上子图，强连通情况下最短路不超过 3。 长度为 1 不用管，3 用总的减掉，考虑 2。 --- 发现 $m^2$ 可以做且 $m \sim n^2$，考虑不改变可达性的情况下删到只剩 $\mathcal O(n)$ 条边。 --- PA 评测机是 qoj 的 1/10。 并查集离线 RMQ。 移动右端点做扫描线，查左端点到根的最值，再路径压缩。不能按秩合并，小常数单 log。静态离线区间半群。 今天最重要的东西。 https://return20071007.blog.uoj.ac/blog/9292 为什么并查集路径压缩是单 log 的。 并查集优化建图。 --- P5811。很典。<https://www.luogu.com.cn/article/jayh6aob>。 $\Huge{🐱猫猫🐱}$。 双极定向。 --- 因为抽屉原理，生成树上加边成环，$m$ 是 $2n$ 级别。$n + \mathcal O(\sqrt{n})$。 每条边 $p$ 的概率删掉，$pm + \sum_{i = 3}^n (1 - p)^i \le pm + \dfrac{1}{p}$，取 $p = \dfrac{1}{\sqrt{m}}$。期望删这么多肯定有方法不超过它。 不该出现在这里。不是很好。 --- 很神奇，我也不知道为什么。 --- https://qoj.ac/download.php?type=solution&id=4898 综上，本题思维难度较高，代码难度适中，涉及了对最小生成树、辗转相除和整体二分等经典算法的深入挖掘，全面、有深度地考查了选手分析性质和实现算法的能力，是一道不可多得的好题。 https://qoj.ac/submission/440189 --- F 可以忽略，D 看情况。 ## 11.8 T1 是好题。 首先将题意转化为每次删 $k$ 个整数，就取消了时间维度上的限制，可以二分了。 T2 是套路题。有经验的选手。 T3 是 zzbbq 喜欢的题。 --- T1 其实是注意到在同一时刻对相同的维度进行多次操作是不优的。 --- T1 $\color{red}{★}$。 T3 ![](https://cdn.luogu.com.cn/upload/image_hosting/3t6gsazx.png) T4 🐱。 > 抑郁症数位 DP 题。 --- T4 好题。 设答案形式为 $\overline{a_1 a_2 \cdots b_2 b_1} \times c= \overline{b_1 b_2 \cdots a_2 a_1}$，不难发现 $c < k$，先枚举 $c$。 如果确定了 $i - 1$ 位向 $i$ 位的进位 $x$，再枚举 $b_i$，就可以得到 $a_i = (b_i \times c + x) \bmod k$。 然后注意到 $i$ 位到 $i - 1$ 的进位是可以求出来的。 因为 $i + 1$ 位向 $i$ 位的进位也可以求出来是 $y = (b_i - a_i \times c) \bmod k$，所以 $i$ 位向 $i - 1$ 的进位是 $\left\lfloor \dfrac{a_i \times c + y}{k} \right\rfloor$。 复杂度好像是 $\mathcal O(k^3 \log_k n)$。 在从两边往中间填的情况下确定当前填的数和 $n$ 的大小关系。分别记一下左边 $=$ 或 $<$，右边 $\le$ 或 $>$，从左边加数和右边加数都可以合并，最后再在统计答案的时候合并。 --- 四道都是原题。 P14562，P14563，P14564，P14565。 # Week 65 ## 11.10 这种题考虑构造出 2 的幂次拼起来。好像不行。 每个格子独立，用背包合并。 考虑构造一个尽可能大的答案，猜到大概形如路径上所有点翻转。 如果翻转这个 ```text RRRRRRRD DLLLLLLL RRRRRRRD DLLLLLLL RRRRRRRD DLLLLLLL RRRRRRRD DLLLLLLL ``` 答案只有 2800。 翻转这个 ```text RRRRRRRD DDLLLLLL DRRRRRRD DDLLLLLL DRRRRRRD DDLLLLLL DRRRRRRD DDLLLLLL ``` 答案有 2178111。 翻转这个 ```text RRRRRRRD DLLLLLLL DRRRRRRD DUDLLLLL DUDRRRRD DUDUDLLL DUDUDRRD RURURUDL ``` 答案得到了惊人的 14716400。 怎么回事呢。 --- case work。 A 取的一定是前缀。 贪心。 --- 广义串并联图拓扑序。 --- 交互题询问次数为 $k \log_k n$，考虑 $k$ 取 $3$。 --- 重叠的是一个回文串的 border。 回文串的 border 一定是回文串。 不重叠的不是很多。 border 是 log 个等差数列。回文串只有 1 个等差数列。对吗。这样吗。可能这里说的不太对。Runs。 --- qoj8049。 --- 支配对。 有 $n$ 个点，$n^2$ 个点对，每次查一个范围内的点对贡献最值。考虑只统计可能产生贡献的点对。 https://www.luogu.com/article/sy9wocs1 https://www.luogu.com.cn/article/rmdqa1b8 --- CF765F。 序列上 $q$ 次询问 $l, r$ 求 $\min\limits_{l \le i < j \le r}\{ |a_i - a_j| \}$。 贡献答案的一定是一个点对。 考虑在 $j$ 上统计所有 $a_i > a_j$ 的点对，比如有点对 $(i_1, j)$ 和 $(i_2, j)$，$i_1 < i_2 < j$。 因为 $(i_2, j)$ 不支配 $(i_1, j)$，有 $a_{i_1} < a_{i_2}$。 因为 $(i_1, i_2)$ 不支配 $(i_1, j)$，有 $a_{i_1} - a_j < a_{i_2} - a_{i_1}$。 不难发现对于每个 $j$ 只有 $\log V$ 个有贡献的 $i$，找出来二维数点即可。 --- https://www.codechef.com/problems/MINXORSEG 序列上 $q$ 次询问 $l, r$ 求 $\min\limits_{l \le i < j \le r}\{ a_i \oplus a_j \}$。 有点对 $(i_1, j)$ 和 $(i_2, j)$，$i_1 < i_2 < j$。 因为 $(i_2, j)$ 不支配 $(i_1, j)$，有 $\text{lcp}(i_1, j) \ge \text{lcp}(i_2, a_j)$。 不难发现如果 $\text{lcp}(i_1, j) = \text{lcp}(i_2, a_j)$，$(i_1, j)$ 就会被 $(i_1, i_2)$ 支配，所以 $\text{lcp}(i_1, j) > \text{lcp}(i_2, a_j)$，只有 $\log V$ 个。 二维数点即可。 --- P9058。 树上 $q$ 次询问 $l, r$ 求 $\min\limits_{l \le i < j \le r}\{ \text{dis}(i, j) \}$。 统计树上所有路径，比较好的结构是点分治。 点分治之后是 $\min\limits_{l \le i < j \le r}\{ \text{dis}_i + \text{dis}_j \}$。同一个分治子树内不用管因为不影响答案。 在 $\text{dis}$ 较大的位置统计答案，不难发现只用找比其小的上一个数和下一个数。 ## 11.11 T1 还是不说了吧。 T2 告诉你了还玩什么。 T3 你猜，猜对算你厉害。 T4 无特殊性质。 --- T3。 因为 jiangly，所以这种构造题一般考虑构造 2 的幂次相加。 而对于两个结构，可以把一个放左下角、一个放右上角实现相乘；长度相同的情况下，一个放左上角、一个放右下角实现相加。 或者说 DP 的转移是一个广义串并联图。 所以容易得到 $\mathcal O(\log^2 n)$ 的做法。 把共用的部分提出来，最后得到 $(k + 1) \cdot \lceil \log_k n \rceil$。当 $n < 10^{35}$，$k = 4$ 时取 $295$。 考虑混合进制，DP 得到 $4^{57} \times 5 \ge 10^{35}$，取 $291$。 不在最长上升子序列上的删掉，最后一个位置最大再删掉，就卡过去了。 为什么 $n < 10^{35}$ 我要写高精度？？？ --- $\Large\textrm{爆零了，下次记得测极限数据。}

如果这个 T3 不卡常，那么它在 NOIP 的构造题里应该是最好的。

T2。

推一下发现每个子树大小固定时其形态是固定的，且可以求出左右子树大小，就能递归计算了。

开 map 死的早，非递归就是好。

Disjoint Set Union on Tree。

继承重儿子信息，暴力加入轻儿子信息。

为什么要用这个呢，主要是背包加一个物品是 \mathcal O(m) 的，两个背包卷积是 \mathcal O(m ^ 2) 的。

at_abc311_h。

jiangly 说他的 ntt 2e7 两三秒就跑过了。

老板发表重要讲话，👏😭👏😭👏😭👈🤣👏😭👏😭。

T2 \color{blue}{★}。

T3 \color{red}{★}。

T4 🐱。

11.12

T1 ♿。

T2 ♿。

T3 💀。

T4 🐱。

\large\textrm{std::map 被卡常，考虑 std::unordered\_map 或手写。}

T3 口合集幂级数。

P11567

U488659

AT_agc061_e

T4 首先考虑把 +1 转为连续低位的一归零并向前一位进 1。

设 f_{j, u, s, t} 表示考虑低 j 位使用异或集合为 u，初始状态为 s，结束状态为 t。

以最后一次走的边作为点。 状态数 $\mathcal O(2^n \cdot \log V) $，每个有 $\mathcal O(2 ^ n)$ 种转移，有环，跑朴素 Dijkstra。 这个东西能够从低位到高位 DP 是反（我当前的）直觉的。 细致考虑整个过程。 从 $S$ 开始，异或一个子集，+1，异或一个子集，+1，异或一个子集，得到 $T$。 如果若干次 $+1$ 进位到最高位上，那么每次操作前后就是两个递归到低一位的子问题。 如果没有 $+1$ 进位到最高位上，那么最高位只与每个数异或次数的奇偶性有关。 --- > jiang 校长和托老师开黑是什么水平 > > jiangly：How to solve this problem? > > tourist：我不会说俄语。 ## 11.13 一中。8:30-13:00。 8:15 西门门口集合。 考号就是机号。 CQ-0054。 14:30。 戴口罩。大狗叫。叮咚鸡。 --- T1 $\color{blue}{★}$。 T2 $\color{blue}{★}$。 T3 ♿。 T4 💀。 到底是谁把这个 T1 放到 T1，然后 T3 放原题的？？？ 因为数学不好没考虑清楚 T1 调了很久，然后最后半个小时 T2 没写完。 通读全文但是不想题和随机顺序开题没有本质区别。尤其是这种 T3 过的比 T2 多，T2 过的比 T1 多（？）的神秘比赛。 P13046。 --- 仔细考虑一下，发现按照那个 P13691 倍增的做法第二问会算重。 P9140。同余最短路。 同余最短路是什么。想起来了。 如果是同余最长路好像就只能写转圈。$10^{11} \le V \le 10^{12}$。 为什么我先考虑矩阵快速幂再考虑倍增？ ![](https://cdn.luogu.com.cn/upload/image_hosting/l61a4lxi.png "一年前") 写的好。但是好像还要求 $\oplus$ 的交换律结合律。构成一个环。 线段树也要求分配律。 ## 11.14 贪心专练。 考虑贪心地考虑组合对象的性质。 当前有若干可以选的，为了给后面留尽量好的，当前贪心地选最差的。 --- CF2084F。 这个操作就相当于可以交换相邻两个数但要求前面比后面大。所以能够操作得到另一个排列的充要条件是，对于每个数，前面比它小的都在它前面，后面比它大的都在它后面。 所以贡献（影响？）答案的是每个点对。 两个出现的随便判一下。 一个出现一个没出现，出现的会使每个没出现的位置有一个区间的限制。位置（长度为一的区间）匹配区间。经典地贪一下，所有可以选的里选右端点最小肯定不劣。 如果都没出现。怎么办。观察一下，如果有 $pos_a < pos_b \land a < b$，就一定有 $l_a \le l_b \land r_a \le r_b$。所以一般都直接满足了，只有在 $r$ 相等时选最小的填。 --- P5290。 根据部分分，考虑根节点挂下来两条链。 不好。 考虑树形 DP，子树的根节点要单独开一个集合，每个子节点的集合可以合并。就有贪心的想法是按集合大小依次匹配。 感性理解一下正确性，两个子树，每个子树有若干集合，合并两个集合得到其最大值。所有集合里最大的集合肯定会保留，那就把它的另一个子树里最大的和他合并，肯定不劣。 而且这个合并类似长链剖分，反正每个只会被合并一次就删掉，用堆来维护是单 log。 --- qoj10404。 还是匹配。 两个区间可以匹配的充要条件是 $l_i + l_j \le s \le r_i + r_j$。 那么对于一个 $i$，某个 $j$ 可以与其匹配的条件就是 $l_j \le s - l_i \land r_j \ge s - r_i$。 还是匹配能匹配里最劣的。因为有全序可以两两比较。 --- at_agc045_b。 要求每个子串中 01 个数差绝对值的最大值最小。 不难想到把 01 改为 $\pm 1$ 画折线。 一个区间的值就是结尾和开头高度差。 考虑一下，发现，所有区间中开头结尾高度差最大的，一定是取到整个折线的极差。 要让整个折线极差最小。考虑枚举上界。 上界最小时，先将所有未确定位置取 $-1$。然后从前往后贪，不会使上界更大就调整为 $+1$。 将上界增加 2，下界最多增加 2。不优。 证明你去问一下 lwc。 所以只用考虑上界的最小值和最小值加一。 ## 11.15 T1 红色的星。 T2 轮椅。 T3 蓝色的星。 T4 猫。 --- T3 考虑一下，发现考虑之后就会归约到 LCT 维护笛卡尔树状物。考虑得不好。 怎么做呢。 $\mathcal O(n^2)$ 过 5e4。 --- 有点神秘。 就是说维护某个数可以作为最值的区间算贡献，一般是找到它前面最后一个 $\ge$ 它的、后面第一个 $>$ 它的。维护这个结构的变化量可以是 $\mathcal O(q n)$ 的，也不是很好优化。 发现给一个数加一会把所有最大值取到这个的区间答案 +1，然后你找前面最后一个 $>$ 它的、后面第一个 $>$ 它的就可以了。 +1 的时候就直接算的这个 +1 的贡献，而不是算这个 +1 对别的贡献的贡献。 你问一下 Just_int_mian。 --- 发现之前写线段树上二分的写法就是依托。 比如查 $[l, r]$ 内第一个 $\ge x$ 的数，$[l, r]$ 被拆成 $\mathcal O(\log)$ 个区间，递归的时候会从左往右遍历到，对于第一个 $\max \ge x$ 的区间再进行线段树上二分。 --- $\Large\textrm{T1 判了 k = 1 没判 a = 0 挂了。}

这个出题人不开 sub 也太好了。

为什么 Div 2 比 Div 1.5 难。

CF1456E。

今年 NOIP T4 绝对是数位 DP。

这个代价形如每一位上相邻两个数产生贡献，又因为二进制的上下界限制形如一段和上下界相等、一段和其中一个相等、一段没有限制，所以每一位上的贡献只和还有限制的有关，设 f_{i, l, r, sl, sr} 表示第 i 位上 l 的限制为 sl，r 的限制为 sr，中间任选的最小代价，转移的时候枚举一个断点。

在线莫队。

考虑一下，莫队的复杂度是每个点到上一个点的曼哈顿距离，所以我们先预处理一些点，然后每次询问从最近的点移动过去。

再考虑一下，发现这个东西等价于分块后预处理所有区间块的答案，然后每次询问在被完全包含的最大区间加点进去。

但是莫队还要存一些当前区间的信息。存不下。如果可以前缀相减得到，就很好。不然就要可持久化，感觉比较难写，也没什么用。

Week 66

11.17

这个 CF 也很难。

A 题发现把当前最小值合并到其旁边两个数中的较小值肯定不劣。

或者是你考虑把环断开后，得到 P4393。然后对于最大值肯定只会合并两次，左右分别合并，答案就是 \sum\limits_{i = 1}^n a_i([a_{i - 1} < a_i] + [a_{i + 1} \le a_i]) = \sum\limits_{i = 1}^{n - 1} \max(a_i, a_{i + 1})。

这个题也太好了。

B 题考虑对于结果判定其合法。猜一下。猜到是 \sum\limits_{x \in S} cnt_x \ge \max\limits_{x \not\in S} cnt_x。然后背包就做完了。

给这个条件与一个真命题，发现这个等价于 \sum\limits_{x \in S} cnt_x \ge \max cnt，直接做就做完了。

这个 C 题观察一下，每次给一个数 +1，如果给比较小的数加，相当于加到最大的数，然后给最大的数加。所以当前先给最大的加不劣。

然后就只会用到最大的 \mathcal O(\log V) 个数。

这个 D 题规约最小路径覆盖。

Sequence Covering Problems。

比较 \text{ab} < \text{ba}，考虑比较 \text{a}^{\infin}\text{b}^{\infin} < \text{b}^{\infin}\text{a}^{\infin}，然后就是比较 \text{a}^{\infin} < \text{b}^{\infin}。?

11.18

T2 \color{blue}{★}。

T3 🐱了个🐱。

T4 小猫，大猫，_{\Large🐱}^{\tiny{🐱🐱🐱}}神。🐱🐱为什么是神？首先是犯下傲慢之罪的 myq。

T2 既然这么问了就一定是区间 DP。

区间 DP 优化到 \mathcal O(n^2) 不一定只有四边形不等式，可能是只有 \mathcal O(1) 种转移。

T3 Just_int_mian 说这种题要考虑找中间状态。说得不好，因为这道题卡常。

考虑多种构造方式，然后根据 A 非零数量和 B 非零数量选最少的。

好像所有构造方式其实都考虑到了，但是最坏情况下都会达到 2n 甚至 3n 就没仔细想。

感觉一下，就是因为 \sum_{i = 1}^n a_i = n，就一定会形成零和非零的区别。

注意不存在一个子任务完全包含其他子任务。

喵了个喵怎么做。

T4 好像 k = 2 是好做的，但是没调出来。

\Large\textrm{调出来了，有个地方没取模。}

jiangly 说方案数可能取模等于 0，就没有逆元。

P14518。

cloudflare 炸了导致 luogu.com、luogu.me、codeforces、atcoder、loj、qoj、vjudge、bzoj 都打不开了。

以验题人心态看待比赛。——\mathbb H 之神

如果你问常数在 noi 真的有用吗，真实情况就是常数更小，就算复杂度不对也能冲过去。所以还是有必要的。——大 H

枚举啥呀。不会。——小 h

不要把比赛当儿戏。——\mathbb H 之神

真的菜就多练，别到处骂人——大 H

这周目前打了 1 场模拟赛，令人感慨。——小 h

11.19

T1 ♿♿♿♿。

T2 ♿♿♿♿。

T3 ♿♿♿♿。

T4 ♿♿♿♿。

T2 是 A000296。

T2 要求前 n 行每行斯特林数的和，即前 n 项 Bell 数。这个应该是做不了的。但是。

\begin{aligned} Ans & = \sum_{i = 0}^n \binom{n}{i} (-1)^{n - i} B(i) \\ B(i) & = \sum_{j=0}^i \sum_{k=0}^j \frac{(-1)^k(j-k)^i}{k!(j-k)!} \\ & = \sum_{k=0}^i \sum_{j=0}^{i-k} \frac{(-1)^k}{k!}\frac{j^i}{j!} \\ Ans &= \sum_{i = 0}^n \binom{n}{i} (-1)^{n - i} \sum_{k=0}^i \sum_{j=0}^{i-k} \frac{(-1)^k}{k!}\frac{j^i}{j!} \\ \end{aligned}

这个东西，你感觉一下，前面的 \sum_{i = 0}^n \binom{n}{i} (-1)^{n - i} 这个东西最好和与 i 相关的 j^i 放到一起提到后面搞一个二项式定理，但是与 i 相关的还有 j 和 k 的求和上界依赖 i，不好把 i 提到后面，又但是里面算的是个斯特林数，上界超出去是没有问题的，，，

\begin{aligned} Ans &= \sum_{j=0}^n \sum_{k=0}^{n - j} \sum_{i = 0}^n \binom{n}{i} (-1)^{n - i} \frac{j^i}{j!} \frac{(-1)^k}{k!} \\ &= \sum_{j=0}^n \frac{1}{j!} \sum_{k=0}^{n - j} \frac{(-1)^k}{k!} \sum_{i = 0}^n \binom{n}{i} (-1)^{n - i} j^i \\ &= \sum_{j=0}^n \frac{1}{j!} \sum_{k=0}^{n - j} \frac{(-1)^k}{k!} (j - 1)^n \\ &= \sum_{j=0}^n \frac{(j - 1)^n}{j!} \sum_{k=0}^{n - j} \frac{(-1)^k}{k!} \\ \end{aligned}

感觉和斯特林数相关的推式子比较玄学，可能是因为斯特林数的通项公式推导严重依赖于组合意味，，，而组合意味就是依托，，，

还有就是组合数学推导有一些结构可以直接消掉一个 \Sigma，比如经典的，二项式定理，朱世杰恒等式，之类的东西。

原来 \sum 的优先级比加法高。

非平凡的，总和等于乘积的，正整数集合，有且仅有 \{1, 2, 3\}。

因为 w(l, r - 1) + w(l + 1, r) \le w(l, r) + w(l + 1, r - 1)，所以 w(l, r) - w(l, r - 1) - w(l + 1, r) + w(l + 1, r - 1) \ge 0，即二维差分为正得到凸性。

因为 w(1, n) \le 2n，所以二维差分后只有 2n 个 +1，可以通过 \mathcal O(n \log n) 次询问得到矩阵。

然后就是一个正常的 DP 题，长度为 n 的序列，不超过 2n 个区间，将序列划分为恰 k 个连续段，包含一个就会使得代价 +1。

正常在哪。

把包含一个区间有代价改为包含分隔点的区间有贡献。

然后就是 AT_wtf22_day1_d。

这个东西。

等下我看一下题解。

线性规划对偶是什么。

反正就是你对偶一下，问题就转化为有 m 个区间，需要选取一个区间的集合 S，使得 m - |S| + k \cdot \max\limits_{i = 1}^n \sum\limits_{j \in S} [l_j \le p_i \le r_j] 最小。

每个点覆盖次数不超过 x 次，选尽可能多的区间。

这个应该是一个经典问题。有点眼熟。

，，，是 P3358。

然后就可以模拟费用流了！

首先 x = 1 是经典贪心，按右端点排序然后从左往右贪心选就行了。

然后考虑 x 增大，因为这个有决策单调性，原来选的继续选肯定不劣，就在这个基础上进行贪心，每次取右端点最小的合法区间加进去。或者考虑到费用流所以是对的。

但是根据费用流的做法，好像每次重新选不交区间就是对的。？不懂。

哦懂了，就是因为每个点最多被覆盖 x 次，所以所有选的区间一定可以划分为 x 层，费用流就可以反悔地选出来。

回滚背包。

11.20

看了一下 T1，应该是点分治随便做一下就行，不怎么好写，不管了。

看了一下 T2，直接线段树就行，空间回收的话应该是线性的。

看了一下 T3，就是说有若干个环，每次把一个环缩成点或者把一个环加到另一个环上。答案不是凸的。

看了一下 T4，如果设状态为到了第几个房间有多少块钱，最后一个房间肯定是尽可能选，是凸的，前面的房间就做一个卷积。反正是一个 slope trick 状物。

感觉 T2 比 T1 好写，就开始写 T2，写了 3h 写爆了，最后半个小时看 T1，发现不用点分治。

T2 因为这个可持久化只用最新版本，正解是重构 \log 次，然后时间复杂度不变，空间复杂度就是最大 \mathcal O(n) 的。

但是空间带 log 可以过，标记永久化就行。♿。

这个回收空间我调一百年都调不出来了，，，因为他这个，有两个点，在线段树上跳，一个回收之后另一个还要访问原来的，，，不调了。。。

仔细考虑一下 T3 的策略，应该是要么把最大的连成自环，然后把 2 \sim k 大的连过去；要么钦定最后选的，把其他的加上去。而且上文说的那个转化是错的。

第一种是好做的，做第二种时发现不同的环长只有最多 \sqrt{2n} 个，所以对每个连通块暴力求加到每种环长的最大值，每种环长再选最大值就行了。

T4 写凸优化 DP 会被卡常，考虑一些神秘的东西，瓶颈就在排序和二分了。

T1 \color{blue}{★}。

T2 ♿ * 128。

T3 \color{blue}{★}。

T4 🐱。

10.21

jiangly 讲矩阵树。

不考虑环是 \prod out，然后把环容斥掉。

\sum\limits_{选出边} \sum\limits_{环的子集 S} (-1)^{|S|} \sum\limits_{一些环} (-1)^{|S|} \prod\limits_{不在环上的点 v} out_v

讲得好。

AT_abc323_g。Ax + B 状物行列式。先消常数项，再消一次项，有两个对角线，DP 一下。

线性递推。BM 算法。

带状高消。

做点 NOIP 题。

P9120。

好题。\color{purple}{★}。

可以轮换每一列，要求每一行极差最大值最小。考虑二分。

因为极差，考虑枚举最大值。发现不用枚举，全局最大值肯定也是单行最大值。

找出全局最大值和全局最小值。不妨设两者不在同一列或同一行。

然后就可以做 k = 2 了，因为每一列都是独立的，直接选就行。

拓展到 k = 4，只有后两行会互相影响，就得到一个二维数点状物，数一下就可以了。

P8868。

考虑并不存在的 b = 1 的部分分，发现这个题严格强于每次给一个区间，求其所有子区间的最值和（P10637）。这个也很困难。

考虑最值的形态，每个点会在一个（一个点顶到对角线的）矩形（互不相交）里做贡献。

离线下来扫描线。每个点对应一次区间赋值和一次区间撤销。因为求和，所以是区间加和区间减。

查询的就是一个矩形和，差分一下，就是区间前缀和，PVZ 一下。

那么这道题怎么做呢。

这道题就应该是 a 区间加，b 区间加，\sum a \cdot b 历史和。了。

11.22

本题没有附加文件最牛刷题者嘟嘟嘟哒哒哒度与好。

T1 钦定可以到哪些点，组合算一下就可以了。

T2 发现这个是一个凸包，扫描线 DP 算一下就可以了。

T3 比较有意思。

考虑先二分答案，然后树上有一些关键点，先手要在后手到达任一关键点前将其置零。

然后如果根节点的子节点中有至少两个关键点就死了。

仔细考虑一下，这个就是说如果走到一个点，这个点的子节点有 k \ge 2 个关键点，就死了，等价于这个点是关键点且要被多消 k - 1 次。

就可以算出有没有关键点被推到根节点。

再考虑一下，这个相当于每个关键点从其父节点往上推到第一个非关键点处消掉，就不用二分了，wrb 并查集做一下就是线性的。

wrb 并查集为什么是线性的。

题解做法应该是基于 http://oj.daimayuan.top/contest/389/problem/3340 的。

代码源卡常是不是从来没有成功过。

T4 考虑这个转移，先 f_i(j) = f_{ls}(j) + f_{rs}(j) + w(i, j)，然后 f_i(j) \gets \min \{ f_i(k) \} + 1，所以极差不超过 1，维护差分数组启发式合并。

主要因为这个东西是对应位置相加而不是做卷积，就很好，连续段数量就是相加而不是相乘。

T1 \color{blue}★

T2 \color{blue}★

T3 \color{red}★

T4 🐱

11.23

17:35 CF。

E 题，因为我们打了集训队互测不知道 # 几，反正发现可以把每一种数分开看，前一个数走完后一个再走，再对每一种数的答案取最大值。

这个 F 题赛上开摆了没有想，赛后发现好像是比较平凡的。

考虑其结果是一个以 n 为根的根向树，代价就是 1000 \cdot \max dep + \sum (fa_i - i)。

用一个树状数组状物，就是 1000 \log n + \dfrac{1}{2} n \log n，不够好。

考虑三进制树状物。考虑 \sqrt[3]{n} 进制。这不是三层分块吗。

Week 67

11.24

这个 E 题。首先横纵坐标是独立的。然后就是说，你关注，这个整体，所有坐标和，的变化量，发现中间都抵消了，只有第一个点到最后一个点的变化量，而整体变化量又可以求出来。

jiangly 讲的，考虑找不变量，设当前激活点为 s，势能函数 \Phi = \sum\limits_{i \neq s} p_i + k \cdot p_s，即设激活点的倍率是其他点的 k 倍，要求势能函数作为不变量操作前后相等。

可以解出 k = -1。但是为什么可以假定不变量是关于每个点位置的线性组合？不懂。

老板：

继续做 NOIP。

P5023。

观察。打表。观察出必要条件一个 1 左下方必须是 1。好像没什么用。考虑直接 DP。好像 DP 不了。

再观察一下，发现极小不合法结构大概形如

····
···1
····
·0··
····
····
···0
··1·
·x··
···0
····
·1··

反正就是大小不超过 3。

有点麻了，看题解。

♿题，使用比较优的方式打表，然后注意到递推式 f_{n, m} = 3 f_{n, m - 1}，就可以直接算了。n \le 8 好像并没有什么用。浪费我一个晚自习。

再也不想做 19 年之前的 NOIP 了。

11.25

完全二分图生成基环树计数。

感觉是 prufer 序。但是我连二分图生成树怎么证都不知道。

神秘比赛过前两题一百个人，后两题加起来过一个人。

T1 完全图生成树定向。

先确定上界 \dfrac{n(n-1)}{2}，下界 n - 1。

不妨假设定向得到的是叶向树，然后点对数就是每个点子树大小减一之和。

显然下界到上界都可以得到。 --- T2 博弈论板子。 --- 我错了，T3 是生成函数。而且 prufer 序是超纲知识。 --- 做 CSP-S。 P5665。 好难啊。想了一百年只会 $\mathcal O(n ^ 2)$ 做法。设 $f_{l, r}$ 为最后一段是 $[l, r]$ 的最小代价，$l$ 相同的双指针转移。 发现最后一个区间在能够合法的情况下左端点往右移肯定不劣。 不管了，看题解。 设 $g_i$ 表示以 $i$ 结尾的区间的最后一个合法转移点。 然后就直接 $g_i = \max\{ j ~\vert~ s_i - s_j \ge s_j - s_{g_j} \} $，单调队列求一下。 这个东西的道理在于什么呢。 最后一个区间在能够合法的情况下左端点往右移不仅对于它往前的不劣，也对于它往后的不劣。 或者说你算一个的时候前面已经取到尽可能后面了，再往后取就不合法了。 --- wxir 说今年要考笛卡尔树。 AT_agc028_b。 --- CF117C。 云程发轫小队大战黄题。 　**Just_int_mian**。很强。 你先找一个环，然后对于两个间隔为 2 的点，如果它们不构成三元环就可以把环变小。 也就证明了竞赛图存在环就一定存在三元环。 --- AT_arc159_b。 ## 11.26 T2 用期望线性性拆成每个点权值乘概率和。 T3 感觉是大分讨。 T4 2e5 两秒 2G，正解单 log，根号 log 可以过。 --- $\Large\textrm{数组开小了，下次记得测极限数据。}

T4。

图上动态修改点的颜色，求异色点最短距离。

首先发现最短距离肯定是一条边。

然后使用各种分治就可以做到根号带零个或若干个 log。

如果在图上做应该都要带根号。考虑在树上做。

不妨猜测只有最小生成树上的边有用。

如果有一条边不在最小生成树上且两端点异色，则其在生成树上构成的环中其余任意边都不会比它边权大，且一定会有两端点异色的边。

树上和图上的本质区别在于什么呢，就是说你原来对每个点要维护其邻域上的答案，单点修改也会贡献到其邻域所有点；现在对每个点维护其子节点上的答案，单点修改就只会贡献到其父节点。

或者说你给无向图定向，每个点沿方向贡献，改一个点的复杂度就是这个点的出度，然后你从度数小的指向度数大的，每个点出度就是 \mathcal O(\sqrt{m}) 的。假设无重边。这个应该是渐进意义下最优的，因为直接放一个点数 \mathcal O(\sqrt{m}) 的完全图作为子图肯定可以卡满。

T3 直接做一般要对每种可能的答案形态大力分讨，包括左端点在哪个串，右端点在哪个串，对称点在哪个串里面之类。但是你把三个串拼到一起搞一个区间 DP 就要好一点，就可以从转移的角度进行优化。

怎么又是三道图论。

下次要带耳塞了。

bzoj2448。

好题。很深刻。

直接 DP 是 f_{l, r} = \min\limits_{l \le k \le r}\{ \max(f_{l, k - 1}, f_{k + 1, r}) + a_k \}。

里面这个 \max 不好。观察到 f_{l, k - 1} 关于 k 递增，f_{k + 1, r} 关于 k 递减，所以两者存在交点 g_{l, r} 使得 f_{l, r} = \min( \min\limits_{l \le k \le g_{l, r}}\{ f_{k + 1, r} + a_k \}, \min\limits_{g_{l, r} < k \le r}\{ f_{l, k - 1} + a_k \})。

因为 f 有单调性所以这个交点也有单调性，对于这两个滑动窗口单调队列即可。

U636032，数学8，by i_love_xqh。

这道题题意是让你求

棍母

这个应该是做不了的。不知道他为什么要出这种题。

11.27

代码源信心赛（存疑）。

T4 字典序最小，考虑贪心。

摸一下发现不是很能贪得出来，考虑 DP。

DP 直接做是单 log 的。5e6。不是很敢写。最后当暴力写了。没看到 3s。

然后每次数据范围 5e6 以上的时候，我觉得单 log 能过就过不了，我觉得不能过就能过。

快速找大模数下比较小的种子的逆元，保证模数和种子互质。快速是好写的意思。

找到 k 使得 k \cdot mod + 1 \equiv 0 \pmod{base}。不难发现 k 不会很大。

随机种子自然溢出要算逆元的时候比较好。种子要随机大于 1 的奇数。还要大于字符集大小，不然随便卡。状如 1 \times 10 + 11 = 2 \times 10 + 1。理论上来说还要小于模数减字符集大小。但是这道题字符集 1e9。不管了，反正随机种子自然溢出卡不掉。

https://heltion.github.io/anti-hash/

感觉打 CF 很好用。

T3 看着很典，想了一下发现是差分约束板子。

生成树上的状压不是很会。

这个树上点对间距离和等于每条边边权乘两侧点数乘积。

把无根树换成有根树，一条边的贡献就是子树大小乘总点数减子树大小。

然后就可以状压一个子树的答案。费用提前计算。

dyh 说和最小斯坦纳树差不多。

P3959。

我错了，我不该卡 jzy 的评测的。

这个按层 DP。

[COCI 2022.3] Fliper

\color{purple}★

每个板子建出上下两个点，能反射到的点连边，每个点度数不超过 2，就是有若干个环，有解的情况下要求每个环上四种颜色的点数量相同，且有若干点对要求颜色相同。

给每个环建一个点，有要求的点对就在对应环点间连边，就把点染色转化为了边染色。

然后跑一条欧拉回路，有解一定跑出来的是偶环，交替黑白染色，相当于用欧拉回路保证入度和出度相等。染完一次对每个颜色的子图再染一次。染 k 次染出 2^k 种颜色。

欧拉路径怎么找。

这个为什么是对的。

考虑 dfs 树。

[WF2022] Zoo Management 动物园管理

http://oi.nks.edu.cn:19360/zh/Problem/Details?cid=3172&tid=H

11.28

14:20 一中。

试了 Just_int_mian 说的两天前晚上熬夜。只在 NOIP 有用。感觉没什么用。

NOIP\tiny\text{——}\mathbb{N}\text{b\_jzy's h}\mathbb{O}\text{llow kn}\mathbb{I}\text{ght s}\mathbb{P}\text{eedrun }2025

CSP 考得好的同学也不要灰心。考得不好也不要骄傲。

感觉四道题是数学、DP、数据结构、图论，没有严格意义上的计数题，涉及至少一个冷门知识点。

8:00 科技楼楼下。准考证身份证文具食物饮料。

小丑。

哈基 Miku。纽带乐队。助我破鼎。老板说什么什么。喵喵喵。咕咕咕。日新月异。哈基米什么什么。二分图三元环计数。南北开关。小丑。🤡。🤡。🤡。后面的忘了，看一下。为什么不让中文名写长一点。请输入文本。并非又如何。不想写了。小丑。

11.30 C\mathbb{CCP} in \mathbb{C}hongqing

8:00 重大东门。

20:20 晚自习。

小丑。

Week 68

来不及
最后一句想你来不及让你知道
再也回不去
那个有彩虹出现的下午
再也感受不到你温度
如果你留我在梦里
我会放弃呼吸
请 超度我
若以色见我 以音声求我
是人行邪道 不 不能见如来
一切有为法 如梦幻泡影
如露亦如电 应作如是观
非空非有 亦空亦有
不生法相 无所住
非空非有 亦空亦有
不生法相 无所住

对不起
不经意就在你的影子里活下去
我不在意
不过是白日梦里一瞬息
为何还起念动心
怪你名字太熟悉
当我是一花一叶一春木
可否回到世界之初
请 超度我
若以色见我 以音声求我
是人行邪道 不 不能见如来
一切有为法 如梦幻泡影
如露亦如电 应作如是观
非空非有 亦空亦有
不生法相 无所住
非空非有 亦空亦有
不生法相 无所住
我的执念 万千千千
放不下地 放不下天
我把红线 折折剪剪
落入凡间 镜重圆

12.1

南开待遇这么好吗 考完NOIP还能放一周假 ——luoyudong

这个 yangjunjun 怎么比 lizuyan 还要小丑一个 luoyudong。

感觉 OI 选手（其实是特指我）很难注意到数值上的巧合。但是数学只会考这个东西。

www.bilibili.com/video/BV147411K7xu

讲的很好。突然又感觉能听懂数学课了。

零点不是点。

判断对数函数和常数的大小关系比对数函数求值简单。然后就可以用零点存在定理。

把一个函数拆成两个函数，就可以更好分别画图象。零点转交点。交点转零点。

偶函数有且仅有一个零点，则零点一定是 0。

求 f(f(x)) = a，换元，先求 f(u) = a 的解，再求 f(x) = u 的解。

定义域、解析式、值域。

单调性、奇偶性、周期性。

$(x_2 - x_1) (f(x_2) - f(x_1)) > 0$ 可以得到单调性。 抽象函数赋值。 已知单调性或奇偶性，可以把函数的大小关系转到变量上。 ## 12.3 以下的部分内容摘录自《刘擎西方现代思想讲义》。感谢语文老师。 --- 形而上学有三大信念： - 相信在感知的表象世界背后有一个更真实的本质世界。 - 相信这个混乱的世界实际上是有其目的的。 - 相信这个纷乱多样的世界背后有一种统一性。 尼采认为，那个所谓更真实的、有目的的、有统一性的本质世界根本不存在。我们之所以会编造这些东西，是因为人的心灵很脆弱。在这个纷乱繁杂的世界中，我们需要安慰。 如果我们相信虚假思想，就是把生命的希望寄托在不可靠的事物上面。当它们和生命本能冲突，我们就会怀疑这些虚假思想。结果是把我们寄托在上面的希望给打破了，人陷入虚无当中。 然而，虚无这个真相并不直接导致消极。认识到世界本无意义，这恰恰带来了创造的自由。 面对无意义的世界和无意义的生命，人应该立足于现实，直面无意义的荒谬，以强大的生命本能舞蹈，在生命活动中创造出价值。用尼采的话说，就是“成为你自己”。 这样一来，虚无不在会让你沮丧和绝望，反倒会给你最广阔的创造自我意义的空间，虚无让人变成了积极的创造者，这就是积极的虚无主义。 *登上顶峰的斗争本身足以充实人的心灵。应当设想，西西弗斯是幸福的。* ## 12.4 当我们说“这个杯子是一个杯子”和说“这个服务员是一个服务员”时，两种说法是有所不同的。因为物品的本质是与生俱来的，也无法自行将其改变；而人的本质是由自我意识决定的。 胡塞尔说，“意识总是对某物的意识”，也就是说意识有对象性。那么纯粹意识本身就是虚无。 如果人的存在就是意识，而意识本身是虚无，那么人的存在就是虚无，这就得出了“存在就是虚无”这个命题。 人为了获得一个本质，最直接的做法就是去模仿物，通过占有某种东西给自己一个定义。但这只是局部地、暂时地满足了对确定性的渴求，根本上的虚无是无法改变的，也就永远存在一种“徒劳的激情”推动我们去占有、去追求。 但因为存在先于本质，那么就没有什么预先给定的东西把我们固定住、束缚住。所以萨特说，人是被判定为自由的，自由就是人的命运，人唯一的不自由就是不能摆脱自由。 然而，自由选择会成为负担，因为选择必定会带来后果。你所有的选择，依据都是你自己，你做了选择的同时就确立了选择的判断标准。 人的存在有着无限展开的可能性，不被任何本质所限定。但这种轻盈的自由又是孤独而沉重的，因为你必须独自承担你所有的选择，独自承担自己的生命，你是自己“生命的孤证”。 ## 12.5 弗洛伊德的精神分析学说中把人格分为本我、自我和超我。 本我是人的本能欲望，是“无意识”的领域；自我是人的主观意识，用理性考虑无意识对欲望的要求；超我是人所接触的道德权威形成的理想人格，会通过内疚感和罪恶感影响人的心理和行动。 根据精神分析学说，理性的力量并没有那么强大，力量最强的其实是人的原始欲望，理性不过是在想办法应对这些原始欲望。这颠覆了启蒙传统中认为理性是人精神本质的观念。 当下，弗洛伊德的精神分析理论基本被主流心理学学术界否定，就像某些中文互联网的迷因中所展示的，其中的“反向形成”等概念使得其具备了不可证伪性，而不无论面对什么事实都能自圆其说的理论一定是伪科学。 但在另一方面，这种学说作为一种哲学或者文化理论，至今仍然具有深远而广泛的影响力。 ## 12.6 NOIp 总结 早上五点突然醒了，喝完一瓶东鹏特饮又睡着了。作息还是应该正常一点。 T1 好像没做特别久，但是最后有一个地方没判到挂了 5 分。 T2 想了很久，没有考虑出来这个解的形态。 T3 应该是最难的，但是赛上没意识到。没有想出来什么有道理的东西。 T4 感觉是比较典的数据结构，也没有想出来什么有道理的东西。 最后半个多小时彻底放弃了，写了每个题的最低档暴力。T3 是假做法。 95 + 20 + 24 + 20 = 159 这场主要的启发在于，虽然一场比赛中有 4 道或者 3*2 道题目，但是完全有可能有的题基本都会，有的题基本不会，而剩下的极少数题目想没想出正解会带来较大的区分度。 比如这场如果能做出 T2，然后就可以专心想后两题比较优秀的暴力，理论上可以得到将近 300 甚至以上的。 而如果一道题带来的区分度比较大，那是否擅长这个类型的题目也会有很大影响。比如我就不擅长计数题。 另一个方面来说，也没有太多做困难题目的经验。这场的题目推导起来还是比较麻烦的。模拟赛中也基本没有做出过难题，也基本不会在赛上专门去想。 在模拟赛中去磕难题一般是性价比较低的，分数大概率也会比别人低，但是这场都是难题，就导致没能想得出来。 这也说明做题不应止于模拟赛，应该自己找点有启发的东西做。 那如果我们的策略是没想出 T2 先打后两题的暴力的话，其实如果后面的题写了很久而 T2 其实多想一下就能想出来也会比较爆。 启发是我们应该有一个比较形式化的思考方式，使得对于可做题都能够在可接受的时间内被判定出来。然后就可以在考试的前一部分时间规划出每个题应该用多少时间打多少分。 还是把 NOIP 想简单了，主要策略是顺序开题开不动就打暴力，没有进行规划。 --- > 西风烈，长空雁叫霜晨月。霜晨月，马蹄声碎，喇叭声咽。 > > 雄关漫道真如铁，而今迈步从头越。从头越，苍山如海，残阳如血。 重新备战 NOIP。 ## 12.7 看了一下 cn4k。 目前得分最高的这篇，怎么说呢，就是起手是一个 5k 风格的末日公路文，中间是 cn2k 的 O5 吵架，最后单挑 aic，然后主题是一个有点老的神谕机决定论否定自由意志，中间几个反转和伏笔基本能猜到，但这也说明整体观感比较流畅，能一遍看懂。 虽然说几个点子都不算新，但还是有一些比较有道理的东西的。比如决定论在 cn3969 时就偏向于暴力对时间线剪枝得到稳定解，这篇就是至始至终只有一条确定的时间线。 > 如果意义必须建立在“能够改变最终结局”这一基础上，那么不仅是这个注定早逝的孩子，我们所有人的人生，连同人类文明的一切，所有的科学、艺术、爱与牺牲都将毫无意义。因为我们都会死，宇宙最终会走向热寂，一切都将归于虚无，这一切都会成为一场无人知晓的无意义闹剧。 --- 然后这个怪核（还是梦核？阈限空间？不是很了解）这一篇，主题是基金会对记忆删除剂的滥用。由于个人年龄原因一般不是很能有对这种风格的感觉，但还是比较新颖的。 --- 传汐引潮，这篇，感觉有点太空歌剧了，主要是打戏有点意义不明。吞噬制度性记忆的逆模因还可以，但是文章的重点又没有放在刻画这个上面。 # Week 69 ```text 你说这风景如画 我看你心猿意马 就别再听我说话 把伪装都卸下吧 你听见我在哭吗 反正也听不到吧 你像一匹白马 悠然自得逃跑吧 让我仔细看看你的模样 倒数着最后的谢幕时光 原谅我太早就收了声响 翩翩的你知道吗我满目痍疮 你听见我在哭吗 反正也听不到吧 你像一匹白马 悠然自得逃跑吧 让我仔细看看你的模样 倒数着最后的谢幕时光 我的白马儿呀你慢些跑啊 这一次没有我带你回家 春天啊暖阳啊快些来吧 保全他一路上无风无浪 我的白马儿你慢些跑啊 这一次没有我带你 回家 ``` --- 补课两周，文化课治好了我的退队倾向。 --- --- --- 字数统计：67605 字符