浅谈高斯(取整)函数(初步)
ShineEternal
·
·
个人记录
0.前言
高斯函数有多种类型,本文介绍 y=[x] 。
以 [x] 为主,文章可能还会涉及其他相关的函数。 (在 OI 中也会写为 \lfloor{x}\rfloor)
由于本文为初级篇,内容会循序渐进且较为基础。
1、引入
何为 y=[x]?
我们可以最直接的设想:
在数学表达中,有时需要表示出实数 x 的整数部分,例如人数,动物的只数等等。
每一种有需求的表达总需要一个对应的符号(不可能每时每刻用语言繁琐的描述)。于是,我们定义 [x] 为不超过 x 的最大整数。
举几个简单的例子:
$[-123.5]=-124$。
注意如果是负数 $-123.5$,我们卡一卡它的定义就可以发现答案不是 $-123$ 而是 $-124$。(~~初小高频考点~~)
特别地,当 $x\in Z$ 时,$[x]=x$。
## 2、定义与图象
### 2.1、定义
函数 $y=[x]$ 为取整函数。顾名思义,是取 $x$ 的整数部分。
但整数部分不是一眼望去的整数那一块(在负数上有体现),而是指**不超过 $x$ 的最大整数。**
查阅百度会发现, $[x]$ 也可以记作 $INT(x)$,因为在 C 语言中 int 取的就是一个数的整数部分。然而 $[x]$ 更为常用。
### 2.2、图象
我们回到 $y=[x]$。
通过观察不难发现,对于 $x\in [n,n+1)(n\in Z)$, $y=n$。
我们可以想象每个 $1$ 单位长度的小区间都对应到了同一个值上,也就是一条条坐标系中的线段。所以画出图来是这样:
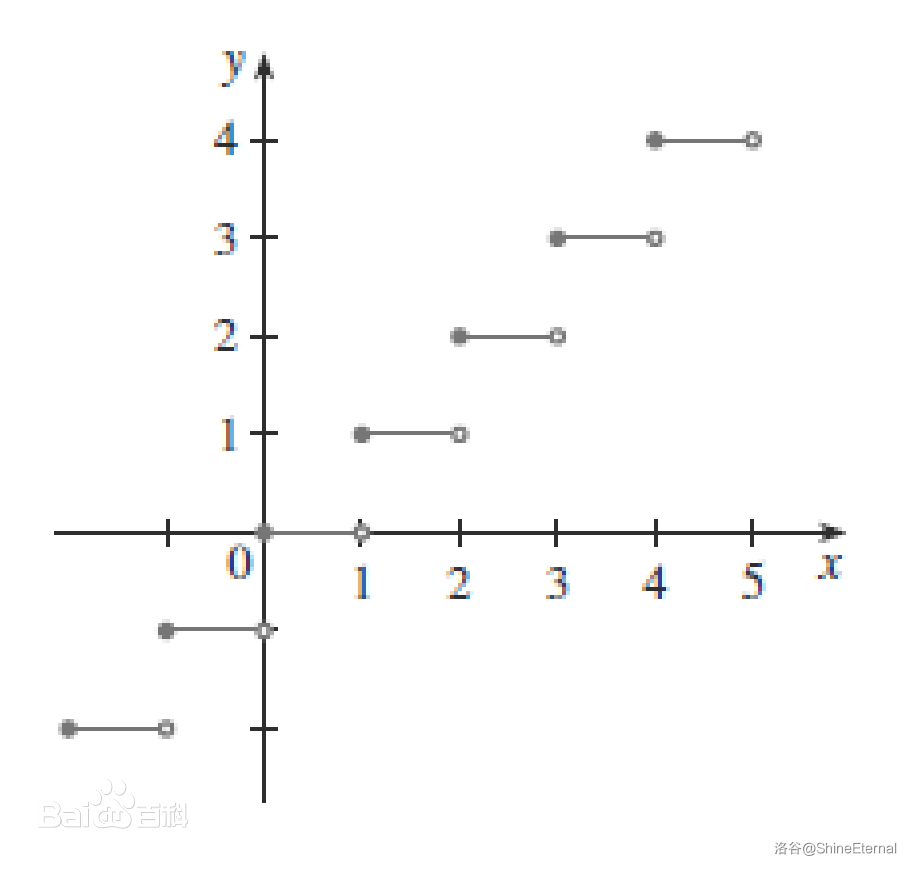
(图片来自百度百科)
经过总结,可以得出图象中如下几条简单的性质:
- 不减函数。
- 非连续性函数。
要注意的是,这个函数虽然大体看上去关于原点对称,但并不是[奇函数](https://baike.baidu.com/item/%E5%A5%87%E5%87%BD%E6%95%B0/107092?fr=aladdin)。
## 3、一些性质及配套例题
这一部分**一般**采用一条性质与一道例题配合呈现的形式。
---
#### 3.1 根据定义直接解题
求 $[\sqrt[3]{1+\sqrt[3]{2+\sqrt[3]{3+\dots+\sqrt[3]{2020}}}}]$ 的值。
这道题目的关键是在最终的取整上,这就省去的很大程度上的精度问题。
我们不妨考虑倒着算,由于精度要求不大,我们只需大体找出每一段的范围即可:
$\sqrt[3]{2020}<\sqrt[3]{2197}=13$;
$\sqrt[3]{2019+\sqrt[3]{2020}}<\sqrt[3]{2019+13}<13$;
$\sqrt[3]{2018+\sqrt[3]{2019+\sqrt[3]{2020}}}<\sqrt[3]{2018+13}<13$。
注意到上面运用了放大法,于是我们就一直把 $13$ 这个范围一直控制到:
$\sqrt[3]{2+\dots +\sqrt[3]{2020}}<\sqrt[3]{2+13}<7
这个 7 只是为了凑数方便,可以根据下面的步骤理解;
于是 \sqrt[3]{1+\sqrt[3]{2+\sqrt[3]{3+\dots+\sqrt[3]{2020}}}}<\sqrt[3]{1+7}=2
这样,我们可以总结出 1<\sqrt[3]{1+\sqrt[3]{2+\sqrt[3]{3+\dots+\sqrt[3]{2020}}}}<2
(左边的 1< 是因为 \sqrt[3]{1}=1,再加些东西一定比一大。 )
所以,[\sqrt[3]{1+\sqrt[3]{2+\sqrt[3]{3+\dots+\sqrt[3]{2020}}}}]=1。
3.2:定理 1
3.2.1:描述
#### 3.2.2:证明:
$x-y\geq 1$ 即 $[x]+\{x\}-([y]+\{y\})\geq 1$。
---
**补充关于 $\{x\}$ 的定义:**
$\{x\}=x-[x]$。
用语言来描述,就是 $x$ 的小数部分。
---
移项得 $[x]-[y]\geq 1+\{y\}-\{x\}> 0
这时因为 [x]-[y]\in Z,所以可由 [x]-[y]>0 得到 [x]-[y]\geq 1。
3.2.3:相关例题
求 [\frac{1^2}{2015}],[\frac{2^2}{2015}],[\frac{3^2}{2015}],[\frac{2015^2}{2015}] 中共有多少不同的整数。
观察发现,到了一定的值 [\frac{n^2}{2015}](n\in [1,2015])后,每一项均会与前一项的值不同。
而在 [x] 意义下的不同的值至少要相差 1。故可转换为数学语言,也就是
[\frac{n^2}{2015}]-[\frac{(n-1)^2}{2015}]\geq 1
由上面的性质,我们知道可以把取整符号去掉,只需要
\frac{n^2}{2015}-\frac{(n-1)^2}{2015}\geq 1
就行啦!
最终解得 n\geq 1008。
此时我们把 2015 项分成了两批:
所以最终的答案为 503+1009=1512 个不同的整数。
3.3:定理 2
3.3.1:描述
对 \forall x\in R,有 [x]+[x+\frac{1}{2}]=[2x]。
3.3.2:证明
当 0\le \{x\}<0.5 时,
3.3.3:相关例题
对 \forall n\in