后缀自动机(SAM) 学习笔记
chlchl
·
·
算法·理论
前言
SAM 这东西,很难,非常难,特别难。第一遍看不懂,没关系,可以换下一篇,看不懂再换,换多几篇,迷迷糊糊就懂了。
不过,这俩篇东西真的挺有价值的:
- 史上最通俗的后缀自动机详解(这一篇很有名)。说实话,我真不觉得这篇东西讲得有多好,只是相对比较清楚罢了。
- [学习笔记] 后缀自动机。这篇倒不错,比较易懂,就是没有图。
- 题解 P3804 【【模板】后缀自动机 (SAM)】,这篇图很详细,很易懂,但是略显简略,对于求知欲强的同学们比较难受(因为几乎没有证明,全是结论)。
看完这三篇,你大概率是不懂或似懂非懂的(为啥呢?因为一个没有图,一个图难懂,并且都没有明显举例,还有一个太简略)。
虽然我努力想要写出更好理解的博客,但奈何自身实力太菜,实在干不出精华,大家将就着看吧,轻喷哈。
当然,我知道这是个痛苦的过程。所以我会用语言营造一个比较轻松的氛围,让读者有一种亲切感。正因如此,虽然本博客规范使用 \LaTeX,但肯定是过不了题解审核的(太严了,啥都要证明)。
概念
SAM 就是一棵以后缀形式维护一个字符串所有子串的树。它可以在 O(n) 的时空复杂度完成很多看似只能 O(n^2) 完成的逆天操作。
说白了,后缀自动机就是一个中心思想,两棵树,四个基本引理构造出来的 bt 玩意儿 ,但它又是目前这个难度处理字符串最牛逼的数据结构。
学吧,很难学,很难弄;不学吧,考场又没分,你说怎么办?
万恶之源中心思想——endpos
### 引理
关于这个 $endpos$,有四点引理需要知道(这可能会跟那两篇东西很像,因为我就是跟着那两篇自学的)。
> **引理 $1$:如果两个非空字符串 $s$、$t$(假设 $|t|\leq |s|$)满足 $endpos(s)=endpos(t)$,则 $t$ 必定为 $s$ 的后缀。**
不证明了,这么明显的结论直接感性理解。证了反而弄不懂了。比如 $abcabcabc$ 中,$endpos(bc)=endpos(abc)=\{3,6,9\}$,$bc$ 也是 $abc$ 的后缀。
> **引理 $2$:对于两个非空字符串 $s$、$t$(假设 $|t|\leq |s|$),它们的 $endpos$ 必定满足如下关系:**$\begin{cases}
endpos(s)\in endpos(t)\qquad {\color{black}\colorbox{white}{(t 是 s 的后缀)}} \\ endpos(s)\cap endpos(t)=\emptyset\quad {\color{black}\colorbox{white}{(t 不是 s 的后缀)}}\\
\end{cases}$。
注意,是**长度小的集合包含大的集合**。
这也很好理解吧?不证了,毕竟只是一篇教程(或者说留给自己复习的),用不着(也做不到)全证一次。
例:$aababaab$ 中,$ab$ 是 $aab$ 的后缀, $endpos(aab)=\{3,8\},endpos(ab)=\{3,5,8\}$。显然 $endpos(ab)\subseteq endpos(aab)$。
> **引理 $3$:对于每一个 $endpos$ 等价类,其对应的子串长度是单调递减的。**
这个也比较明显,也举个例:例如,在 $aaabaaabaaab$ 中,$endpos()=\{4,8,12\}$ 的分别是 $aaab,aab,ab,b$,也是十分直观。
浅说下理由吧:如果一个等价类中,最长的($aaab$)和最短的($b$)都在,那长度在中间的($aab,ab$)肯定也在。
~~看不懂?算了,别纠结,知道就好,下一个。~~
> **引理 $4$:$endpos$ 等价类的数量为 $O(n)$ 级别的。**
这个需要亿点点证明(改自第一篇的同一引理的证明):
根据引理 $1$,我们在一个字符串前加上一个字母,其 $endpos$ 集合一定是原串的一个子集;并且根据引理 $2$,添加两个不同字符,$endpos$ 必定没有交集(不存在后缀关系)。那么我们可以认为,添加字符的过程就是对原串 $endpos$ 集合的一次划分。而这些划分出来的子集数量不会超过原集合大小,又考虑到所有集合都是 $\{1,2,\cdots,n\}$ 中分出来的,所以数量的确是 $O(n)$ 的。
什么?你还是看不懂?额,举个简单的例子帮助理解。
假设有字符串 $aababaab$(没错又是它)。
1. 现在我们要把整个字符串划分成两类,那肯定是 $a$ 一类,$b$ 一类。所以我们得到下面两个集合:$endpos(a)=\{1,2,4,6,7\},endpos(b)=\{3,5,8\}$。
2. 考虑 $a$ 这边的分支。明显,在 $a$ 的前面可以添加 $a,b$,所以又得到 $endpos(aa)=\{2,7\},endpos(ba)=\{4,6\}$。你会发现没了 $1$,但问题不大,后面解释。
3. 换一边,考虑 $b$。显然 $b$ 前面可以塞 $a$,却不能塞 $b$(因为没有 $bb$ 这个子串)。所以我们得到 $endpos(ab)=\{3,5,8\}$。
差不多了,能理解怎么分的就行,至于什么线性不线性的,记住时空复杂度都是 $O(n)$ 即可。
### Parent Tree
> 成功的自动机,都有一棵树在默默付出。$\qquad$——在某篇博客看到的。
AC 自动机有 Trie,回文自动机也有 Trie(算半个)。那 SAM 有啥?
答案是 Parent Tree。我们现在有 $n$ 个 $endpos$ 集合。显然,需要数据结构,即一棵树来维护它。考虑到引理 $2$ 中,不同集合之间会出现包含关系,所以我们以含有包含关系的两个集合为父子,并连边,就形成了 Parent Tree。由于两个类要么包含,要么无交集,所以不会出现主席树一样的~~一妻多夫~~一个节点多个爸爸。
如图,我们对 $aababaab$ 做 Parent Tree:
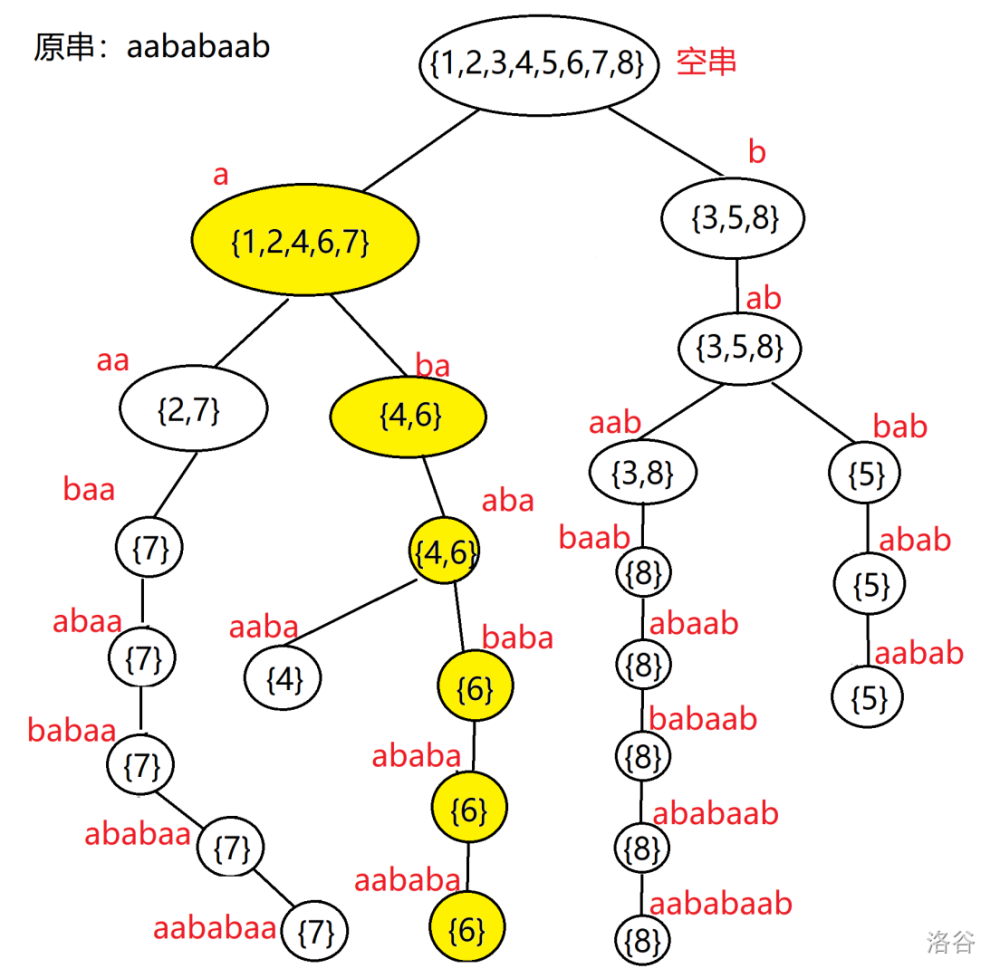
容易发现,Parent Tree 上,父节点对应串长度 $+1$ 就是子节点对应子串长度了。
Parent Tree 十分重要,甚至比 Trie 在 AC 自动机的地位还要重要(因为难),所以务必完全理解 Parent Tree 再看 SAM(~~没错,这么大篇幅全是铺垫~~)。
## SAM 的构建
说了这么多,SAM 到底长啥样呢?
其实,刚刚的 Parent Tree 已经给出了答案:SAM 所用到的节点就是 Parent Tree 上的节点,只是连边不一样罢了。
说一下 SAM 的一些定义:
- 源点:Parent Tree 上的根节点。
- 终止节点:最长子串(即原串)所在点及其 Parent Tree 上的祖先(标黄标错了,应该是 $\{8\}$ 那一列)。
- 后缀自动机的边数为 $O(n)$ 级别的。这个我实在证不出来,有兴趣的去看看第一篇博客吧。怎么记?不用记,你只需要知道 SAM 时空都是 $O(n)$ 即可。
- SAM 与 Parent Tree 的主要区别是:SAM 的边是在子串后添加字符得到,而 Parent Tree 是在前面。正因如此,它们结合在一起后,拥有无比强大的功能和优美的性质。
~~WTF?你说 SAM 前凸后翘??想什么???~~
那来张图看看 SAM 长啥样吧(对字符串 $aababaab$ 建 SAM)。
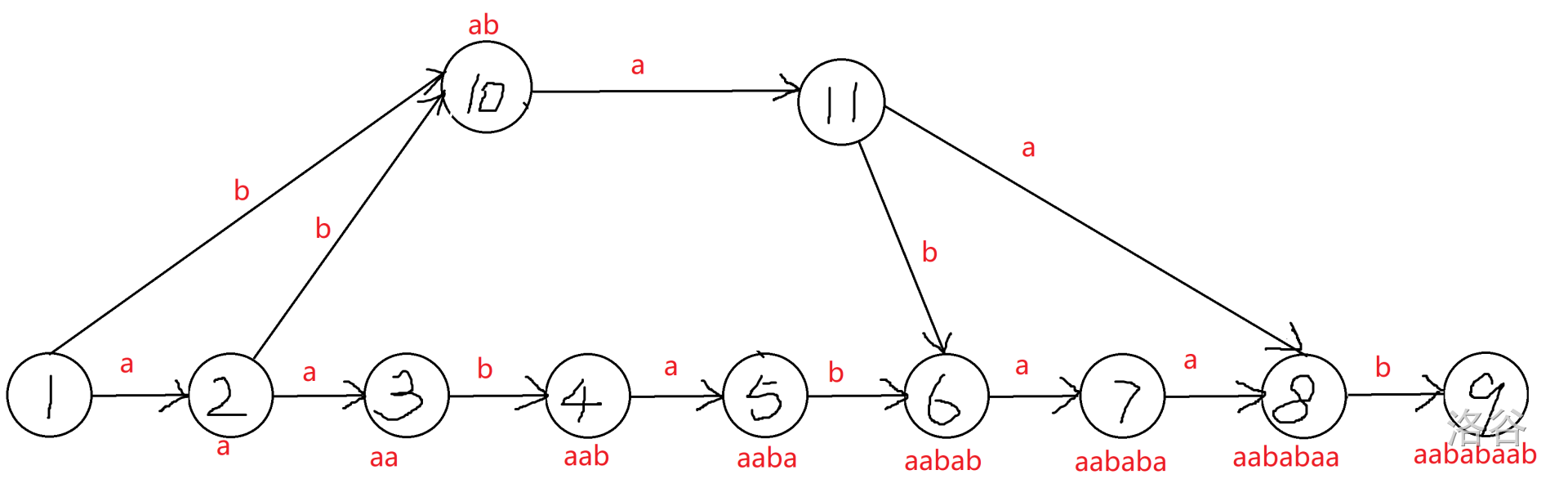
你肯定疑惑:这什么高科技连边?没关系,你只要知道,这些边保证了所有子串的出现就行。
以下是 SAM 的基本结构:
1. 下面整齐的一行,从左往右走分别是该字符串的前缀(长度递增,包括原串)。
2. 而这样肯定缺了很多子串。所以,我们需要连一些上面的边,甚至新增节点($10$ 号点和 $11$ 号点),保证所有子串**不重复地**出现出现在 $1$ 到某个节点的路径中。
3. 根节点到每个节点的所有路径,必定构成**所有前缀的所有后缀**。即 $1\rightarrow 2\sim 9$ 的任意一条路径,组成的字符串都是 $2\sim 9$(最下面那一行)的某个节点所代表的字符串的后缀。又因为这个字符串本身就是原串的前缀,所以就有了所有前缀的所有后缀这个说法。
至于这个不重复,你可以从以下两点理解。
1. SAM 是一个所有满足一个字符串的所有子串都出现的自动机中的最小的,证明它的节点数和边数都是最少的。
2. 如果有重复,意味着某个点的出边中有两条一模一样的字母边,这是绝对不允许的(详见 Trie,一样的)。
这里,我总结出 SAM 的构造步骤,简单易懂,适合新手:
1. 先画出最下面一行(这个应该都会画吧)。
2. 依次考虑每个前缀的后缀是否能走出来。
3. 如果都能,则下一个。如果不能,考虑连一条新边。这条边应满足加上之后,所有**经过这条边的路径**组成的字符串**都是原串的子串**(可能有多种连法,但只有一种是正确的)。换句话说,连完这条边,不能走出来一个在原串中没有出现的东西。
4. 所有节点都连完后,检查是否有节点出边冲突(即有多条同一字母的边)。
5. 如果某个点 $u$ 发生冲突,找到所有边连向的节点 $v$ 的 LCF($\text{Longest Common Suffix}$,即最长公共后缀),在上方新建一个节点代表这个 LCF(就是类似 $10,11$ 号点)。连 $u\rightarrow LCF$。
6. 检查改完之后所有节点有没有遗漏了某些子串,如果有遗漏返回步骤 $3$(不过注意,尽量在新节点连边,不然很可能连完新建节点,发现又在同一个位置冲突……)。
7. 如果这个节点新建完成且没有冲突,返回步骤 $5$,检查下一个。
有点长,还请耐心看完。毕竟这是我自己发明的,~~新手发明的应该对新手比较友好~~。
下面,我们一起看看构建过程。~~什么?要代码?急个啥,还没轮到它出面呢 qwqqq~~。
1. 画出下面一行的前缀,如图。
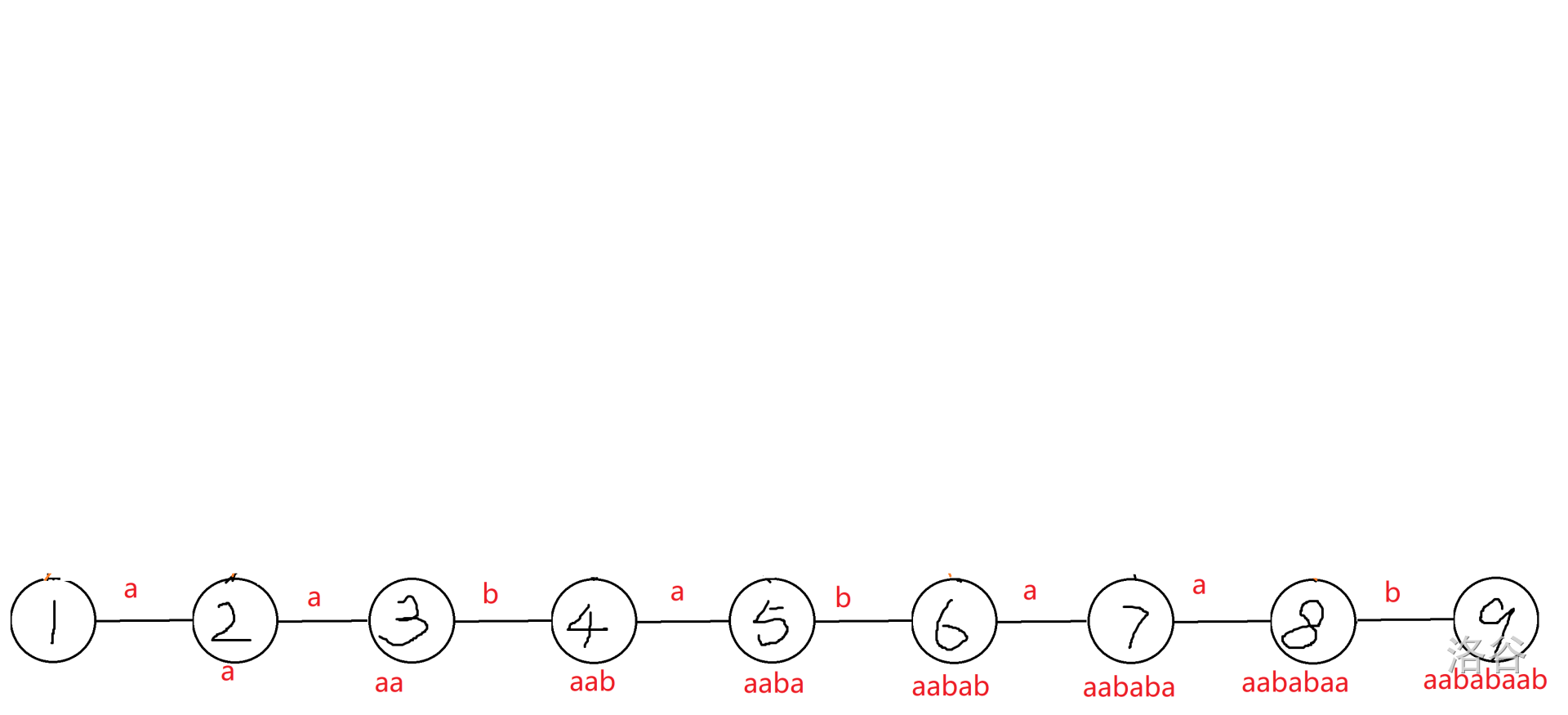
2. 前三个都没有遗漏,第四个 $ab,b$ 均没有出现,所以考虑从 $1,2$ 向 $4$ 连 $b$ 边。这样,$1\rightarrow 4=b,1\rightarrow 2\rightarrow 4=ab$(上面步骤没看懂的可以在这里结合理解)。至于为什么是从 $1,2$ 连边,自己推的时候上帝视角看即可,代码实现待会再说。
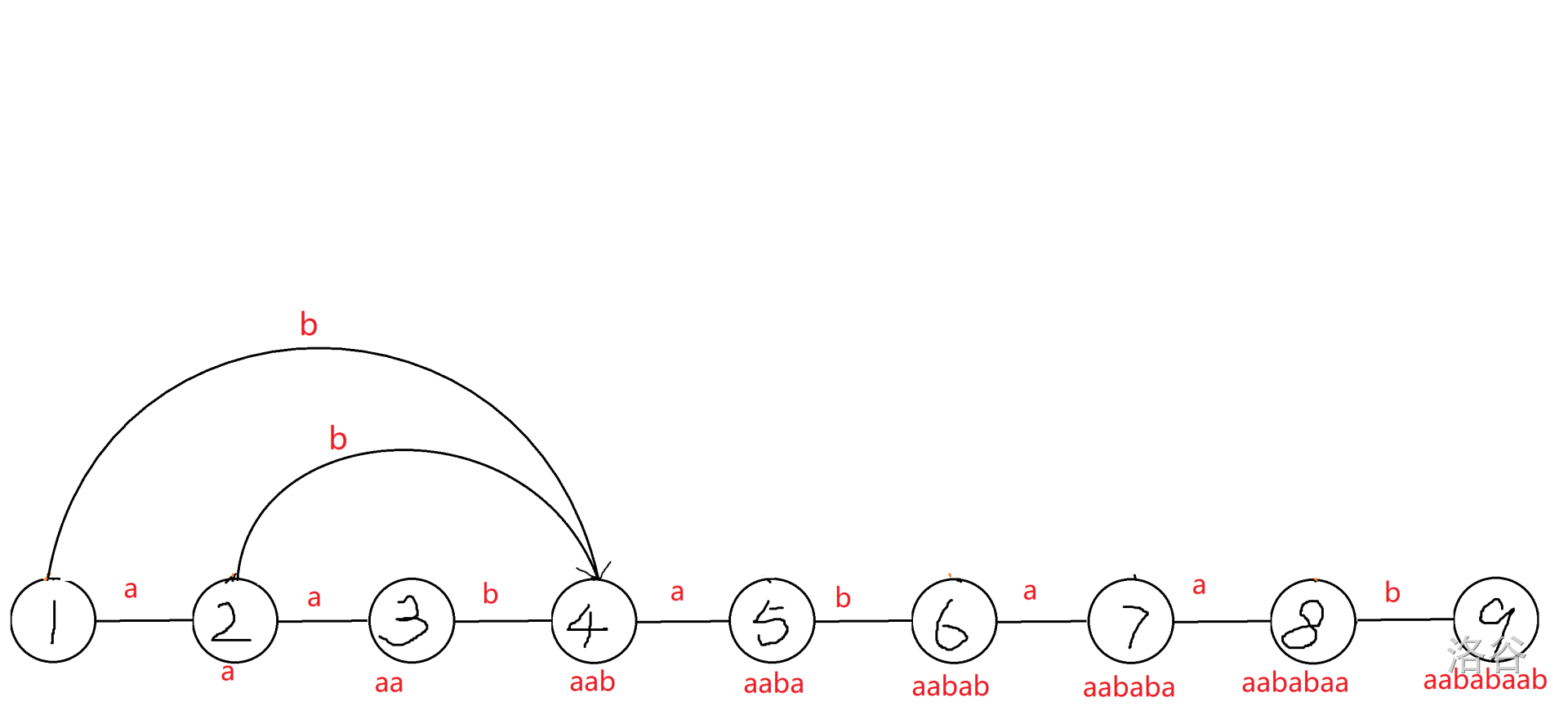
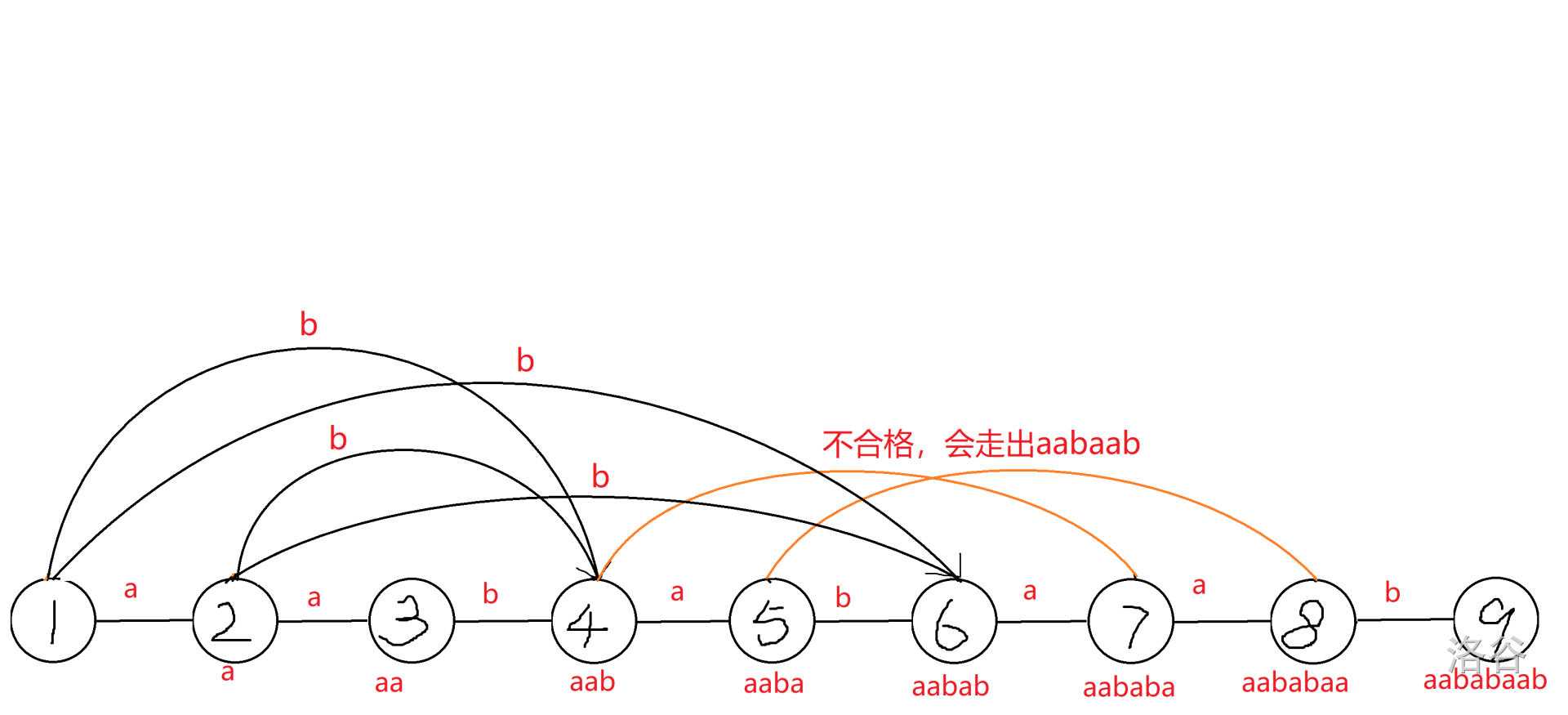
3. 再次检查,发现 $8$ 没有出现 $baa$ 等若干后缀。这时,三种连边方案(两种橙色的,一种黑色的)中,橙色的两种连上 $a$ 边之后,会走出 $aabaab$,而这个不是原串的子串,所以不行。黑色的就可以。
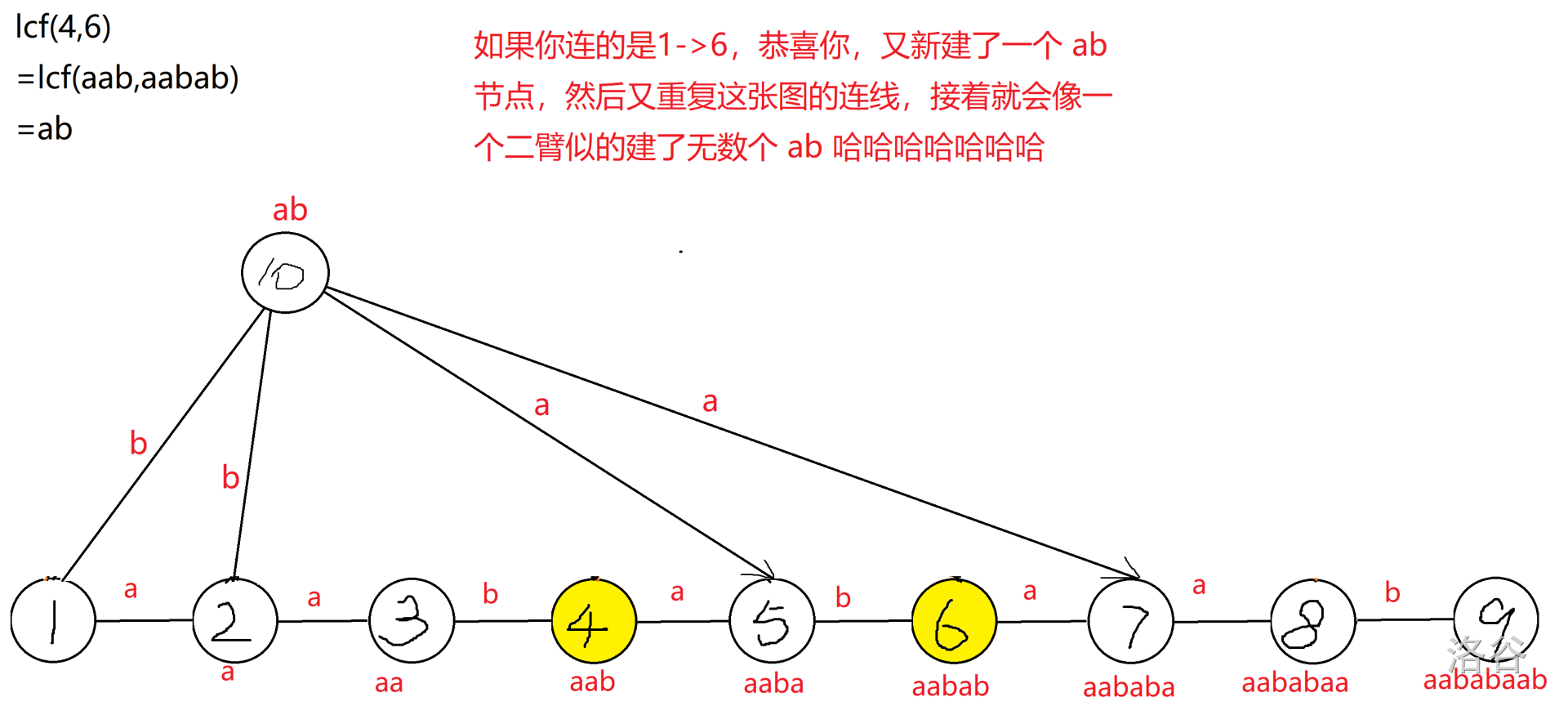
4. 没有遗漏了,但是 $1,2$ 都冲突了。由于 $1,2$ 两条边连向的点一样,所以我们放在一起讨论。这两条边连向的是 $4,6$,因为 $LCF(4,6)=ab$,所以新建 $ab$ 节点,从 $1,2$ 连 $b$ 边。同时,发现 $5,7$ 号分别没有 $aba,ba$ 等后缀,所以分别向 $5,7$ 连 $a$ 边。
5. 很遗憾,又冲突了。这次冲突的是 $5,7$ 号点,又因为 $LCF(5,7)=aba$,所以新建 $aba$ 节点,连 $10\rightarrow 11$。检查发现 $6,8$ 号点没有 $bab,baa$ 等后缀,所以分别向 $6,8$ 号连 $b,a$ 边。
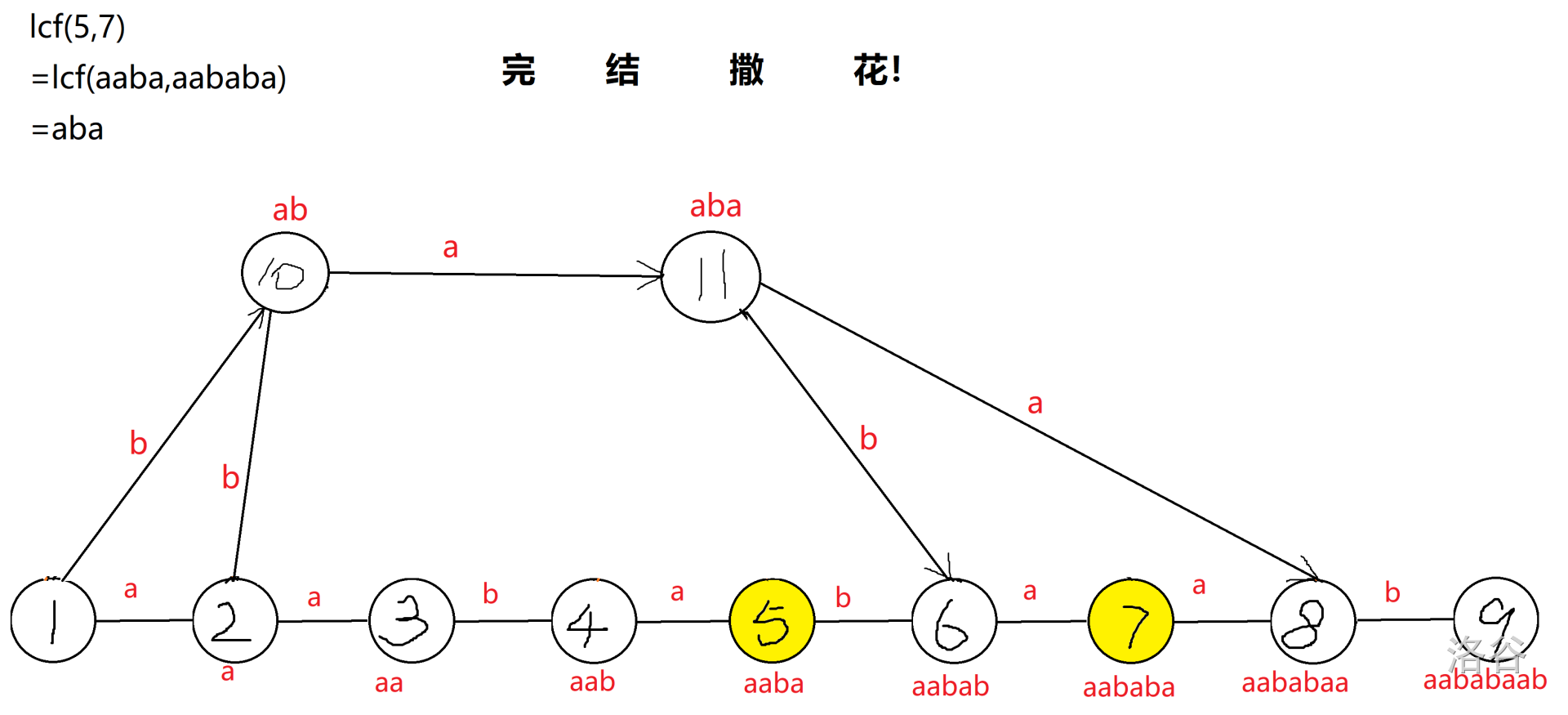
至此,所有节点均无遗漏、冲突,后缀自动机建立完成!
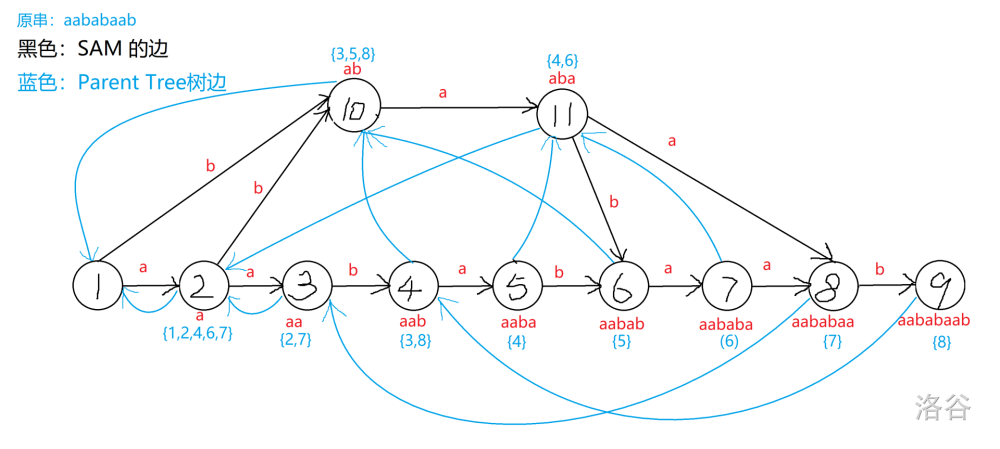
不过,建出来之后,我们可以将 Parent 树的树边连上。连完之后如图(高能警告):
## 代码构建
~~说了这么多,大家终于可以见到仿佛已经几十年没见面的代码了。~~
很遗憾,代码实现跟上面手动构建的方法完全不一样(或者说没什么关系)。但手动构建的方式一定要学会,因为这是利用样例探究做法的必备技能。
先放个代码?
```cpp
void insert(int c){
int u = lst, v = ++tot;
lst = tot, sam[v].len = sam[u].len + 1;
while(u && !sam[u].son[c]) sam[u].son[c] = v, u = sam[u].fa;
if(!u) sam[v].fa = 1;
else{
int p = sam[u].son[c];
if(sam[p].len == sam[u].len + 1) sam[v].fa = p;
else{
int q = ++tot;
sam[q] = sam[p], sam[q].len = sam[u].len + 1;
sam[p].fa = sam[v].fa = q;
for(;u&&sam[u].son[c]==p;u=sam[u].fa) sam[u].son[c] = q;
}
}
}
```
对于这个代码,我不想废话,~~一方面是因为真的很无语~~,另一方面是因为讲也讲不好。直接一波~~弱势图解~~连图讲解,文字都在图片里。
只能告诫各位,看讲解的时候,一定要分清楚,哪个是 Parent Tree,哪个是 SAM……蒙了我好久。
~~**图片高能预警**~~。
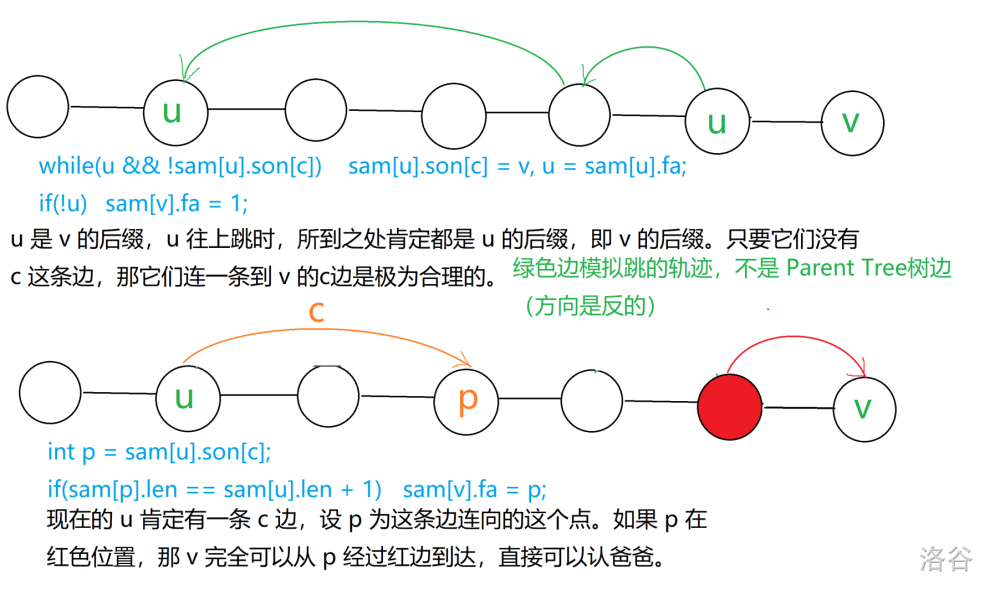
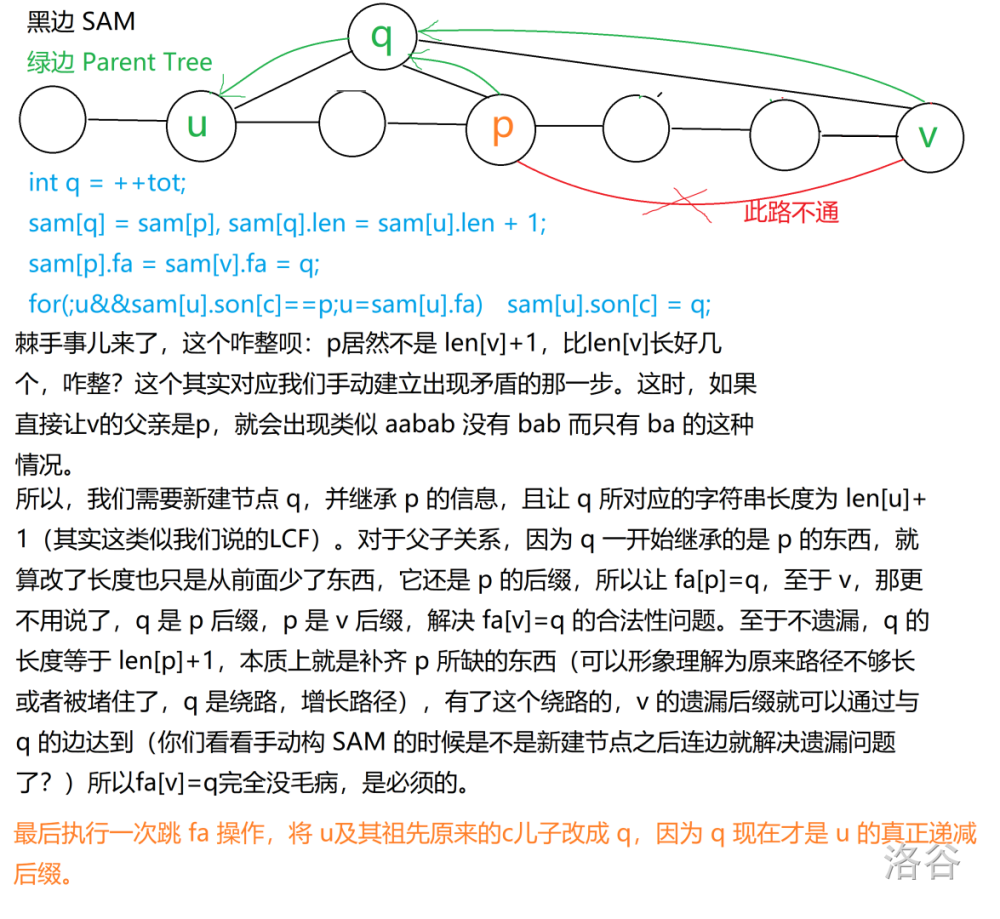
如果还是不清楚,建议可以再去开头第一篇,他这个部分讲得还是不错的。
到这,SAM 的原理讲完了。终于轻松了。
## 应用
SAM 可以被应用在子串判断、统计、求多串最长公共子串、字典序第 $k$ 大等问题,并且拥有者极为优秀的时空复杂度。
这里只用模板题作例子:[P3804 【模板】后缀自动机 (SAM)](https://www.luogu.com.cn/problem/P3804)。
这题求的是字符串中所有出现次数不为 $1$ 的子串的出现次数乘上该子串长度的最大值。
我们建出 SAM 后,统计一下每个单词的出现次数 $sz$。因为后缀自动机刚好不重不漏地记下了所有子串,所以我们直接父亲连儿子,树形 DP 给它切掉。
代码:
```cpp
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N = 1e6 + 10;
char s[N];
int n, lst = 1, tot = 1;//记得初始化这俩玩意儿
ll ans;
struct SAM{
int len, fa, sz, son[30];
SAM(){memset(son, 0, sizeof(son)), fa = len = sz = 0;}
} sam[N << 1];
vector<int> g[N << 1];
void insert(int c){
int u = lst, v = ++tot;
lst = tot, sam[v].len = sam[u].len + 1, sam[tot].sz = 1;
while(u && !sam[u].son[c]) sam[u].son[c] = v, u = sam[u].fa;
if(!u) sam[v].fa = 1;
else{
int p = sam[u].son[c];
if(sam[p].len == sam[u].len + 1) sam[v].fa = p;
else{
int q = ++tot;
sam[q] = sam[p], sam[q].sz = 0, sam[q].len = sam[u].len + 1;//一定要将q的sz设为0!复制的就是盗版的,盗版的还是盗版的,不能算出现过
sam[p].fa = sam[v].fa = q;
for(;u&&sam[u].son[c]==p;u=sam[u].fa) sam[u].son[c] = q;
}
}
}
void dfs(int u){
for(int v: g[u]){
dfs(v);
sam[u].sz += sam[v].sz;//统计sz,即出现次数
}
if(sam[u].sz != 1) ans = max(ans, (ll)sam[u].sz * sam[u].len);//更新答案
}
int main(){
scanf("%s", s);
n = strlen(s);
for(int i=0;i<n;i++) insert(s[i] - 'a');
for(int i=2;i<=tot;i++) g[sam[i].fa].push_back(i);//建边,准备树形 DP
dfs(1);
return printf("%lld\n", ans), 0;
}
```