亿些好玩的 MO 题目
Scrutiny
·
2020-08-01 16:14:52
·
个人记录
这里收录的题目不一定难,但一定很有意思(
尽量做到周更,每次五题左右。转载请注明出处,谢谢。由于此处图片用的是洛谷图床,若要在站外引用请自己用其它图床上传。
想要解答者请在洛谷私信笔者 LFC_伟大的哲学。请注明需要解答的题号 。想要投稿也可私信。
题目如有侵权,或答案有问题也请联系笔者。
题目难度共 10 种,分别为 1,2,3,4,5,6,7,8,9,10 。求评难度 /kel
难度 0 大约对标 初中 / 高中课内内容。
难度 1,2 大约对标 大同中学杯初赛
难度 3 大约对标 大同中学杯复赛
难度 4 大约对标 全国高中数学联赛预赛(弱省)
难度 5 大约对标 全国高中数学联赛一试
难度 6 大约对标 全国高中数学联赛一试+/二试-
难度 7 大约对标 全国高中数学联赛二试+/中国东南地区数学奥林匹克-
难度 8 大约对标 中国东南地区奥林匹克/CMO-
难度 9,10 大约对标 CMO/其他 MO 强国奥林匹克
第一期:
$2.$难度:$3
已知正整数 x>1 ,并且 10000\mid[\dfrac{x^8}{x-1}] ,这里 [a] 表示 a 的整数部分,求 x 的最小可能值.
3.$难度:$6
若 α,β,γ 为实数, y=\sum\mathrm{cos\space \alpha+\sum cos\space| \alpha-\beta|} ,求 y 的最小值.
4.$ 难度:$7
对于实数数列 \{a_i\},\{b_j\} ,求证:\sum\limits_{m,n=1}^{2022}\dfrac{a_m b_n}{(\sqrt{m}+\sqrt{n})^2} \leq 2(\sum\limits_{m=1}^{2022}a_m^2)^{\frac{1}{2}}(\sum\limits_{n=1}^{2022}b_n^2)^{\frac{1}{2}} .
5.$难度:$3
------------
### 第二期:
$6.$难度:$1
已知点 P(3,4) 在以原点为圆心的圆 O 上,在 y 轴上取两点 E,F ,使得 PE=PF ,且点 E 在点 F 上方。若直线 PE,PF 分别交圆 O 于点 C,D ,试求直线 CD 的斜率.
(注:此题标答是解析硬算,但几何方法只需一行即可做完)
7.$难度:$2
在锐角 \triangle ABC 中,AA_1,BB_1,CC_1 分别是高线、中线、角平分线,且 \triangle A_1B_1C_1 是正三角形。证明:\triangle ABC 是正三角形。
8.$难度:$2
求证:对任意正整数 m ,有 \sum\limits_{d|m}φ(d)=\sum\limits_{d|m}φ(\dfrac{m}{d})=m .其中 φ(x) 是欧拉函数.
9.$难度:$4
关于 x 的实系数方程 x^4+ax^3+bx^2+ax+c=0 恰有 3 个不等实根,分别为 \tan\alpha,\tan 2\alpha,\tan 3\alpha ,其中 \alpha\in(0,\pi) 。试求 \alpha 的所有可能值.(题目来源:2019 年西班牙数学奥林匹克)
10.$难度:$7
设正数 x,y,z ,求证:(xy+yz+zx)(\dfrac{1}{(x+y)^2}+\dfrac{1}{(y+z)^2}+\dfrac{1}{(z+x)^2})\ge\dfrac{9}{4} . (题目来源:1996 年伊朗 IMO 国家队选拔考试)
第三期:
11.$ 难度:$4
在 \triangle ABC 中,证明:\dfrac{a}{b+c-a}+\dfrac{b}{c+a-b}+\dfrac{c}{a+b-c}≥\dfrac{b+c-a}{a}+\dfrac{c+a-b}{b}+\dfrac{a+b-c}c≥3 .
12.$难度:$3
如图,在定矩形 ABCD 中,AB=9,AD=6,BE=3 ,E 在 BC 上。F 是圆 B 上的一动点,∠GAF=\dfrac{\pi}{2},\dfrac{AF}{AG}=3 ,求 CG 的最小值.
在锐角 $\triangle ABC $ 中,点 $H,O$ 分别为垂心、外心,$F$ 为 $CD$ 中点,试证明:线段 $EF$ 平分线段 $HO$.
(这张图有点乱,这边建议自己画图
$14.$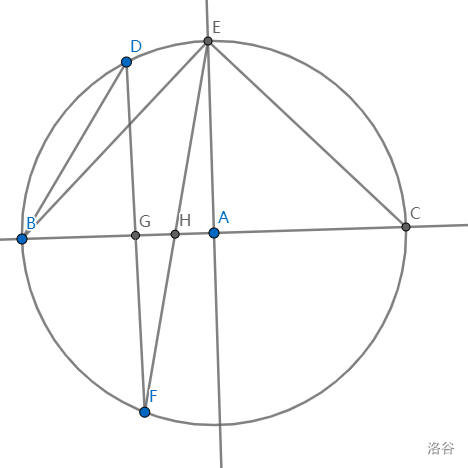
已知直径 $BC=1$,线段 $BD=\dfrac{3}{5}$,且 $BE=EC$。
点 $F$ 为直线 $BC$ 下方,圆 $A$ 上的一个动点。试求线段 $GH$ 的最大值.(题目来源:AIME)
$15.$难度:$3$ 求证:任意四边形的四条边长度的平方和等于对角线的平方和与对角线中点连线的平方的和的四倍.
------------
### 第四期:
$16.$难度:$5$ 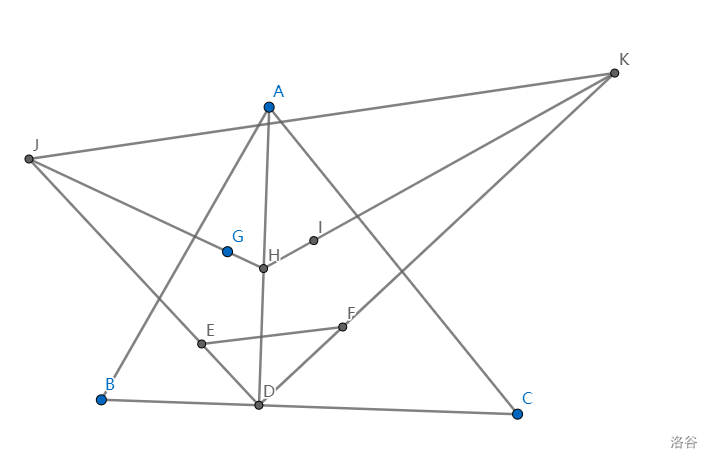
如图,$H$ 为 $\triangle ABC$ 的垂心,$E,F,G,I$ 分别为 $\triangle ABD,\triangle ACD,\triangle ABH,\triangle ACH$ 的垂心。求证:$EF\| JK$.
$17.$难度:$5
对于 \forall k\in[1,n]\bigcap \mathbb{z}^+ ,有 a_k\in[\dfrac{1}{2},1] 。求证:\prod\limits_{i=1}^na_i+\prod\limits_{i=1}^n(1-a_i)\ge\dfrac{1}{2^{n-1}} .
18.$难度:$3
求证:不存在 100 个互异的正整数,使得其中任意 98 个数之和能被另外两个数的和整除.
19.$难度:$4
求证:
如图,A,B,C 共线,D,E,F 共线。证明:G,H,I 共线.(帕普斯定理)
20.$难度:$2
设正实数 x,y>1 ,且 a=\sqrt{x-1}+\sqrt{y-1} ,b=\sqrt{x+1}+\sqrt{y+1} 。若 a,b 为两个不相邻的正整数,试求 x,y .
第五期:
21.$难度:$6
设 0<b\le a<1 ,求证:a^a+b^b\ge a^b+b^a .
22.$难度:$8
设整数 n\ge 3 ,\alpha,\beta,\gamma\in(0,1) ,且非负实数数列 \{a_n\},\{b_n\},\{c_n\} 满足 \sum\limits_{i=1}^{n}(k+\alpha)a_k\le\alpha,\sum\limits_{i=1}^{n}(k+\beta)b_k\le\beta,\sum\limits_{i=1}^{n}(k+\gamma)c_k\le\gamma 。\sum\limits_{k=1}^n(k+\lambda)a_kb_kc_k\le\lambda ,试求 \lambda_{\min} .(题目来源:2014 东南数学奥林匹克)
23.$ 难度:$5
设函数 f(x) 定义域为 \mathbb{R} ,且对于任意实数 x_1,x_2 ,都有 f(x_1)+f(x_2)=2f(\dfrac{x_1+x_2}{2})f(\dfrac{x_1-x_2}{2}) .f(\dfrac{\pi}{3})=\dfrac{1}{2},f(\dfrac{\pi}{2})=0 ,试求 f(x) 的最小正周期并加以证明.
24.$ 难度:$4
在圆内接四边形 ABCD 中,BC×CD=BA×DA 。若 AB,BC,CD,DA 的长度为四个小于 15 的正整数,求 BD_{\max} .
25.$ 难度:$5
设 x>0,n\in\mathbb{Z^+} ,证明:\sum\limits_{k=1}^n\dfrac{x^{k^2}}{k}\ge x^{\frac{n(n+1)}{2}} .
第六期:
26.$ 难度:$6
在 \triangle ABC 中,AD 平分 \angle BAC ,F 为 BC 中点。\triangle ADF 的外接圆与 \triangle ABC 的外接圆交于 E,G ,H 为 EG 中点。求证:AD \parallel HF .
27.$ 难度:$6
对于任意正整数 i\in[1,n] ,有 a_i,b_i,c_i,d_i,e_i\ge1 。 记 A=\frac{1}{n}\sum\limits_{i=1}^na_i,B=\frac{1}{n}\sum\limits_{i=1}^nb_i,C=\frac{1}{n}\sum\limits_{i=1}^nc_i,D=\frac{1}{n}\sum\limits_{i=1}^nd_i,E=\frac{1}{n}\sum\limits_{i=1}^ne_i \prod\limits_{i=1}^n \dfrac{a_ib_ic_id_ie_i+1}{a_ib_ic_id_ie_i-1}\ge(\dfrac{ABCDE+1}{ABCDE-1}) .
28.$ 难度:$5
证明:对于 \forall n\in \mathbb{Z^+} ,有 n-\ln(n+1)<2(1+\sum\limits_{i=1}^n\dfrac{i}{i+1}) .
29.$ 难度:$6
已知正整数 n 与素数 p,q,r 满足 \dbinom{n}{3}=pqr ,且 p,q,r 在一个公差为 336 的等差数列中。试求 n_{\min} .(题目来源:2020\ \text{Nordic} )
30.$ 难度:$5.5
若正整数 m,n 满足 \dfrac{n^2+1}{2m} 与 \sqrt{2^{n-1}+m+4} 都是正整数,试求 m,n 的值.(题目来源:2020 日本数学奥林匹克)
第七期:
31.$ 难度:$5
正数 a,b 满足 3a+b=14 ,试求:\dfrac{a^2}{a+2b}+\dfrac{b^2}{b+2} 的最小值.
32.$ 难度:$6
证明:不存在非负整数 k 和 m ,使得 k!+48=48(k+1)^m .
33.$ 难度:$5.5
设 P 为 圆 O 上任意一点。过 P 任意引 n 条直线 l_1,l_2,\cdots,l_n(n\ge2) ,第 i 条交圆于 M_{i},M_{i^{'}} 两点。若这 n 条直线中,任意相邻两条所成的角是 \dfrac{\pi}{n} ,求证:\sum\limits_{i=1}^n(|PM_i|^2+|PM_{i^{'}}|^2)=2nR^2 .
34.$ 难度:$5
35.$ 难度:$6
给定整数 n\ge3 ,记 f(n) 为满足以下条件的集合 A 的元素个数的最小值:
$(b)\space A$ 中不为 $1$ 的元素均为 $A$ 中另两个元素(可以相等)的和.
证明:$f(100)\ge108.
第八期:
$37.$ 难度:$0$ ~~温馨提示~~:有坑
解方程:$\arccos(\dfrac{4}{5})-\arccos(-\dfrac{4}{5})=\arcsin x.
(此题由于过于简单,笔者不写解答了。答案:{\color{white}\colorbox{white}{无解}} )
38.$ 难度:$6.5
设自然数 k 满足 1<k<100 ,对于 1,2,\cdots,100 的任意一个排列 a_1,a_2,\cdots,a_{100} ,取最小的 m>k ,使 a_m 至少小于 a_1,a_2,\cdots,a_k 中的 k-1 个数。已知满足 a_m=1 的数列个数为 \dfrac{100!}{4} ,试求 k 的值.
39. $ 难度:$6
数列 \{a_n\} 中,a_1=1 ,a_n=n^2\sum\limits_{i=1}^{n-1}\dfrac{1}{i^2}(n\ge2) 。求证:\prod\limits_{i=1}^n(1+\dfrac{1}{a_i})<4(n\ge1).
40.$ 难度:$5.5
已知 a,b,c,x,y,z\in\mathbb{R^+} ,求证:
\dfrac{x}{y+z}(b+c)+\dfrac{y}{z+x}(c+a)+\dfrac{z}{x+y}(a+b)\ge\sqrt{3(ab+bc+ca)}.
第九期:
41.$ 难度:$9
求所有函数 f:\mathbb{R\mapsto R} ,使得 f(1)=1 ,且对于任意实数 x,y(y\neq0) 都有:
f(yf(x)+\dfrac{x}{y})=xyf(x^2+y^2).
42.$ 难度:$8
若 z_i\in\mathbb{C}(i=1,2,3,4,5) ,|z_1|\le1,|z_2|\le1,|2z_3-(z_1+z_2)|\le|z_1-z_2|,|2z_4-(z_1+z_2)|\le|z_1-z_2|,|2z_5-(z_3+z_4)|\le|z_3-z_4| ,试求 |z_5|_{\max}.
43.$ 难度:$8.5
对于任意复数 z_1,z_2\cdots z_n ,设 \sigma_i 为关于这 n 个复数的 i 次对称式。(编者注:即关于 x 的方程 x^n-\sigma_1x^{n-1}+\sigma_2x^{n-2}-\cdots+(-1)^n\sigma_n 的 n 个根分别是 z_1,z_2,\cdots,z_n )\gamma ,使得对任意模不大于 1 的复数 z_1,z_2\cdots z_n ,都有 1+|\sigma_1|+|\sigma_2|+\cdots+|\sigma_n|\ge\gamma(|z_1|+|z_2|+\cdots+|z_n|).
44.$ 难度:$7.5
证明:任意连续 100 个正整数的乘积不是完全平方数.
45.$ 难度:$8
已知正整数 n_1<n_2<\cdots<n_k ,证明:P(z)=1+z^{n_1}+z^{n_2}+\cdots+z^{n_k}=0 在 |z|<\dfrac{\sqrt{5}-1}{2} 内没有根,其中 z\in\mathbb{C} .
第十期:
46.$ 难度:$6.5
若 p_1,p_2,\cdots p_n 是小于 2^{100} 的所有素数从小到大的排列,证明:S=\frac{1}{p_1}+\frac{1}{p_2}+\cdots+\frac{1}{p_n}<10.
(2005\ \text{Romania}$,十年级组决赛$)
47.$ 难度:$7
设奇数 n>1 ,求 \prod\limits_{k=1}^m\cos\dfrac{a_k\pi}{n}. 其中, a_1,a_2,\cdots,a_m 为所有不大于 n 且和 n 互质的正整数.
48.$ 难度:$8
给定正整数 n .对于 x_i\in[-1,1](i=1,2,\cdots,2n) ,求 \sum\limits_{1\le r<s\le 2n}(s-r-n)x_rx_s 的最大值.
49.$ 难度:$6.5
若 a_1=1,b_1=\tan\theta,a_n=a_{n-1}\cos\theta-b_{n-1}\sin\theta,b_n=a_{n-1}\sin\theta+b_{n-1}\cos\theta,\theta\in(0,\frac{\pi}{2}) ,
求 \{a_n\},\{b_n\} 的通项公式.
50.$ 难度:$7
给定正整数 N\ge4 ,证明:一定存在严格递增的正整数数列 \{a_n\}(n\ge1) ,使得对于任意正整数 n ,有
\dfrac{a_{2n-1}+a_{2n}}{a_n}=N.
第十一期
51.$ 难度:$8
设 p>3 为素数。证明:存在连续三个整数,它们都不是模 p 意义下的二次非剩余。
52,$ 难度:$7
Find the sum of all the positive solutions of
(2014\ AMC\ 12B,\ Problem\ 25)
53.$ 难度:$7.5
在一个 2018\times2018 的棋盘上放置着 2018 个不能互相攻击皇后,证明:存在两个皇后,她们的外接矩形(即皇后在对角线两端)的半周长为 2018 。
54.$ 难度:$8.5
$$\left(\sum\limits_{i=1}^n \frac{x_i}{i}\right)\left(\sum\limits_{i=1}^n ix_i\right)\le\frac{(n+1)^2}{4n}\left(\sum\limits_{i=1}^n x_i\right).$$
$55.$ 难度:$8
$$\sum\limits_{i=1}^n\frac{1}{n-1+x_i}\le 1.$$
------------
### 第十二期
$56.$ 难度:$5
设 n 个复数的模的和为 1 。证明:其中必存在若干个复数,它们的和的模不小于 \frac16.
57.$ 难度:$6
对于任意正整数 n ,证明:
\sin\frac{\pi}{4n}\sin\frac{3\pi}{4n}\cdots\sin\frac{(2n-1)\pi}{4n}=\frac{\sqrt2}{2^n}.
58.$ 难度:$7
$$\sum\limits_{i=1}^n\left(a_iS_i\sum\limits_{i=1}^n a_j^2\right)\le \sum\limits_{i=1}^n(a_iS_i)^2.$$
$59.$ 难度:$6.5
如图,\triangle ABC 的外心为 O ,BC 的中垂线交圆 O 于 M,N ,D,E 为 AB,AC 中点。设 OE 与 AN 交于 P ,证明:A,M,D,P 共圆。
60.$ 难度:$9
设正整数 a,b 满足:对于任意正整数 n ,有 s(an)=s(bn) ,其中 s(x) 表示正整数 x 在十进制下各位数字之和。证明:
\lg a-\lg b\in\mathbb{Z}.
第十一期:
61.$ 难度:$9
在\triangle ABC 内有一点 O ,CO\cap AB=D,BO\cap AC=E,AO\cap \odot(ABC)=F ,\odot(ABC) 在 B,C 处切线交于 G ,GF\cap \odot(ABC)=H ,H 关于 BC 对称点 I .
证明:\odot(ABC),\odot(ADE),\odot(OFI) 共点。
62.$ 难度:$6
设 a,b,c 为两两不等的正实数。证明:
\dfrac{ab+bc+ca}{(a+b)(b+c)(c+a)}<\dfrac17\left(\dfrac{1}{|a-b|}+\dfrac{1}{|b-c|}+\dfrac{1}{|c-a|}\right).
(2021 中国东南数学奥林匹克,十年级组,第二天第三题)
63.$ 难度:$5
在 \triangle ABC 中,证明:
\sum\sqrt{1-\sin A\sin B}\ge \frac 32.
64.$ 难度:$7
求所有正整数 n ,使得对任意与 n 互质的正整数 a ,有
2n^2\mid (a^n-1).
(2015 土耳其数学奥林匹克)
65.$ 难度:$9
将圆周上 1994 个点染 10 种颜色。已知任意相邻 100 个点中出现所有 10 种颜色,求证:存在相邻 90 个点中出现所有 10 种颜色。