树链剖分
CQ_Alice
·
·
个人记录
树结构大家不陌生,想必大家一定非常爱它!
所以我们说说树上的进阶操作!
树有个很好玩的地方,就是任意两点之间有且仅有一条最短路,我们把这条最短路称为两点的简单路径。那么我们对它的操作,无疑就是对两点之间的简单路径、一颗子树又或者同一深度的那些点那些边进行各种操作与维护。
显然,2022 年的计算机太垃了,一秒钟连 10^{10^9} 次都跑不到,这令我打题天天TLE的小朋友非常不爽,于是有一个叫轻重树链剖分的思想横空出世。
是谁提出这么一个不错思想的呢?我也不知道,网上似乎也查不到,但我觉得提出这个思想的人一定是在 OI 赛场上因不会倍增维护边权而TLE的小朋友,一怒之下,心想既然改变不了硬件设备,那我们就来对其进行升华,充分发挥我们的智慧!
于是呢,我们就来康康这个载千年 OI 之精华的算法是怎么操作的。
轻重链剖分
要知道,在序列中想要维护一段线性数据,可以用线段树等高端算法,不仅灵活性高,时间复杂的也够低。
但在树上,我们能考虑的也只有暴力了,似乎找不出什么办法能同时驾驭修改与查询
于是呢,我们考虑能不能将树的那些点或边变成一个线性数据,然后用线段树或树状数组等算法来维护他呢,答案是显然的,因为我们发现在树上的一系列操作,就好比对两点之间简单路径的修改,他所修改的点始终都是在一条链或多条链上,因此我们可不可以找到一种方式,将树剖分成若干条链,然后在由一条条链组成的线性数据上进行维护呢?那么接下来请走进轻重链剖分这个优美的思想。
如何对树进行剖分
由于要使剖分后的链一定能够包含到查询的点,所以我们考虑将链分成两种,重链 and 轻链。
重儿子:父亲节点的所有儿子中子树结点数量最多的结点;
轻儿子:父亲节点中除了重儿子以外的儿子;
重边:父亲结点和重儿子连成的边;
轻边:父亲节点和轻儿子连成的边;
重链:由连续多条重边连接而成的路径。
轻链:即轻边。
比如上面这幅图中,用黑线连接的结点都是重结点,其余均是轻结点。
由于我们对于每个点都会向下引出一条到底的重链,而轻链则可以**连接或到达各个重链**,因此我们一定可以将**任意**两点的路线分成**若干段**,并在**剖分出来**的链中找到并进行维护,所以轻重链剖分可行性证明!
随后又引出一个问题,既然要将路径分成若干段,如果每一段都$log$级别维护,那岂不是 TLE?
### 时间复杂度:
用 $Sizs_i$ 表示以 $i$ 为根的子树的节点数量。
先考虑轻链,如果 $U$ 是 $V$ 的父亲,并且它们之间以轻边连接,那么首先 $U$ 至少会存在两个儿子,这时点 $V$ 成为点 $U$ 的**轻儿子**,则意味着$U$的另外一个或多个儿子的$Size$值之和必定大于或等于 $V$ 的 $Size$ 值,因此存在 $Size_U ≥ Size_V *2 $,那么每向上走一步轻链就会令**子树节点数**$*=2$,因此从**任意一点**向上走到**树根**,所遇到的**轻链数量**不会超过 $log_n$。
那么再次基础上,重链就非常好考虑了:由于轻链**只有**$log$级别条,那么**重链**又可以看作用来**连接轻链**,因此从**任意一点**向上走到**树根**,所遇到的**重链数量**至多也是$log_n$条。
所以**每次维护**的时间复杂度为 $log_n*log_n$,一个 $log_n$ 是**维护线段树**的代价,另一个是指有 $log_n$ 条链需要用线段树维护。
### 实现
在我们理解了**树链剖分**的实现原理和证明后,我们就可以开始正式学习了。
#### 首先,如何实现分轻重链
我们需要求出一下几个数组:
$Size_i$:表示以点$i$做根的**子树**的**节点数量**。
$Son_i$:表示点$i$的**重儿子**。
$Dep_i$:表示点$i$的深度。
$F_i$:表示点$i$的父亲。
这些值**都**可以在**一次深搜**中求解完。
```cpp
void DFS_1( int X , int Fa ) {
F[X] = Fa ;
Size[X] = 1 ;
DEP[X] = DEP[Fa] + 1 ;
int Nax = 0 , L = - 1 ;
for(int i = Bo[X] ; i ; i = Tr[i].Ne ) { //链式前向星
int V = Tr[i].V ; if( V == Fa ) continue ; // V是X的儿子
DFS_1( V , X ) ; Size[X] += Size[V];
if(Size[V] > Nax) Nax = Size[V] , L = V ; //找所有儿子中子树结点数量最多的结点
} if(L != -1) Son[X] = L ;
}
```
接下来我们还需要求出一下几个数组:
$Ser_i$:表示在由链组成的**序列**中**下表**$i$所表示的**点的点权**。
$P_i$:表示点$i$映射到由链组成的**序列**中的**下表**。
$Top_i$:表示以点$i$所在的**链的起点**。
这些则值需要在第一步的**基础上**才能继续求解。
```cpp
void DFS_2( int X , int T , int F ) {
Top[X] = T ; // T表示点X所在的链的起点。
P[ X ] = S + 1 ; // S表示当前正在存储链数组的第几位
Ser[ ++ S ] = A[X] ; // 第 ++ S储存的是点X的值,A[X]表示点X的点权
if(Son[X] != -1) DFS_2( Son[ X ] , T , X ) ;//如果有重儿子就走,但重链起点是不变的
for(int i = Bo[X] ; i ; i = Tr[i].Next) {
int V = tree[i].V ; if(V == Son[X] || V == F) continue ;
DFS_2(V , V , X) ;//此时的V为U的轻儿子,对于点V所在的轻链起点变为点V本身
}
}
```
那么现在我们已经**剖分**好了这棵**树**,接下来则**需要**用线段树来**维护**(维护上面代码求出的$Ser$数组)
#### 线段树大家肯定都会写
所以我们就用这几个**函数**表示对**剖分数组**的**维护**。
$Fix(i,l,x):$表示将剖分数组的第$i$~$l$位加上$x$ ;
$Qun(i,l,x):$表示剖分数组的第$i$~$l$位的和 。
那么在写完了上面两个函数后,接下来就是真正对"**树**"的**操作**了。
------------
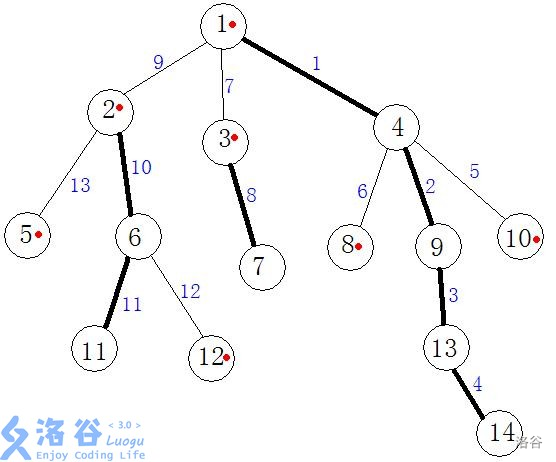
那么剖分后的**点序列**为$1,4,9,13,14,8,10,3,7,2,6,11,5,12
那么像12这个点就是点序列的最后一位。
对于上面的图,如果我们要修改12~8的简单路径,那么我们可以将其分成四个步骤对它进行修改。
第一步
我们看一下两点所在的链的起点谁的深度更大,那么我们就先去维护他。
例如上图中12所在链的起点是12,深度为4,这时8所在链的起点也是8,深度为3 , 4>3 , 那么我们就先走 12。
第二步
将点12 ~ Top_{12}的值进行修改,即对剖分序列的P_{Top_{12}} ~ P_{12}进行修改,即Fix( P_{Top_{12}} , P_{12} , x) ,一条链上深度更低的点一定比深度更大的点先入序列,所以注意修改的左右端点不要搞反了。
第三步
在我们将12这个点走完后,我们则需要让12点向上跳以助于下一步操作,所以点12来到点F_{Top_{12}}。
第四步
在上述三步不断地进行后,两个点最后一定会来到一条链上,如下图 :
此时X和Y处于同一条链上,那么此时我们则需要特殊考虑对点X~点Y的路径进行修改,因此我们需要先按照X,Y的深度大小进行修改,例如X的深度比Y小,那么就Fix( P[X] , P[Y] , x) 。
剖分点序列为1,4,9,12,14,8,10,3,7,2,6,11,5,12
那么我么来模拟一遍两点的跳动情况对点序列的修改:
初始状态 : X = 12 , Y = 8,此时没有修改
$No.2 : $ $X = 6 , Y = 4$ , 此时修改点序列中下标$6$ ~ $6$这些**点的权值** ;
$No.3 : $ $X = 1 , Y = 4$ , 此时修改点序列中下标$10$ ~ $11$这些**点的权值** ;
$No.4 : $ $X = 1 , Y = 4$ , 此时修改点序列中下标$1$ ~ $2$这些**点的权值** ;
第四步**结束后**完成**修改**。
```cpp
void Fix_Tr( int X , int Y , int Z ) {//将X到Y的简单路径的每一个点+Z
while( Top[X] != Top[Y] ) {
if( Dep[Top[X]] < Dep[Top[Y]] ) swap( X , Y ) ;
Fix(P[Top[X]],P[X],Z); // 修改一条链
X = F[Top[X]] ;//往上跳
}
if( Dep[X] < Dep[Y] ) swap( X , Y ) ;
Fix(P[Y] , P[X] , Z ) ;
}
```
#### 查询同理
```cpp
void Fix_Tr( int X , int Y ) {//将X到Y的简单路径点权和
int Ans = 0 ;
while( Top[X] != Top[Y] ) {
if( Dep[Top[X]] < Dep[Top[Y]] ) swap( X , Y ) ;
Ans += Qun(P[Top[X]],P[X]); // 修改一条链
X = F[Top[X]] ;//往上跳
}
if( Dep[X] < Dep[Y] ) swap( X , Y ) ;
Ans += Fix(P[Y] , P[X]) ;
return Ans ;
}
```
### 修改子树
我们**剖分树**的过程中,由于采用的是**深搜**,因此在**点序列**中,**任意**一点的**后面**一定会**连续不中断**的进入其的**子树节点**,因此点$x$的子树一定会在点序列的$P_X$~$(P_X+Size_x)$这段区间,因此直接一次线段树维护即可。
```cpp
void Fix_Shu( int X , int Z ) {//将X为根的子树+Z
Fix( P[X] , P[X] + Size[X] , Z ) ;
}
int Qun_Shu( int X , int Z ) {//查询X为根的子树点权和
return Qun( P[X] , P[X] + Size[X] ) ;
}
```
##### 嗯,看来你已经学懂了树链剖分,那快去做题吧!
[P3384](https://www.luogu.com.cn/problem/P3384)
[P2590](https://www.luogu.com.cn/problem/P2590)
[P3178](https://www.luogu.com.cn/problem/P3178)
祝大家早日$AK IOI!