树的重心
samaofCaCa
·
·
个人记录
定义
一棵树以x为根时,其最大子树的结点数最小则x为这棵树的根。
求法
# 性质
## 1,树的重心的最大子树大小$\le n/2$。若一个点为根的最大子树$\le n/2$,则这个点也必然是树的重心。
证明:若一个点为根的最大子树$\ge n/2$,可以使它重边连接的儿子作根,其最大子树便会变小,直至所有的子树大小$\le n/2$。第一部分得证。
若一个点为根的最大子树$\le n/2$,以任一另外的结点为根,其最大子树大小$\ge n/2$,取等号的情况为有两个重心。所以此结点必为树的重心。
## 2,树的重心最多只有两个,且相邻。
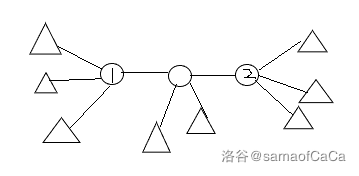
证明:当树的重心有多个或不相邻时,两个重心的链中有别的结点。如图,设重心与其三角形子树的结点数和为$tot$,重心的最大子树的结点数为$max$,中间部分的结点数为$mid$。
1,当结点1的最大子树为左边的三角形。
若结点2的最大子树为右边的三角形,由于$max_1\ge mid+tot_2$,那么$max_1>max_2$,与结点2为树的重心矛盾。
若结点2的最大子树$max_2=tot_1+mid$,那么$max_1<max_2$,与结点1为树的重心矛盾。
2,当结点1的最大子树$max_1=mid+tot_2$,由于结点1和结点2都是重心,$max_1=max_2$,那么$max_2$只能为$mid+tot_1$,$max_1=max_2$,那么中间的圆点的最大子树为$max(tot_1,mid-1)<max_1=max_2$。与结点1,结点2为树的重心矛盾。
证毕。
## 3,所有点到某个点的距离和中,到树的重心的距离和是最小的。若有两个重心他们的距离和一样。
证明:把树的重心作为根,设距离和为$ans$,以$x$为根的子树结点数为$cnt_x$。取别的点为求和点时,距离和为$ans-cnt_x+(n-cnt_x)$。有性质1可知$cnt_x\le n/2$。所以$ans-cnt_x+(n-cnt_x)\ge ans$。取等号的情况为$cnt_x=n/2$,此时$x$为另一个树的重心。
## 4,两棵树通过一条边相连,新的树的重心在原来两棵树的重心的连线上。
证明:设两棵树的结点数分别为$n_1$,$n_2$。对于不在两棵树的重心连线上的点,其最大子树$\ge n_1/2+n_2$或$n_2/2+n_1$即$\ge (n_1+n_2)/2$。不可能为新的树的重心。
## 5,一棵树添加或删除一个点,树的重心最多只移动一条边的位置。
证明:以重心为根,添加一个点时,当重心移动,当且仅当其其中一棵子树$x\le n/2$且$x+1>(n+1)/2$,可推出$x=n/2$。往该子树移动一条边时,最大子树为$n/2=\lfloor (n+1)/2 \rfloor$,所以该点为树的重心。
任意一棵树$x$添加一个点后变为$y$,重心最多移动一条边的位置。
所以$y$删除一个点后变为$x$,重心也最多移动一条边的位置。
证毕。