组合数学
bloodstalk
·
2022-10-07 18:34:01
·
个人记录
前置知识
加法原理
若完成一件事的方法有 n 类i 类方法有 a_i 种不同的方法,且这些方法互不重合,那么完成这件事共有 a_1 + a_2 + \dots + a_n 种方法。
乘法原理
若完成一件事需要 n 个步骤i 个步骤有 a_i 种不同的方法,且这些步骤互不干扰,则完成这件事共有 a_1 \times a_2 \times \dots \times a_n 种方法。
于我的观点,加法原理适用于一个问题的不同解,而乘法原理就是把一个问题不同步骤的不同解乘起来了。
抽屉原理
把 n+1 个元素划分至 n 个集合 A_1,A_2,\dots,A_n 中,则至少存在一个集合 A_i ,使得 A_i 这个集合中的元素个数 \ge 2 。
没错,这就是抽屉原理,也叫鸽巢原理。
我们拓展一下。
把 nm+1 个元素划分至 n 个集合 A_1,\dots,A_n 中,则至少存在一个集合 A_i ,使得 A_i 这个集合中的元素个数 \ge m+1 。
更普遍地。
把 m(\ge n) 个元素划分至 n 个集合 A_1,\dots,A_n 中,则至少存在一个集合 A_i ,使得 A_i 这个集合中的元素个数 \ge \lfloor \frac{m}{n} \rfloor 。
容斥原理
在计数时,必须注意没有重复,没有遗漏。为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。
集合的并
设 U 中元素有 n 种不同的属性,第 i 种属性称为 P_i ,拥有属性 P_i 的元素构成集合 S_i ,那么
\Bigg|\bigcup_{i=1}^nS_i\Bigg|=\sum_i|S_i|-\sum_{i<j}|S_i\cap S_j|+\sum_{i<j<k}|S_i\cap S_j \cap S_k|-\dots
+(-1)^{m-1}\sum_{a_i<a_{i+1}}\Bigg|\bigcap_{i=1}^mS_{a_i}\Bigg|+\dots+(-1)^{n-1}|S_1\cap\dots\cap S_n|
即
\Bigg|\bigcup_{i=1}^nS_i\Bigg|=\sum_{m=1}^n (-1)^{m-1}\sum_{a_i<a_{i+1}}\Bigg|\bigcap_{i=1}^mS_{a_i}\Bigg|
意义:集合的并 等于集合的交的交错和 (奇正偶负)。
集合的交
集合的交 等于全集 减去补集的并 。
\Bigg|\bigcap_{i=1}^nS_i\Bigg|=|U|-\Bigg|\bigcup_{i=1}^n\overline{S_i}\Bigg|
右边补集的并容易用容斥原理求解,这就求出了集合的交。
排列组合
排列
定义
从 n 个不同元素中依次取出 m 个元素排成一列,产生的不同排列 的数量。((1,2) 和(2,1) 算两种方案),记作A_n^m(m \leq n)
A_n^1$ 等于从 $n$ 个数中选 $1$ 个数的方法总数,显然 $A_n^1 = n
A_n^2$ 等于从 $n$ 个数中选 $2$ 个数的方法总数。我们可以分两步处理:第一步,选一个数放在第一个位置,有 $n$ 种选法;第二步,选一个数放在第二个位置,因为已经用了一个了,所以还有 $n-1$ 个数,因此有 $n-1$ 种选法。根据乘法原理,一共有 $n(n-1)$ 种选法,因此 $A_n^2 = n(n-1)
类似的,我们可以知道
A_n^3 = n(n-1)(n-2)
A_n^4 = n(n-1)(n-2)(n-3)
一般的,我们可以得到它的通项公式:
A_n^m = \underbrace{n(n-1)(n-2)\dots (n-(m-1))}_{m\text{项}}
用一种更简便的方法来表示
A_n^m = n(n-1)(n-2)\dots (n-(m-1))
= \frac{n(n-1)(n-2)\dots (n-(m-1)) \times (n-m)\times \dots .\times 1}{(n-m)\times \dots .\times 1}
= \frac{n!}{(n-m)!}
为了保证 n=m 的时候也有解,我们规定 0! = 1 。
性质
nA_{n-1}^{m-1} = A_n^m
证明:
nA_{n-1}^{m-1} = \frac{(n-1)!\times n}{(n-1 - (m-1))!}
= \frac{n!}{(n-m)!} = A_n^m
mA_{n-1}^{m-1} + A_{n-1}^m = A_n^m
证明:
mA_{n-1}^{m-1} + A_{n-1}^m = \frac{m(n-1)!}{(n-m)!} + \frac{(n-1)!}{(n-m-1)!}
= \frac{m(n-1)! + (n-m)(n-1)!}{(n-m)!}
= \frac{n!}{(n-m)!} = A_n^m
组合
定义
从 n 个不同元素中选 m 个组成一个集合,产生的不同集合的数量。(不考虑顺序,(1,2) 和(2,1) 算一种)
由此我们推出组合的通项公式:
$$
C_n^m = \frac{A_n^m}{A_m^m} = \frac{\frac{n!}{(n-m)!}}{m!} = \frac{n!}{m!(n-m)!}
$$
### 性质
1.
$$
C_n^m = C_{n-1}^{m-1} + C_{n-1}^{m}
$$
证明:从 $n$ 个数选 $m$ 个数,就等于选了第一个数,再从 $n-1$ 个数中选 $m-1$ 个数,和不选第一个数,从 $n-1$ 个数中选 $m$ 个的方案数总和。
这个其实看杨辉三角能很轻松的看出来,杨辉三角的第 $n$ 行的第 $m$ 列对应的数就是 $C_n^m
2.
C_n^m = C_n^{n-m}
证明:
C_n^{n-m} = \frac{n!}{[n-(n-m)]!(n-m)!}
= \frac{n!}{m!(n-m)!} = C_n^m
感性理解,你每次从 n 个物品中选 m 个物品,那么必然剩下 n-m 个物品,每种选取 n 个物品的方案和选取剩下的 n-m 个物品的方案是一一对应的。
3.
C_{n+m+1}^{m} = \sum_{i=0}^mC_{n+i}^i
证明:首先对性质 1 变形:C_n^m + C_n^{m-1}=C_{n+1}^{m} ,并且我们知道 C_n^0 = C_{n+1}^0 = 1 , 那么就有
\sum_{i=0}^mC_{n+i}^i = C_n^0 + C_{n+1}^1 + \dots + C_{n+m}^m
替换第一项
= C_{n+1}^0 + C_{n+1}^1 + \dots + C_{n+m}^m
合并
= C_{n+2}^1 + C_{n+2}^2 + \dots + C_{n+m}^m
以此类推
= C_{n+m+1}^m
4.
C_n^m \cdot C_m^r =C_n^r \cdot C_{n-r}^{m-r}
证明:
C_n^m \cdot C_m^r = \frac{n!}{m!(n-m)!}\cdot \frac{m!}{r!(m-r)!}
= \frac{n!}{r!(n-m)!(m-r)!}
分子分母同乘(n-r)!
= \frac{n!}{r!(n-r)!}\cdot \frac{(n-r)!}{(m-r)!(n-m)!} = C_n^r \cdot C_{n-r}^{m-r}
运用组合的思想理解一下,左边就是先从 n 个中选 m 个,再从 m 个选 r 个的方案数。
这就等价于右边先从 n 个中选 r 个,再从剩下的 n-r 个中选没被选上的 m-r 个。
5.
m \cdot C_n^m = n \cdot C_{n-1}^{m-1}
证明:由性质 4 得
m \cdot C_n^m = C_m^1 \cdot C_n^m
= C_n^1 \cdot C_{n-1}^{m-1} = n \cdot C_{n-1}^{m-1}
6.二项式定理的特殊形式
\sum_{i=0}^nC_n^i\cdot x^i = (x+1)^n
\Rightarrow
C_{n}^{0} + C_{n}^{1} + C_{n}^{m} + \dots + C_{n}^{n} = \sum_{i=0}^nC_n^i = 2^n
证明:取 x=1 ,即有 \sum_{i=0}^nC_n^i = 2^n , 至于二项式定理,一会再说明。也可以从另一个方面去想, 从 n 个元素中取出若干个元素组成一个集合,有 n+1 类方法,分别是取出 0,1,2,\dots,n+1 个,根据加法原理,共有 C_n^0 + C_n^1 + \dots +C_n^n 种方法;又根据乘法原理,每个数可以选或不选,所以一共有 2^n 种方法。二者相等,所以公式成立。
7.
\sum_{i=0}^n(-1)^iC_n^i = 0
证明:当 m 为奇数时,由性质 2 可得,两项一一对应和为 0 ,显然成立;当 m 为偶数时,利用 C_n^0 = C_{n-1}^0 , C_m^m = C_{m-1}^{m-1} 替换,再用递推式得到
\sum_{i=0}^n(-1)^iC_n^i = C_n^0 - C_n^1 + C_n^2 - \dots -C_n^{n-1} +C_n^n
= C_{n-1}^0 - C_n^1 + \dots - C_n^{n-1}+C_{n-1}^{n-1}
= C_{n-1}^0 - (C_{n-1}^0 + C_{n-1}^1) + \dots - (C_{n-1}^{n-2} + C_{n-1}^{n-1}) + C_{n-1}^{n-1} = 0
C_n^0 + C_n^2 + C_n^4 + \dots =C_n^1 + C_n^3 + C_n^5 + \dots = 2^{n-1}
证明:由性质 7 显然可得。
C_{n+m}^{r} = \sum_{i=0}^r C_n^iC_m^{r-i}
证明:在 (n+m) 个数中选 r 个数,在前 n 中选 i 个数的方案有 C_n^i 种,在后 m 个里选 (r-i) 个数的方案有 C_m^{r-i} 种,相乘并求和即可得到该式。
\sum_{i=0}^n(C_n^i)^2 = C_{2n}^n
证明:由性质 9 取 m=n 即可得。
\sum_{i=1}^nC_n^i \cdot i = \sum_{i=0}^n C_n^i \cdot i = n\cdot 2^{n-1}
证明:把左边展开得
\sum_{i=1}^nC_n^i \cdot i = \sum_{i=1}^n\frac{n!}{(n-i)!(i-1)!}
= n \cdot \sum_{i=1}^n\frac{(n-1)!}{(n-i)!(i-1)!}
= n \cdot \sum_{i=1}^{n}C_{n-1}^{i-1}
= n \cdot \sum_{i=0}^{n-1} C_{n-1}^i = n \cdot 2 ^{n-1}
\sum_{i=1}^nC_n^i \cdot i^2 = \sum_{i=0}^n C_n^i \cdot i^2 = n(n+1)\cdot 2^{n-2}
证明:类似于11
\sum_{i=1}^nC_n^i \cdot i^2 = \sum_{i=1}^n\frac{n!\cdot i}{(n-i)!(i-1)!}
把 i 拆成 i-1 和 1
= n \cdot \sum_{i=1}^n\frac{(n-1)!}{(n-i)!(i-1)!} + n \cdot \sum_{i=1}^n\frac{(n-1)!(i-1)}{(n-i)!(i-1)!}
= n2^{n-1} + n\cdot \sum_{i=1}^{n}C_{n-1}^{i-1}(i-1)
由性质5(m \cdot C_n^m = n \cdot C_{n-1}^{m-1})
= n2^{n-1} + n \cdot (n-1) \cdot \sum_{i=2}^{n} C_{n-2}^{i-2}
= n2^{n-1} + n \cdot (n-1) \cdot 2^{n-2}
= 2n \cdot 2^{n-2} + n \cdot(n-1) \cdot 2^{n-2} = n(n+1)\cdot2^{n-2}
组合数取模
C_n^m \ \text{mod} \ p
当然也可以 $O(n\log n)$ 预处理 $i!$ 和 $i!$ 的逆元,询问的时候 $O(1)$ 的 `ans = jc[n] * inv[m] * inv[n-m] % p` 即可。
若要对 C_n^m 进行高精度计算。有类似于阶乘分解那一题的计数原理,计算出每个质因子的个数,然后上减下,把分母消去,最后剩下的质因子乘起来,就能得到答案。
若 p 为质数,1 \leq n,m \leq 10^9 , p \leq 10^5 : 应用卢卡斯定理,将 n,m 转化为 p 进制数。一会细讲。
后言
还有一些常见的方法,具体见高中数学瞎记
二项式定理
(x+y)^n = \sum_{k=0}^{n}C_n^kx^{n-k}y^k
感性证明:
(x+y)^n
也就是
\underbrace{(x+y)\cdot(x+y)\cdot(x+y)\cdot\dots\cdot (x+y)}_{n\text{项}}
如果每个 (x+y) 出来的都是 x ,那么就是 x^ny^0 ,如果出来了 n-1 个 x ,1 个 y ,那么就是 x^{n-1}y^0 ,那么总共就是 x^ny^0 + x^{n-1}y^1 + \dots + x^1y^{n-1}+x^0y^n 这样一个形式。
接下来考虑系数。从n 个 (x+y) 中选 0 个 y ,显然方案数就是 C_n^0 ;同理,选一个 y 就是 C_n^1 ,因为选 x 跟选 y 的方案是一一对应的。所以最后的系数就是
C_n^0x^ny^0 + C_n^1x^{n-1}y^1 + \dots + C_n^{n-1}x^1y^{n-1}+C_n^nx^0y^n
的形式,写成通项公式就是
(x+y)^n = \sum_{k=0}^{n}C_n^kx^{n-k}y^k
其中 C_n^k 就被称为二项式系数 。
拓展一下, (ax+by)^n 就是
(ax+by)^n = \sum_{k=0}^{n}C_n^ka^{n-k}x^{n-k}b^ky^k
所以 x^{n-k}y^k 的系数就是 C_n^ka^{n-k}b^k ,而它的二项式系数还是 C_n^k 。
多重集
多重集的排列组合
多重集就是有重复元素的广义的,不满足互异性的集合。也就是 multiset。
寄,来不及学了,不学了。
给两个公式得了。
多重集的排列数
设 S = \{n_1 \times a_1,n_2 \times a_2,\dots ,n_k\times a_k\} 是由 n_1 个 a_1 ,n_2 个 a_2\dots ,n_k 个 a_k 组成的多重集,记 n = n_1 + n_2 + \dots +n_k 。 S 的全排列个数为
\frac{n!}{n_1!n_2!\dots n_k!}
多重集的组合数
设 S = \{n_1 \times a_1,n_2 \times a_2,\dots ,n_k\times a_k\} 是由 n_1 个 a_1 ,n_2 个 a_2\dots ,n_k 个 a_k 组成的多重集,记 n = n_1 + n_2 + \dots +n_k 。
设整数 r \leq n_i(\forall i \in [1,k]) 。从 S 中取出 r 个元素组成一个多重集(不考虑元素的顺序),产生的不同多重集的数量为 C_{k+r-1}^{k-1} 。
Lucas 定理
适用情形
如上文所述,如果遇到 n 和 m 都很大的组合数取模问题,其中 1\leq m\leq n\le10^{18},1\leq q \leq 10^5 ,并且保证 p 为质数的时候,就可以使用 Lucas 定理了。
内容
C_n^m \equiv C_{n/p}^{m/p}C_{n \ \text{mod} \ p}^{m \ \text{mod} \ p}(\text{mod} \ p)
证明
引理 1 :C_p^x \equiv 0(\text{mod} \ p) , 0 < x < p
因为
C_p^x = \frac{p!}{x!(p-x)!} = \frac{p(p-1)!}{x(x-1)!(p-x)!} = \frac{p}{x}C_{p-1}^{x-1}
则有
C_p^x = p \cdot inv(x) C_{p-1}^{x-1} \equiv 0(\text{mod} \ p)
其中 inv(x) 表示 x 在模 p 意义下的逆元,因为 p 为质数且 x<p ,所以逆元一定存在。
引理 2 :(1+x)^p \equiv 1 + x^p(\text{mod} \ p)
由二项式定理得 (1+x)^p = \sum_{i=0}^p C_p^ix^i 。由引理 1 能得到,除了 i=0 ,i = p 两项,其余模 p 都是 0 , 而 i=0 这一项就是 C_p^0x^0 = 1 \equiv 1(\text{mod} \ p) ,i=p 这一项是 C_p^px^p = x^p \equiv x^p(\text{mod} \ p) ,加上那些中间模 p 等于 0 的项,就是 (1+x)^p \equiv 1 + x^p(\text{mod} \ p)
真正的证明:
令 n = ap + b , m = cp + d
$(1+x)^n = (1+x)^{ap+b} = ((1+x)^p)^a\cdot (1+x)^b
\equiv (1 + x^p)^a \cdot (1+x)^b = \sum_{i=0}^a C_a^ix^{ip} \cdot \sum_{j=0}^b C_b^jx^j(\text{mod} \ p)
这是式子 2 。
式子 1 中 x^m 这一项的系数是 C_n^m
式子 2 中 x^m = x^{cp}x^d 的系数为 C_a^cC_b^d
所以就有 C_n^m \equiv C_a^cC_b^d(\text{mod} \ p)
即
C_n^m \equiv C_{n/p}^{m/p}C_{n \ \text{mod} \ p}^{m \ \text{mod} \ p}(\text{mod} \ p)
Catalan 数列(卡特兰数)
定义
给定 n 个 0 和 n 个 1 ,它们随机排成长度为 2n 的序列,满足任意前缀 0 的个数都不少于 1 的个数的序列的数量为
Cat_n = C_{2n}^n - C_{2n}^{n-1} = \frac{C_{2n}^n}{n+1}
证明:
令 n 个 0 和 n 个 1 随机排成一个 2n 的序列 S ,如果说 S 不满足任意前缀中 0 的个数都不少于 1 的个数,那么一定存在一个最小的位置 2p+1 \in [1,2n] ,使得 S[1\sim 2p+1] 有 p 个 0 , p+1 个 1 。再把 S[2p+2\sim 2n] 的所有数字取反(0 变 1 ,1 变 0 )后,包含 n-p-1 个 0 和 n-p 个 1 ,于是我们得到了一个由 n-1 个 0 ,n+1 个 1 组成的序列。
同理,令 n-1 个 0 和 n+1 个 1 随机排成一个序列 S' ,那么一定存在一个最小的位置 2p'+1 \in [1,2n] ,使得 S'[1\sim 2p'+1] 有 p' 个 0 , p'+1 个 1 。再把 S[2p'+2\sim 2n] 的所有数字取反后,就得到了一个由 n 个 0 ,n 个 1 组成的,至少存在一个前缀 0 比 1 多的序列。
斯特林数
前置知识
圆排列
定义 :n 个不同元素围成一圈的个数,叫做圆排列数,记作 Q_n^n 。
计算公式 :
考虑其中已经排好的一圈,n 个元素之间有 n 个空,我们从这不同的 n 个空断开,每个空断开后形成了不同的线排列,总共 n 种。
这就说明圆排列是把 n 种线排列整合成 1 种了,于是我们得到圆排列的计算公式:
Q_n^n \times n = A_n^n
Q_n^n = \frac{A_n^n}{n}=(n-1)!
例如,3 个不同元素的圆排列数为 (3-1)!=2 种。
\text{from} \ 董晓算法
我们发现每个圆排列断开后形成 n 个线排列,这也就是我们计算公式的来源。
另一个公式 :
从 n 个不同元素中,选 m 个元素围成一圈的圆排列数,记作 Q_n^m ,那么就有
Q_n^m = C_n^mQ_m^m = \frac{n!}{m(n-m)!}
错位排列
定义 :错位排列是指没有任何元素出现在其有序位置的排列,对于 1\sim n 的排列 P ,如果满足 P_i \not=i ,则称 P 是 n 的错位排列。
错位排列数 :表示元素个数为 n 的错位排列个数,记作 D_n 。
$D_2 = 1$,即 $\{2,1\}$;
$D_3 = 2$,即 $\{2,3,1\},\{3,1,2\}$。
以此类推。
**递推公式**:
$$
D_n = (n-1)(D_{n-1}+D_{n-2})
$$
考虑如何递推,我们把它放在一个实际情况中进行理解。
假设我们有 $n$ 封信,编号 $1\sim n$,现在我们把这 $n$ 封信放在编号是 $1\sim n$ 的信封中,要求信封的编号与信的编号不一样。问有多少种不同的方法。
考虑第 $n$ 个信封,我们暂时把第 $n$ 封信放在第 $n$ 个信封中,然后考虑哪些情况能通过**一次操作**就变成 $n$ 位错排。
**情况 $1$** :前面 $n-1$ 个信封全部装错,那么第 $n$ 封只需要与前面 $n-1$ 个位置的信封交换即可,这样就有 $(n-1)D_{n-1}$ 种方法。
**情况 $2$** :前面 $n-1$ 个信封中有一个没装错其余的都装错了,那么第 $n$ 封只需要和那个没装错的交换就行了,没装错的信封有 $n-1$ 种可能,每种可能的其余 $n-2$ 封信是错排的,所以总共就是 $(n-1)D_{n-2}$ 种情况。
分类加法加起来,我们便得到了
$$
D_n = (n-1)(D_{n-1}+D_{n-2})
$$
## 第一类斯特林数(斯特林轮换数)
### 定义
将 $n$ 个不同元素,划分为 $m$ 个**非空圆排列**的方案数,记作 $\begin{bmatrix}n\\m\end{bmatrix}$。
### 递推公式
$$
\begin{bmatrix}n\\m\end{bmatrix} = \begin{bmatrix}n-1\\m-1\end{bmatrix}+(n-1)\begin{bmatrix}n-1\\m\end{bmatrix}
$$
放到实际情况下证明一下。
实际意义可以是 $n$ 个人坐 $m$ 张圆桌并且没有空圆桌的方案数。
考虑第 $n$ 个人座位的情况:
1. 若单独坐一桌,前面的 $n-1$ 个人就要坐到 $m-1$ 张桌子上,方案数就是 $\begin{bmatrix}n-1\\m-1\end{bmatrix}$;
2. 若坐到已经有人的桌子上,就先让前 $n-1$ 个人坐 $m$ 张桌子上,第 $n$ 个人可以坐到之前 $n-1$ 个人中任意一个人的左边,不重不漏,这样的方案数就是 $(n-1)\begin{bmatrix}n-1\\m\end{bmatrix}$。
分类加法,最后的方案数就是
$$
\begin{bmatrix}n\\m\end{bmatrix} = \begin{bmatrix}n-1\\m-1\end{bmatrix}+(n-1)\begin{bmatrix}n-1\\m\end{bmatrix}
$$
### 性质
$$
n! = \sum_{i=0}^n\begin{bmatrix}n\\i\end{bmatrix}
$$
每种排列都会对应着唯一一种置换。
## 第二类斯特林数(斯特林子集数)
### 定义
将 $n$ 个不同元素,划分为 $m$ 个**非空子集**的方案数,记作 $\begin{Bmatrix}n\\m\end{Bmatrix}$。
### 递推公式
$$
\begin{Bmatrix}n\\m\end{Bmatrix} = \begin{Bmatrix}n-1\\m-1\end{Bmatrix}+m\begin{Bmatrix}n-1\\m\end{Bmatrix}
$$
还是放到实际情况下证明一下。
实际意义可以是 $n$ 个人进 $m$ 个房间并且没有房间是空的的方案数,这里人不同而房间是相同的。
考虑第 $n$ 进房间的情况:
1. 若单独进一个房间,前面的 $n-1$ 个人就要进 $m-1$ 个房间里,方案数就是 $\begin{Bmatrix}n-1\\m-1\end{Bmatrix}$;
2. 若进已经有人的房间里,就先让前 $n-1$ 个人进 $m$ 个房间里,第 $n$ 个人可以进 $m$ 个房间中任意一个房间,不重不漏,这样的方案数就是 $m\begin{Bmatrix}n-1\\m\end{Bmatrix}$。
分类加法,最后的方案数就是
$$
\begin{Bmatrix}n\\m\end{Bmatrix} = \begin{Bmatrix}n-1\\m-1\end{Bmatrix}+m\begin{Bmatrix}n-1\\m\end{Bmatrix}
$$
## 斯特林反演
直接给出式子
$$
F(n) = \sum_{i=0}^n\begin{Bmatrix}n\\i\end{Bmatrix}G(i) \Longleftrightarrow G(n) = \sum_{i=0}^n(-1)^{n-i}\begin{bmatrix}n\\i\end{bmatrix}F(i)
$$
证明不会,略。
还有两个反转公式
$$
\sum_{k=m}^n(-1)^{n-k}\begin{bmatrix}n\\k\end{bmatrix}\begin{Bmatrix}k\\m\end{Bmatrix} = [m=n]
$$
$$
\sum_{k=m}^n(-1)^{n-k}\begin{Bmatrix}n\\k\end{Bmatrix}\begin{bmatrix}k\\m\end{bmatrix} = [m=n]
$$
这个公式运用最多的就是普通幂和上升幂下降幂的转换。
**下降幂**
$$
x^{\underline{k}} = x(x-1)\dots(x-k+1)=\frac{x!}{(x-k)!}=\frac{x!k!}{(x-k)!k!}=\binom{x}{k}k!
$$
**上升幂**
$$
x^{\overline{k}} = x(x+1)\dots(x+k-1)=\frac{(x+k-1)!}{(x-1)!}=\frac{(x+k-1)!k!}{(x-1)!k!}=\binom{x+k-1}{k}k!
$$
### 普通幂转下降幂
$$
x^n = \sum_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}x^{\underline{k}}=\sum_{k=0}^n\binom{x}{k}\begin{Bmatrix}n\\k\end{Bmatrix}k!
$$
也就是说,**第二类斯特林数**是**普通幂**展开成**下降幂**的系数。
---
我们从组合的思想证明一下:
左边是将 $n$ 个**不同**球放在 $x$ 个**不同**盒子里,每个球有 $x$ 种放法,所以共有 $x^n$ 种方法。
而右边枚举**非空**盒子的个数 $k$,从 $x$个盒子中选出 $k$ 个盒子,将 $n$ 个球放在这 $k$ 个盒子里,每个盒子不能为空,显然方案数就是第二类斯特林数。并且因为 $k$ 个盒子互不相同,所以还要对这 $k$ 个盒子进行一个全排列。
证毕。
-----
我们还可以用数学归纳法加以证明,首先列两个要用到的式子。
1.
$$
\begin{Bmatrix}n\\k\end{Bmatrix} = \begin{Bmatrix}n-1\\k-1\end{Bmatrix}+k\begin{Bmatrix}n-1\\k\end{Bmatrix}
$$
2.
$$
x^{\underline{k+1}}=x^{\underline{k}}(x-k)=x\cdot x^{\underline{k}}-k\cdot x^{\underline{k}}
$$
证明:
首先对于 $n=0,1$ ,式子显然成立。
当 $n>1$ 时,
$$
x^n = x\cdot x^{n-1}=x\sum_{k=0}^{n-1}\begin{Bmatrix}n-1\\k\end{Bmatrix}x^{\underline{k}}
$$
因为当 $k=n$ 时右边这个式子为 $0$,所以我们更改一下 $\sum$ 的上界。接着把 $x$ 放进去,运用式子 $2$:
$$
\begin{aligned}
&=x\sum_{k=0}^n\begin{Bmatrix}n-1\\k\end{Bmatrix}x^{\underline{k}}\\
&=\sum_{k=0}^n\begin{Bmatrix}n-1\\k\end{Bmatrix}x^{\underline{k+1}}+\sum_{k=0}^n\begin{Bmatrix}n-1\\k\end{Bmatrix}kx^{\underline{k}}\\
&=\sum_{k=1}^n\begin{Bmatrix}n-1\\k-1\end{Bmatrix}x^{\underline{k}}+\sum_{k=1}^n\begin{Bmatrix}n-1\\k\end{Bmatrix}x^{\underline{k}}\\
&=\sum_{k=1}^n\Bigg(\begin{Bmatrix}n-1\\k-1\end{Bmatrix}+k\begin{Bmatrix}n-1\\k\end{Bmatrix}\Bigg)x^{\underline{k}}\\
&=\sum_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}x^{\underline{k}}
\end{aligned}
$$
其中 $k$ 下界的变化是因为当 $k=n$ 时无意义,因此等效。
### 下降幂转普通幂
$$
x^{\underline{n}}=\sum_{k=0}^n\begin{bmatrix}n\\k\end{bmatrix}(-1)^{n-k}x^k
$$
我们同样使用归纳法证明,并且同样再列两个要用到的式子。
1.
$$
\begin{bmatrix}n\\k\end{bmatrix} = \begin{bmatrix}n-1\\k-1\end{bmatrix}+(n-1)\begin{bmatrix}n-1\\k\end{bmatrix}
$$
2.
$$
x^{\underline{n}} = x^{\underline{n-1}}(x-n+1)
$$
证明:
首先当 $n=0,1$ 时,式子成立。
当 $n>1$ 时,
$$
x^{\underline{n}} = x^{\underline{n-1}}(x-n+1)
$$
$$
\begin{aligned}
&=\sum_{k=0}^n\begin{bmatrix}n-1\\k\end{bmatrix}(-1)^{n-k-1}x^k(x-n+1)\\
&=\sum_{k=0}^n\begin{bmatrix}n-1\\k\end{bmatrix}(-1)^{n-k-1}x^{k+1}-\sum_{k=0}^n\begin{bmatrix}n-1\\k\end{bmatrix}(-1)^{n-k-1}x^k(n-1)\\
&=\sum_{k=1}^n\begin{bmatrix}n-1\\k-1\end{bmatrix}(-1)^{n-k}x^{k}+\sum_{k=1}^n\begin{bmatrix}n-1\\k\end{bmatrix}(-1)^{n-k}x^k(n-1)\\
&=\sum_{k=1}^n\Bigg(\begin{bmatrix}n-1\\k-1\end{bmatrix}+(n-1)\begin{bmatrix}n-1\\k\end{bmatrix}\Bigg)(-1)^{n-k}x^k\\
&=\sum_{k=0}^n\begin{bmatrix}n\\k\end{bmatrix}(-1)^{n-k}x^k
\end{aligned}
$$
### 普通幂转上升幂
$$
x^n = \sum_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}(-1)^{n-k}x^{\overline{k}}
$$
依然使用归纳法证明,这里略了。
### 上升幂转普通幂
$$
x^{\overline{n}} = \sum_{k=0}^n\begin{bmatrix}n\\k\end{bmatrix}x^k
$$
还是归纳法,还是略。
### 总结四个变换
$$
x^n = \sum_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}x^{\underline{k}}
$$
$$
x^{\underline{n}}=\sum_{k=0}^n\begin{bmatrix}n\\k\end{bmatrix}(-1)^{n-k}x^k
$$
$$
x^n = \sum_{k=0}^n\begin{Bmatrix}n\\k\end{Bmatrix}(-1)^{n-k}x^{\overline{k}}
$$
$$
x^{\overline{n}} = \sum_{k=0}^n\begin{bmatrix}n\\k\end{bmatrix}x^k
$$
咋记呢,首先我们发现 $x^{\overline{k}} \ge x^k \ge x^{\underline{k}}$,所以再由下降幂转普通幂,普通幂转上升幂的过程中,一定会有一个 $(-1)^{n-k}$。
第一类斯特林数是从下降幂和上升幂转到普通幂用;第二类斯特林数是从普通幂转到下降米和上升幂用。
两种幂互相转化用到的斯特林数不同,然后记住第一个变化即可。
# Prüfer 序列
小众乐子知识点。
## 引入
Prüfer 序列可以将一个带标号 $n$ 个节点的无根树用 $[1,n]$ 中的 $n-2$ 个整数表示。
其实就是完全图的生成树与数列之间的双射,因为这个性质,所以 Prüfer 数列常用在组合计数问题上。
## 对树建立 Prüfer 序列
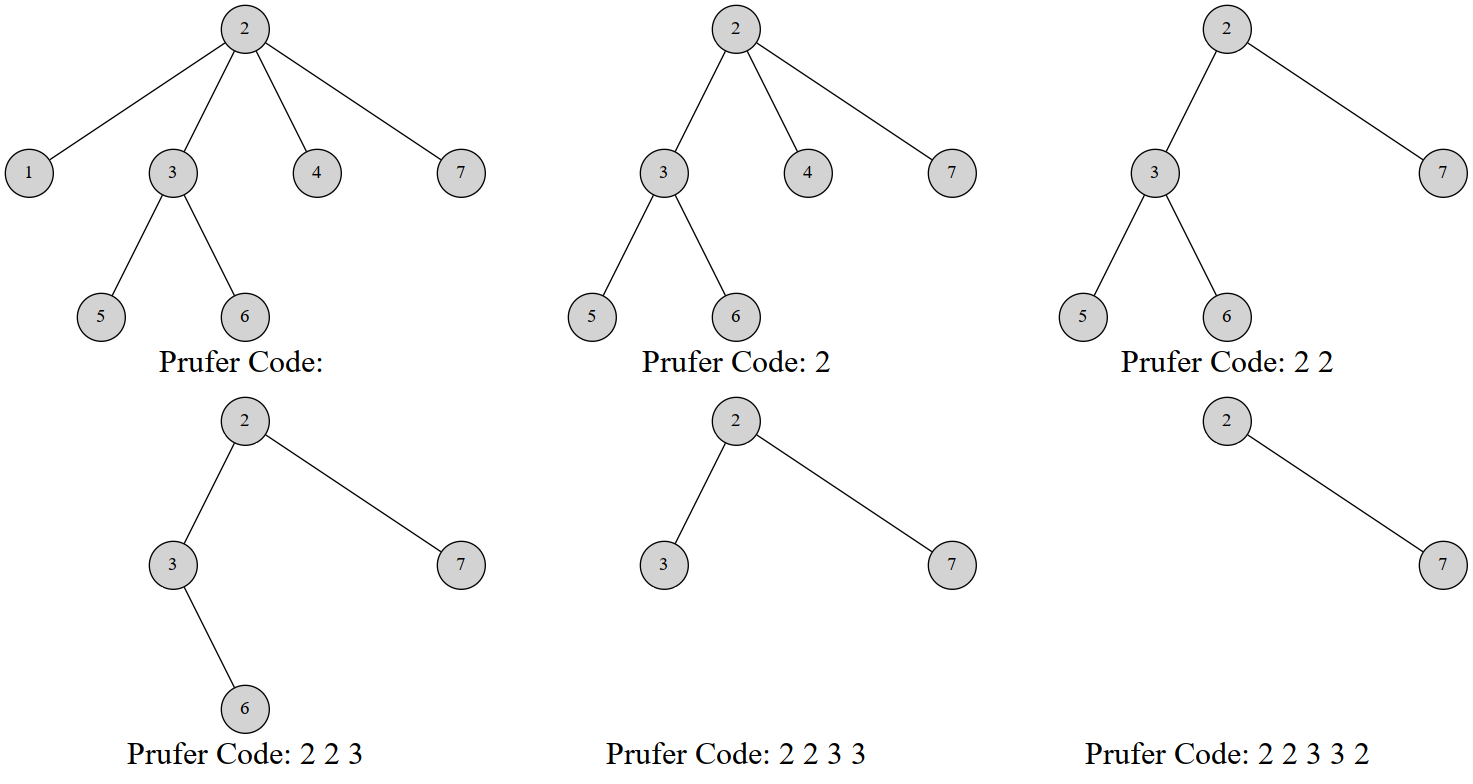
Prüfer 序列是这样建立的:每次选择一个编号最小的叶节点并删掉它,然后在序列中记录它连接到的那个节点,重复 $n-2$ 次后就只剩下两个节点,就结束了。
给张图(来自 OI Wiki)
用优先队列维护堆显然可以做到 $O(n\log n)$。
但也有线性的构造方式。
可以线性构造的原因是叶节点的性质,叶子节点的个数是单调不升的。每次删掉一个叶子节点,要么又新增一个,要么不增。
### 过程
维护一个指针 $p$。初始时指针 $p$ 指向编号最小的叶节点。同时我们维护每个节点的度数,方便我们知道在删除叶节点的过程中是否产生了新的叶节点。流程如下:
1. 删除 $p$ 指向的节点,维护度数,检查是否产生新的叶节点。
2. 如果产生新的叶节点,假设编号为 $x$,我们比较 $p,x$ 的大小关系。如果 $x > p$,那么不做操作;否则立即删除 $x$,然后检查删除 $x$ 后是否产生新的叶节点,重复步骤 $2$,直到未产生新的叶节点或者新节点的编号 $>p$。
3. 让指针自增直到遇到一个未被删除叶节点为止。
可以证明,每条边最多被访问一次(在删度数的时候),而指针最多遍历每个节点一次,因此复杂度是 $O(n)$ 的。
代码来自洛谷模板,在这个题中为了好写是一棵有根树,$f$ 数组表示的是每个节点的父节点,$p$ 数组表示的就是 Prüfer 序列。
```cpp
for(re int i=1;i<=n-1;i++) f[i] = read() , du[f[i]]++;
for(re int i=1,j=1;i<=n-2;i++,j++)
{
while(du[j]) j++;//找叶子节点
p[i] = f[j];
}//所以这个复杂度是 O(n) 的
for(re int i=1;i<=n-2;i++) ans ^= 1ll * i * p[i];
cout << ans;
```
### 小性质
1. 在构造完 Prüfer 序列后原树中会剩下两个节点,其中一个一定是编号最大的点 $n$。
2. 每个节点在序列中出现的次数是其度数减 $1$。
## 根据 Prüfer 序列重建树
重建树的方法也是类似的,通过 Prüfer 序列我们可以得到原树上每个点的度数。然后你也可以得到编号最小的叶节点,而这个叶节点一定与 Prüfer 序列的第一个数连接,然后我们同时删掉这两个点的度数,这就是大致思路。
同理,我们用优先队列维护度数为 $1$ 的节点的小根堆,同样能做到 $O(n\log n)$。
也是同理,这个也有线性做法。
同理,让 $p$ 指向编号最小的叶子节点,$i$ 指针指向 Prüfer 序列的第 $i$ 位。
1. 删除 $p$ 指向的节点的度数,将它与 Prüfer 序列的第 $i$ 位相连,同时删除 $i$ 的度数,检查是否产生新的叶节点。
2. 如果产生新的叶节点,假设编号为 $x$,我们比较 $p,x$ 的大小关系。如果 $x > p$,那么不做操作;否则立即删除 $x$ 的度数,连边,然后检查删除 $x$ 度数后是否产生新的叶节点,重复步骤 $2$,直到未产生新的叶节点或者新节点的编号 $>p$。
3. 让指针自增直到遇到一个未被删除叶节点为止。
```cpp
for(re int i=1;i<=n-2;i++) p[i] = read() , du[p[i]]++;
p[n-1] = n;
for(re int i=1,j=1;i<=n-1;i++,j++)
{
while(du[j]) j++;
f[j] = p[i];
while(i <= n-1 && !(--du[p[i]]) && p[i] < j) f[p[i]] = p[i+1] , i++;
}
for(re int i=1;i<=n;i++) ans ^= 1ll * i * f[i];
cout << ans;
```
## Cayley 公式(Cayley's formula)
对于一棵完全图 $K_n$ 有 $n^{n-2}$ 棵生成树。
这个用 Prüfer 序列证明最简单。任意一个长度为 $n-2$ 的值域为 $[1,n]$ 的整数序列都可以通过 Prüfer 序列双射对应一个生成树,于是方案数就是 $n^{n-2}$。
## 图联通方案数
> 一个 $n$ 个点 $m$ 条边的带标号无向图有 $k$ 个连通块,我们希望添加 $k-1$ 条边使得整个图连通。求方案数。
设 $s_i$ 表示每个连通块的数量,然后最后的答案就是
$$
n^{k-2}\cdot \prod_{i=1}^ks_i
$$
说实话,OI-Wiki 上的证明没咋看懂,如果想了解可以去[OI-Wiki](https://oi-wiki.org/graph/prufer/#%E5%9B%BE%E8%BF%9E%E9%80%9A%E6%96%B9%E6%A1%88%E6%95%B0)上看一下证明。
## 给定度数无根树计数
> 给定每个点的度数,求出有多少符合条件的无根树。
设每个点的度数是 $d_i$ ,先给出结论:个数 $=
\frac{(n-2)!}{\displaystyle \prod_{i=1}^n(d_i-1)!}
从 Prüfer 序列的角度来看,由 Prüfer 序列的性质 2 ,我们可以知道度数为 d_i 的点会在 Prüfer 序列中出现 d_i-1 次,那么这其实就是可重集排列数了,总共 n-2 个位置,每个 d_i 会重复 d_i-1 次,套上可重集排列数的公式,就是答案。
还需要注意一些特判,比如 n=1 或者 \sum d_i \not= 2n-2 的情况,后者是铁定无解的,前者要看 d_1 ,如果是 0 ,答案就是 1 ,其余都是 0 。