各种信奥结论

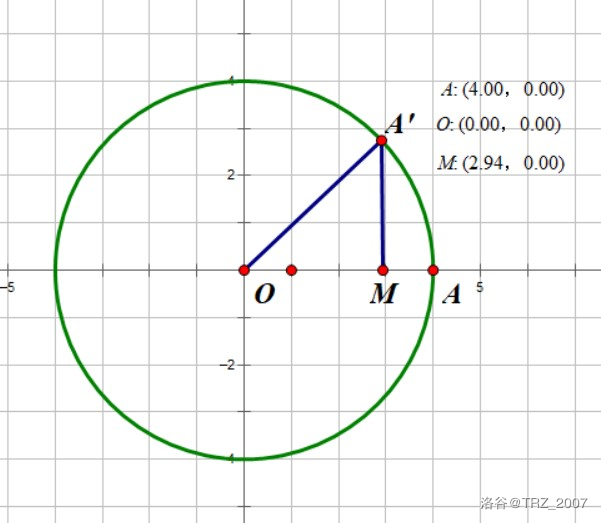
## 1：在45度的坐标系点变换中，$(x,y)$会变换成$(\frac{x+y}{\sqrt{2}},\frac{x-y}{\sqrt{2}})$和$(\frac{y-x}{\sqrt{2}},\frac{x+y}{\sqrt{2}})$。 证明： 设A的坐标为$(x,y)$。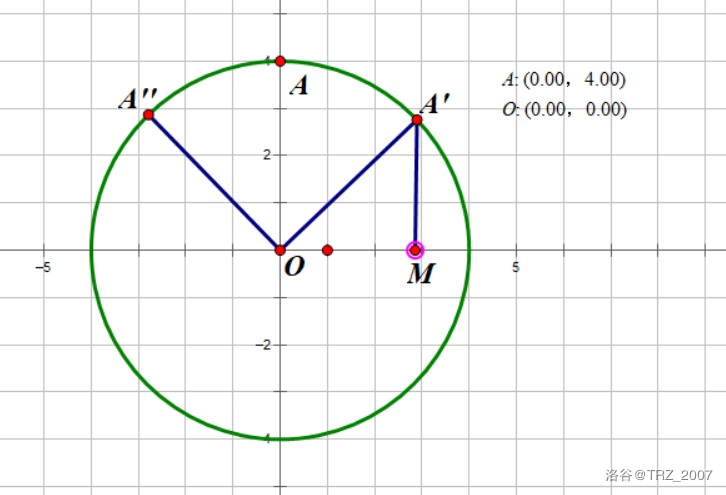 1.当A在$x$轴上时：  作M使得$A'M \perp AO$ $\because OA=OA',\angle AOA'=45^\circ$ $\therefore \triangle A'MO$ 是等腰直角三角形 $\therefore OM=A'M=\frac{A'O}{\sqrt{2}}=\frac{x}{\sqrt{2}}$ $\therefore A'(\frac{x}{\sqrt{2}},\frac{x}{\sqrt{2}})$ 由于对称性，点A向第四象限移动45度的坐标 $A''(-\frac{x}{\sqrt{2}},-\frac{x}{\sqrt{2}})$ 2.当A在$y$轴上时  作M使得$A'M \perp x$轴 $\because OA=OA',\angle AOA'=45^\circ$ $\therefore \angle A'OM=\angle AOM-\angle AOA'=45^\circ$ $\therefore \triangle A'MO$ 是等腰直角三角形 $\therefore OM=A'M=\frac{A'O}{\sqrt{2}}=\frac{y}{\sqrt{2}}$ $\therefore A'(\frac{y}{\sqrt{2}},\frac{y}{\sqrt{2}})$ 由于对称性，点A向第二象限移动45度的坐标 $A''(-\frac{y}{\sqrt{2}},\frac{y}{\sqrt{2}})$ 3.当A在象限中时： 以第一象限为例，其他都相同。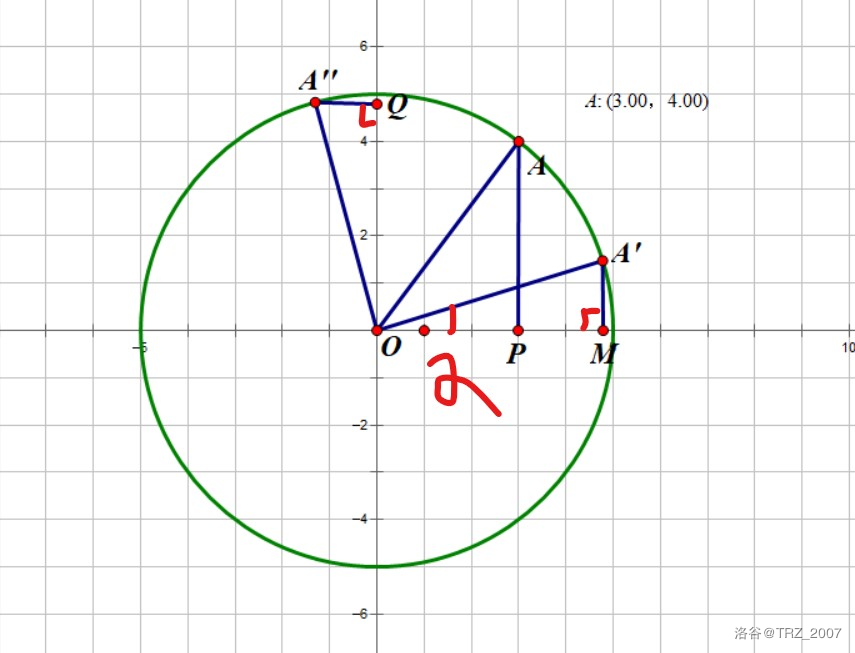  作$Q,M$使得$A'M\perp x$轴，$A''Q\perp y$轴，易证$\triangle A''QO\cong\triangle AMO$ 设$A'(x1,y1)$，圆O半径为$r$ 则：$y1=r.\sin \alpha,x1=r.\cos\alpha,\sin(\alpha+45^\circ)=\frac{y}{r},\cos(\alpha+45^\circ)=\frac{x}{r}$ 我们考虑拆$\sin(\alpha+45^\circ)=\frac{y}{r}$和$\cos(\alpha+45^\circ)=\frac{x}{r}$，得： $\therefore \begin{cases}\sin\alpha.\cos45^\circ + \cos\alpha.\sin45^\circ=\frac{y}{r}\\\cos\alpha.\cos45^\circ-\sin\alpha.\sin45^\circ=\frac{x}{r}\end{cases}$ 解得：$\begin{cases}\sin\alpha=\frac{x+y}{\sqrt{2}.r}\\\cos\alpha=\frac{y-x}{\sqrt{2}.r}\end{cases}$ $\therefore x1=r.\cos\alpha=\frac{y-x}{\sqrt{2}},y1=r.\sin\alpha=\frac{x+y}{\sqrt{2}}$ $\therefore A'(\frac{y-x}{\sqrt{2}},\frac{x+y}{\sqrt{2}})$ $\because \triangle A''QO\cong\triangle AMO$ $\therefore A'M=A''Q,OQ=OM$ $\therefore A''(\frac{x+y}{\sqrt{2}},\frac{x-y}{\sqrt{2}})$ 综上，命题成立。