2023.1 做题记录
RyexAwl
·
·
个人记录
2023.1.2
CF1772G Gaining Rating
题目链接
简要题意
给你 n 个人,每个人有一个能力值 a_i 你的能力值最开始从 x 开始,目标是到 y。如果你打赢了一个能力值小于等于你的人,那么你的能力值 +1,反之 -1。问你在尽可能平均的情况下,也就是如果你要打 i 那么不应该存在一个 j 使得打 i 的场次比打 j 的场次多。求最少场次,或者判断无解。
#### 题解
难点在实现。思路直接看官方题解。
```cpp
i64 calc(i64 p,i64 q) {
if (p % q == 0) return p / q;
return p / q + 1;
}
void solve() {
scanf("%d%lld%lld",&n,&x,&y);
rep(i,1,n) scanf("%lld",&a[i]);
std::sort(a + 1, a + 1 + n);
int st = 0; i64 px = x;
rep(i,1,n) {
if (px >= a[i]) {
++ st; ++ px;
}
}
if (st >= y - x) {
printf("%lld\n",y - x);
return;
}
if (st <= n - st) {
puts("-1");
return;
}
i64 ans = 0;
rep(i,st,n) {
if (i != n && a[i + 1] <= x + i) continue;
i64 m = 0;
if (i != n) m = calc(1ll * a[i + 1] - x - i,2 * i - n);
if (x + i >= y) {
ans += y - x;
printf("%lld\n",ans);
return;
}
i64 r = calc(y - x - i,2 * i - n);
if (i == n || r + 1 <= m) {
ans += r * n;
x += r * (2 * i - n);
ans += y - x;
printf("%lld\n",ans);
return;
} else {
x += m * (2 * i - n);
ans += m * n;
}
}
}
```
### CF1765H Hospital Queue
[题目链接](https://www.luogu.com.cn/problem/CF1765H)
#### 简要题意
有 $ n $ 个病人来排队看病,一种合法的排队方案需要满足以下条件:
一、${\forall}$ $ 1 $ ${\leq}$ $ i $ ${\leq}$ $ n $,编号为 $ i $ 的病人必须排在前 $ p_i $ 位。
二、${\forall}$ $ 1 $ ${\leq}$ $ i $ ${\leq}$ $ m $,编号为 $ a_i $ 的病人必须排在编号为 $ b_i $ 的病人前面。
你需要对于每一位病人,求出在所有合法的排队方案中,他能排在的最靠前的位置。
$1\le n\le 2000,0\le m\le 2000$。
#### 题解
##### 算法 I
对于每个病人 $i$,在 $[1,p_i]$ 内二分答案,每次相当于单点修改 $p_i$ 判是否合法,拓扑排序贪心每次取能到的权值最小的点即可。
复杂度 $O(n(n+m)\log ^2n)$。
T 飞了。
##### 题解 II
对于每个点限制在一个前缀内,可以倒着做转化为每个点限制在一个后缀内。这样的好处是我们可以看成在某个时刻将某个点“加入 / 点亮”,即加入比删容易。
这样可以做到 $O(n(n+m))$。
> 总结:
>
> - 时光倒流。如果每个点贡献一个前缀,可以时光倒流成贡献后缀。对于类似加入比删容易(包括复杂度更低)的问题可以很方便的处理。
### CF1637F Towers
[题目链接](https://www.luogu.com.cn/problem/CF1637F)
#### 简要题意
给定一棵包含 $n$ 个点的树,第 $i$ 个点的高度为 $h_i$。你可以在这 $n$ 个点中建任意多个塔,对于每个塔,你都可以指定其所在的点的编号及其势能。建一个势能为 $e$ 的塔需要花费 $e$ 枚硬币(需要保证 $e>0$)。
对于一个树上的点 $x$,我们称其接收到了信号,当且仅当在树上存在两个建了塔的点 $u,v$(需要保证 $u\neq v$,但不需要保证 $x\neq u$ 或 $x\neq v$),使得 $x$ 在从 $u$ 到 $v$ 的路径上,且 $\min(e_u,e_v)\geqslant h_x$。
请求出最少需要花费多少枚硬币,才能使得树上所有点都能接受到信号。
- $2\leqslant n\leqslant 2\times 10^5$。
- $1\leqslant h_i\leqslant 10^9$。
#### 题解 I
注意到至少有一个点取最大值,钦定取最大值的为根,枚举根,那么转化为对于任意点 $x$,以 $x$ 为根的子树内存在至少一个点 $v$ 满足 $e_v\ge h_x$。
考虑进行子树合并,令 $f[u]$ 表示考虑以 $u$ 为根的子树的最小花费,如何合并答案。
一种直接的想法是 $f[u]\gets \sum_{v\in son(u)}f[v]$,令 $val$ 表示以 $u$ 为根的子树除了 $u$ 外的点 $h$ 的最大值。若 $val<h_u$,令 $f[u]\gets h_u-val$。
证明也很简单,对于任意一种合法的方案数,我们将 $v$ 子树㕯 $e$ 取 $h_u$ 的减少,我们总是能得到一种对称的,不超过 $v$ 子树内最大值的方案。
换根维护这个 dp 即可。
复杂度 $O(n)$。
> 总结:
>
> - 对于 $u$ 在 $x,y$ 路径上的限制,考虑钦定一个点为根,转化到子树内的限制。
>
> - 子树合并 dp 的贪心。及其分析方式,将从子树增量出来的结果减回去。
#### 题解 II
注意到只会在叶子上有权值。
钦定 $h$ 最大的为根,对于根必须两棵不同的子树内存在 $e\ge h_{rt}$。
对于其他点只要子树内有一个即可。
这样就不用换根了。
复杂度 $O(n)$。
> 总结:
>
> - 对于 $u$ 在 $x,y$ 路径上的限制,考虑钦定一个点为根,转化到子树内的限制。并且选的足够好可以避免换根。
## 2023.1.3
### 一个经典的双指针问题
#### 简要题意
给定 $n$ 个整数构成的序列 $a$,以及整数 $k$,求最多可以选出多少对不交的点对 $(i,j)$ 满足 $a_i+a_j\ge k$。
$n\le 10^6$。
#### 题解
```cpp
std::sort(a + 1,a + 1 + n);
std::reverse(a + 1,a + 1 + n);
int ans = 0;
for (int i = 1,j = n; i <= n; i++) {
while (j > i && a[i] + a[j] < k) j--;
if (j <= i) break;
++ ans; j--;
}
```
相关题目:
- [CF1690E Price Maximization](https://www.luogu.com.cn/problem/CF1690E)
- [CF1729D Friends and the Restaurant](https://www.luogu.com.cn/problem/CF1729D)
### CF1674D A-B-C Sort
[题目链接](https://www.luogu.com.cn/problem/CF1674D)
#### 简要题意
你有三个数组 $a,b,c$,$a$ 初始有 $n$ 个元素,$b$ 和 $c$ 初始是空的。
你可以执行以下算法:
第一步,当 $a$ 不为空,重复从 $a$ 取出末尾的元素并将其插入 $b$ 的正中间。如果 $b$ 当前有奇数个元素,可以选择将 $a$ 中取出的元素插入 $b$ 正中间元素紧挨着的左侧或右侧的空位上。
在此之后 $a$ 变成空的,$b$ 有 $n$ 个元素。
第二步,当 $b$ 不为空,重复取出 $b$ 正中间的元素并将其插入 $c$ 的末尾。如果 $b$ 当前有偶数个元素,可以选择从正中间两个元素中取出一个。
在此之后 $b$ 变成空的,$c$ 有 $n$ 个元素。
具体流程可以参照样例解释。求你是否可以通过以上算法让 $c$ 以非降序排序。 如果能,输出一行 `YES`,否则输出 `NO`。
$1\le n\le 2\times 10^5,1\le a_i\le 10^6$。
#### 题解
注意到,我们可以把 $b\to c$ 转化为 $c\to b$,这样我们相当于判能不能把 $a$ 和 $c$ 操作成相同的。
这里的关键点是对操作的过程进行刻画,我们从后向前两两分组,$a_n,a_{n-1}$ 必定是各占 $b_1,b_{n}$,其他的类似。
那么我们从末尾开始两两分组,判 $a$ 和 $c$ 的多重集是否相同即可。
```cpp
const int N = 2e5 + 5;
int n,a[N],c[N];
void solve() {
scanf("%d",&n);
rep(i,1,n) scanf("%d",&a[i]);
rep(i,1,n) c[i] = a[i];
std::sort(c + 1,c + 1 + n);
for (int i = n; i >= 1; i -= 2) {
if (i != 1) {
if (a[i - 1] > a[i])
std::swap(a[i],a[i - 1]);
if (a[i] != c[i] || a[i - 1] != c[i - 1]) {
puts("NO"); return;
}
} else {
if (a[i] != c[i]) {
puts("NO"); return;
}
}
}
puts("YES");
}
```
> 总结:
>
> - 操作可逆找不变量。
>
> - 对于每次取出放中位数的问题考虑相邻操作两两分组观察。因为每插完两个后就可以很好的刻画子结构。
### CF1650D Twist the Permutation
[题目链接](https://www.luogu.com.cn/problem/CF1650D)
#### 简要题意
你有一个 $1\sim n$ 的排列 $a$,最开始时 $a_i=i$,你可以对这个排列 $a$ 执行 $n$ 次操作,每次指定一个正整数 $x$ ,第 $i$ 次时将 $a_1\sim a_i$ 中的每个数 $a_j$ 变成 $a_{j+x\bmod i}$。
现在告诉你 $n$ 次操作完成后的排列 $a$,请你还原出每轮选择的 $x$ 的值。
$n\le2\times 10^3$。
#### 题解
注意到,这个操作后面的可能会影响前面的,不好。
考虑时光倒流将 $a$ 操作成 $[1,2,3,...,n]$ 这样后面的操作不会对前面操作好的结果影响。
复杂度 $O(n^2)$。
这里循环移位的写法。
$$
[1,2,3,4,5]\to [2,3,4,5,1]
$$
```cpp
void modify(int i,int j) {
rep(k,1,n) q[k] = p[k];
rep(k,1,i) q[k] = p[((k - 1) + j) % i + 1];
rep(k,1,n) p[k] = q[k];
rep(k,1,n) pos[p[k]] = k;
}
```
$$
[1,2,3,4,5]\to [5,1,2,3,4]
$$
```cpp
void modify(int i,int j) {
rep(k,1,n) q[k] = p[k];
rep(k,1,i) q[k] = p[((k - 1) - j + i) % i + 1];
rep(k,1,n) p[k] = q[k];
rep(k,1,n) pos[p[k]] = k;
}
```
即把下标转成 0-based 然后再偏移回来。
> 总结:
>
> - 后面的影响前面操作的结果,不好。考虑时光倒流,后面的不影响前面操作的结果,好。
>
> - 循环移位的实现技巧与用模运算刻画环。
## 2023.1.4
### P1117 [NOI2016] 优秀的拆分
[题目链接](https://www.luogu.com.cn/problem/P1117)
#### 简要题意
$T$ 组数据,每次数据给定一个长度为 $n$ 的小写字母构成的字符串,令 $val(S)$ 表示将 $S$ 划分成形如 $\mathrm{AABB}$ 的方案数。求:
$$
\sum_{1\le l\le r\le n}val(S[l,r])
$$
$1\le T\le 10$,$n\le 30000$。
#### 题解
问题可以转化成 $S$ 中选形如 $\mathrm{AABB}$ 的子串的方案数。
类似 meet in the middle 的思路,枚举端点,分别计算前缀中有多少个后缀形如 $\mathrm{AA}$ 和后缀中有多少个前缀形如 $\mathrm{BB}$。
具体的,令 $f_i$ 表示有多少个从 $i$ 开始的形如 $\mathrm{AA}$ 的子段,$g_i$ 表示有多少个以 $i$ 结尾的形如 $\mathrm{AA}$ 的子段。
那么答案即:
$$
\sum_{i=1}^{n-1}f_{i+1}\times g_i
$$
那么问题转化为了如何计算 $f$ 和 $g$。
对于 $S=\mathrm{AA}$,其周期结构满足 $\forall 1\le i\le |A|,S_i=S_{i+|A|}$。那么如果确定了 $|A|$,每个间距 $|A|$ 的字符是对应的。
枚举 $|A|=len$,每 $len$ 个位置放一个关键点,即 $len,2len,3len,...,$ 的位置上各放一个关键点。(即类似模运算的周期刻画)
那么对于任意一个 $\mathrm{AA}$ 的子串,如果其起始位置为 $i$,那么第一段为 $[i,i+len)$,区间内一定恰好有一个关键点,第二段为 $[i+len,i+2len)$,区间内一定恰好有一个关键点,并且这两个关键点一定是相邻的。
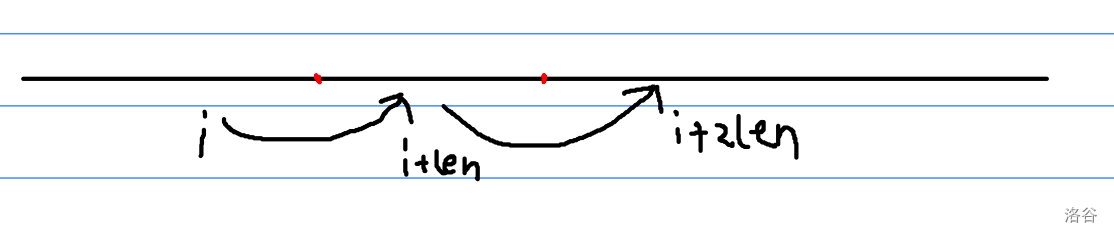
那么考虑枚举相邻的关键点,这样的总复杂度是 $O(n\log n)$ 的。
考虑子串 $S[l,r]$,$r-l+1=2\times len$,$l\in ((i-1)\times len,i\times len],r\in [(i+1)\times len,\min(n,(i+2)\times len))$。
若其可以划分成 $\mathrm{AA}$ 一定有 $\mathrm{lcp}(\mathrm{suf}(i\times len),\mathrm{suf}((i+1)\times len))+\mathrm{lcs}(\mathrm{pre}(i\times len),\mathrm{pre}((i+1)\times len))-1\ge len$。并且该条件是充要的。
那么我们可以先求一下 $\mathrm{lcp}$ 和 $\mathrm{lcs}$,然后转化为 $S[l,r]$ 可以划分成 $\mathrm{AA}$ 当且仅当 $[l,r]\subseteq [x,y]$。那么贡献的左端点和右端点一定是一段区间,差分即可。
复杂度 $O(Tn\log n)$。
注意 SA 多测清空的实现细节。
```cpp
struct SA {
int n;
char str[N];
int sa[N],rk[N << 1],oldrk[N << 1],id[N],cnt[N],height[N];
int minv[20][N],lg[N];
int calc(int l,int r) {
int len = lg[r - l + 1];
return std::min(minv[len][l],minv[len][r - (1 << len) + 1]);
}
int lcp(int i,int j) {
if (i == j) return n - i + 1;
return calc(std::min(rk[i],rk[j]) + 1,std::max(rk[i],rk[j]));
}
int lcs(int i,int j) {
return lcp(n - i + 1,n - j + 1);
}
// 多测 sa 清空 cnt 和 rk。因为 rk[i + w] 可能会用到比 n 大的,所以,,,
void build() {
memset(cnt,0,sizeof cnt);
memset(rk,0,sizeof rk);
int m = std::max(300,n);
rep(i,1,n) ++ cnt[rk[i] = str[i]];
rep(i,1,m) cnt[i] += cnt[i - 1];
per(i,n,1) sa[cnt[rk[i]] --] = i;
for (int w = 1; w < n; w <<= 1) {
int tot = 0;
rep(i,n-w+1,n) id[++ tot] = i;
rep(i,1,n) if (sa[i] > w) id[++ tot] = sa[i] - w;
rep(i,0,m) cnt[i] = 0;
rep(i,1,n) ++ cnt[rk[i]];
rep(i,1,m) cnt[i] += cnt[i - 1];
per(i,n,1) sa[cnt[rk[id[i]]] --] = id[i];
memcpy(oldrk,rk,sizeof rk);
for (int i = 1,j = 1; i <= n; i++) {
if (i == 1 || ((oldrk[sa[i]] == oldrk[sa[i - 1]]) && (oldrk[sa[i] + w] == oldrk[sa[i - 1] + w])))
rk[sa[i]] = j;
else
rk[sa[i]] = ++ j;
}
if (rk[sa[n]] == n) break;
m = rk[sa[n]];
}
rep(i,1,n) rk[sa[i]] = i;
rep(i,1,n) {
if (rk[i] == 1) {
height[rk[i]] = 0; // 初始化成 0,不过应该不影响,因为默认就是 0,不会动。
continue;
}
int j = sa[rk[i] - 1],k = std::max(0,height[rk[i - 1]] - 1);
while ((j + k <= n) && (i + k <= n) && (str[i + k] == str[j + k])) ++ k;
height[rk[i]] = k;
}
lg[1] = 0; lg[2] = 1;
rep(i,3,n) lg[i] = lg[i / 2] + 1;
rep(i,1,n) minv[0][i] = height[i];
rep(i,1,19) for (int j = 1; j + (1 << i) - 1 <= n; j++)
minv[i][j] = std::min(minv[i - 1][j],minv[i - 1][j + (1 << (i - 1))]);
}
} LCP,LCS;
```
> 总结:
>
> - 类似 meet in the middle 的枚举技巧。
>
> - 对于循环子串问题可以考虑枚举 $|A|$,撒关键点,考虑相邻两个关键点,这样复杂度是 $O(n\log n)$ 的。这样 $S_i$ 和 $S_{i+|A|}$ 有对称性。
>
> - SA 多测清空 cnt 和 rk。
>
### POJ 3693 Maximum repetition substring
[题目链接](http://poj.org/problem?id=3693)
#### 简要题意
给定一个长度为 $n$ 的字符串 $S$,求重复次数最多的连续重复子串。
输出字典序最小的重复次数最多的连续重复子串。
$n\le 10^5$。
#### 题解
题目要考虑的是所有整周期的子串,不妨把条件松一下,考虑所有非整周期子串,对于具有长为 $L$ 的循环节,长度为 $m$ 的循环子串,对答案的贡献为 $\lfloor \frac{M}{L} \rfloor$。
而对于长度为 $m$ 的字符串具有长度为 $k$ 的循环节的充要条件是具有长度为 $m-k$ 的 border。
对于这种子串周期相关的问题,同样考虑枚举循环节长度 $len$,撒关键点,枚举相邻关键点,只要循环次数 $\ge 2$ 一定会跨过至少一对相邻的关键点。
考虑计算每对相邻关键点的贡献。如果关键点分别位于位置 $i<j$。
那么子串 $[l,r]$,$[i,j]\subseteq [l,r]$,其具有长为 $len$ 的循环节的充要条件是:
- $[l,j]$ 具有长为 $len$ 的循环节。
- $[i,r]$ 具有长为 $len$ 的循环节。
而 $[l,j]$ 具有长为 $len$ 的循环节等价于 $\mathrm{pre}(i),\mathrm{pre}(j)$ 具有长为 $i-l$ 的公共后缀(将循环节转化为 border),$[i,r]$ 具有长为 $k$ 的循环节等价于 $\mathrm{suf}(i),\mathrm{suf}(j)$ 具有长为 $i-j$ 的公共前缀。
那么跨过 $[i,j]$ 的最长的 $[l,r]$ 即可通过求两个后缀的 $\mathrm{lcp}$ 和两个前缀的 $\mathrm{lcs}$ 解决。
接下来考虑如何输出字典序最小的答案,合法的左端点可以看成一段连续的区间,取这段区间 rk 最小的即可。
> 总结:
>
> - 对于字符串周期,可以把整周期松成 $S_i=S_{i+m}$ 的不强制整周期。
>
> - 长度为 $m$ 的字符串具有长度为 $k$ 的循环节的充要条件是具有长度为 $m-k$ 的 border。
>
> - 对于子串周期相关的问题,同样考虑枚举循环节长度 $len$,撒关键点,枚举相邻关键点,只要循环次数 $\ge 2$ 一定会跨过至少一对相邻的关键点。
>
> - 对于最小化字典序问题可以转化为求 rk 最小的左端点。
### CF319D Have You Ever Heard About the Word?
[题目链接](https://www.luogu.com.cn/problem/CF319D)
#### 简要题意
给定一个长度为 $n$ 的字符串 $S$,每次找到一个最短的且最靠左的形如 $XX$ 的子串,将其缩成 $X$,求最后无法操作的字符串。
$n\le 5\times 10^4$。
#### 题解
一个重要的性质是如果当前删的子串 $XX$ 满足 $|X|=len$,那么将其缩了后一定不会新产生子串 $YY$ 满足 $|Y|\le len$。
那么我们缩的子串的长度一定是单调不减的,考虑按 $len$ 从小到大缩子串。如果缩了至少一个子串就重构信息。
找 $|X|=len$ 形如 $XX$ 的子串可以用 [P1117 [NOI2016] 优秀的拆分](https://www.luogu.com.cn/problem/P1117) 中的方法,这样总复杂度是 $O(n\log n)$,而找到所有删除的位置是均摊 $O(n)$ 的。因为每次重构一定至少删除了一个长度为 $len$ 的子串,这里存在一个自然根号,$1+2+...+\sqrt{n}=O(n)$ 所以重构次数是 $O(\sqrt{n})$ 的。
因为后缀数组重构复杂度比较大,所以这里采用字符串哈希 + 二分维护后缀的 lcp 和前缀的 lcs,总复杂度 $O(n\sqrt{n}+n\log ^2n)$。
> 总结:
>
> - intuitition。如果不考虑新增的子串,那么删除的子串长度具有单调性可以按删除长度从小到大处理,而考虑新增的子串只用证明新增的子串中一定不存在 $YY$,$|Y|\le len$ 即可。
>
> - 找所有形如 $XX$ 的子串的技巧。
>
> - 从长为 $n$ 的序列从小到大依次删 $1,2,3,...$ 的子段,重构信息,这里有自然根号,重构次数 $O(\sqrt{n})$。
>
> - 字符串哈希 + 二分维护后缀的 lcp 和前缀的 lcs。
### CF1607D Blue-Red Permutation
[题目链接](https://www.luogu.com.cn/problem/CF1607D)
#### 简要题意
有 $n$ 个数,每个数是红色或蓝色。你可以进行无限次操作(也可以 $0$ 次),每次操作你可以:
1. 把一个蓝色的数 $-1$ 。
2. 把一个红色的数 $+1$ 。
问是否能将这 $n$ 个数变成 $1$ 到 $n$ 的排列,是就输出 `YES` ,否则 `NO` 。
$1\le n\le 2\times 10^5,-10^9\le a_i\le 10^9$。
#### 题解
将其看成权值和下标的匹配,每个蓝色的下标可以匹配的权值是一段前缀,每个红色的下标可以匹配的权值是一段后缀。
考虑一个简单的问题,如果只有一种颜色,怎么做。那是很好做的,排序,依次匹配即可。(当然也可以利用类似括号匹配的刻画方式从而支持数据结构维护,这里先不讨论)
考虑能不能将其转化为单种颜色的问题。由于每个蓝色的下标可以匹配的权值是一段前缀,每个红色的下标可以匹配的权值是一段后缀。猜一下蓝色匹配的一定是一段前缀,红色一定匹一段后缀。
可以使用调整法证明,若存在 $x<y$,$x$ 红 $y$ 蓝一定可以调整成 $x$ 蓝 $y$ 红。
这样就转化为两个独立的单色问题了。
复杂度 $O(n\log n)$。
> 总结:
>
> - 每个位置匹配一段前缀 / 一段后缀的解法:1. 贪心,代码实现简单; 2. 刻画成括号匹配,数据结构维护。
>
> - intuitition。蓝色匹前缀,红色匹后缀。利好调整法。
### CF1618D Array and Operations
[题目链接](https://www.luogu.com.cn/problem/CF1618D)
#### 简要题意
给定 $n$ 个数和一个数 $k$,要求对这 $n$ 个数进行 $k$ 次操作,每次操作取出两个数 $a_i,a_j (i\neq j)$,并将 $\lfloor \frac{a_i}{a_j} \rfloor$ 加进得分中,其中 $\lfloor \frac{x}{y} \rfloor$ 为不超过 $\frac{x}{y}$ 的最大整数。
$k$ 次操作后,将剩下的 $n-2k$ 个数直接加入到得分中。
求最终得分的最小值。
$1\le t\le 500,1\le n\le 100,0\le k\le \lfloor \frac{n}{2} \rfloor$。
#### 题解
可以通过调整法证明一定是对前 $2k$ 大的数两两配对。
两个不同的数配对贡献 $0$,相同的数配对贡献 $1$,我们要最大化不同的数配对的数量,这是一个经典的模型,很容易处理。
> 总结:
>
> - 通过调整法证明一定是对前 $2k$ 大的数两两配对。
>
> - 经典模型,最大化不同数配对的数量。
## 2023.1.5
### CF1731F Function Sum
[题目链接](https://codeforces.com/contest/1731/problem/F)
#### 简要题意
给定 $n,m$,对于长度为 $n$ 的序列 $a$,令 $\mathrm{lsl}(i)$ 表示多少个 $j$ 满足 $1\le j<i$ 且 $a_j<a_i$,$\mathrm{grr}(i)$ 表示多少个 $j$ 满足 $i<j\le n$ 且 $a_j>a_i$,定义 $f(a)=\sum_{i=1}^na_i\times [\mathrm{lsl}(i)<\mathrm{grr}(i)]$。
求所有长度为 $n$,满足 $\forall 1\le i\le n,1\le a_i\le m$ 的 $f(a)$ 的和。
$1\le n\le 50,2\le m\le 998244353$。
#### 题解
枚举贡献的位置 $i$,$\mathrm{lsl}(i)$,$\mathrm{grr}(i)$,权值 $x$:
$$
\sum_{i=1}^n\sum_{j=0}^{i-1}\sum_{k=j+1}^{n-i}\binom{i-1}{j}\binom{n-i}{k}\sum_{x=1}^m(x-1)^j(m-x)^k(m-x+1)^{i-1-j}x^{n-i-k}x
$$
经典的多项式前缀和模型。
其中 $(x-1)^j(m-x)^k(m-x+1)^{i-1-j}x^{n-i-k}x$ 是关于 $x$ 的 $n$ 次多项式。
那么:
$$
f(m)=\sum_{x=1}^m(x-1)^j(m-x)^k(m-x+1)^{i-1-j}x^{n-i-k}
$$
是关于 $m$ 的 $n+1$ 次多项式。
拉插即可,复杂度 $O(n^4)$。
> 总结:
>
> - 多项式前缀和,拉插。
### CF1535F String Distance
[题目链接](https://www.luogu.com.cn/problem/CF1535F)
#### 简要题意
对于字符串 $a,b$,你可以进行下列操作:
- 选择其中任意一个字符串的子串,并将其从小到大排序。
我们定义 $f(a,b)$ 为字符串 $a,b$ 进行上述操作使 $a=b$ 所需的最小次数,特别的,如果无论如何都不可能使 $a=b$,$f(a,b)=1337$。例如:
- $f(\texttt{"ab"},\texttt{"ab"})=0$,因为这两个字符串本身就已经相同。
- $f(\texttt{"ba"},\texttt{"ab"})=1$,你可以将整个第一个字符串排序。
- $f(\texttt{"ebcda"},\texttt{"ecbda"})=1$,你可以选择第二个字符串的第二个到第四个字符排序。
- $f(\texttt{"a"},\texttt{"b"})=1337$,显然无法通过上述操作使这两个字符串相同。
给定 $n$ 个长度相等的字符串 $s_1,s_2,\cdots,s_n$。
求 $\sum\limits_{i=1}^n\sum\limits_{j=i+1}^nf(s_i,s_j)$。
$1\leq n\leq2\times10^5;|s_1|=|s_2|=\cdots=|s_n|;\sum|s_i|\leq2\times10^5;
题解
注意到每次操作不改变一个字符串构成字符的多重集,考虑按多重集划分等价类,对于两个不同等价类的字符串对其贡献一定是 1337。
接下来考虑如何计算同一个等价类内所有串对的贡献。注意到如果两个串属于同一个等价类,那么其贡献为 0,1,2。
贡献为 0 当且仅当相等。
重点是数贡献为 1 的字符串对的个数。
贡献为 1 当且仅当两个串不相等且存在一个子段 [l,r] 满足其在一个串中是有序的。并且两个串 [1,l-1],[r+1,m] 均是相等的。
这里直觉上是对该对串求个 lcp 和 lcs,如果不相等一定有 lcp + lcs < m。并且删掉 lcp 和 lcs 后剩下的中间的部分一定有一个串是有序的,因为再往外扩因为其钦定为不动点,所以也没意义。
这里的突破口是注意到有序的串的字典序一定比操作的串字典序小,考虑把等价类内所有串按字典序排序,在字典序小的串上统计。
考虑在字典序小的串上枚举排好序的子段,计算有多少个字典序比该串大的串中有多少个能匹配上。
直接枚举子段是单个串 O(m^2) 的,但是注意到我们可以对每个左端点双指针枚举最长的单调的右端点,这样每个串是 O(m) 的,然后钦定 lcp,这样一个字符串对只会被统计一次。lcp 的限制可以发现符合要求的一定是一段区间(因为已经按字典序排好序了),单调栈刻画,后面相等的限制用 trie 维护反串即可。
复杂度 O(nm\log n)。
总结:
-
按字典序排序。两个串的 lcp。
-
钦定前缀 / 后缀,trie 维护串 / 反串。
-
单调栈刻画前缀的后缀 \min 结构。
-
双指针维护极长单调子段。
2023.1.6
CF1385C Make It Good
题目链接
简要题意
-
给定你一个长为 n 的序列 A ,请问要在这个序列中擦除长度为多少的前缀,才能使这个序列是一个好的序列。
-
对好的序列的定义:假定有一个序列 B,你可以每次从序列的首项或末项取出一个数字放在序列 C 的末尾。假如存在一种方案使得 C 不降,那么 B 就是好的序列。
-
本题有 T 组数据。1\leq T\leq 2\times 10^4
题解
这里一个重要的视角转化是序列 B 是好的充要条件是其是单峰的。然后找极长单峰后缀即可。
总结:
- 每次取首项或末项放在末尾有序的充要条件是其是单峰序列。
2023.1.6
P6793 [SNOI2020] 字符串
题目链接
简要题意
有两个长度为 n 的由小写字母组成的字符串 a,b,取出他们所有长为 k 的子串(各有 n-k+1 个),这些子串分别组成集合 A,B。现在要修改 A 中的串,使得 A 和 B 完全相同。可以任意次选择修改 A 中一个串的一段后缀,花费为这段后缀的长度。总花费为每次修改花费之和,求总花费的最小值。
#### 题解
考虑将 $A$ 中的字符串和 $B$ 中的字符串一一匹配,这样对于一对字符串其花费即为 $k$ 减两个字符串的 LCP。
对于 LCP 考虑使用后缀数组刻画,构造字符串 $s=a+\#+b$。
那么对于 $a$ 从 $i$ 开始的长度为 $k$ 的子串与 $b$ 从 $j$ 开始的长度为 $k$ 的子串的 LCP 长度即 $\min(k,\mathrm{LCP}(suf(i),suf(n+1+j)))$。其中 $suf(i)$ 表示字符串 $s$ 从 $i$ 开始的后缀。
总后缀数组中拿出所有关键点(即 $a,b$ 中从前 $n-k+1$ 个位置开始的后缀),串成新的链。
问题转化成了给一个 $2m$ 个点的链,$i,i+1$ 之间由带非负边权的边,每个点有点权 $0$ 或 $1$,保证恰好 $m$ 个 $0$ 和 $m$ 个 $1$。
将一个 $0$ 和一个 $1$ 匹配起来的费用是两个点路径中最小边的边权,求权值和最大的将 $0$ 和 $1$ 匹配起来的完美匹配。
对于路径上的最小边,考虑建 kruskal 重构树刻画,注意到我们可以自底向上贪心匹配,能在下面匹就在下面匹。
复杂度 $O(n\log n)$。
> 总结:
>
> - 刻画成两两匹配。
>
> - 费用是路径边权 $\min$,考虑使用 kruskal 重构树刻画。可以泛化成一棵树,每个点 $0$ 或 $1$,一组匹配价值是路径边权 $\min$,$0$ 和 $1$ 两两匹配,求最大的完美匹配。(当然甚至可以是无向图)
>
> - 后缀数组结构可以看成特殊的链(树),结合笛卡尔树 / kruskal 重构树可以有更强的结构。如果包含信息过多可以只保留关键点将中间的边缩掉。
### P6624 [省选联考 2020 A 卷] 作业题
[题目链接](https://www.luogu.com.cn/problem/P6624)
#### 简要题意
小 W 刚刚在离散数学课学习了生成树的知识:一个无向图 $G=(V,E)$ 的生成树 $T$ 为边集 $E$ 的一个大小为 $|V|-1$ 的子集,且保证 $T$ 的生成子图在 $G$ 中连通。
小 W 在做今天的作业时被这样一道题目难住了:
给定一个 $n$ 个顶点 $m$ 条边(点和边都从 $1$ 开始编号)的无向图 $G$,保证图中无重边和无自环。每一条边有一个正整数边权 $w_i$,对于一棵 $G$ 的生成树 $T$,定义 $T$ 的价值为:$T$ 所包含的边的边权的最大公约数乘以边权之和,即:
val(T)=\left(\sum\limits{i=1}^{n-1} w{ei}\right) \times \gcd(w{e1},w{e2},\dots,w{e_{n-1}})
其中 $e_1,e_2,\dots,e_{n-1}$ 为 $T$ 包含的边的编号。
小 W 需要求出 $G$ 的所有生成树 $T$ 的价值之和,他做了很久也没做出来,请你帮帮他。由于答案可能很大,你只需要给出答案对 $998244353$ 取模后的结果。
$1\leq n\leq 30, 1\leq m \leq \frac {n(n-1)}{2}, 1\leq w_i \leq 152501$。
#### 题解
考虑枚举 $\gcd$,计算边权 $\gcd=d$ 的所有生成树的边权和。转化为求 $d\mid \gcd$ 的所有生成树的边权和,相当于保留一些边计算所有生成树的边权和。
这里计算次数可以只算保留边数 $\ge n-1$ 的,总次数是 $O(\frac{\sum d(w_i)}{n-1})$。这里大概是 $144\times n$。
那么问题转化为计算生成树所有边的边权和。首先有暴力的 $O(mn^3)$ 做法。
更高效的做法是把边的边权改成多项式 $w_ix+1$,在模 $x^2$ 的运算意义下求行列式。最后一次项的系数即答案。
这里考虑一下求逆。
$$
(ax+c)(bx+d)\equiv 1\pmod{x^2}
$$
$$
(ax+c)(bx+d)=abx^2+adx+cbx+cd
$$
这里构造 $cd=1$,$ad=-cb$。
可以得到:
$$
d=\frac{1}{c},b=-\frac{a}{c^2}
$$
这里消元每次找非 $0$ 行相当于找常数项非 $0$ 行,这样才可逆。
总复杂度 $O(n^3\frac{\sum d(w_i)}{n-1})
总结:
-
枚举 \gcd,计算边权 \gcd=d 的所有生成树的边权和。转化为求 d\mid \gcd 的所有生成树的边权和。
-
剪枝。只保留出现次数 \ge n-1 的约数,那这样的约数至多 O(\frac{\sum d(w_i)}{n-1}) 种。
-
计算所有生成树的边权和的 O(n^3) 做法。以及利用多项式化加为乘的技巧。\sum w_i=[x^1]\prod(w_ix+1)。
2023.1.7
P5303 [GXOI/GZOI2019]逼死强迫症
题目链接
简要题意
ITX351 要铺一条 2 \times N 的路,为此他购买了 N 块 2 \times 1 的方砖。可是其中一块砖在运送的过程中从中间裂开了,变成了两块 1 \times 1 的砖块!
ITX351 由此产生了一个邪恶的想法:他想要在这条路上故意把两块 1 \times 1 的砖块分开铺,不让两块砖有相邻的边,其他砖块可以随意铺,直到整条路铺满。这样一定可以逼死自身强迫症 sea5!
也许下面的剧情你已经猜到了——他为此兴奋不已,以至于无法敲键盘。于是,他请你帮忙计算一下,有多少种方案可以让自己的阴谋得逞。
N \le 2 \times 10^9$,$T \le 500
题解
看起来很矩阵快速幂。对于每块砖,如果是横着放的定义其在靠左的列放置,如果是竖着放的定义其在所在列放置。
并且注意到实际上我们只用考虑两个 1\times 1 的不在同一列,因为我们总是能拿掉两条 2\times 1 的递归成 n-1 列的不限制横向的方案:
对于一种方案考虑从左到右扫描线观察,每块砖在其放置的列枚举,可以观察到以下性质:
-
扫完前 i 列放置的所有砖,一定完全覆盖了 1\sim i 列中的位置。
-
第 i 列放置砖的方案只与第 i-1 列有关。
那么可以直接搞一个 dp,f[i,S,0/1/2] 表示扫完前 i 列放置的所有砖,对第 i+1 列影响状态是 S 且当前放了 0/1/2 个 1\times 1 的砖的方案数。
矩阵快速幂优化即可。
总结:
CF1772F Copy of a Copy of a Copy
题目链接
简要题意
给定一张 n 行 m 列的黑白图片(下标从 1 开始),每一个单元格都被涂上了黑色或白色(1 或者 0)。
我们对这张图片进行了若干次(可能为零次)操作,每一次操作都是下列两种之一:
- 选择一个单元格,这个单元格不能在图片的边缘(即,单元格所在行不能是 1 或 n 行,所在列不能是 1 或 m 列),并且这个单元格被四个不同颜色的单元格包围(中间 0 四周 1,反之亦然),将这个单元格涂成相反的颜色;
- 复制一份当前图片。
两种操作不一定会交替进行。
给出你初始图片与 k 份复制图片,一共 k+1 份图片,这 k+1 份图片是被随机打乱的。
你的任务是恢复操作的顺序。若有多种可能答案,只输出其中一个即可。
所有数据保证答案一定存在。
#### 题解
考察两个相邻版本之间的操作,注意到不同格子是互不影响的。即一个格子变色后其相邻的格子一定不会再变色了。那么所有颜色发生变化的格子一定是互不相邻的。
那么只要我们确定了版本顺序就很好确定修改操作。
这里一开始的想法是在可以相邻的之间连边然后找链,但是这个问题看起来很难,不行。
这里的突破口是网格中可修改的格子个数是随着时间顺序递减的,那么我们对所有版本求可修改的格子个数即可唯一确定版本顺序。
复杂度 $O(nmk+k\log k)$。
> 总结:
>
> - 修改格子的独立性。
>
> - 利用时间顺序可修改格子个数的递减性唯一确定顺序。
## 2023.1.8
### CF1514D Cut and Stick
[题目链接](https://www.luogu.com.cn/problem/CF1514D)
#### 简要题意
给定一个长度为 $n$ 的序列 $(n\le3\times10^5)$,可以对其进行三种操作:
1. 把一段区间片段中所有的数从原来的区间里剪下来
2. 把这些数按照在原来序列里的排列顺序重新拼接成序列
3. 最后形成一个或者多个片段的序列,使最开始的序列中每一个数都属于某一个片段。
要求:给定 $q$ 个询问 $(q\le3\times10^5)$ ,每次给出一个区间的左右端点,将这个区间分成若干个片段,使得每个片段内任意元素出现的次数不严格大于 $\lceil\frac{x}{2}\rceil$ ($x$ 为该片段长度)。求可以分成的最少片段数目。
#### 题解
如果区间中的众数出现 $m$ 次,区间长度为 $len$。
若 $m\le len-m+1$,那么答案是 $1$。
否则感性理解是 $len-m$ 个其他元素和 $len-m+1$ 个众数分一组,剩下的众数一个一组。
可以证明其是最优的。
首先可以证明最优解一定满足每组众数都是区间中的众数,因为一定存在至少一组众数是区间中的众数,我们可以将不是众数的组合并到该组,并且不会变劣。
接下来可以证明在满足每组众数都是区间中的众数的前提下我们总是能将众数外的元素合并到一组,其他组只有一个众数。
那么现在转化为求区间众数。
1. 莫队算法,维护区间中的 cnt 和 cntcnt,使用值域分块维护 cntcnt 的和,可以做到 $O(1)$ 修改 $O(\sqrt{n})$ 查询。总复杂度 $O(m\sqrt{n})$。
2. 因为我们只查询绝对众数,所以可以线段树维护区间摩尔投票法的结果,使用 vector + 二分判定。复杂度 $O((n+m)\log n)$。
> 总结:
>
> - 全局众数与子集众数的 intutition。
>
> - 分组合并调整法。
>
> - 莫队算法 + 值域分块维护区间众数。
>
> - 摩尔投票 + 数据结构判定维护区间绝对众数。
### CF1493C K-beautiful Strings
[题目链接](https://www.luogu.com.cn/problem/CF1493C)
#### 简要题意
$T$ 组数据,每组数据开头给出 $n$ 和 $k$ ,接下来一个长度为 $n$ 的字符串,
您需要构造一个长度为 $n$ 的字符串使得每种在字符串里出现过的字符出现次数恰好为 $k$ 的倍数,且字典序大于等于输入字符串。若有多解输出字典序最小解,否则输出`-1`。
注:字符均为小写字母。
$1\le k\le n\le 10^5$。
#### 题解
必要条件为 $k\mid n$,并且其是充分的,因为我们总是能构造 `zzz....`。
考虑如何最小化字典序,考虑枚举 lcp,注意到一定是 lcp 越长越小,然后考虑固定 lcp 如何构造,考虑枚举不同的第一位进行钦定,判定,构造都很好做。
> 总结:
>
> - 字典序相关的问题考虑枚举 lcp 与第一位不同的。类似后缀数组的 height,lcp 越大字典序越小。
### CF1525F Goblins And Gnomes
[题目链接](https://www.luogu.com.cn/problem/CF1525F)
#### 简要题意
给一张 $n$ 个点 $m$ 条边的 DAG,以及轮数正整数 $k$,在第 $i$ 轮开始前可以进行以下两种操作之一任意次:
- 选中点 $u$,删除 $u$ 的所有出度,耗费 $1$ 的时间。
- 选中点 $u$,删除 $u$ 的所有入度,耗费 $1$ 的时间。
要求在第 $i$ 轮准备后,DAG 的最小路径覆盖 $>i$。
第 $i$ 轮前的操作会影响第 $i$ 轮后的图(即操作不独立)。
同时给定长度为 $k$ 的正整数数组 $x,y$,如果第 $i$ 轮前耗费了 $t$ 的准备时间,那么第 $i$ 轮的收益为 $\max(0,x_i-ty_i)$。
总收益为所有轮的收益和,求最优的策略能够最大总收益,构造方案。
$2\le n\le 50,0\le m\le \frac{n(n-1)}{2},1\le k\le n-1,1\le x_i,y_i\le 10^9$。
#### 题解
DAG 最小路径覆盖可以转化为二分图最大匹配,限制可以转化为第 $i$ 轮准备后二分图最大匹配 $< n-i$,准备操作可以看成二分图中删除一个点及其所有相连的边。
核心模型可以看成:删除最少的点,让二分图最大匹配减 $1$。(同 [CF1721F Matching Reduction](https://www.luogu.com.cn/problem/CF1721F))
这个模型的结构很简单,删一个点至多让最大匹配减 $1$ 并且我们总能找到一个点删掉它后让最大匹配减 $1$,因为二分图最大匹配 = 最小点覆盖,我们每次删掉一个最小点覆盖中的点总能让最小点覆盖减 $1$。
那么前 $i$ 轮至少要删的点数我们总是能唯一确定的,令 $f[i,j]$ 表示前 $i$ 轮删了 $j$ 个点的最大收益。
使用匈牙利算法求最小点覆盖的复杂度是 $O(nm)$,dp 的复杂度是 $O(n^3)$。
> 总结:
>
> - 核心模型:删除最少的点,让二分图最大匹配减 $1$。将其转到最小点覆盖上。(应用几个基本的原理,我们可以在 DAG 最小路径覆盖,最小点覆盖,最大独立集,最大匹配之间做转化,对点的操作考虑往点上转)
>
> - 限制转化前 $i$ 轮至少删 $j$ 个点,这样就可以 dp 了。
## 2023.1.9
### P5324 [BJOI2019]删数
[题目链接](https://www.luogu.com.cn/problem/P5324)
#### 简要题意
对于任意一个数列,如果能在有限次进行下列删数操作后将其删为空数列,则称这个数列可以删空。一次删数操作定义如下:
>记当前数列长度为 $k$ ,则删掉数列中所有等于 $k$ 的数。
现有一个长度为 $n$ 的数列 $a$,有 $m$ 次修改操作,第 $i$ 次修改后你要回答:
经过 $i$ 次修改后的数列 $a$,至少还需要修改几个数才可删空?
每次修改操作为单点修改或数列整体加一或数列整体减一。
$1\le n,m\le 150000,1\le a_i\le n,0\le p\le n$,$1\le p\le n$ 时 $1\le x\le n$,表示将 $a_p$ 修改为 $x$,$p=0$ 时 $x\in \{1,-1\}$,表示全体加 $x$。
#### 题解
首先我们需要对可以被删空的序列有更好的刻画(即找到相对简单,方便后续处理的充要条件)。按权值从小到大考虑,注意到对于所有出现过的权值 $i$,必须要满足序列中 $\le i$ 的权值个数恰好为 $i$,这是充要的。
注意这里“修改”的数是很有自由度的,所以考虑将所有被“修改”的数删除,只保留不修改的数,最大化不动点个数。
接下来我们先考虑所有权值都在 $1\sim n$ 之间的情况(即不存在整体加一和整体减一的修改的情况)。
考虑如何判断保留的不动点是否是合法的。同样的从小到大考虑,首先对于任意保留的权值 $i$(即保留的数中权值 $i$ 的个数不为 $0$),保留的 $\le i$ 的数的个数必须 $\le i$,并且我们要保证将 $<i$ 的权值“补齐”了之后 $\le i$ 的个数仍然不超过 $i$。并且满足这两个条件后一定可以构造出一组解,即这是充要的。那么可以归纳为如果从小到大保留的权值依次为 $x_1<x_2<...<x_k$。那么首先 $x_1$ 的出现次数小于等于 $x_1$,$x_2$ 的出现次数小于等于 $x_2-x_1$,$x_3$ 的出现次数小于等于 $x_3-x_2$,...,$x_k$ 的出现次数小于等于 $x_k-x_{k-1}$。
那么有了判断的充要条件后,考虑贪心选保留最多的。
正着贪心不好做,考虑倒着贪心,不难写出如下代码:
```cpp
int calc() {
memset(cnt,0,sizeof cnt);
rep(i,1,n) ++ cnt[a[i]];
int lst = n + 1,res = 0;
per(i,n,1) {
if (!cnt[i]) continue;
if (lst > i) {
lst = std::max(1,i - cnt[i] + 1);
res += i - lst + 1;
continue;
}
if (i - cnt[i] + 1 >= lst) continue;
int pos = std::max(1,i - cnt[i] + 1);
res += lst - pos;
lst = pos;
}
return res;
}
```
考虑如何处理不在 $1\sim n$ 中的权值,对于不在 $1\sim n$ 中的权值一定会被修改,所以我们只考虑在 $1\sim n$ 之间的权值中最多保留多少即可。
```cpp
int calc() {
memset(cnt,0,sizeof cnt);
rep(i,1,n) if (a[i] >= 1 && a[i] <= n) ++ cnt[a[i]];
int lst = n + 1,res = 0;
per(i,n,1) {
if (!cnt[i]) continue;
if (lst > i) {
lst = std::max(1,i - cnt[i] + 1);
res += i - lst + 1;
continue;
}
if (i - cnt[i] + 1 >= lst) continue;
int pos = std::max(1,i - cnt[i] + 1);
res += lst - pos;
lst = pos;
}
return res;
}
```
到这里的期望得分为 $47$。
考虑使用数据结构维护贪心,为了方便数据结构维护我们需要对贪心做一个等价变形:
```cpp
int calc() {
memset(cnt,0,sizeof cnt);
memset(d,0,sizeof d);
rep(i,1,n) if (a[i] >= 1 && a[i] <= n) ++ cnt[a[i]];
rep(i,1,n) {
d[std::max(1,i - cnt[i] + 1)] ++;
d[i + 1] --;
}
rep(i,1,n) d[i] += d[i - 1];
int res = 0;
rep(i,1,n) {
if (!d[i]) ++ res;
}
return res;
}
```
接下来有两种做法维护上述贪心:
1. 首先考虑如果没有整体 $+1/-1$ 如何做,我们可以动态维护数组 $d$ 中 $0$ 的个数,每次修改都是 $O(1)$ 的。整体 $+1/-1$ 可以看成是值域的偏移,那么可以转化为区间询问,但是贡献的位置要特殊维护一下,使用线段树维护区间加操作,区间 $\min$ 和区间 $\min$ 的个数即可。
2. 对每个位置维护对该位置产生贡献的最靠左的位置,每次值域的移动是 $O(1)$ 的,可以很快的计算区间移动的贡献。
> 总结:
>
> - 正难则反,按权值从小到大考虑,即按删除过程从后向前考虑。
>
> - 对于最小化修改个数的题,如果修改自由度很大,转而考察不动点,转化为最大化保留不动点。
>
> - 数据结构优化贪心。
>
> - 如果要维护 $cnt$ 上的信息,将全体加减看成值域偏移。
>
> - 每次值域变化是 $O(1)$ 的,可以很快维护贡献。
### P5319 [BJOI2019]奥术神杖
[题目链接](https://www.luogu.com.cn/problem/P5319)
#### 简要题意
给定一个由 $0\sim 9$ 和 $.$ 构成的长度为 $n$ 的字符串以及 $m$ 个二元组 $(S_i,V_i)$,其中 $S_i$ 是个由 $0\sim 9$ 构成的字符串,$V_i$ 是一个正整数。
求一种把字符串中的每个 $.$ 替换为 $0\sim 9$ 中某个字符的方案使得字符串的价值最大。
字符串的价值:初始价值为 $1$,对于每个二元组 $(S_i,V_i)$,$S_i$ 在字符串中每出现一次就给价值乘上 $V_i$,最后的结果取几何平均值。即形如 $\sqrt[k]{\prod_{i=1}^k V_i}$。
$1\le n\le 1501,1\le m\le 1501,\sum |s_i|\le 1501$。
#### 题解
几何平均值很抽象,我们可以通过取 $\ln$ 将其转化为代数平均值。
$$
\ln(\sqrt[k]{c})=\frac{1}{k}\ln c
$$
那么:
$$
\ln \left( \sqrt[k]{\prod_{i=1}^k V_i} \right)=\frac{1}{k}\sum_{i=1}^k\ln V_i
$$
而最大化代数平均数是经典的 $01$ 分数规划问题,二分答案即可,check 就是很典的 ACAM + dp。
注意这里我们 check 要求 $\sum \ln V_i-x>0$,否则一定存在任何都不出现的,恰好为 $0$,相当于钦定选至少一个。(另一种方式是在 dp 里设一维状态,但是这样常数起飞了)
以及形如 $11111100000$ 的实数域二分取 $l$ 而不是 $r$。
复杂度 $O(|\Sigma| n\sum |s_i|\log V)$,其中 $\Sigma=\{0,1,2,3,4,5,6,7,8,9\}$。
> 总结:
>
> - 取 $\ln$ 化乘为加,几何平均值化为代数平均值。$\ln(\sqrt[k]{c})=\frac{1}{k}\ln c$。
>
> - 最大化代数平均值看成 $01$ 分数规划问题。
>
> - $01$ 分数规划问题 $\max(\sum\frac{a_ix_i}{b_ix_i})$,$x\in \{0,1\}$,且通常有物选择物品个数限制(不能选 $0$ 个,不然不好二分,换句话说分母不能为 $0$)。如果对物品个数没有特殊限制(只有不能选 $0$ 个),那么可以考虑把大于等于号松成大于号,通过精度松一下。
>
> - ACAM + DP。
### P3715 [BJOI2017]魔法咒语
[题目链接](https://www.luogu.com.cn/problem/P3715)
#### 简要题意
给定 $n$ 个字符串 $S_1,S_2,...,S_n$,$m$ 个字符串 $T_1,T_2,...,T_m$。
求从 $S_1,S_2,...,S_n$ 中拼接长度恰好为 $L$ 的所有字符串的方案中,多少种方案满足 $T_1,T_2,...,T_m$ 均不是拼出来的串的子串的方案数。
对于 $60\%$ 的数据:$n,m\le 50,\sum |S_i|\le 100,\sum |T_i|\le 100,L\le 100$。
对于额外 $40\%$ 的数据:$n,m\le 50,\sum |S_i|\le 100,\sum |T_i|\le 100,L\le 10^8,\forall 1\le i\le n,|S_i|\le 2$。
#### 题解
缝合题,注意阅读题目数据范围发现这一事实。
ACAM + DP 即可,对于额外 $40\%$,矩阵加速即可。
### P3991 [BJOI2017]喷式水战改
[题目链接](https://www.luogu.com.cn/problem/P3991)
#### 简要题意
初始燃料序列为空。每次操作会向序列中的 $p_i$ 位置添加 $x_i$ 单位的同种燃料,该燃料每一单位在三种工作状态下能产生的能量分别为 $a_i, b_i, c_i$。
添加的位置 $p_i$ 是指,在添加后,加入的第一个单位燃料前面有 $p_i$ 个单位的原燃料。
全部的 $x_i$ 单位燃料依次放置,然后原来在 $p_i$ 位置的燃料(如果有的话)依次向后排列。
对于一个确定的燃料序列,其能产生的最大总能量为:将序列依次分成"通常-后期-增强-通常"四段(每段可以为空),每一段在对应工作状态下产生的能量之和的最大值。
对于每次添加操作,你需要给出该次操作使得最大总能量增加了多少。
$1\le n\le 10^5,1\le a_i,b_i,c_i\le 10^4,1\le x_i\le 10^9$。
#### 题解
这个操作一看起来有两种思考方向:
1. 维护颜色段
2. 平衡树维护
因为维护连续段一下子想不到合理的答案维护方式,这里考虑分治结构上 pushup。
我们可以直接每个节点上维护个 dp,$f[l,r]$ 表示子树内的段从左到右的阶段在 $[l,r]$ 内的最大能量,这里 pushup 的常数大概是 $35$。
这里分裂比较特殊,因为可能会把一个点拆出两个点。一次操作至多增加两个点,所以点数是不超过 $2n$ 的。
复杂度 $O(n\log n)$。
当然也可以看成 ddp,平衡树维护矩阵连乘积。
> 总结:
>
> - 平衡树维护序列拼接。
>
> - 分治结构上的 dp。
## 2023.1.10
### CF1773D Dominoes
[题目链接](https://www.luogu.com.cn/problem/CF1773D)
#### 简要题意
Dora喜欢玩多米诺骨牌。玩法是在一个 $n×m$ 的表格中标记一些格子,然后用 $2×1$ 的多米诺骨牌填满其他空格子。注意,多米诺骨牌不能放在标记过的格子上。
Dora的弟弟Dani喜欢搞恶作剧,趁Dora不在时,他会在表格中又标记两个格子。请告诉他有多少种标记的方案,使多米诺骨牌无法填充到所有空格子里。
但是Dani只能数到 $10^6$。如果方案数超过 $10^6$,请输出 $10^6$。
保证给定的初始网格可以被 $2\times 1$ 的骨牌密铺。
$1\le n,m\le 1000$。
#### 题解
首先考虑如何判定一个确定好禁用位置的网格是否可以被 $2\times 1$ 的骨牌密铺。把骨牌看成边,格子看成点,连边。当且仅当图中存在完美匹配,该网格图可以被骨牌密铺,按 $(i+j)$ 的奇偶性进行二分图染色,其是二分图。
因此问题可以转化为,给定一张二分图,计算有多少个从中删除两个点的方案使得操作后的二分图不存在完美匹配。
首先方案数超过 $10^6$ 输出 $10^6$ 这一输出方式意味着我们可以考虑缩减二分图规模。如果初始的二分图大小为 $n$。
因为初始有解,所以左部和右部均 $\frac{n}{2}$ 个点,在同一部删两个点后一定不存在完美匹配(两部大小不同)。
因此当 $n>2000$ 时,直接输出 $10^6$。
暴力的想法是枚举两个点判断,但是我们可以只枚举一个点,删掉后最大匹配一定为 $\frac{n}{2}-1$,确定另一个点相当于确定二分图匹配的非必经点,DFS 即可。
复杂度 $O(N^2)$,其中 $N$ 不超过 $2000$。
> 总结:
>
> - 判断网格图是否可以被 $2\times 1$ 的骨牌密铺刻画成二分图完美匹配。
>
> - 答案对某个值取 $\min$ 考虑缩减问题规模。
>
> - 二分图完美匹配可以考察两部的数量关系。利用该性质缩减问题规模。
>
> - 枚举点对的问题可以考虑先枚举一个点再快速确定另一个点,即使两点地位均等但枚举完一个点后另一个点可能会很好确定。
>
> - 二分图最大匹配必经点问题。
>
> - 存在完美匹配的二分图删掉一个点后的最大匹配可以很快的求,变化是常数级别的。同理删掉二分图最大匹配必经点的图的最大匹配也很好求。
## 2023.1.11
### CF1508A Binary Literature
[题目链接](https://www.luogu.com.cn/problem/CF1508A)
#### 简要题意
给你一个正整数 $n$ 和三个长度为 $2\times n$ 的 01 字符串 $s_1,s_2,s_3$。你需要构造一个 01 字符串 $S$,使得:
- 字符串 $S$ 的长度不能超过 $3\times n$。
- $s_1,s_2,s_3$ 当中至少有两个字符串是 $S$ 的子序列。
可以证明一定有解,有多种解时输出任意一种即可。$T$ 组数据。
$1\leq T\leq10^4;1\leq n,\sum n\leq10^5;$。
#### 题解
显然,选两个 LCS 大于等于 $n$ 的就赢了。
但是求 LCS 很困难。这里的突破口是长为 $2n$ 的 $01$ 串至少 $n$ 个 $0/1$。
并且三个 bit,$0,1$ 中选至少有两个相等的(即三个二进制两两异或的 trick)。
那就很容易赢了。
> 总结:
>
> - 突破口:长为 $2n$ 的 $01$ 串至少 $n$ 个 $0/1$。
>
> - 并且三个 bit,$0,1$ 中选至少有两个相等的(即三个二进制两两异或的 trick)。
### CF1656D K-good
[题目链接](https://www.luogu.com.cn/problem/CF1656D)
#### 简要题意
给定一个整数 $n$,请找出一个大于等于 $2$ 的整数 $k$,使得 $n$ 可以表示成 $k$ 个除以 $k$ 的余数互不相同的正整数之和。
数据范围:
- $t$ 组数据,$1\leqslant t\leqslant 10^5$。
- $2\leqslant n\leqslant 10^{18}$。
#### 题解
首先 $n$ 是 $k$-good 的充要条件是:
- $n\ge 1+2+3+...+k$。
- $n\equiv 1+2+3+...+k\pmod{k}$。
即 $n$ 可以写成:
$$
n=k\times q+\frac{k(k+1)}{2},q\ge 0
$$
等价于:
$$
2n=k(2q+k+1)
$$
因为 $k,k+1$ 奇偶性不同,所以一定是一奇一偶,把 $2n$ 质因数分解中 $2$ 和其他约数拆开分解掉即可。
复杂度 $O(t\log n)$。
> 总结:
>
> - $x\ge y,x\equiv y\pmod{m}$ 等价于 $x=m\times q+y,q\ge 0$,不要局限在同余的符号上,注意考察周期结构。
>
> - 凑出类似 $x=k(2q+k+1)$ 的形式,因为 $k,k+1$ 奇偶性不同,所以一定是一奇一偶,把 $x$ 质因数分解中 $2$ 和其他约数拆开分解掉即可。
### CF1427C The Hard Work of Paparazzi
[题目链接](https://www.luogu.com.cn/problem/CF1427C)
#### 简要题意
曼哈顿有 $r$ 条南北向的街道,按从西到东的顺序用数字表示为 $1 , 2 , ... , r$ ,有 $r$ 条东西向的街道,按从南到北的顺序用数字表示为 $1$ , $2$ , $...$ , $r$ 。每条南北向的街道与每条东西向的街道相交,第 $x$ 条南北向道路与第 $y$ 条东西向道路相交的路口用 $(x,y)$ 表示。从路口 $(x,y)$ 移动到路口 $(x',y')$ 需要 $|x-x'|+|y-y'|$ 分钟。
你知道城市有将有 $n$ 位名人出现并且你想尽可能多地给他们拍照。更确切地说,你知道第 $i$ 位名人将恰好在第 $t_i$ 分钟出现在路口 $(x_i,y_i)$ 并只停留相当短的时间,只有当你第 $t_i$ 分钟时在路口才能拍照。你的工作技法娴熟,所以你能瞬间完成拍照。你已经知道了对任意的$i=1,2,\cdots,n-1$ 都有 $t_i<t_{i+1}$ 成立。
输入的第一行是两个正整数 $r$ , $n$ 表示道路的数量和名人的数量,接下来的n行描述名人的出现,第 $i$ 行有三个正整数 $t_i$ , $x_i$ , $y_i$ 表示第 $i$ 位名人将在第 $t_i$ 分钟出现在路口 $(x_i,y_i)$ 。
输出一个整数,为你能拍到的名人的最大数量。
$1\le r\le 500,1\le n\le 10^5$。
#### 题解
显然有一个子序列的 $O(n^2)$ 的 dp。这里的突破口是 $2r$ 步可以走到任意一个点,所以只用判定一个位置前 $2r$ 个位置,复杂度 $O(rn)$。注意 dp 初始化。
> 总结:
>
> - dp 优化的方向,需要处理的转移点很少。利用题目性质剪枝。
>
> - 对于选子序列的 dp 如果确定了子序列开头注意初始化。
### CF1509C The Sports Festival
[题目链接](https://www.luogu.com.cn/problem/CF1509C)
#### 简要题意
给定长度为 $n$ 的序列 $s$,你可以改变序列 $s$ 的顺序,求
$$\sum_{i=1}^n(\max_{j=1}^is_j-\min_{j=1}^is_j)$$
的最小值。
$1\leq n\leq2\times10^3;1\leq s_i\leq10^9;
题解
> 总结:
>
> - $\max_{j=1}^is_j-\min_{j=1}^is_j$ 看成值域的大小。分析值域扩大的过程,转化成取一端的模型。
>
> - 取一端的区间 dp 模型。
### CF1500A Going Home
[题目链接](https://www.luogu.com.cn/problem/CF1500A)
#### 简要题意
给定长度为 $n$ 的序列 $a$,求出任意一组 $x,y,z,w$ 满足:
1. $x,y,z,w$ 互不相同;
2. $a_x+a_y=a_z+a_w$;
如果有解,输出一行 `YES` 后输出任意一组解;否则输出一行 `NO`。
$4\leq n\leq 2\times10^5;1\leq a_i\leq 2.5\times10^6;
题解
首先考虑一些暴力的做法,把 pair 按 a_i+a_j 分类。
对于固定的 a_i+a_j 考虑这样一个模型,无向图,选两条边,点两两不交(CF1566G)。分两类考虑:
-
是菊花图。
-
其他情况。
对于非菊花图,固定一条边,只要边数 \ge 4 一定有解。
对于菊花图如果边数 \ge 4,连出去四个点权值相等,也一定有解(但是解不是钦定的 a_i+a_k)
那么暴力的复杂度可以做到 O(\min(n^2+V))。
总结:
- 无向图,选两条边,点两两不交的模型。在非菊花的情况 \ge 4 条边一定有解,菊花特殊讨论。
CF1486C2 Guessing the Greatest (hard version)
题目链接
简要题意
这是一道交互题。
有一个数字各不相同长度为 n(2\leq n\leq 10^5 的数组 a,在一个查询中,您可以询问子段 a[l...r] 中次大值的位置。您需要在不超过 20 个查询中查找数组中最大元素的位置。
您可以通过输出 "? \;l\; r"(1\leq l \leq r\leq n) 询问,结果是从 l 到r中次大值的位置。数组事先已生成,无法在交互时更改。
您可以通过输出 "!\; p",在那里是数组中最大元素的坐标。
您可以进行不超过 20个查询。输出答案不算作查询。
请注意,样例仅用来表示交互的规则,不保证有逻辑性。
题解
算法 I
递归在 [l,r] 内找,分为 [l,mid],(mid,r] 如果 [l,r] 的次大值在 [l,mid],询问 [l,mid] 的次打值位置,如果与 [l,r] 的次大值位置相同说明最大值在 [l,mid],否则说明在 (mid,r],次大值在 (mid,r] 中同理。询问次数 2\log n,可过 C1。
算法 II
和算法 I 基于同一性质,区间 [l,r] 的次大值位置与全局最大值的位置相同的充要条件是同时包含最大值和次打值。
那么我们只要知道次大值位置和最大值与次大值的位置关系就可以二分了,询问次数 O(\log n)。
总结:
- 对于交互题,两种二分方法,一种是分治,一种是转化为类似 0001111 和 111000 的模型。
2023.1.14
CF1375E Inversion SwapSort
题目链接
简要题意
给定一个长度为 n 的序列 a,求 a 中的所有逆序对 (i_1, j_1), (i_2, j_2), \cdots, (i_m, j_m) 的一个排列 p,使得依次交换 (a_{i_{p_1}}, a_{j_{p_1}}), (a_{i_{p_2}}, a_{j_{p_2}}), \cdots, (a_{i_{p_m}}, a_{j_{p_m}}) 后序列单调不降。
#### 题解
首先考虑简单的情况,即 $a$ 是排列的情况,此时每个权值要挪到的位置是唯一确定的。
这里的 idea 是考虑递归子问题。如果以 $n$ 为右端点的所有逆序对为 $(i_1,n),(i_2,n),...,(i_k,n)$,那么考虑枚举 $(i_1,n),(i_2,n),...,(i_k,n)$ 的一种排列操作,在按排列的顺序操作后的序列为 $b$,满足:
- $b_n=n$。
- $\forall 1\le i<j\le n-1$,如果 $a_i<a_j$,那么 $b_i<b_j$。
- $\forall 1\le i<j\le n-1$,如果 $a_i>a_j$,那么 $b_i>b_j$。
平凡情况为 $a_n=n$,下面考虑非平凡情况。
那么考虑如何构造顺序,根据逆序对的性质所有满足 $a_j>a_n$ 的位置 $j\in \{i_1,i_2,...,i_k\}$。$a_1\sim a_{n-1}$ 的权值可以看成 $[1,a_n),(a_n,n]$。
我们考虑将 $a_1\sim a_{n-1}$ 中 $n$ 拿出来,将 $a_n$ 放回去。即我们将 $a_1\sim a_{n-1}$ 的权值降成 $[1,n-1]$。而这里我们具体的操作是把 $(a_n,n]$ 整体减一映射到 $[a_n,n-1]$。这样我们就能保证 $a_1\sim a_{n-1}$ 中任意两个权值的大小关系是不变的。
这里给出具体的构造操作:
依次操作 $(pos[a_n+1],n)$,$(pos[a_n+2],n)$,$(pos[a_n+3],n),...,(pos[n],n)$。
那么排列的情况总是有解的。
而对于非排列的情况我们可以加第二关键字扰动转化为排列的情况。注意第二关键字一定是按下标从小到大标才是对的。(注意这里转化的等价性)
> 总结:
>
> - 弱化问题,转为排列,构造排列一定有解,加第二关键字扰动成排列。
>
> - 递归子问题,$[1,x),(x,n]$ 将后半部分整体减一,不影响大小关系,合并成 $[1,n-1]$。
### CF125131 & E2 Voting (Hard Version)
[题目链接](https://www.luogu.com.cn/problem/CF1251E2)
#### 简要题意
一共有 $n$ 个选民,你可以付出 $p_{i}$ 的代价让第 $i$ 个选民为你投票,或者,在为你投票的人数达到 $m_{i}$ 时,他会主动为你投票而不用你付出任何代价。
问得到所有选民投票的最小代价。
E1:$n\le 5000$。
E2:$n\le 2\times 10^5$。
#### 题解
注意到,我们可以枚举付出代价的选民的集合,考虑如何判定一种付出代价的选民集合是合法的。
将所有选民按 $m$ 排序,我们称第 $i$ 个选民为按 $m$ 排序后排在第 $i$ 名的选民,其参数用 $m_i,p_i$ 表示。
一种合法的方案一定满足对于任意 $i$,$i$ 前面没付出代价的选民加上所有付出代价的选民数是大于等于 $m_i$ 的。
这里的观察是对于 $i$ 前面的选民,无论其是否付出代价,其总是会对 $i$ 产生贡献。那么对于每个未付出代价的选民 $i$,我们考察 $i$ 后面的选民对 $i$ 产生的贡献,可以将限制转为对于任意 $i$,$i$ 后面付出代价的选民数大于等于 $m_i-(i-1)$。
那么这里我们不难想到一个从后向前的 $O(n^2)$ dp,可过 E1,但是对这个 DP 找不到什么优化的地方,也难用数据结构处理。
这里重要的观察是 $m_i\le m_{i+1}$,令 $b_i=m_i-(i-1)$,一定有 $b_i\le b_{i+1}+1$。
考虑一些 case。对于 $i$,如果其未被付出代价,那么 $[i+1,n]$ 中选付出代价的选民数一定大于等于 $b_i$。而对于 $i-1$:
- 如果 $i-1$ 付出代价,那么 $[i-1,n]$ 中付出代价的选民数大于等于 $b_i+1$,因为 $b_{i-1}\le b_i+1$,所以有 $[i-1,n]$ 中付出代价的选民数一定大于等于 $b_i$。
- 如果 $i-1$ 未付出代价,那么 $[i,n]$ 中付出代价的选民数一定大于等于 $b_i$。
从后向前归纳可得对于任意一种合法的方案,$[i,n]$ 中付出代价的选民个数记为 $f_i$,$\forall j\in [i,n]$ 一定满足 $f_i\ge b_j$,等价于 $f_i\ge \max\limits_{j\in [i,n]}(b_j)$。
令 $c_i=\max\limits_{j\in [i,n]}(b_j)$,我们可以把限制转为 $f_i\ge c_i$,倒着用堆维护即可。复杂度 $O(n\log n)$。
> 总结:
>
> - 通过一些具体推导把限制转为只在意后面选多少个。
>
> - 重要的观察是 $m_i\le m_{i+1}$,令 $b_i=m_i-(i-1)$,一定有 $b_i\le b_{i+1}+1$。
>
> - 限制转化为形如 $f_i\ge c_i$。
### CF1348E Phoenix and Berries
[题目链接](https://www.luogu.com.cn/problem/CF1348E)
#### 简要题意
小 P 在花园里摘红梅和蓝莓。
他一共有 $n$ 棵树,第 $i$ 棵树上有 $a_i$ 个红梅和 $b_i$ 个蓝莓。由于小 P 有强迫症,所以他希望一个篮子里的梅子都来自同一棵树或都是一种颜色的(或两者同时满足)。
给出篮子的最大容量 $m$,求能够被装满的篮子数量的最大值(不必用完所有梅子)。
$1\le n,m\le 500,0\le a_i,b_i\le 10^9$。
#### 题解
每个篮子有两种贡献的方式,考虑先枚举一种贡献方式然后进行最优化,看起来每个梅子来自同一篮子更好枚举,考虑枚举 $(x_i,y_i)$ 满足 $x_i+y_i\bmod m=0$,表示第 $i$ 个篮子选出 $x_i$ 个红梅和 $y_i$ 个蓝莓拼出若干个篮子。
令:
$$
A=\sum a_i,B=\sum b_i
$$
那么固定 $(x_i,y_i)$ 后的最优解即:
$$
\lfloor \frac{A-\sum x_i}{m} \rfloor +\lfloor \frac{B-\sum y_i}{m} \rfloor+\frac{\sum x_i+y_i}{m}
$$
观察到:
$$
A-\sum x_i+B-\sum y_i+\sum x_i+y_i=A+B
$$
我们可以把下取整拆掉:
$$
\lfloor \frac{a}{b} \rfloor=\frac{a-a\bmod b}{b}
$$
最优解可以写成:
$$
\frac{A+B-(A-\sum x_i)\bmod m-(B-\sum y_i)\bmod m}{m}
$$
那么显然是要最小化:
$$
(A-\sum x_i)\bmod m+(B-\sum y_i)\bmod m
$$
这就很简单了。$\sum x_i+\sum y_i\equiv 0\pmod{m}$。
直接令 $f[i,j]$ 表示前 $i$ 组中是否能拼出 $\sum x_i\equiv j\pmod{m}$ 即可。
> 总结:
>
> - 对于多种贡献方法,考虑钦定一些先做,枚举,然后计算贡献。
>
> - $\lfloor \frac{a}{b} \rfloor=\frac{a-a\bmod b}{b}$ 拆下取整。
>
> - $\min(\sum x_i\bmod m)$ 的模型不能直接最优化 dp,应该做可行性 dp。
## 2023.1.15
### CF1368E Ski Accidents
[题目链接](https://www.luogu.com.cn/problem/CF1368E)
#### 简要题意
有一个由 $n$ 个点 $m$ 条边组成的有向无环图,每个点出度至多为 $2$。您需要标记一些点(**不超过** $\frac{4}{7}n$ 个)。标记一个点 $u$ 将会**删除所有与** $u$ **连接的边**。
您需要找到一种标记点的方案,使得删边后的图中每一条路径至多有一条边。
$1\le n\le 2\times 10^5$。
#### 题解
$\frac{4}{7}n$ 的限制有点抽象。这里转化的 trick 是将 $\{1,2,...,n\}$ 划分成三个集合 $A,B,C$ 满足 $|B|\ge \frac{1}{2}|C|,|A|\ge \frac{1}{2}|B|$ 即 $4|A|\ge 2|B|\ge |C|$($7=1+2+4$)
这样 $n=|A|+|B|+|C|\ge |C|\times (1+\frac{1}{2}+\frac{1}{4})$。可以推出 $|C|\le \frac{4}{7}n$。
我们考虑维护只有从 $A\to B$ 的边,删除 $C$ 中的点。
对于 DAG 可以考虑拓扑排序迭代每个点,迭代到点 $x$ 时,如果没有从 $A$ 指向 $x$ 的边就将 $x$ 划分到 $A$ 中,否则划分到 $B$ 中,同时将 $x$ 的所有出点从图中删除。
这样 $B$ 中每个点对应 $A$ 中至少一个出度,$C$ 中每个点对应 $B$ 中至少一个出度。
有:
$$
|B|\le 2|A|,|C|\le 2|B|
$$
这样,对于任意一个 DAG 都是有解的。
> 总结:
>
> - 选子集 $T\subset S$,$|T|\le \frac{a}{b}|S|$ 的问题的一种构造思路,即拼凑比例,划分集合。
>
> - 对于 DAG 可以考虑拓扑排序迭代每个点构造。
### CF1373F Network Coverage
[题目链接](https://www.luogu.com.cn/problem/CF1373F)
#### 简要题意
给你 $n$ 个城市,这 $n$ 个城市首尾相接形成一个环,已知每个城市有一定数量的家庭需要网络。同时每一座城市中有一个网络基站,每一个网络基站可以为一定数量的家庭提供网络,并且第$i$个网络基站只能给第 $i$ 个城市和第 $i+1$ 个城市的家庭提供网络(第 $n$ 个网络基站可以给第 $n$ 座城市和第 $1$ 座城市提供网络)。
现在给你每一座城市需要网络的家庭数量 $a_i$ 和每一个网络基站可以提供的最多网络数量 $b_i$,请你判断能否使得所有的家庭都获得网络,可以则输出 “YES“,否则输出 ”NO“。
$2\le n\le 10^6,1\le a_i,b_i\le 10^9$。
#### 题解
首先考虑一些简单的情况,钦定一条边取 $0$,即链的情况。
一种想法是从端点开始贪,但是这样并不好扩展到复杂情况。
考虑 Hall 定理,合法充要条件是任意选点,所有与点集相邻的边集的边权和不小于所选的点权和,而我们总是能将其拆分成若干个连续段,合法的充要条件是对每个连续段是合法,所以我们可以只考虑连续段。
并且可以扩展到环上,然后就可以 $O(n)$ 做了。
> 总结:
>
> - Hall 定理。
>
> - Hall 定理的应用技巧,很多子集不用考虑。
>
> - 一些复杂的贪心判定过程并不好扩展的复杂情况,需要考虑一些简单的判定条件。
### CF1408E Avoid Rainbow Cycles
[题目链接](https://www.luogu.com.cn/problem/CF1408E)
#### 简要题意
有 $m$ 个集合 $A_1,A_2,\dots,A_m$,它们包含的元素为 $[1,n]$ 中的整数。
在第 $i$ 个集合中删掉元素 $j$ 的代价为 $a_i+b_j$ 。你可以删掉任何集合中的任何元素(也可以不删除)。
现在有一个 $n$ 个节点的无向图,如果删除操作结束以后元素 $x,y(x<y)$ 在集合 $i$ 中同时存在,则在 $x,y$ 间连一条颜色为 $i$ 的边(可以有颜色不同的重边)。
问最小的代价,使得删除完元素后形成的图不存在一个每条边颜色都不同的简单环(环长可以为 $2$)。
$1\le m,n\le 10^5,1\le a_i,b_i\le 10^9$。
#### 题解
考虑建立一张新图然后在新图上搞些事情。
这里建图的 idea 是对题目中判定的图的优化,对于每个集合向属于该集合的所有点连一条边,如果 $j\in A_i$,集合 $i$ 与权值 $j$ 之间的边权为 $a_i+b_j$。
这样原来图中任意一个每天边颜色都不同的简单环一定对应新图中的简单环,并且可以证明新图中的所有简单环一定对应原图中的彩虹环。
这样我们在新图上求一个最大生成树即可。
> 总结:
>
> - 图论 trick:建新图,转化为新图上的图论问题。
>
> - 对于不存在环的限制考虑转化成生成树。
>
### CF1209E Rotate Columns (hard version)
[题目链接](https://www.luogu.com.cn/problem/CF1209E2)
#### 简要题意
给定一个 $n \times m$ 的矩阵,你可以对每一列进行若干次循环移位
求操作完成后每一行的最大值之和的最大值。
$t$ 组测试数据。
$1\le t\le 40,1\le n\le 12,1\le m\le 3000$。
#### 题解
首先有一种显然的 $O(tm3^n)$ 的 dp。转移看起来比较难优化。考虑在状态上优化该 dp,注意到我们可以只保留最大值前 $n$ 大的列,其他列一定不会被用到。
复杂度 $O(tn2^n)$。
> 总结:
>
> - 状态数上优化 dp。只保留少量列。
## 2023.1.18
### P8290 [省选联考 2022] 填树
[题目链接](https://www.luogu.com.cn/problem/P8290)
#### 简要题意
有一棵 $n$ 个节点的无根树,刚开始树上每个节点的权值均为 $0$。KK 想对这棵树进行一些修改,他会任选一个节点作为初始的当前节点,然后重复以下动作:
1. 将当前节点 $i$ 的权值修改为一个**正整数** $x$,需满足 $l_i \leq x \leq r_i$。其中 $l_i, r_i$ 是输入中给出的两个正整数。
2. 结束修改过程,或移动到一个与当前节点相邻的权值为 $0$ 的节点(如果不存在这样的节点,则必须结束修改过程)。
现在 KK 有两个问题:
1. 在修改结束后,可以得到多少棵不同的树,满足树上**非零权值**的最大值和最小值的差小于等于 $K$?其中 $K$ 是输入中给出的一个正整数。
2. 这些满足条件的树的权值之和为多少?(树的权值定义为这棵树上所有节点的权值之和)
你需要输出这两个问题的答案模 $10^9 + 7$。我们认为两棵树不同当且仅当至少存在一个节点的权值不同。
温馨提示:
1. KK 至少会修改一个节点(初始节点)。
2. 实质上 KK 会修改树上的任意一条路径,最后需要满足这条路径上的点的权值最大值和最小值之差小于等于 $K$。
$1\le n\le 200,1\le l_i\le r_i\le 10^9,1\le K\le 10^9$。
#### 题解
先考虑第一问,首先考虑一个简化的问题,多少长为 $n$ 的数组满足 $x\in [l_i,r_i]$ 且 $\max(x_i)-\min(x_i)\le K$。如果我们可以用 $O(B)$ 的复杂度解决该子问题,那么我们不难 $O(n^2)$ 枚举路径对每条路径 $O(B)$ 解决子问题做到 $O(n^2B)$ 的复杂度,并且可以考虑通过一些枚举上的优化(比如用 DP 枚举路径)去做到类似 $O(nB)$ 的复杂度。
一个自然的想法是枚举 $z=\min(x_i)$,这样所有权值就被固定在了 $[z,z+k]$ 内,方案数就是每个变量能取的数的个数乘起来,而每个变量能取的数的个数是关于 $z$ 的分段的一次函数,乘起来就是 $n$ 次多项式,前缀和一下是 $n+1$ 次多项式,分了 $O(n)$ 段,每段选 $n+2$ 个求点值然后插值即可。复杂度 $O(n^3)$。
考虑优化枚举路径的复杂度,我们最后相当于要对所有路径求和,把所有路径的多项式求和后依然是个 $n+1$ 次的多项式。
那么考虑对所有路径求和后的每段多项式求出 $n+2$ 个点值,这里 dp 的复杂度是 $O(n)$ 单个点值,求 $O(n^2)$ 个点值的复杂度是 $O(n^3)$。插值可以用复合转化成插 $1,2,...$插值这里的复杂度是 $O(n^2)$,可以节省常数。
第二问也类似方式搞一下就行了。
> 总结:
>
> - 对于考虑所有路径的问题可以考虑固定一条路径的子问题怎么做然后在枚举路径上做点文章。
>
> - 分段函数。
>
> - 对于每段多项式,暴力求几个点值插值。
>
## 2023.1.19
### P8349 [SDOI/SXOI2022] 整数序列
[题目链接](https://www.luogu.com.cn/problem/P8349)
#### 简要题意
小 D 三岁就学会了出题。
小 D 有一个正整数序列 $a_1, a_2, \dots a_n$ 和一个整数序列 $b_1, b_2, \dots ,b_n$。
小 D 有 $q$ 次查询,每次给出 $x, y$,构造一个新的序列 $c_1,c_2,\dots ,c_n$,其中 $c_i=\begin{cases}1 & a_i=x \\-1 & a_i = y \\ 0 & \text{else}\end{cases}$。
保证 $c_i$ 中至少存在一个 $1$ 与一个 $-1$。他想让你帮他找到一个区间 $[l,r]$,满足 $\sum\limits_{i = l}^r c_i = 0$,并使得 $\sum\limits_{i = l}^r b_i \times [c_i \neq 0]$ 最大,并且区间里的 $c_i$ 不能都为 $0$。你需要输出这个最大值。
注:当条件 $[P]$ 为真时,$[P]=1$,否则 $[P]=0$。
$1\le n\le 3\times 10^5,1\le q\le 10^6,1\le a_i\le n,-10^9<b_i\le 10^9,1\le x,y\le n,x\ne y$,保证每次查询至少含有一个 $1$ 和 $-1$。
#### 题解
首先有一个 $O(cnt_x+cnt_y)$ 的做法。考虑按 $cnt$ 的出现次数根号分治,将所有前缀按 $cnt\le B$ 和 $cnt>B$ 的分两类,将 $cnt\le B$ 的权值定义为小块,$cnt>B$ 的权值定义为大块。
对于小块对小块,复杂度为 $O(B)$。
大块对大块暴力预处理每对,复杂度为 $O(\frac{n^2}{B})$。
接下来考虑小块对大块怎么做。考虑画折线图,大块的权值是 $1$,小块的权值是 $-1$。
注意到,我们可以只保留可能的左端点和右端点。
考虑每个右端点,该右端点会产生贡献当且仅当向左延伸一条线能画到点。
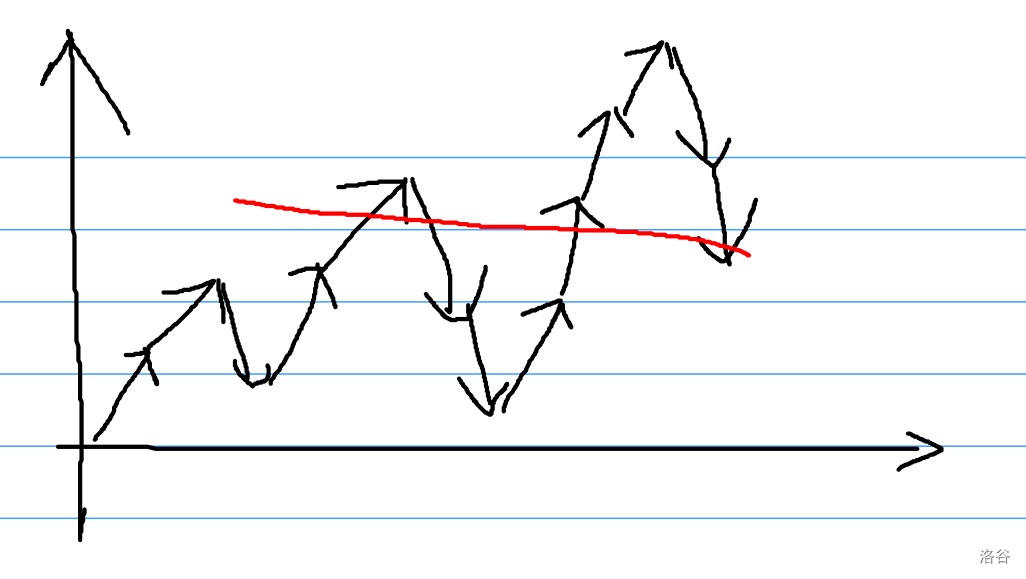
那么当该端点“突破最大值”时,一定无解,因为新的端点成为了唯一的最大值。
形式化的 $i$ 是有用的右端点的必要条件是 $\max(s_0,s_1,...,s_{i-1})
\ge s_i$。
而势能 $\max(s_0,s_1,...,s_{i-1})-s_i$ 遇到 $+1$ 会减少 $O(1)$,遇到 $-1$ 会增加 $O(1)$,那么有用的右端点个数至多 $O(B)$ 个,同理有用的左端点个数至多 $O(B)$ 个。
那么我们只要把所有关键点取出来,其他的缩成连续段即可,这里的复杂度是 $O(B\log n)$。
总复杂度为 $O(qB+\frac{n^2}{B}+qB\log n)$。$B$ 取 $\sqrt{n}$ 可以冲过去。
> 总结:
>
> - 如果存在关于出现次数,权值众数相关复杂度的暴力算法考虑按出现次数根号分治。
>
> - $\sum_i\sum_jcnt_i+cnt_j=m\times \sum_i cnt_i$。
>
> - 对于只与端点信息相关的统计问题可以考虑将有用的端点拿出来(可能很少)。
>
> - 变化连续 $+1,-1$ 可以考虑用折线图刻画,这里很重要的一点是,变化连续,因此最值通常有特殊的地位。
### P8360 [SNOI2022] 军队
[题目链接](https://www.luogu.com.cn/problem/P8360)
#### 简要题意
有一个长度为 $n$ 的序列,每个位置有一个颜色 $c_i$,以及权值 $a_i$,满足 $1\le c_i\le C$。
维护 $q$ 次操作,每次操作为以下三种之一:
- 给定 $l,r,x,y$ 将区间 $[l,r]$ 中颜色为 $x$ 的位置的颜色改成 $y$。
- 给定 $l,r,x,v$ 将区间 $[l,r]$ 中颜色为 $x$ 的位置的权值增加 $v$。
- 给第 $l,r$,查询区间 $[l,r]$ 的权值和。
$1\le n,q\le 2.5\times 10^5,1\le a_i,v\le 10^8,1\le c_i,x,y\le C$。
#### 题解
首先考虑简单的情况,所有操作 $l=1,r=n$ 怎么做。我们可以使用并查集维护一个类似树形的结构,用子树刻画某种颜色的位置。
考虑对序列分块,每个块内部维护一个这样的树形结构以及当前的区间和,除了维护整块对三种操作的支持还需要维护重构。
初始时,将块中出现的每个颜色单独建一个点,序列中每个位置是叶子节点,作为对应颜色节点的儿子。
对于对整块进行操作 $1$,如果不涉及合并两种颜色我们不用新建节点,如果合并两种颜色我们新建一个点用于合并两种颜色。
这样可以保证对于任意块维护的森林的点数是不超过 $O(B)$ 的,因为每新增一个点连通块个数减一。
对于操作 $2$ 就直接在树上打标记,维护子树内叶子个数即可更新当前块的和。
重构就直接把标记推到叶子上,清空信息即可。但是这样直接写过不了。
这里有一些实现细节:
1. 卡空间。卡常数。不能 $O(n\sqrt{n})$ 的空间,并且在线的常数比较大。但是这里每块贡献是独立的,所以可以考虑逐块处理。
2. 不能把树建出来 dfs 推标记,常数大。这里只用并查集维护,在路径压缩时处理信息合并。
更优秀的实现:
- [代码](https://www.luogu.com.cn/paste/9zvhrs0p)
- 逐块处理 `for (int L = 1, R; L <= n; L = R + 1)`
- 把并查集转化成自底向上维护内向树,用栈维护内向树的边,这样重构就把边出栈即可。
> 总结:
>
> - 分块可以对每块维护相对复杂的信息。(比如本题中的森林结构)如果 $l=1,r=n$ 存在维护比较复杂信息复杂度还可以的做法可以考虑套上分块,特别是在贡献独立时,可以很容易的迁移。
>
> - 颜色的修改合并可以使用并查集维护。
>
> - 并查集路径压缩时处理点到根的信息。(本题因为每次只会在根上操作,非根节点上的权值不会动了,所以路径压缩时可以直接把信息传下去)
>
> - 每次新增一个点连通块个数就 -1。这里的点数分析。
## 2023.1.21
### P8361 [SNOI2022] 倍增
[题目链接](https://www.luogu.com.cn/problem/P8361)
#### 简要题意
给定进制数 $B$ 和位数 $n$,求一个 $n$ 位 $B$ 进制数 $x$ 满足 $2x$ 的所有数位在 $B$ 进制下是 $x$ 的所有数位的一个排列且对于任意 $1\le i\le n$,$x$ 和 $2x$ 在 $B$ 进制下的第 $i$ 位不能同时为 $0$。如果不存则输出 $-1$。
$1\le T\le 10^4,2\le \sum B\le 2\times 10^5,1\le \sum n\le 2\times 10^5$。
#### 题解
首先应该注意到,对于固定的进制 $B$,如果存在一个符合要求的 $n$ 位 $B$ 进制数,那么一定存在一个符合要求的 $n+1$ 位的 $B$ 进制数:
- 对于 $B$ 进制下符合要求的数 $x$,$2x$ 一定是存在进位的。不然在满足 $x$ 和 $2x$ 第 $i$ 位不同时存在 $0$ 且不进位的条件下一定不符合 $2x$ 的数位在 $B$ 进制下是 $x$ 数位的排列的条件。
- 因为 $2(B-1)+1\equiv B-1\pmod{B}$ 并且 $2(B-1)+1$ 一定会向前进位,并且这样进位经过若干个 $B-1$ 的 “传递”,所以对于一个二进制数 $x$,如果在计算 $2x$ 时第 $i$ 位向第 $i+1$ 位上进 $1$,那么我们在第 $i$ 位和第 $i+1$ 位中间插入若干个 $B-1$ 满足这个 $1$ 能够被传递到原来的第 $i+1$ 位并且这些 $B-1$ 在 $2x$ 中对应的位上都是 $B-1$。
- 那么对于一个 $n$ 位的,符合要求的 $B$ 进制数 $x$ 考虑找到第 $i$ 位满足 $2x$ 存在从第 $i$ 位向第 $i+1$ 位的进位,我们在两位之间插入若干个 $B-1$ 后仍然满足条件。
- 这里举一个 $B=10$ 的例子。 $x=142857$,个位的 $7+7$ 会向前进 $1$,由 $14285$ 接收。我们在 $5$ 和 $7$ 之间插入若干个 $9$,$14285\textcolor{red}{99999}7$,那么 $14285\textcolor{red}{99999}7+14285\textcolor{red}{99999}7$ 在个位上发生的进位经过 $9$ 的传递最终还是进到 $14285$ 上。
那么对于每组询问我们只要对于进制 $B$ 构造出长度最小的符合要求的数就赢了。
打表发现对于 $B\le 30$ 的情况,最小长度都比较小。考虑暴力枚举。
考虑先确定个位的权值,注意到如果个位是 $x$,那么我们可以确定序列中的数位还有 $(2x\bmod B)$,考虑类似的用序列中的数位还有 $(2x\bmod B)$ 去继续确定更多的权值,这样类似的推出来就是排列的环分解结构。但是对于一个环,我们只确定环中的一个权值我们并不能推出环上的所有权值,因为有可能得到进位,那么我们考虑枚举环上每个位置得到的进位。那么对于一个长为 $p$ 的环我们只用枚举 $O(2^pB)$ 的情况即可确定环上所有权值的情况。
确定了环上的所有权值及其进位情况,我们还需要考虑将其往数位中填的符合要求的方案。我们只要满足我们把每个环上的权值往数位中填的结果 $x$ 满足每一位在 $2x$ 中对应的权值与环上一致即可。
而填的结果 $x$ 每一位在 $2x$ 中对应的权值与环上一致只取决于每一位是否正确受到了其需要的进位。比如我们填入的权值在枚举时钦定其恰好搜到一个进位,那么在拼出的序列中其必须恰好收到一个进位,钦定未收到进位同理。即我们只在意每个元素收到的进位情况。
而每个进位都不是凭空产生的,我们需要知道进位的产生信息才能进行转移,因此对于每个数我们考虑用一个 2bit 状态表示,例如 $10$ 表示需要(即需要从前一位获得一个进位)一个进位并且不产生进位的数。同理,有状态 $00,11,01$。
一个状态为 $00$ 的元素下一位可以接状态为 $00,01$ 的元素。。。不难发现其限制形如 a.second = b.first,我们可以将其刻画成欧拉路的模型。
考虑只有两个点,编号分别为 $0,1$ 的图。每个元素看成一条边,比如 $00$ 看成边 $0\to 0$,$10$ 看成边 $1\to 0$。那么每个合法的数按数位从低位到高位将对应的边删掉可以看成一个从 $0$ 开始在 $0$ 结束的欧拉回路的模型。即一组环合法的充要条件是其建出的图存在从 $0$ 开始在 $0$ 结束的欧拉回路。
存在欧拉回路的充要条件是弱连通且每个点入度等于出度。
从 $0$ 到 $0$ 的欧拉回路有两种情况,一种是在 $0$ 这单独打转,但是这一定是不可能的,因为该情况下只有全 $0$ 是可以的。另一种是从 $0$ 到 $1$,然后再在两个点之间转,这要求 $0$ 和 $1$ 弱连通。
而入度等于出度的限制可以看成 $01$ 的个数等于 $10$ 的个数。
那么实际上我们可以搜出所有可能的环,每搜出一个新的 (环长,$01$ 的个数减 $10$ 的个数)就用背包(包含环长的和与 $01$ 的个数减 $10$ 的个数)合并上一个新的环。这里的复杂度是 $O(p^4)$。但是注意这里需要考虑弱连通,但是注意到这里选只在 $1$ 绕的环是不优的,我们把所有只在 $1$ 绕的环扔掉后就不用额外考虑弱连通了。
DP 出找到最小的 $n$ 后输出方案即可。
## 2023.1.22
### P5323 [BJOI2019]光线
[题目链接](https://www.luogu.com.cn/problem/P5323)
#### 简要题意
当一束光打到一层玻璃上时,有一定比例的光会穿过这层玻璃,一定比例的光会被反射回去,剩下的光被玻璃吸收。
设对于任意 $x$,有 $x \times a_i\%$ 单位的光会穿过它,有 $x \times b_i\%$ 的会被反射回去。
现在 $n$ 层玻璃叠在一起,有 $1$ 单位的光打到第 $1$ 层玻璃上,那么有多少单位的光能穿过**所有** $n$ 层玻璃呢?
输出答案对 $10^9+7$ 取模的结果。
$n\le 5\times 10^5,1\le a_i\le 100,0\le b_i\le 99,1\le a_i+b_i\le 100$。
#### 题解
要求的东西可以看成透光率和反射率。因为 $x$ 单位的光射进去最终要求的值可以看成 $x$ 乘上一堆系数,而我们要求的就是 $x=1$ 的情况下的答案 $v$,当 $x=x_0$ 时的答案就是 $xv$。
手玩一下 $n=2$ 的情况,注意到这个东西可以递推,令 $f_i$ 表示将前 $i$ 个玻璃叠在一起从第一个玻璃前面打一束单位为 $1$ 的光最终穿过第 $i$ 个玻璃的量,$g_i$ 表示将前 $i$ 个玻璃叠在一起从第 $i$ 个玻璃后面打一束单位为 $1$ 的光最后反射回来的光的量。
那么:
$$
f_i=f_{i-1}a_i\sum_{k=0}^{\infty}(b_ig_{i-1})^k
$$
$$
g_i=b_i+a_i^2g_{i-1}\sum_{k=0}^{\infty}(b_ig_{i-1})^k
$$
而对于形如 $\sum_{k\ge 0}x^k$,当 $|x|<1$ 时 $\sum_{k\ge 0}x^k=\frac{1}{1-x}$。
那么:
$$
f_i=f_{i-1}a_i\frac{1}{1-b_ig_{i-1}}
$$
$$
g_i=b_i+\frac{a_i^2g_{i-1}}{1-b_ig_{i-1}}
$$
> 总结:
>
> - 手玩一些小的情况,发现可以递推。
>
> - 不要对无穷求和有恐惧。
>
> - $\sum_{k\ge 0}x^k$,当 $|x|<1$ 时 $\sum_{k\ge 0}x^k=\frac{1}{1-x}$。
## 2023.1.23
### P5330 [SNOI2019] 数论
[题目链接](https://www.luogu.com.cn/problem/P5330)
#### 简要题意
给定正整数 $P,Q,T$,大小为 $n$ 的整数集 $A$ 和大小为 $m$ 的整数集 $B$,计算有多少个小于 $T$ 的非负整数 $x$ 满足 $x\bmod P\in A,x\bmod Q\in B$。
$1\le n,m\le 10^6,1\le P,Q\le 10^6,1\le T\le 10^{18},0\le A_i<P,0\le B_i<Q$。
#### 题解
这里一开始的想法是枚举 $A_i,B_j$ 计算方程组:
$$
\left\{\begin{matrix}
x\equiv A_i\pmod {P}\\
x\equiv B_j\pmod{Q}
\end{matrix}\right.
$$
在 $[0,T)$ 范围内的整数解个数。处理的直接手段就是 exCRT,但是这里实践后发现最后转化的问题并没有好的办法处理。
但是不要忘记考虑简单,直观的刻画角度。这里方程组和题面中刻画的都可以看成集合取交的问题,我们并不一定需要引入 exCRT 来进行具体的求交(因为 exCRT 可以很简单的处理一般的线性同余方程合并,但并不一定能很好的处理本题中的问题,而通过 exCRT 转化后的问题也不太好做 =,=)。
问题可以看成所有小于 $T$ 满足 $x\bmod P\in A$ 的非负整数构成的集合与小于 $T$ 满足 $x\bmod Q\in B$ 的非负整数构成的集合取交得到的集合的大小。
对于求形如 $S\cap T$ 的问题可以考虑枚举 $x\in S$,判断是否有 $x\in T$。
那这里我们枚举 $A_i$,判断有多少个 $x\bmod P=A_i$,小于 $T$ 的非负整数 $x$ 满足 $x\bmod Q\in B$。
即有多少个 $A_i+kP\in [0,T)$ 且 $A_i+kP\bmod Q\in B$。
而 $A_i+kP\bmod Q$ 的形式很熟悉。我们可以看成环上游走模型。即有一个长为 $Q$ 的环,环上编号从 $0$ 到 $Q-1$,从 $A_i\bmod Q$ 出发,每次走 $P$ 步。划分成了 $\gcd(P,Q)$ 个子环,把每个子环拆处理即可。即每个点 $i$ 连边 $(i+P)\bmod Q$。
$k$ 的取值范围我们是很容易求的。在子环上走了若干个整环加上一个区间,前缀和即可。
> 总结:
>
> - 转化成形如求 $|S\cap T|$ 的问题。对于求形如 $S\cap T$ 的问题可以考虑枚举 $x\in S$,判断是否有 $x\in T$。
>
> - $x\bmod P=A_i$ 的刻画,几何直观,以及 $x=kP+A_i$。
>
> - $A_i+kP\bmod Q$ 刻画成环上游走模型。长为 $Q$ 的环,每次走 $P$ 步。
>
> - 长为 $n$ 的环,每次走 $k$ 步,形成了 $\gcd(n,k)$ 个长为 $\frac{n}{\gcd(n,k)}$ 的子环,$i\to (i+k)\bmod n$ 即可刻画出子环。
## 2023.1.24
### P5361 [SDOI2019]热闹的聚会与尴尬的聚会
[题目链接](https://www.luogu.com.cn/problem/P5361)
#### 简要题意
给定一张 $n$ 个点 $m$ 条边的无向简单图,要求从中选出两个点集 $S_1,S_2$ 且满足 $S_2$ 是独立集。考虑 $G$ 是保留 $S_1$ 内部点及其内部点之间所有点构成的子图,令 $p$ 为 $G$ 中点的最小度数,$q=|S_2|$,要求选出的 $S_1,S_2$ 满足:
$$
\lfloor \frac{n}{p+1} \rfloor\le q,\lfloor \frac{n}{q+1} \rfloor\le p
$$
多组数据。$1\le T\le 32,1\le n\le 10^4,1\le m\le 10^5$。
#### 题解
$\frac{n}{p+1}\le q$ 的形式不太直观,而取整不太好做变换,所以考虑把取整去掉。
$$
\lfloor \frac{n}{p+1} \rfloor\le q\Leftrightarrow \frac{n}{p+1}<q+1\Leftrightarrow n<(p+1)(q+1)
$$
对于 $\lfloor \frac{n}{q+1} \rfloor\le p$ 做类似处理也可以得到 $n<(p+1)(q+1)$。
那么我们就要让 $p,q$ 尽量大。让 $p$ 尽量大是个很典的问题([P8905 [USACO22DEC] Strongest Friendship Group G
](https://www.luogu.com.cn/problem/P8905)),用个小根堆维护每个点的度数,每次答案对小根堆堆顶取 $\max$ 后删点更新其他点的度数。
而对于 $q$ 最大是一般图的最大独立集问题,感性理解限制很松,随机排列 + 模拟退火应该能跑的很好。
但是最大独立集有一个每次把度数最小点加入独立集,删与该点有边的点的近似算法。这里的突破口是每往最大独立集加一个点,至多删除 $p+1$ 个点。那么模型可以看成,每次给 $n$ 减 $k$,$q$ 加 $1$,直到 $n=0$,而 $k$ 至多为 $p+1$。那么满足:
$$
\lfloor \frac{n}{p+1} \rfloor\le q
$$
复杂度 $O(Tn\log n)$。
> 总结:
>
> - 去掉取整,做直观的变换。$\lfloor \frac{n}{p+1} \rfloor\le q\Leftrightarrow \frac{n}{p+1}<q+1\Leftrightarrow n<(p+1)(q+1)
2023.1.25
P5371 [SNOI2019]纸牌
题目链接
简要题意
有一副纸牌。牌一共有 n 种,分别标有 1,2,...,n ,每种有 C 张。故这副牌总共有 nC 张。
三张连号的牌 (i,i+1,i+2) 或三张相同的牌 (i,i,i) 可以组成一叠。如果一组牌可以分成若干(包括零)叠,就称其为一组王牌。
你从牌堆中摸了一些初始牌。现在你想从牌堆中再挑出一些牌组成一组王牌,请问有多少种可能组成的王牌呢?答案对 998244353 取模。
两组牌相同当且仅当它们含有的每一种牌数量都相同。
#### 题解
$n\le 10^{18}$ 看起来很像矩阵快速幂优化 dp。考虑写一个 dp 先。
首先考虑枚举序列 $b$ 表示第 $i$ 种牌选了 $b_i$ 张,判定该方案是不是王牌。
注意到如果用了三次 $(i,i+1,i+2)$ 一定可以替换成 $(i,i,i),(i+1,i+1,i+1),(i+2,i+2,i+2)$。那么同一组 $(i,i+1,i+2)$ 至多使用两次。
可以写出如下的 check 方法。
```cpp
bool check(int b[]) {
for (int i = 3; i <= n; i++) {
int cnt = b[i - 2] % 3;
if (b[i - 1] < cnt || b[i] < cnt) return false;
b[i - 1] -= cnt; b[i] -= cnt;
}
if ((b[n] % 3 == 0) && (b[n - 1] % 3 == 0)) return true;
return false;
}
```
直接 dp 的状态为 $f[i,j,k]$ 表示考虑前 $i$ 种牌,check 后 $i-1$ 上剩 $j$ 张牌,$i$ 上剩 $k$ 张牌的方案数。
我们接下来考虑缩小 $j,k$ 的范围。
这里的突破口是 $j$,因为我们每次用操作都是为了把 $j$ 消成 $3$ 的倍数,而实际上我们并不需要知道 $j$ 的具体取值,我们只用知道 $j$ 模 $3$ 的结果,而存 $k$ 是为了接 $j$ 的班,那么我们只用知道 $k$ 接班后会成为几即可。即我们可以把 $k$ 替换成 $(k-j)\bmod 3$,这里 $j<3$。
这样 $f[i,j,k]$ 就可以写出 $9\times 9$ 的转移矩阵,分段矩阵快速幂即可。
复杂度 $O(9^3\times X\log n)$。
> 总结:
>
> - dp 的状态机模型。
>
> - $n$ 很大考虑矩阵快速幂。
>
> - 缩减 dp 状态,排除冗余信息。!!1
### P5415 [YNOI2019] 游戏
[题目链接](https://www.luogu.com.cn/problem/P5415)
#### 简要题意
有一个长为 $n$ 的队列,$n$ 个人组成,这 $n$ 个人编号分别为 $1,2,3,...,n$。
初始时队列按顺序为 $1,2,3,...,n$。接下来将进行若干轮游戏,每轮游戏将在队列的前 $4$ 个人中进行,称游戏开始前排在第一位的人为擂主,每轮游戏每个人赢的概率相等(即均为 $\frac{1}{4}$),输的三个人在游戏开始前的队列中的相对顺序插入到队列末尾,剩下的一个人排到第 $1$ 位成为下一轮的擂主。
当一个人连续赢了 $m$ 场游戏,称他是这个游戏的赢家。给定 $1\le k\le n$,预测编号为 $k$ 的人成为赢家的概率。
$4\le n\le 10,0\le m\le 10,1\le k\le n$。
#### 题解
正着做不太好做,考虑倒着 dp,令 $f[i,j]$ 表示当前排在 $i$ 且擂主赢了恰好 $j$ 局时最终成为赢家的概率。
边界:$f[1,m]=1,\forall 2\le i\le n,f[i,m]=0$。
如果当前是擂主,有 $\frac{1}{4}$ 的概率守擂,$\frac{3}{4}$ 的概率到 $n-2$:
$$
f[1,j]=\frac{1}{4}f[1,j+1]+\frac{3}{4}f[n-2,1]
$$
如果当前参与游戏,但不是擂主,那么有 $\frac{1}{4}$ 的概率成为擂主,如果没成为擂主依赖谁赢了:
$$
f[2,j]=\frac{1}{4}f[1,1]+\frac{1}{4}f[n-2,j+1]+\frac{2}{4}f[n-1,1]
$$
$$
f[3,j]=\frac{1}{4}f[1,1]+\frac{1}{4}f[n-1,j+1]+\frac{1}{4}f[n-1,1]+\frac{1}{4}f[n,1]
$$
$$
f[4,j]=\frac{1}{4}f[1,1]+\frac{1}{4}f[n,j+1]+\frac{2}{4}f[n,1]
$$
在等待队列中:
$$
f[i,j]=\frac{1}{4}f[i-3,j+1]+\frac{3}{4}f[i-3,1]
$$
因为状态之间有环,所以这里考虑高斯消元,复杂度 $O(n^3m^3)$。
> 总结:
>
> - 概率 dp 倒着设状态。
>
> - 有环的 dp,高斯消元。