关于前缀函数——KMP,AC 自动机学习笔记
XYstarabyss
·
·
算法·理论
鲜花
小朋友们你们好啊,我是前缀函数。不认识我没关系,在 KMP 中我又叫作 next 数组,在 AC 自动机中我又叫做 fail 指针。
几年前初学 KMP 的时候一脸懵逼,看了几个讲解 KMP 的文章和视频也感觉这玩意太抽象了,没有彻底理解。直到这几天重新拾起了这些串串算法,才觉得自己稍微更加能够触及这个玩意的妙处,于是写了这篇文章,将己愚见与大家分享。
KMP 与前缀函数
问题:给你两个字符串记为 t,s,长度分别为
我们先来思考一下朴素做法。遍历 $t$ 的所有位置作为开头,然后往后一个一个字符与 $s$ 对比,中途有字符不相等就跳过,若对比到了 $s$ 的末尾就说明匹配成功一个了。
显然,这个朴素做法时间复杂度最坏约为 $O(nm)$,不怎么好用,我们要充分利用已知信息减少无用的匹配。那么该怎么利用呢?我们来看一下这个例子。
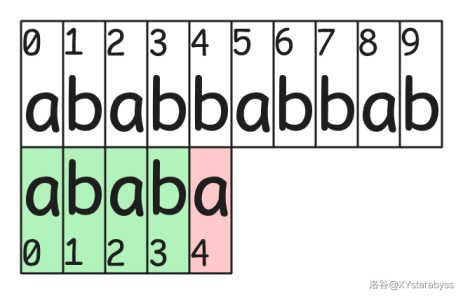
如图所示,我们的 $s$ 字符串在 $s_4$ 的位置与字符串 $t$ 失配了。那我们该怎么办呢?
首先,我们从 $t_0$ 处开始匹配 $s$ 的计划肯定是吹了,并且产生了 $4$ 次与 $t$ 串对比的沉没成本。那么我们就只能够想一想能不能收回一些这个成本。
不难想到此时我们的 $s$ 串应该往前移动,但是如果一格一格地往前移沉没成本就白花了,所以应该用之前 $s_0,s_1,s_2,s_3$ 匹配成功的信息一次往前移动 $4-x$ 格并使它前 $x$ 格与 $t$ 串匹配。$s_4$ 处失配了,没有什么能利用的信息,所以先不管。
为了方便我们利用前面匹配成功的信息,设 $r=s_0+s_1+s_2+s_3$。我们可以想一下我们想要往前移后的 $s$ 与 $t$ 匹配的前几格具有一些什么样的性质。
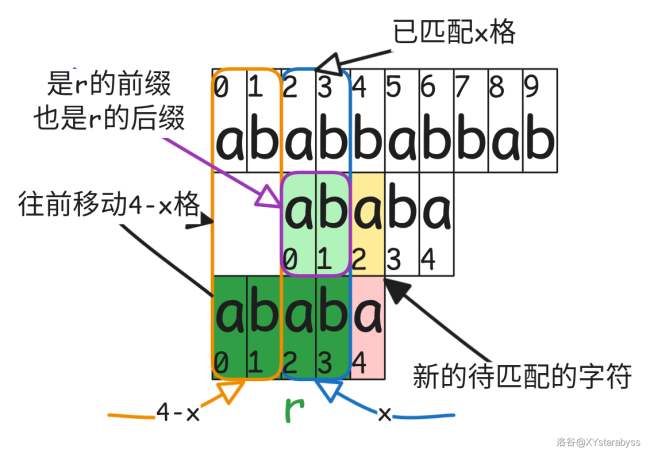
1. 它需要是 $r$ 的 **前缀**,因为无论在什么位置 $s$ 都要从 $s_0$ 开始往后与 $t$ 匹配。
2. 它还需要是 $r$ 的 **后缀**,因为我们想要利用一些 $r$ 与 $t$ 匹配成功的信息,收回一些沉没成本。
3. 它还 **不能是 $r$**,因为如果它是 $r$ 的话,那么就要保证 $r$ 与 $t$ 前四个元素全部保持匹配状态,那么 $s$ 就相当于没动。而 $s_4$ 的失配已经告诉了我们这个位置不可能匹配得到 $s$。
4. 在以上前提下,我们希望它的 $x$,即与 $t$ 匹配的位置数量尽可能的大。
综上所述,我们希望求得 $r$ 的 **最长的相等的真前缀与真后缀的长度**。其中 $r$ 的真前缀是指除了 $r$ 本身的 $r$ 的前缀,真后缀同理。
因为 $s$ 可能在任何位置突然就与 $t$ 失配了,所以我们需要所有的 $r_i=s_0,s_1,\dots,s_i\ (i\in\{0,1,2,3,4\})$ 的最长的相等的真前缀与真后缀的长度。故定义 $\pi_i$ 为 $r_i$ 的最长的相等的真前缀与真后缀的长度,这就是 ~~臭名昭著~~ 大名鼎鼎的前缀函数了。上文中的 $x$ 即为 $\pi_3$,$r$ 即为 $r_3$。
那么我们手算一下这个 $s$ 的不同 $r_i$ 对应的 $\pi_i$ 试一下。
- $r_0$:只有一个字符 $a$,很明显 $\pi_0$ 应该为 $0$。
- $r_1$:有两个字符 $ab$,因为 $ab$ 无相等的真前缀和真后缀,所以 $\pi_1$ 应该为 $0$。
- $r_2$:有三个字符 $aba$,因为真前缀 $a$ 可以和真后缀 $a$ 匹配一下,所以 $\pi_2$ 应该为 $1$。
- $r_3$:有四个字符 $abab$,因为真前缀 $ab$ 可以和真后缀 $ab$ 匹配一下,所以 $\pi_3$ 应该为 $2$。
- $r_4$:有五个字符 $ababa$,因为真前缀 $aba$ 可以和真后缀 $aba$ 匹配一下,所以 $\pi_4$ 应该为 $3$。
然后我们就可以愉快地使用 $\pi_i$ 了。
~~什么你是说怎么在电脑上面算这些 $\pi_i$,总不能 $O(m^3)$ 爆算然后比暴力还慢吧,先用着,等下再说怎么求~~
可能有眼尖的同学发现了:你这移完之后的 $s_2$ 也与 $t$ 不匹配啊,那怎么办呢?
确实匹配不了,所以我们将之后再也不要用到的 $t_0,t_1$ 略去不管,然后将它变成类似于这篇文章第一张图片的状态。
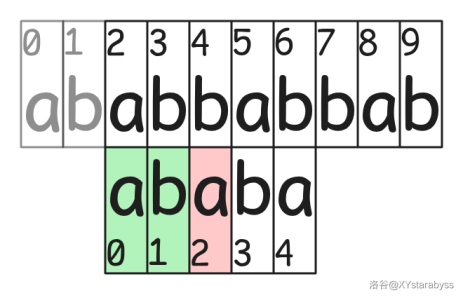
有了之前的经验,我们发现此时我们能利用的是 $r_1$,所以我们查对应的 $\pi_1$,发现是 $0$,所以这下它与 $t$ 匹配的位置数量为 $0$,得往前移动 $2$ 格,就变成了这样:
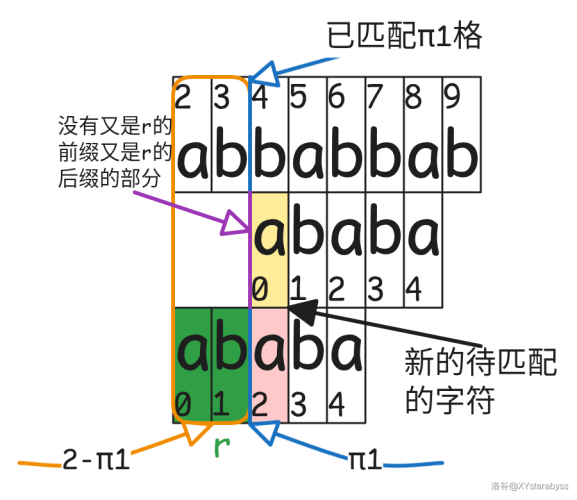
这启示我们:当我们已知 $s_0,s_1,\dots,s_{j}$ 能与 $t_{i-j-1},t_{i-j},\dots,t_{i-1}$ 匹配:
1. $s_{j+1}$ 与 $t_i$ 匹配得了,把 $s_{j+1}$ 直接扔进能与 $t$ 匹配之列,然后 `++j;`。
2. $s_{j+1}$ 与 $t_i$ 匹配不了,我们只需掏出 $\pi_j$,因为 $s_{j-\pi_j+1},s_{j-\pi_j+2},\dots,s_{j}$ 一定能与 $t_{i-\pi_j},t_{i-\pi_j+1},\dots,t_{i-1}$ 匹配,此时根据 $\pi_j$ 的定义可知 $s_0,s_1,\dots,s_{\pi_j-1}=s_{j-\pi_j+1},s_{j-\pi_j+2},\dots,s_{j}=t_{i-\pi_j},t_{i-\pi_j+1},\dots,t_{i-1}$,所以将 $j$ 赋值为 $\pi_j-1$,重复执行对 $s_{j+1}$ 与 $t_i$ 是否匹配的判断操作。
直到 $j=0$ 且 $s_{j+1}\not=t_i$,此时我们得掏出 $\pi_0$,发现此时 $0>\pi_j-1$,这就说明 $s$ 不存在前缀 $s_0,s_1,\dots,s_j$ 能与 $t_{i-j-1},t_{i-j},\dots,t_{i-1}$ 匹配的同时 $s_{j+1}=t_i$,所以 $j=\pi_0-1=-1$,就不管了。
5. 若某个执行完以上操作的时刻 $j=m-1$,说明 $s_0,s_1,\dots,s_{m-1}$ 能与 $t_{i-m},t_{i-m+1},\dots,t_{i-1}$ 匹配,此时我们就找到了一个 $t$ 中出现 $s$ 的地方。同理,若某个执行完以上操作的时刻 $j=a-1$,说明到这里为止 $s$ 有前 $a$ 位可以和 $t$ 完成匹配。
以上所有流程完成之后就可以 `++i;` 往后继续判断。
所以 KMP 就讲完了。此时来填坑算这些 $\pi_i$ 的方法。
首先,根据定义,$\pi_0$ 必定为 $0$,因为只有一个字符的字符串是没有真前缀和真后缀的。
然后,我们就发现了一个非常巧妙的事情:如果我们将 $t$ 设为 $s$,然后从 $s_1$ 开始尝试匹配,就像下面这样:
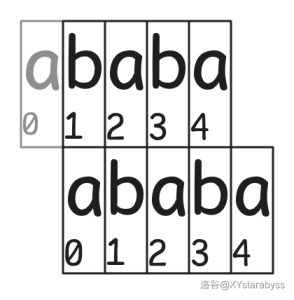
我们就会发现在 $t_i$ 处算出来的 $j+1$ 就是 $\pi_i$!
原因应该不难理解:我们发现 $s_0,s_1,\dots,s_j$ 能与 $t_{i-j},t_{i-j+1},\dots,t_{i}$ 匹配,其实际意义就相当于求最长的能与 $s_{i-j},s_{i-j+1},\dots,s_{i}$ 匹配的 $s_0,s_1,\dots,s_j$ ,前者是 $r_i$ 的前缀,后者是 $r_i$ 的后缀,而我们又不会考虑 $t_0$,即保证了后缀为真后缀;又可以发现 $s_4$ 已经位于 $t_4$ 的后面,再也匹配不到东西了,即保证了前缀为真前缀。这不就是 $r$ 的 **最长的相等的真前缀与真后缀** 吗?
又因为 $s_0,s_1,\dots,s_{j}$ 的长度为 $j+1$,所以 $j+1$ 就是 $\pi_i$。
还有一些细节需要注意一下:写 KMP 时,我们的这些字符串 $s,t$ 往往从 $1$ 开始编号,所以 $nxt$ 与 $\pi$ 还是有一些细节上的区别。具体来说,设新编号下的 $j$ 为 ${j}'$,那么所有的 ${j}'$ 都等于 $j+1$,所以 $nxt_{{j}'}=\pi_{j}$,在 $t_i$ 处算出来的 $\pi_i=j+1={j}'$,失配后 $j=\pi_j-1$ 即 $j+1=\pi_j$,所以 ${j}'=nxt
_{{j}'}$。若某个执行完以上操作的时刻 $j'=a$ 即说明 $j=a-1$,说明到这里为止 $s$ 有前 $a$ 位可以和 $t$ 完成匹配,等等。认真看了上文并且理解了的应该能够体会到这些区别。
```cpp
for(int i=1;i<=n;++i){//如果是匹配真t串就是枚举1~n,否则是2~m
while(j&&t[i]!=s[j+1]/*这就是匹配不了的重复执行判断流程*/) j=nxt[j];
if(t[i]==s[j+1]) ++j;//如果最后i匹配上j了就++j
//nxt[i]=j;//最后的这里的这个j就说明这里为止s有前j位可以和t完成匹配
}
cin>>t>>s;
n=t.length(),m=s.length();
t=" "+t,s=" "+s;//对输入进来的字符串做一些小处理
```
相信此刻大家多多少少都对 KMP 有了更加深刻的理解。那么我们宜将剩勇追穷寇,稍微思维打开一下,扩展一下前缀函数,学习——AC 自动机。
# AC 自动机
AC 自动机相比 KMP 来说就需要一定基础知识了。具体而言,您需要先学会 [【模板】字典树](https://www.luogu.com.cn/problem/P8306)。
如果您已经会了那我们就开始吧。
问题:给你一个字符串 $t$ 与一些字符串 $s_1,s_2,\dots,s_n\ (1\le n\le 2\times 10^5)$,要你回答 $t$ 出现了 $s_1,s_2,\dots,s_n$ 分别几次。
不难发现哪怕是暴力 KMP 也过不了这么多次匹配,所以我们要尝试一个能同时尝试匹配多个字符串的结构,没错它就是字典树。
首先我们先在我们这个字典树里面插入 $his,he,her,hers,is,she$ 这 $6$ 个单词,标红的节点代表它是某个单词的结尾。
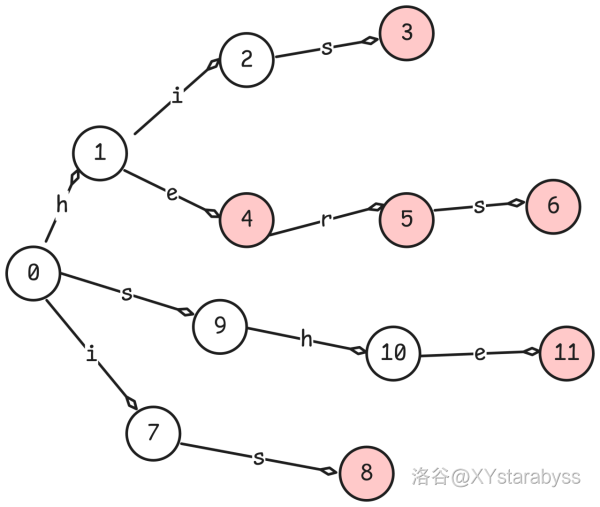
现在假设我们直接用它来匹配神秘单词 $shis$ 看看会发生什么。
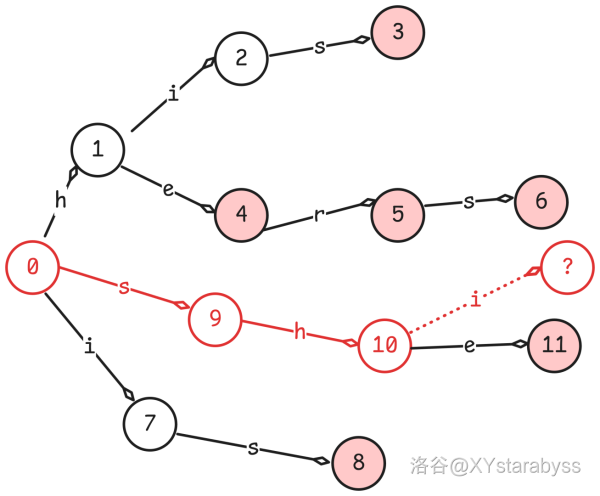
氵!我们发现 $10$ 号节点往后不存在 $i$ 边,匹配不到东西了。
这说明字典树不够用,我们需要把它扩展一下,变成字典图,让匹配转移更加完善。
具体来说,我们需要每一个点的 $h,e,i,r,s$ 边都有所指向。那么应该指向哪里呢?
首先,我们设前面匹配成功的 $sh$ 为字符串 $r$。有了前面 KMP 的思想,我们不难想到新的匹配成功的串应为 $r$ 的 **真后缀**。
但是新的匹配成功的串不一定要是 $r$ 的 **真前缀**,因为我们此时新的匹配成功的串要从 $0$ 号节点往后匹配,我们可以不钉死在 $0-9-10$ 这一条链上,还可以往其他的链去匹配其前缀,比如说 $0-1-2-3$ 这一条链。
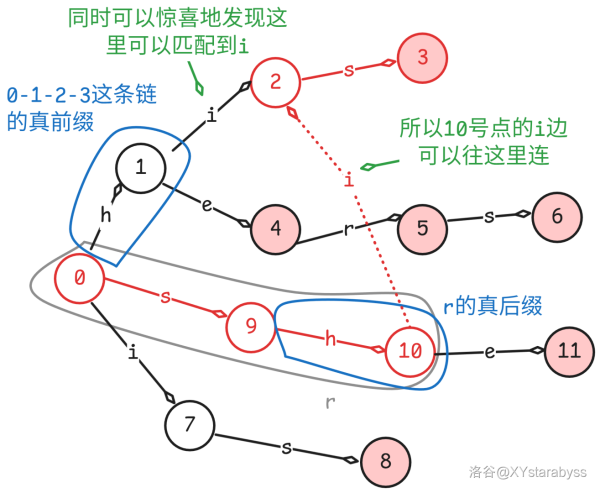
这样我们就成功匹配到了单词 $his$。注意,哪怕是 AC 自动机也和 KMP 一样,要找能往后匹配到对应字符的最长的其他条链的前缀或者该链的真前缀。
然后按照上述规则将每个点都如此操作,就可以扩展出非常好用的字典图了。如下所示:(为了不让图显得太过于凌乱,只画了与 $0$ 号节点直接相邻的节点新增的边)
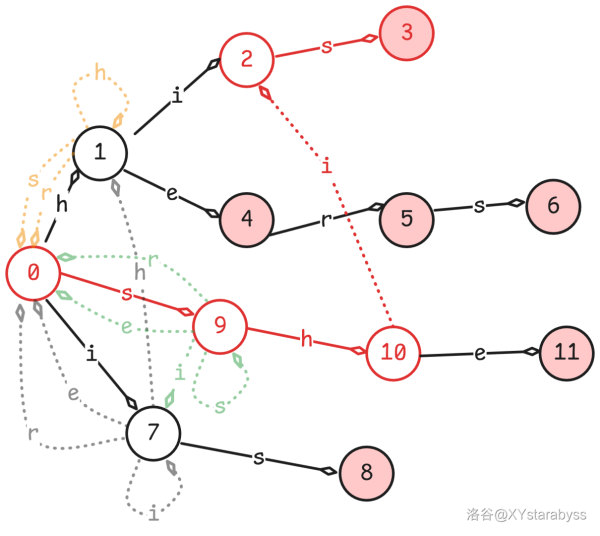
可能有同学要问了,你这个字典图暴力去求时间复杂度一点也不低啊。
所以我们的前缀函数在稍微扩展了一下之后又重新出山,变成了 $fail$ 指针!
$fail$ 指针指向 **能产生最长的相等的 $r$ 的真后缀与所有其他链中的前缀(或 $r$ 的真前缀)的末尾字符指向的那个节点** 。这就意味着类似于 KMP 中 $s_{j+1}\not=t_i$ 的情景,一直通过 $fail$ 指针跳,直到当前跳到的节点存在能与要匹配的字符匹配的边或跳到了 $0$ 号节点,这些都可以类比 KMP 的匹配过程。
那么 $fail$ 指针又该怎么求呢,好像也没有什么特别巧妙的方法,只能一步一步想,和字典图一起去构建。
首先 $0$ 号节点的 $fail$ 指针肯定指向的是自身,我们来思考一下能不能由此推出与之相连的节点的 $fail$ 指针。
参照上图,我们发现好像与之相连的节点的 $fail$ 指针指向的节点就是 $0$ 号节点,这个显然是没有什么问题的。
那其他点的 $fail$ 指针怎么求呢?以 $10$ 号点为例,我们发现它的 $fail$ 指针指向的是其父亲节点的 $fail$ 指针(即 $0$)沿 $h$ 边走一下,即 $1$ 号节点。
更普遍地,若一个节点 $i$ 沿 $x\ (x\in {a,b,\dots,z})$ 边走一下:
1. 到达节点 $j$:那么 $fail_j$ 指向的就是 $fail_i$ 沿 $x$ 边走一下对应的点。理解一下,就是利用了前面的节点的信息,后缀前缀同时加上 $x$ 字符。这个用来建造 $fail$ 指针。
2. 没有对应的节点:那么就将 $i$ 沿 $x$ 边走一下到的那个节点定为 $fail_i$ 沿 $x$ 边走一下到的那个节点。这个可以直接对应 KMP 中 $j=nxt_j$。这个用来建造字典图。
$fail$ 指针示意图:
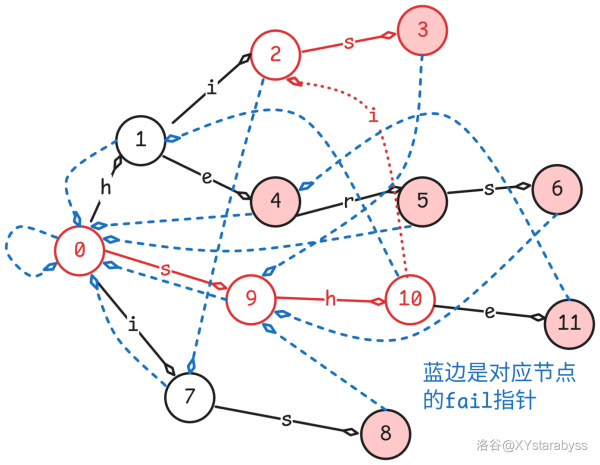
那么可能有人要问了,如果 $fail_i$ 沿 $x$ 边走一下对应的点不存在怎么办?难道只能指向 $0$ 号节点,然后破坏了我们需要的性质?
实际上,只要我们选用合适的遍历顺序,就总可以让 $fail_i$ 对应的那个节点总已经建好了所有我们需要的边和 $fail$ 指针,对应的点不可能不存在,然后我们就可以利用前面已建完的字典图来完成当前这个节点的出边扩展和 $fail$ 指针。这个遍历方式就是 bfs。这也是 AC 自动机建造不能使用 dfs,要用 bfs 的原因。
根据上文,可以比较顺畅地写出 AC 自动机的建造代码:
```cpp
#define f(n,m,i) for(register int i(n);i<=m;++i)
int tot,cnt,ans[N];
struct Node{
int s[26],fail,id;//子节点,fail指针,某字符串结尾标记
void init(){ memset(s,0,sizeof s),cnt=fl=id=0;}//初始化
}t[N];
void ins(string c,int &id){
int x(0),i(0);
while(c[++i]){//建字典树
int &y(t[x].s[c[i]-'a']);
if (!y) y=++tot,t[y].init();
x=y;
}
if (!t[x].id) t[x].id=++cnt;
id=t[x].id;//记得记录一下si结尾对应的那个点
}
void bld(){
queue<int>q;
f(0,25,i) if (t[0].s[i]) q.push(t[0].s[i]);
//加入所有直接和0相邻的节点,而不是直接加入0,因为这些节点的fail指针全指向0,
//用t[t[x].s[i]].fail=t[t[x].fail].s[i]会指向自身而出现问题,而且0号节点也不需要补充出边
while (!q.empty()){
int x(q.front());q.pop();
f(0,25,i){
if (t[x].s[i])//有对应节点就为其构建fail指针,并加入队列
t[t[x].s[i]].fail=t[t[x].fail].s[i],q.push(t[x].s[i]);
else t[x].s[i]=t[t[x].fail].s[i];//没有就补充完所有这个节点的出边
}
}
}
void ask(string c){
int x(0),i(0);
while(c[++i]){
x=t[x].s[c[i]-'a'];
for(int j(x);j;j=t[j].fail) ++ans[t[j].id];//跳fail指针找所有同时完成匹配的字符串
}
}
```
注意:完成的字典图可以看作是一个有向图,亦可在上面做一些图论操作。比如说要拓扑排序优化 AC 自动机才能过 [它最强的那个板子](https://www.luogu.com.cn/problem/P5357)。
怎么拓扑排序优化就不细讲了,不然就偏题了,这里仅略微带过:
```cpp
//记得稍微改一下上面的代码,算一下再字典图中每个点的入度
void cmp(string c){
int x(0),i(0);
while(c[++i])
x = t[x].s[c[i] - 'a'],t[x].cnt ++;
//直接把AC自动机当一般的有向图,记录字符串t在其上匹配的“路径”
}
void ask(){
queue<int>q;
f(0,tot,i) if(!t[i].rd) q.push(i);//正常拓扑排序,先加入所有入度为0的节点
while (!q.empty()){
int x(q.front()),y(t[x].fail);q.pop();
ans[t[x].id]=t[x].cnt;//若该节点对应某个(或某些)字符串的结尾,统计下对应的答案
t[y].cnt+=t[x].cnt;//同时这也匹配到了以其fail指针对应节点为结尾的字符串
if (!--t[y].rd) q.push(y);//正常拓扑排序
}
}
```
# 后记
本文的参考资料:[1](http://oi-wiki.com/string/kmp/) [2](http://oi-wiki.com/string/ac-automaton/)
鸿篇巨著,花了作者不少时间写就,希望大家点赞支持一下作者!
同时也欢迎各位奆佬指出此文的锅或讲得不怎么清楚了地方。