浅谈数学归纳法

**参考文献：《高中数学竞赛教程》。** **注：如有误请私信[黄耀风](https://www.luogu.com.cn/user/289275)，以及时修改。** ## $\texttt{Part 0}$：前言 小 Y：还记得怎么计算 $1+2+\cdots+n$ 吗？ 小 H：当然，这个式子的值就是 $\dfrac{n(n+1)}{2}$ 啊。 小 Y：那你知道怎么证明吗？虽然网上的证明十分多，但是有一种更加新奇的方式哦！ 小 H：是什么？ 小 Y：数学归纳法！ ## $\texttt{Part 1}$：什么是数学归纳法？ 数学归纳法是一种很常用的数学方法，多用于证明一些关于正整数或者非负整数 $n$ 有关的命题。 对于等差数列求和，也可以通过数学归纳法进行证明。 有一道例题如下： 设正数 $a_1,a_2,\cdots$ 构成了等差数列，请你证明： $\dfrac{1}{\sqrt{a_1}+\sqrt{a_2}}+\dfrac{1}{\sqrt{a_2}+\sqrt{a_3}}+\dfrac{1}{\sqrt{a_3}+\sqrt{a_4}}+\cdots+\dfrac{1}{\sqrt{a_{n-1}}+\sqrt{a_n}}=\dfrac{n-1}{\sqrt{a_1}+\sqrt{a_n}}$。 自己可以先想想怎么做，再往下看哦！ ## $\texttt{Part 2}$：数学归纳法的基本形式 数学归纳法一般分为以下两个步骤： 1. 将原式中的 $n$ 带入一些具体值，例如 $n=1$ 时，证明原式成立。这一步是较为简单的，**但也是必不可少的**。 2. 假设 $n=k$ 时原式成立，下一步我们要推出 $n=k+1$ 的时候原式也成立。数学归纳法难就难在这一步，因此接下来会讲解大量例题，以帮助更好的理解与运用。 ~~然后就没了。~~ 至于这个方法的原理，可以理解为多米诺骨牌。一旦第一步（假如是） $n=1$ 成立，而第二步证明了 $n=1$ 成立时，$n=2$ 也成立。结合多米诺骨牌，$n=2$ 一旦成立。便会导致 $n=3,4,\cdots$ 都成立，就如多米诺骨牌前一张推倒后一张一样。 是的，简简单单的两步，却是我们解决问题的一大利器。而第二步，更是重中之重。 怎么重呢？让我们往下看看实例： ## $\texttt{Part 3}$：数学归纳法的基本例题 先来证明等差数列求和公式，以证明 $1+2+\cdots+n=\dfrac{n(n+1)}{2}$ 为例。 首先 $n=1$ 时，$1=\dfrac{1 \times 2}{2}$，故命题成立。 假设在 $n=k$ 时，命题成立，那么在 $n=k+1$ 时，原式 $=1+2+\cdots+k+(k+1)=\dfrac{k(k+1)}{2}+(k+1)=\dfrac{(k+1)(k+2)}{2}=\dfrac{n(n+1)}{2}$。 故命题对于一切正整数 $n$ 成立。 再来讲讲 $\texttt{Part 1}$ 部分的例题吧： 我们记这个等差数列的公差为 $d$，由于数列中的每一项都是正数，所以 $d \ge0$，否则这个数列一定会有小于 $0$ 的数。如果 $d=0$ 则结论显然，易得等式成立，故以下仅对 $d >0$ 的情况进行探讨。 接下来我们按照 $\texttt{Part 2}$ 的步骤解它！ 第一步，代入特殊的 $n$ 的值。因为如果 $n=1$ 的时候等式无意义，故我们将 $n=2$ 带入等式。如果 $n=2$，那么等式的左式 $= \dfrac{1}{a_1+a_2}$，等式的右式 $= \dfrac{1}{a_1+a_2}$，明显等式成立。 第二步（敲重点！）： 我们假设当 $n=k(k \ge 2)$ 时等式已成立，则有： $\dfrac{1}{\sqrt{a_1}+\sqrt{a_2}}+\dfrac{1}{\sqrt{a_2}+\sqrt{a_3}}+\dfrac{1}{\sqrt{a_3}+\sqrt{a_4}}+\cdots+\dfrac{1}{\sqrt{a_{k-1}}+\sqrt{a_k}}=\dfrac{k-1}{\sqrt{a_1}+\sqrt{a_k}}$ 那么，当 $n=k+1(k \ge 2)$ 时，则等式左式为： $\quad \dfrac{1}{\sqrt{a_1}+\sqrt{a_2}}+\dfrac{1}{\sqrt{a_2}+\sqrt{a_3}}+\dfrac{1}{\sqrt{a_3}+\sqrt{a_4}}+\cdots+\dfrac{1}{\sqrt{a_{k-1}}+\sqrt{a_k}}+\dfrac{1}{\sqrt{a_k}+\sqrt{a_{k+1}}}$ $=\dfrac{k-1}{\sqrt{a_1}+\sqrt{a_k}}+\dfrac{1}{\sqrt{a_k}+\sqrt{a_{k+1}}}$ $=\dfrac{(k-1)(\sqrt{a_k}-\sqrt{a_1})}{(\sqrt{a_1}+\sqrt{a_k})(\sqrt{a_k}-\sqrt{a_1})}+\dfrac{\sqrt{a_{k+1}}-\sqrt{a_k}}{(\sqrt{a_k}+\sqrt{a_{k+1}})(\sqrt{a_{k+1}}-\sqrt{a_k})}$ $=\dfrac{(k-1)(\sqrt{a_k}-\sqrt{a_1})}{a_k-a_1}+\dfrac{\sqrt{a_{k+1}}-\sqrt{a_k}}{a_{k+1}-a_k}$ $=\dfrac{(k-1)(\sqrt{a_k}-\sqrt{a_1})}{[a_1+(k-1)d]-a_1}+\dfrac{\sqrt{a_{k+1}}-\sqrt{a_k}}{[a_1+kd]-[a_1+(k-1)d]}$ $=\dfrac{(k-1)(\sqrt{a_k}-\sqrt{a_1})}{a_1+(k-1)d-a_1}+\dfrac{\sqrt{a_{k+1}}-\sqrt{a_k}}{a_1+kd-a_1-kd+d}$ $=\dfrac{\sqrt{a_k}-\sqrt{a_1}}{d}+\dfrac{\sqrt{a_{k+1}}-\sqrt{a_k}}{d}$ $=\dfrac{\sqrt{a_{k+1}}-\sqrt{a_1}}{d}$ $=\dfrac{(\sqrt{a_{k+1}}-\sqrt{a_1})(\sqrt{a_1}+\sqrt{a_{k+1}})}{d(\sqrt{a_1}+\sqrt{a_{k+1}})}$ $=\dfrac{a_{k+1}-a_1}{d(\sqrt{a_1}+\sqrt{a_{k+1}})}$ $=\dfrac{(a_1+kd)-a_1}{d(\sqrt{a_1}+\sqrt{a_{k+1}})}$ $=\dfrac{k}{\sqrt{a_1}+\sqrt{a_{k+1}}}$ 通过这一系列的步骤，我们成功地将以上那个等式证明了出来。同时请注意上文的 $[]$ 仅指中括号，而非取整符号。 当然，这道题也不只有这种方法可以做出来。下面再提供一种我的同学的方法： 首先看首项 $\dfrac{1}{\sqrt{a_1}+\sqrt{a_2}}$，可以将这个式子化为 $\dfrac{\sqrt{a_1}-\sqrt{a_2}}{a_1-a_2}$。设公差为 $d$，则明显 $a_1-a_2=-d$，即原式等于 $-\dfrac{\sqrt{a_1}-\sqrt{a_2}}{d}$。将每一项都按照这个方法表示，即原式等于： $-\dfrac{\sqrt{a_1}-\sqrt{a_2}+\sqrt{a_2}-\sqrt{a_3}+ \cdots +\sqrt{a_{n-1}}-\sqrt{a_n}}{d}$，化简后得：$-\dfrac{\sqrt{a_1}-\sqrt{a_n}}{d}$ $(1)$。 因为 $(\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b})=a-b$，所以$(\sqrt{a}-\sqrt{b})=\dfrac{a-b}{\sqrt{a}+\sqrt{b}}$，所以 $(1)$ 式等于： $-\dfrac{\dfrac{a_1-a_n}{\sqrt{a_1}+\sqrt{a_n}}}{d}=-\dfrac{\dfrac{a_1-a_n}{d}}{\sqrt{a_1}+\sqrt{a_n}}=\dfrac{\dfrac{-(n-1)d}{-d}}{\sqrt{a_1}+\sqrt{a_n}}=\dfrac{n-1}{\sqrt{a_1}+\sqrt{a_n}}$。 至此，我们成功运用了两种方法做出来了这一道题。 那么问题来了——数学归纳法真的有那么玄乎吗？上面那一题想必第二种解法更容易被大众想到。 其实并非如此！ 来看一下下面一道例题： 已知 $a,b$ 为正实数，且 $\dfrac{1}{a}+\dfrac{1}{b}=1 $，求证，对于每一个 $n\in \mathbb{N}(\mathbb{N}$ 表示自然数集$)$，都有 $(a+b)^n-a^n-b^n\ge 2^{2n}-2^{n+1}$。 有头绪吗？让我们一起用数学归纳法解决这一题。 首先，当 $n=1$ 时，左式 $=0=$ 右式，知命题成立。 假设当 $n=k$ 时命题成立，即 $(a+b)^k-a^k-b^k \ge 2^{2k}-2^{k+1}$。那么当 $n=k+1$ 时， 左式 $=(a+b)^{k+1}-a^{k+1}-b^{k+1}=(a+b)[(a+b)^k-a^k-b^k]+a^kb+ab^k$。 由 $\dfrac{1}{a}+\dfrac{1}{b}=1$，得 $ab=a+b$；又因为 $(a+b)(\dfrac{1}{a}+\dfrac{1}{b})=2+(\dfrac{b}{a}+\dfrac{a}{b})\ge 4$，即知 $ab=a+b \ge 4$，这样便知： $a^kb+ab^k \ge 2 \sqrt{a^kb\times ab^k}=2\sqrt{(ab)^{k+1}} \ge 2 \times2^{k+1}=2^{k+2}$。 由此，得： 左式 $=(a+b)[(a+b)^k-a^k-b^k]+a^kb-ab^k \ge 4(2^{2k}-2^{k+1})+2^{k+2}=2^{2k+2}-2^{k+2}=$ 右式。 所以，命题得证。 怎么样？数学归纳法的神通之处就在此展现了出来。但是，它还能做更多的事！ 再来看一道例题： 假设有 $2^n$ 个球分成了若干堆，如果甲堆的球数 $a$ 小于等于乙堆的球数 $b$，那么就可以从甲中取出 $a$ 个球到乙堆。这算是挪动了一次。求证：可以经过有限次移动使这若干堆球合并成一堆。 相信大家和我一样看到这一题的第一想法就是：“这不废话吗，肯定可以啊！”但是一旦开始想要怎么表达却变的手无足措。那么，我们一起来用数学归纳法解决这一题： 首先当 $n=1$ 时，只有两个球。这时候有两种情况： - 这两个球本来就在同一堆里，那么肯定可以。 - 这两个球在两堆里，每堆各 $1$ 个球，那么就可以从第一堆取出 $1$ 个球到第二堆。 通过以上两种情况，我们知 $n=1$ 时命题是成立的。 接下来，我们假设 $n=k$ 的时候命题成立，可是当 $n=k+1$ 时，球数从 $2^k$ 到了 $2^{k+1}$，翻了一倍，我们就要想着怎么样通过 $n=k$ 推出 $n=k+1$。 首先，在 $2^{k+1}$ 所分出的若干堆球中，**一定有偶数个球数为奇数的堆**，否则球数为奇数个。我们将这些球数为奇数的堆**两两配对**，进行一次合并，那么现在所有的球堆的球数就**都是偶数**，当然也有可能有的球堆球数为 $0$。这时候，我们将每一堆的球**两两绑在一起，视为一个球**，于是，球数便成了 $2^k$，而前面又假设 $2^k$ 时成立，也就是说，总球数为 $2^{k+1}$ 的时候，命题也成立。 ~~妙啊！~~ 但是，这只是数学归纳法的**基本形式**！ 接下来，我们的题目难度将升级！ ## $\texttt{Part 4}$：数学归纳法的变通形式 所以，数学归纳法的变通形式到底有什么呢？ **一、合适的假设方式** **二、大跨度的跳跃** **三、灵活的归纳途径** 接下来，我将针对这两种变通形式，讲解题目以助于你们理解。 ### $\texttt{Part 4.1}$：数学归纳法的变通形式 之 合适的假设方式 所谓的合适的假设方式，是因为前面我们一直都是假设 $n=k$ 时命题成立去证明 $n=k+1$ 时命题成立，现在合适的假设方式，如假设 $n \leq k$ 时命题成立，去证明 $n=k+1$ 时命题也成立，即为： $$n\leq k \rightarrow n=k+1$$ 可是这样真的有用吗？我们以例题为例： 证明：任何一个真分数 $\dfrac{m}{n}$ 都可以表示为若干个**互不相同的**自然数的倒数之和。这个结论在[这道题](https://www.luogu.com.cn/problem/UVA12558)所运用。 不会？试试用数学归纳法吧！ 固然真分数 $\dfrac{m}{n}$ 可以表示为 $m$ 个 $\dfrac{1}{n}$ 的和，但是题目中要求为**互不相同的**自然数的倒数之和，所以还是用数学归纳法，对 $m$ 进行归纳较好。 首先当 $m=1$ 时，对于一切分数 $\dfrac{m}{n}=\dfrac{1}{n}$ 都可以表示为 $n$ 的倒数，故命题成立。 假设 $m \leq k$ 时命题成立，即任何分子不超过 $k$ 的分数最简分数 $\dfrac{m}{n}$ 都可以表示为 $\dfrac{1}{t_1}+\dfrac{1}{t_2}+\cdots+\dfrac{1}{t_l}$，其中 $t_1,t_2,\cdots t_l$ 互不相等。现在我们要证明对于最简分数 $\dfrac{k+1}{n}$ 时命题也成立。 由于 $0 < k+1 <n$ 且 $\gcd(k+1,n)=1(\gcd(a,b)$ 表示 $a,b$ 的最大公约数$)$，可以假设 $n=q(k+1)+r$，其中 $q,r$ 皆为正整数，且 $0<r<k+1$。 因此，便有： $\dfrac{k+1}{n}-\dfrac{1}{q+1}=\dfrac{(k+1)(q+1)-q(k+1)-r}{n(q+1)}=\dfrac{k+1-r}{n(q+1)}$。 注意到 $k+1-r<k+1$，即 $k+1-r \leq k$，因此将分数 $\dfrac{k+1-r}{n(q+1)}$ 化简后其分子不超过 $k$。 故可知它可以表示为若干个互不相同的倒数之和，即 $\dfrac{k+1}{n}=\dfrac{1}{q+1}+\dfrac{k+1-r}{n(q+1)}=\dfrac{1}{q+1}+\dfrac{1}{s_1}+\dfrac{1}{s_2}+\cdots+ \dfrac{1}{s_{v}}\qquad (1)$。 现在只需要证明 $q+1 \notin \{s_1,s_2,\cdots,s_v\}$ 即可。 考虑反证法，假设 $q+1 \in \{s_1,s_2,\cdots,s_v\}$： $\dfrac{1}{q+1}+\dfrac{1}{s_1}+\dfrac{1}{s_2}+\cdots +\dfrac{1}{s_v} \ge \dfrac{2}{q+1}=\dfrac{2n}{(q+1)(k+1)}·\dfrac{k+1}{n}=\dfrac{2q(k+1)+2r}{(q+1)(k+1)}·\dfrac{k+1}{n}\ge (\dfrac{2q}{q+1}+\dfrac{2r}{(q+1)(k+1)})·\dfrac{k+1}{n}>\dfrac{k+1}{n}\qquad(2)$。 比较 $(1),(2)$ 两式，即可得出矛盾。 故对于一切分子为 $k+1$ 的正真分数命题成立，因此对于一切的正真分数命题都成立。 这就是选择合适的假设方式的优点！ ### $\texttt{Part 4.2}$：数学归纳法的变通形式 之 大跨度的跳跃 我们之前的证明都是类似：假设 $n=k$ 时命题成立，证 $n=k+1$ 时命题也成立。现在不一样了。 举个例题： 证明对于一切的正整数 $n \ge 3$，可以将一个正三角形分成 $n$ 个等腰三角形。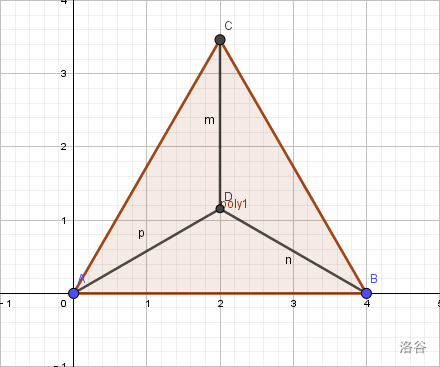 考虑 $n=3,4$ 时，有如下的构造方案： $P_1$ 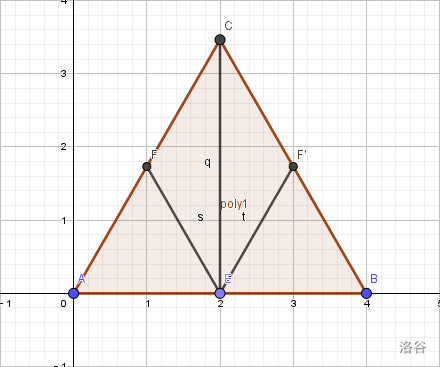$P_2$ 考虑如果跨度为 $1$，即能够从 $n=k$ 到 $n=k+1$ 来证明，能否构造呢？ 答案是显然的： $P_3$ 对于 $n=3,4,5$，可以依次按照上面的 $P_1,P_2,P_3$ 构造。我们注意到，在 $n=5$ 时构造出了一个等腰直角三角形。于是，我们每次可以做这个直角三角形斜边上的中线，便每次都可以多构造出一个等腰三角形，于是命题对于一切正整数 $n \ge3$ 成立。 那么，我们如何做到“大跨度”的跳跃呢？ 在返回看 $P_1$ $P_2$ 对于这两个构造方法，我们发现都出现了顶角为 $120^{\circ}$ 的等腰三角形，而对于一个顶角为 $120^{\circ}$ 的等腰三角形，我们可以用如下方法使其分为 $3$ 个等腰三角形： $P_4$。 于是，对于 $n=3$ 的构造，我们可以将 $120^{\circ}$ 的等腰三角形如上处理，便可以得到 $n=5,7,\cdots$ 的构造；对于 $n=4$ 的构造，我们可以将 $120^{\circ}$ 的等腰三角形如上处理，便可以得到 $n=6,8,\cdots$ 的构造。因此，命题对于一切正整数 $n \ge3$ 成立。 这个证法是跨度为 $2$。当然，跨度为 $3$ 也是可以构造的，这里不过多说明，请读者自行思考。 由此可见，大跨度的跳跃也是一种使用数学归纳法的利器。 ### $\texttt{Part 4.3}$：数学归纳法的变通形式 之 灵活的归纳途径 由于这是灵活的归纳途径，因此光靠文字很难说明清楚，下面来看一道例题： 设 $a_1<a_2< \cdots<a_n$，而 $b_1,b_2,\cdots,b_n$ 是 $a_1,a_2,\cdots,a_n$ 的一个排列。已知 $a_1+b_1<a_2+b_2< \cdots <a_n+b_n$，求证：对于一切的 $i(1 \leq i \leq n)$，满足 $b_i=a_i$。 对于这个问题，想要直接证明每个 $b_i$ 都等于相对应的 $a_i$ 是很难实现的。所以我们先考虑这么一个结论：至少存在一个 $i_0$，满足 $b_{i_0}=a_{i_0}$。考虑使用反证法和数学归纳法来证明这个结论。 反证：假设对于任意的 $i(1 \leq i \leq n)$，都有 $b_i\neq a_i$，于是 $b_1 \neq a_1$。但是由于 $a_1$ 是集合 $\{a_1,a_2,\cdots,a_n\}$ 中最小的元素，而 $b_1$ 也是该集合中的元素，故 $b_1>a_1$。 假设对于每个 $i \leq j$，都有 $b_i \ge a_i$，我们来证明一定也有 $b_{j+1}>a_{j+1}$。因为如果不然，有 $b_{j+1} \leq a_{j+1}$，则因我们已设对每个 $i$，都有 $b_i \neq a_i$，故知 $b_{j+1}<a_{j+1}$，因而也有 $b_{j+1} \leq a_j$（因为 $a$ 单调递增）。同理可知，由 $b_j>a_j$，得 $b_j \ge a_{j+1}$。于是，我们就有 $a_{j+1}+b_{j+1} \leq b_j+a_j$，但这明显与已知条件不符。所以 $b_{j+1}>a_{j+1}$。 从上面得分析得知，在“对于任意的 $i(1 \leq i \leq n)$，都有 $b_i\neq a_i$”的条件下，我们用数学归纳法证明了“对于一切 $i$，都有 $b_i>a_i$”，而这又显然是错误的，因为 $a_n$ 已经是最大值，不存在任何 $i$ 满足 $b_i>a_i$。因此我们假设的前提是错误的。故知存在某个数 $i_0$，满足 $b_{i_0}=a_{i_0}$。 有了上面的推理，我们可以正式开始证明我们的命题了： 当 $n=1$ 时，显然 $b_1=a_1$，故命题成立。假设 $n=k$ 时命题成立，要证当 $n=k+1$ 时命题也成立： 我们先将一开始的结论运用到 $a_1,a_2,\cdots,a_{k+1}$ 及其排列 $b_1,b_2,\cdots,b_{k+1}$ 中，由上面的结论可知存在一个数 $i_0$ 满足 $b_{i_0}=a_{i_0}$。那么对于剩下的 $k$ 个数，我们就可以用前面的归纳假设（即：“设 $n=k$ 时命题成立”）来证明。于是，命题在 $n=k+1$ 时也成立。 故知，对于一切正整数 $n$，命题都成立。 是不是开始有难度了？接下来难度还会再升一级！ ## $\texttt{Part 5}$：数学归纳法应用中的命题转化 命题转化，是再数学证明过程中常用手法。这里仅介绍在数学归纳法中的命题转化。 先来看一道题： 若 $n$ 个正角 $\alpha_1+\alpha_2+\cdots+\alpha_n=\pi$，证明： $$\sin\alpha_1+\sin\alpha_2+\cdots+\sin\alpha_n \leq n \sin \dfrac{\pi}{n}$$ 在这里，显然 $n=1$ 时上式两端相等，即命题成立。如果按照以往的解题过程： 假设 $n=k$ 时命题成立。现在如果要证明 $n=k+1$ 时也成立，就会发现一个问题： $n=k$ 时结论成立，条件是 $\alpha_1+\alpha_2+\cdots+\alpha_k=\pi$，然而对于 $n=k+1$ 时，条件变为 $\alpha_1+\alpha_2+\cdots+\alpha_{k+1}=\pi$，二者条件不同，因此不能直接使用数学归纳法。 因此，我们考虑转化命题。具体地，我们可以考虑证明： 若 $n$ 个正角 $\alpha_1+\alpha_2+\cdots+\alpha_n\leq\pi$，证明： $$\dfrac{1}{n}(\sin\alpha_1+\sin\alpha_2+\cdots+\sin\alpha_n) \leq \sin \dfrac{\alpha_1+\alpha_2+\cdots+\alpha_n}{n}$$ 这个命题不仅可以证明原来的命题，同时也便于我们使用数学归纳法。那就让我们来试一下吧！ 首先 $n=1$ 时，命题显然成立。为了方便后面的证明，接下来再看一下 $n=2$ 时的情形： 设正角 $\alpha_1+\alpha_2 \leq \pi$，于是就有 $\sin(\dfrac{\alpha_1+\alpha_2}{2}) \ge 0$，因而知： $(\sin \alpha_1+\sin\alpha_2)-2 \sin \dfrac{\alpha_1+\alpha_2}{2}$ $=2 \sin \dfrac{\alpha_1+\alpha_2}{2}\cos\dfrac{\alpha_1-\alpha_2}{2}-2 \sin \dfrac{\alpha_1+\alpha_2}{2}$ $=2 \sin \dfrac{\alpha_1+\alpha_2}{2}(\cos\dfrac{\alpha_1-\alpha_2}{2}-1)\leq 0$， 即 $\dfrac{1}{2}(\sin \alpha_1+\sin\alpha_2) \leq \sin\dfrac{\alpha_1+\alpha_2}{2}$。因此 $n=2$ 时命题也成立。 假设 $n \leq k$ 时命题也成立，即当正角 $\alpha_1+\alpha_2+\cdots+\alpha_n\leq \pi$ 且 $n\leq k$ 时，有 $$\dfrac{1}{n}(\sin\alpha_1+\sin\alpha_2+\cdots+\sin\alpha_n) \leq \sin\dfrac{\alpha_1+\alpha_2+\cdots+\alpha_n}{n}$$ 要证明命题在 $n=k+1$ 时也成立。 我们分两种情况来讨论： - $k+1=2m$ 为偶数。 则当 $\alpha_1+\cdots+\alpha_m+\alpha_{m+1}+\cdots+\alpha_{2m} \leq \pi$ 时。有 $\alpha_1+\alpha_2+\cdots+\alpha_{m} \leq \pi$ 及 $\alpha_{m+1}+\cdots+\alpha_{2m}\leq \pi$，于是由归纳假设可知： $\dfrac{1}{k+1}(\sin \alpha_1+\cdots+\sin\alpha_{k+1})$ $=\dfrac{1}{2}[\dfrac{1}{m}(\sin\alpha_1+\cdots+\sin\alpha_{m})+\dfrac{1}{m}(\sin\alpha_{m+1}+\cdots+\sin\alpha_{2m})]$ $\leq\dfrac{1}{2}[\sin\dfrac{\alpha_1+\cdots+\alpha_{m}}{m}+\sin\dfrac{\alpha_{m+1}+\cdots+\alpha_{2m}}{m}]$。 再看 $n=2$ 时的结果可知： 上式 $\leq \sin\dfrac{1}{2}(\dfrac{\alpha_1+\cdots+\alpha_{m}}{m}+\dfrac{\alpha_{m+1}+\cdots+\alpha_{2m}}{m})$ $=\sin\dfrac{\alpha_1+\cdots+\alpha_m+\alpha_{m+1}+\cdots+\alpha_{2m}}{2m}$ $=\sin\dfrac{\alpha_1+\cdots+\alpha_{k+1}}{k+1}=$ 右式。 知 $k+1$ 为偶数时命题成立。 - $k+1=2m+1$ 为奇数。 则当 $\alpha_1+\cdots+\alpha_m+\alpha_{m+1}+\cdots+\alpha_{2m+1}\leq \pi$ 时，要么 $\alpha_1+\cdots+\alpha_m \leq \dfrac{\pi}{2}$，要么 $\alpha_{m+1}+\cdots+\alpha_{2m+1}\leq \dfrac{\pi}{2}$。不妨假设 $\alpha_{m+1}+\cdots+\alpha_{2m+1}\leq \dfrac{\pi}{2}$，于是就有 $\alpha_1+\cdots+\alpha_m+\alpha_{m+1}\leq \pi$ 及 $\alpha_{m+2}+\cdots+\alpha_{2m+1}+\dfrac{\alpha_1+\cdots+\alpha_{2m+1}}{2m+1} \leq \pi$。 从而知有 $\dfrac{1}{k+2}(\sin \alpha_1+\sin\alpha_2+\cdots+\sin\alpha_{k+1}+\sin\dfrac{\alpha_1+\alpha_2+\cdots+\alpha_{k+1}}{k+1})$ $=\dfrac{1}{2}[\dfrac{1}{m+1}(\sin\alpha_1+\cdots+\sin\alpha_{m+1})+\dfrac{1}{m+1}(\sin \alpha_{m+2}+\cdots+\sin \alpha_{2m+1})+\sin\dfrac{\alpha_1+\cdots+\alpha_{2m+1}}{2m+1}]$ $\leq \dfrac{1}{2}[\sin\dfrac{\alpha_1+\alpha_2+\cdots+\alpha_{m+1}}{m+1}+\sin\dfrac{\alpha_{m+2}+\cdots+\alpha_{2m+1}+\dfrac{\alpha_1+\cdots+\alpha_{2m+1}}{2m+1}}{m+1}]$ $\leq \sin[\dfrac{1}{2} \times \dfrac{(\alpha_1+\cdots+\alpha_{m+1})+(\alpha_{m+2}+\cdots+\alpha_{2m+1}+\dfrac{\alpha_1+\cdots+\alpha_{2m+1}}{2m+1})}{m+1}]$ $=\sin\dfrac{\alpha_1+\cdots+\alpha_{2m+1}}{2m+1}=\sin\dfrac{\alpha_1+\cdots+\alpha_{k+1}}{k+1}$。 再消去上式两端的同类项，即得 $$\dfrac{1}{k+1}(\sin\alpha_1+\sin\alpha_2+\cdots+\sin\alpha_{k+1})\leq \sin\dfrac{\alpha_1+\alpha_2+\cdots+\alpha_{k+1}}{k+1}$$ 知当 $k+1$ 为奇数时命题也成立。 故对于一切自然数 $n$，当正角 $\alpha_1+\alpha_2+\cdots+\alpha_n\leq\pi$，都有 $\sin\alpha_1+\sin\alpha_2+\cdots+\sin\alpha_n \leq n \sin \dfrac{\alpha_1+\alpha_2+\cdots+\alpha_n}{n}$。 特别地，当 $\alpha_1+\alpha_2+\cdots+\alpha_n=\pi$ 时，便有 $\sin \alpha_1+ \cdots+\sin\alpha_n \leq n \sin \dfrac{\pi}{n}$，而这正是我们所希望证明的结论。 对于以上的证明过程，我们将其称为“**主动加强命题**”。我们再来看几道例题，以助于理解： 已知 $a_1=1,a_2=2$，对于 $a_{n+2}$： - 如果 $a_n \times a_{n+1}$ 为偶数，则 $a_{n+2}=5a_{n+1}-3a_n$； - 如果 $a_n \times a_{n+1}$ 为奇数，则 $a_{n+2}=a_{n+1}-a_n$。 求证对于一切的 $n \in \mathbb{N}$，$a_n \neq0$。 这一题，如果直接证明其不为 $0$，虽然我们知道 $a_1,a_2$ 不为 $0$，而且也可以假设 $a_k,a_{k+1}$ 都不为 $0$，却无法推出 $a_{k+2}$ 也不会 $0$。所以，我们需要考虑转化一下命题。但是怎么转化呢？ 先列出这个数列的前面若干项： $$1,2,7,29,22,23,49,26,-17\cdots$$ 不难发现，这些数中都没有 $4$ 的倍数！于是我们将这个数列变为除以 $4$ 后的余数，则变成了： $$1,2,3,1,2,3,1,2,3\cdots$$ 这个数列的规律就特别明显了！于是我们可以猜测，是否对于一切的自然数 $n$，满足： $$a_{3n-2}\equiv1(\mod4),a_{3n-1}\equiv2(\mod4),a_{3n}\equiv3(\mod4)$$ 既然有这样的猜测，不妨来证明一下： 首先 $n=1$ 时，$a_{1}=1\equiv1(\mod4),a_{2}=2\equiv2(\mod4),a_{3}=7\equiv3(\mod4)$，从而我们的猜想在 $n=1$ 时成立。 假设 $n=k$ 时我们的猜想成立，即 $a_{3k-2}\equiv1(\mod4),a_{3k-1}\equiv2(\mod4),a_{3k}\equiv3(\mod4)$，于是： $$a_{3k+1}=5a_{3k}-3a_{3k-1}\equiv15-6=9\equiv1(\mod4)$$ $$a_{3k+2}=a_{3k+1}-a_{3k}\equiv1-3=-2\equiv2(\mod4)$$ $$a_{3k+3}=5a_{3k+2}-3a_{3k+1}\equiv10-3=7\equiv3(\mod4)$$ 这就说明了，在 $n=k+1$ 时命题也成立。故我们的猜想对一切的 $n\in \mathbb{N}$ 都成立。所以这个数列中不含有 $4$ 的倍数。 那么，既然这个数列中不含有 $4$ 的倍数，而 $0$ 是 $4$ 的倍数，这就说明了：对于任意的 $n\in \mathbb{N}$，满足 $a_n \neq0$。我们的结论成立。 ## $\texttt{Part 6}$：数学归纳法的练习 介绍了这么多题，你应该会用了吧！现在来做几道习题练练手吧！ - 已知 $a_1=a_2=1,a_{n+2}=\dfrac{a_{n+1}^2+2}{a_n}$。求证：对于一切的 $n \in\mathbb{N}$，$a_n$ 皆为整数。 用两次数学归纳法，待定系数法，找到除了原递推方式的第二种递推方式。 - 关于斐波那契数列： > 1. 已知 $a _1=a_2=1,a_n=a_{n-1}+a_{n-2}$。求证当 $n \ge 3$ 时，对于一切的 $m \in \mathbb{N}$，满足 $a_{5m}$ 是 $5$ 的倍数。 根据递推是，从余数讨论。 > 2. 证明：每一个自然数都或是斐波那契数列中的一项，或是其中的若干项之和。 有意思的是，在[这道题](https://www.luogu.com.cn/problem/P4133)中就运用到了这个结论。可采用类似于 $n \leq k$ 的归纳形式。 - 证明：对于互不相等的自然数 $a_1,a_2,\cdots,a_n$，不等式 $(a _1^7+a_2^7+\cdots+a_n^7)+(a_1^5+a_2^5+\cdots+a_n^5) \ge 2(a_1^3+a_2^3+\cdots+a_n^3)^2$ 成立。并考虑等号何时成立。 考虑使用公式：$1^3+2^3+\cdots+n^3=\left[\dfrac{n(n+1)}{2}\right]^2$，可以列出若干个不等式进行相加。 - 证明，对于一切 $n \in \mathbb{N}$，方程 $x^2+y^2=z^n$ 一定有正整数解。 考虑调整跨度，在 $n=1$ 和 $n=2$ 时列举情况后，以 $2$ 的跨度进行分析，就可以遍历到所有正整数。 当然还有个做法是使用复数以及构造，这里就不过多赘述。 - 将一个正整数 $n$ 分解为 $a_1+a_2+\cdots+a_k$，其中 $a_1,a_2,\cdots,a_k$ 为可以相等的正整数。如果 $\dfrac{1}{a_1}+\dfrac{1}{a_2}+\cdots+\dfrac{1}{a_k}=1$，则称这个正整数 $n$ 是“完美”的。已知 $33$ 到 $73$ 的正整数都是“完美”的。求证：每一个不小于 $33$ 的正整数都是“完美”的。 假设 $33 \leq n \leq k$ 时 $n$ 是“完美”的，证明 $33 \leq n \leq 2k$ 也是“完美”的。 - 证明：对任何 $n \in \mathbb{N}$，都存在 $m \in\mathbb{N}$，使得 $(\sqrt{2}-1)^n=\sqrt{m}-\sqrt{m-1}$。 转化命题，变为证明：对任何的 $n \in \mathbb{N}$，存在 $a,b \in \mathbb{N}$，使得 $(1- \sqrt{2})^n=\sqrt{a^2}-\sqrt{2b^2},a^2-2b^2=(-1)^n$。 - 设 $a,b,c$ 是方程 $x^3-x^2-x-1=0$ 的 $3$ 个根。证明： $(1)$ $a,b,c$ 互不相同。 $(2)$ $\dfrac{a^{1989}-b^{1989}}{a-b}+\dfrac{b^{1989}-c^{1989}}{b-c}+\dfrac{a^{1989}-c^{1989}}{a-c}$ 是整数。 对于第一个问，用韦达定理以及反证法即可。 对于第二个问，证明对于一切的 $n \in \mathbb{N}$，$f(n)=\dfrac{a^{n}-b^{n}}{a-b}+\dfrac{b^{n}-c^{n}}{b-c}+\dfrac{a^{n}-c^{n}}{a-c}$ 都是整数。找到递推式，进行假设，即可证明。 ## $\texttt{Part 7}$：结语 这篇博客几个月前其实就写了一半，最近也花了好久的心思编辑而成。如果能够投入日报，那自然是不胜荣幸；如果因为一些原因没有选上，我就将其作为学习笔记，可以供大家参考和使用。 如果有任何问题，可以私信我或者在博客下方留言，我会在第一时间进行解答！