柏拉图的五种元素
一只书虫仔
·
·
个人记录
今天我们来聊聊基本几何图形。
棱柱
棱柱的相关概念
有两个面互相平行,其余各面都是四边形,且任意相邻的两个四边形的公共边都互相平行的多面体叫棱柱。互相平行的两个面叫棱柱的底面,其它各面叫棱柱的侧面,相邻两个侧面的公共边叫做棱柱的侧棱,底面多边形的顶点叫做棱柱的顶点,不在同一个面上的两个顶点的连线叫做棱柱的对角线,两个底面间的距离叫做棱柱的高。
棱柱的分类
侧棱和底面不垂直的棱柱叫做斜棱柱,侧棱与底面垂直的棱柱叫做直棱柱,底面是正多边形的直棱柱叫做正棱柱。底面是n边形的棱柱叫做n棱柱,其中四棱柱是一种我们非常常见的棱柱,当四棱柱的底面是平行四边形时,我们称它为平行六面体;底面是矩形的直四棱柱叫做长方体;所有棱长都相等的长方体叫做正方体。
初中时候简单的长方体与正方体定义去哪里了\qwq
棱柱的性质
棱柱的侧面都是平行四边形;棱柱的底面及平行于底面的截面是全等的多边形。
直棱柱的性质
直棱柱的侧面都是矩形;直棱柱的侧棱与高相等。而正棱柱的侧面都是全等的矩形。
棱锥
棱锥的相关概念
有一个面是多边形,其余各面都是有一个公共顶点的三角形的多面体叫做棱锥。棱锥中有公共顶点的各三角形,叫做棱锥的侧面;各侧面的公共顶点叫做棱锥的顶点;相邻两侧面的公共边叫做棱锥的侧棱;多边形叫做棱锥的底面;顶点到底面的距离,叫做棱锥的高。棱锥用表示顶点和底面各顶点的字母或者用表示顶点和底面的一条对角线端点的字母来表示。
棱锥的分类
底面是n边形的棱锥称为n棱锥,其中三棱锥又称为四面体。如果棱锥的底面是正多边形,且它的顶点在过底面中心且与底面垂直的直线上,则这个棱锥叫正棱锥。正棱锥侧面三角形底边上的高称为斜高。其中底面边长等于侧棱长的正三棱锥叫正四面体。
棱锥的性质
棱锥被平行于底面的平行所截,则:
$2.$侧面与底面是相似多边形;
$3.$截面面积与底面面积之比等于顶点到底面的距离的平方比。
### 正棱锥的性质
$1.$侧棱都相等,侧面都是全等的等腰三角形,斜高都相等,对角面也是等腰三角形;
$2.$有四个直角三角形,三边分别由:“高、侧棱、外接圆半径”,“高、斜高、内切圆半径”,“侧棱、斜高、底面边长的一半”,“外接圆半径、内切圆半径、底面边长的一半”构成;其中,内切圆与外接圆都是棱锥底面的正多边形的。
## 棱台
### 棱台的相关概念
用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做**棱台**。原棱锥的底面和截面分别叫做棱台的**下底面**和**上底面**,其它各面叫做棱台的**侧面**。相邻两个侧面的公共边叫做**侧棱**,上下底面之间的距离叫做棱台的**高**。
### 棱台的分类
由$n$棱锥所截得的棱台叫做$n$棱台,由正棱锥截得的棱台叫做**正棱台**,其中正棱锥的斜高被截后的部分称为正棱台的**斜高**。
### 正棱台的性质
$1.$上下底面及平行于底面的截面是相似的正多边形;
$2.$侧棱都相等,侧面都是全等的等腰梯形,斜高都相等,,对角面也是等腰梯形;
$3.$有三个直角梯形,分别由“高、上下底面的外接圆半径、侧棱”,“高、上下底面的内切圆半径、斜高”,“侧棱,斜高,上下底面边长的一半”构成,此外还有两个直角三角形,分别由上下底面的“外接圆半径、内切圆半径、底面边长的一半”构成。
## 圆柱
### 圆柱
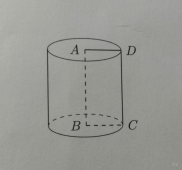
将矩形$ABCD$绕它的一边$AB$所在的直线旋转一周形成的几何体叫做**圆柱**。其中线段$AD,BC$旋转而成的曲面叫做圆柱的**侧面**,$CD$在旋转过程中形成的先都叫做圆柱侧面的**母线**,圆柱底面间的距离叫做圆柱的**高**,高与母线长相等。经过圆柱轴的截面叫做圆柱的**轴截面**,圆柱的轴截面是全等的矩形。
## 圆锥
### 圆锥
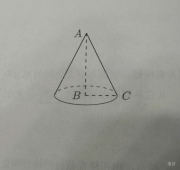
将直线三角形$ABC$绕着它的一条直线边$AB$所在直线旋转一周形成的几何体叫做**圆锥**,其中$AB$所在直线叫做圆锥的**轴**,点$A$叫做圆锥的**顶点**,直角边$BC$旋转而成的圆面叫做圆锥的**底面**,斜边$AC$旋转而成的曲线叫做圆锥的**侧面**,$AC$在旋转过程中形成的线都叫做圆锥的**母线**,圆锥顶点到底面间的距离叫做圆锥的**高**。经过圆锥轴的截面叫做圆锥的**轴截面**,圆锥的轴截面都是全等的等腰三角形。
## 球
### 球
~~球♂?~~
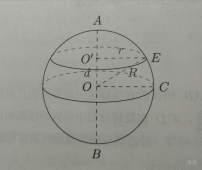
将圆心为$O$的半圆绕其直径$AB$所在的直线旋转一周形成的几何体叫做**球**。半圆的圆弧所形成的的曲面叫做**球面**,点$O$叫做**球心**,点$O$到球面上任意一点的连线称为**球的半径**,球面上两点的连线称为球的**弦**,过球心的弦被称为**直径**。任意一个平面与球面相交截面的图形为圆(也可以退化为一个点),称为**截面圆**,且球心与截面圆的圆心连线与截面垂直。
如果用$R$表示球的半径,用$r$表示截面圆的半径,则有$d=\sqrt{R^2-r^2}$,其中$d$是球心到截面的距离,即球心与圆心的连线的长度。当截面圆经过圆心时,所得到的圆称为**大圆**,其它圆被称为**小圆**。~~多直接啊~~ 如果把地球近似看成球体,那么两条经线构成一个完整的圆时,都是大圆;除赤道外,纬线圈都是小圆。~~扩充地理知识~~
好,今天我们就聊到这里。