Xor Hashing 学习笔记
wangyishan
·
·
算法·理论
XOR Hashing 学习笔记
异或的性质
异或 xor 运算是一个很奇妙的东西。更具体地说,它具有以下三条性质:
-
x\oplus x = 0
这意味着如果一个数在区间内出现了偶数次,那么最后的贡献就是 0。
-
x\oplus 0 = 0
这意味着 0 是异或运算中的单位元。
-
x \oplus y = y \oplus x,x\oplus y \oplus z = x\oplus (y\oplus z)
异或具有交换律、结合律。
什么是 XOR Hashing
异或哈希(Xor Hashing),是一种利用异或操作的特殊性和哈希降低冲突的原理,快速寻找一些神秘的东西的哈希。
知道你们看不懂,上例题:
例题一
你有一个长度为 n 的数组 a_1,a_2,\dots,a_n,保证 \forall i \in [1,n],1\leq a_i \leq n。
现在有 Q 次询问,每次询问一个区间 [l,r], 问这个区间内 a_l,a_{l+1},\dots,a_r 是否构成一个从 1 到 r-l+1 的排列。
例题一 solution
首先我们注意到区间的顺序是无所谓的,我们只需要考虑区间内每个数出现的个数。
那么注意到异或具有交换律,即无论如何交换运算顺序,结果都相同。如果我们通过判断 a_l\oplus a_{l+1} \oplus \dots \oplus a_r 是否等于 1\oplus 2 \oplus \dots \oplus (r-l+1) 来判断这两个区间是否相等行不行?
不行!显然可以举出反例:1\oplus 2 = 5\oplus 6,但是(1,2)\neq(5,6)。
那么该怎么办呢?
下面就是 xor hashing 最精辟的部分:
考虑给 1 到 n 的每个数赋一个随机权值 c_1,c_2,\dots,c_n, 每次查询时判断 c_{a_l}\oplus c_{a_{l+1}} \oplus \dots \oplus c_{a_r} 的值是否等于 c_1\oplus c_2\oplus \dots \oplus c_{r-l+1},如果等于我们就可以认为a_l,a_{l+1},\dots,a_r 构成一个从 1 到 r-l+1 的排列。
考虑对冲突分析:
由于数字是随机的,如果我们只有一位,那么冲突的概率约为 \dfrac{1}{2}。
由于 xor 操作对每一位是独立的,如果我们使用 k 位,则每次查询的冲突概率为 2^{-k}。
如果使用 64 位的随机整数(即 long long),那么每次查询冲突概率为 2^{-64},可以看成不会冲突。
例题二 (Loj 2788)
给出一个 n 个点 m 条边的无向图,不保证连通。将每个联通块视为子图,请求出每一个子图中的桥。你只有 16 MB 的内存空间。
#### 例题二 solution
这里我们只讨论图连通时的情况,不连通的话对每个连通块跑一遍就好。
首先这个数据范围明显就不想让我们把图全部存下来。
所以直接跑 Tarjan 是不行的。
现在让我们分析一下日常的 Tarjan 算法求桥到底是在干什么。
Tarjan 算法流程是,首先跑出一颗 DFS 生成树,然后注意到生成树上只有树边和返祖边。我们记录只通过返祖边所能返回的深度最浅的祖先是什么,然后如果一个儿子能通过返祖边返回的最浅的祖先比自己还深,那么这条边就一定是割边(桥)。
路人甲:……这好像不能优化啊?
作者:……谔谔确实。不过你的生成树不一定必须是 DFS 生成树啊!
考虑对原图任意建一颗生成树。不难发现割边只可能是生成树上的边。
观察一条非树边对答案贡献了什么。容易发现,一条非树边 $(u,v)$ 就是把树上从 $u$ 到 $v$ 的路径全部设为非割边。就像这样:
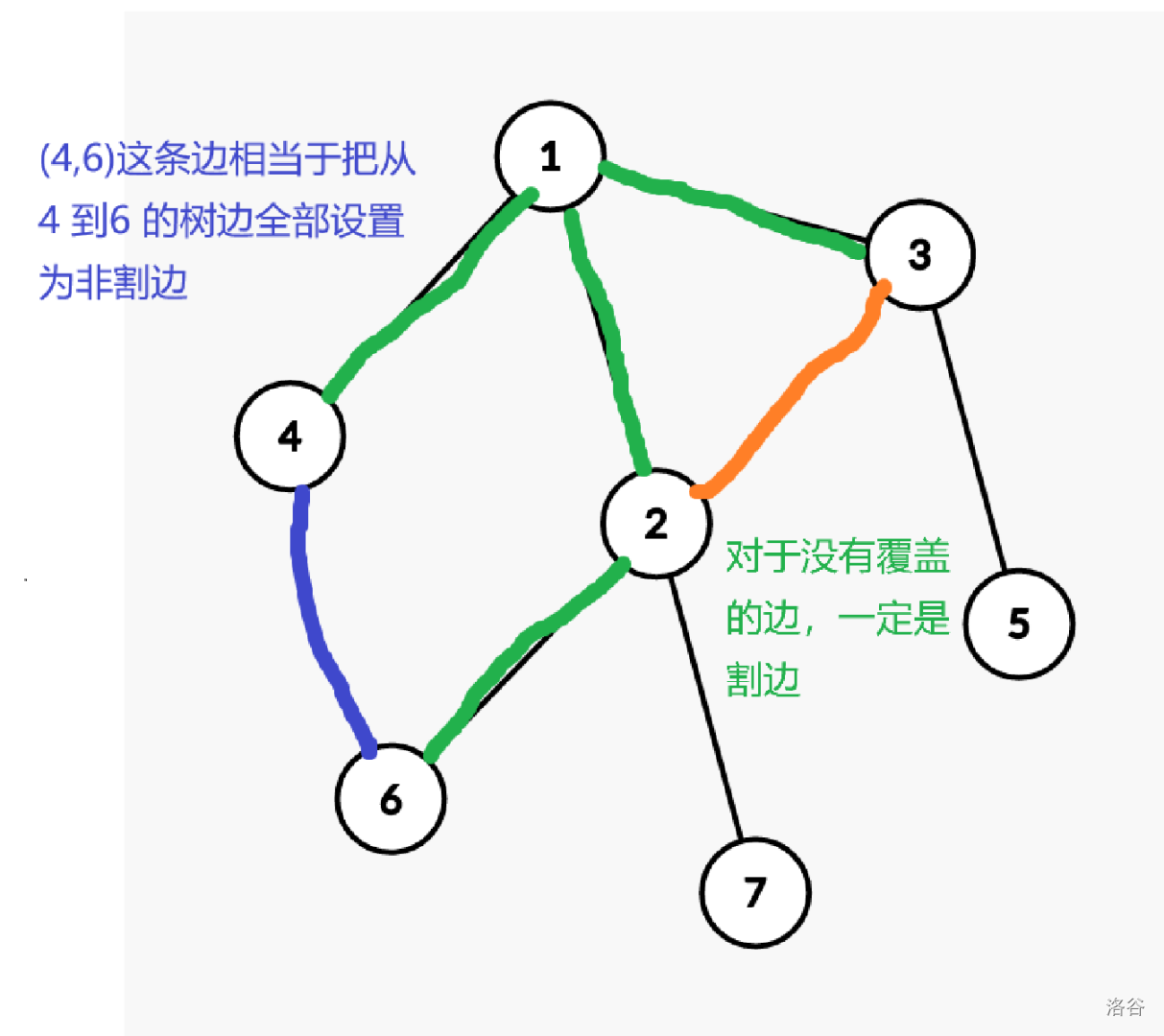
下面我们的问题就变成了如何快速覆盖一条树上的路径。
考虑 xor hashing:
对于每一条非树边,我们在这条非树边的两个端点的点权同时异或上一个随机值。
输入完成后我们 DFS 一遍这棵生成树,让节点的点权变成这棵子树内点权的异或和。如果 DFS 时发现儿子的点权是 0,那么这条边我们就认为是割边。
为什么呢?
注意到我们异或运算的第一个性质:$x\oplus x = 0$。这意味着如果一个数在区间内出现了 2 次(或者说偶数次),那么它对异或和的贡献一定为 $0$。那么对于一个子树,如果它的异或和等于 0,那么我们就可以认为每条边都出现了偶数次。
Code:
```cpp
#include<bits/stdc++.h>
using namespace std;
int n,m;
int fa[100010],d[100010];
vector<int>e[100010];
int find(int x){
if(x==fa[x])return x;
return fa[x]=find(fa[x]);
}
void dfs(int x,int pre){
for(auto i:e[x]){
if(i==pre)continue;
dfs(i,x);
if(!d[i])cout<<x<<" "<<i<<endl;
d[x]^=d[i];
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>m;
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
if(find(u)==find(v)){
int r=rand();
d[u]^=r,d[v]^=r;
}else{
fa[find(u)]=find(v);
e[u].push_back(v);
e[v].push_back(u);
}
}
for(int i=1;i<=n;i++){
if(find(i)==i)dfs(i,i);
}
return 0;
}
```
注:这道题 OI-Wiki 上还有一种解法,另外还有一种用 LCT 维护动态连通性的做法,不过都没有这个代码简洁。
### 练习
#### ABC250E Prefix Equality
##### 题面
给定两个长为 $N$ 的数列 $A,B$ 与 $Q$ 次询问,每次询问给出 $x_i,y_i$,求出 $A$ 的前 $x_i$ 项去重后是否与 $B$ 的前 $y_i$ 项去重后相同。
$1\leq n,q \leq 2\times 10^5, 1\leq a_i,b_i\leq 10^9$。
##### solution
异或哈希板子题。注意要离散化。
Code:
```cpp
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
mt19937_64 rng(2333);
int n,q;
int a[500050],b[500050],cnta[500050],cntb[500050];
int lsh[500050];
map<int,int>mp;
ll hsh[500050],prea[500050],preb[500050];
signed main(){
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)cin>>b[i];
int cnt=0;
for(int i=1;i<=n;i++){lsh[++cnt]=a[i];lsh[++cnt]=b[i];}
sort(lsh+1,lsh+cnt+1);
int unicnt=unique(lsh+1,lsh+cnt+1)-lsh-1;
for(int i=1;i<=unicnt;i++)mp[lsh[i]]=i;
for(int i=1;i<=n;i++){
a[i]=mp[a[i]];
b[i]=mp[b[i]];
}
for(int i=1;i<=unicnt;i++)hsh[i]=rng();
for(int i=1;i<=n;i++){
if(cnta[a[i]])prea[i]=prea[i-1];
else prea[i]=prea[i-1]^hsh[a[i]];
cnta[a[i]]++;
}
for(int i=1;i<=n;i++){
if(cntb[b[i]])preb[i]=preb[i-1];
else preb[i]=preb[i-1]^hsh[b[i]];
cntb[b[i]]++;
}
cin>>q;
while(q--){
int x,y;
cin>>x>>y;
if(prea[x]==preb[y])cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
return 0;
}
```
【注】:这题有 $\mathcal{O}(n)$ 的双指针做法。
#### CF1175F The Number of Subpermutations
上面的例一。$1 \leq n\leq 3\times 10^5$。
考虑枚举区间里的 1 , 分别往左右走到能走到的最大值就是区间的长度。使用前缀和优化一下即可。
Code:
```cpp
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int a[500050],n;
ll pre[500050],hse[500050],hs[500050];
mt19937_64 rng(19260817);
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)hs[i]=rng();
for(int i=1;i<=n;i++)hse[i]=hse[i-1]^hs[i];
ll ans=0;
for(int i=1;i<=n;i++)pre[i]=pre[i-1]^hs[a[i]];
for(int l=1,r=1;r<=n;r++){
if(a[r]==1){l=1,ans++;}
else{
l=max(l,a[r]);
if(r>=l&&(pre[r]^pre[r-l])==hse[l])ans++;
}
}
reverse(a+1,a+n+1);
for(int i=1;i<=n;i++)pre[i]=pre[i-1]^hs[a[i]];
for(int l=1,r=1;r<=n;r++){
if(a[r]==1){l=1;}
else{
l=max(l,a[r]);
if(r>=l&&(pre[r]^pre[r-l])==hse[l])ans++;
}
}
cout<<ans<<endl;
return 0;
}
```
【注】:这题存在确定性的 $\mathcal{O}(n)$ 和 $\mathcal{O}(n\log n)$ 做法。
#### CF1830C Hyperregular Bracket Strings
##### 题面
给定一个数 $n$ 和 $k$ 个区间 $\left[l_i,r_i\right]\in [1,n]$。
我们定义,对于一个长度为 $n$ 的,仅由 ```(``` 和 ```)``` 组成的合法括号序列,如果它的每一个区间 $\left[l_i,r_i\right]$ 内的子串都是合法括号序列,那么这个括号序列是**好的**。
求**好的**括号序列的数量,答案对 $998244353$ 取模。
##### solution
首先,括号序计数使用卡特兰数:长度为 $2n$ 的合法括号序列总共有 $\texttt{Cat}(n) = \frac{\binom{2n}{n}}{n+1}$ 种方案。
考虑如何处理区间相交、区间包含。
我们发现若区间相交,答案就是3个区间之积;若区间包含,答案就是去掉包含之后把两端拼在一起的方案数。
这一听就不好处理,这时候我们的异或哈希就要登场了!
考虑将一个区间 $[l,r]$ 必须是合法括号序列的限制视为将 $[l,r]$ 区间染色,如图:

然后我们惊奇的发现,我们可以把一段拥有相同颜色序列(你可以认为是颜色混合起来之后的同色)的一些区间拼在一起一块计数!
此时你就可以异或哈希(和例二一样),给每段区间一个随机的颜色,然后异或起来,得到答案。
细节看代码。
```cpp
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const ll mod = 998244353;
ll fac[800010],invfac[800010],inv[800010];
mt19937_64 rng(19240817);
ll qpow(ll a,ll b){
ll ans=1,base=a;
while(b){
if(b&1)ans=ans*base%mod;
base=base*base%mod;
b>>=1;
}
return ans;
}
int n,m;
struct node{
int l,r;
ll id;
}a[800050];
bool cmp(node x,node y){
if(x.l==y.l)return x.r<y.r;
return x.l<y.l;
}
void init(){
fac[0]=invfac[0]=1;
for(ll i=1;i<=800005;i++)
fac[i]=fac[i-1]*i%mod;
for(ll i=1;i<=800005;i++){
inv[i]=qpow(i,mod-2);
invfac[i]=qpow(fac[i],mod-2);
}
}
ll C(int n,int m){
if(n<m)return 0;
return fac[n]*invfac[m]%mod*invfac[n-m]%mod;
}
ll calc(int len){
if(len==0)return 1;
if(len&1)return 0;
len/=2;
return C(2*len,len)*inv[len+1]%mod;
}
ll b[800050];
map<ll,int>cnt;
void solve(){
cin>>n>>m;cnt.clear();
for(int i=1;i<=n;i++)b[i]=0;
for(int i=1;i<=m;i++){
cin>>a[i].l>>a[i].r;
a[i].id=rng();
b[a[i].l]^=a[i].id;
b[a[i].r+1]^=a[i].id;//类似差分的思想
}
ll t=rng();b[1]^=t,b[n+1]^=t;
for(int i=1;i<=n;i++){
b[i]^=b[i-1];
cnt[b[i]]++;
}
ll ans=1;
for(auto i:cnt){
if(i.second%2==1){//奇数不可能有合法括号序
cout<<0<<endl;
return;
}
ans=ans*calc(i.second)%mod;
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
int T;
init();
cin>>T;
while(T--)solve();
return 0;
}
```
【注】:本题存在确定性 $\mathcal{O}(n\log n)$ 做法(好多种)。
### 扩展——只能是二进制吗?
#### 例三 CF1418G
给你一个由 $n$ 个整数组成的数组 $a$ 。我们将子数组 $a[l..r]$ 命名为数组 $[a_l, a_{l + 1}, \dots, a_r]$ ($1 \le l \le r \le n$)。
如果子数组中出现的每一个整数都恰好出现三次,则该子数组被认为是好数组。例如,数组 $[1, 2, 2, 2, 1, 1, 2, 2, 2]$ 有三个良好的子数组:
- $a[1..6] = [1, 2, 2, 2, 1, 1]$ ;
- $a[2..4] = [2, 2, 2]$ ;
- $a[7..9] = [2, 2, 2]$ 。
计算给定数组 $a$ 的良好子数组数。
$ 1\leq n \leq 5\times 10^5$。
#### 例三 solution
考虑把问题转化为求同时满足以下两个条件的子数组数目:
- 子数组中的每一个值出现的次数都是3的倍数;
- 子数组中每个值出现的次数都小于等于三次。
考虑异或哈希。对于第一种情况,考虑拿一个桶记录一下每个数出现的次数对 3 取模,判断是否相等时只需看开始状态与最终状态在模三意义下是否完全一样即可。可以字符串哈希,不过异或哈希显然是更好的选择。
对于第二种情况,我们双指针维护即可。
Code:
```cpp
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
int n;
int a[500050];
mt19937_64 rng(2333);
int cnt[500050],tnc[500050];
ll xhs[500050],yhs[500050],pre[500050];
signed main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)xhs[i]=rng(),yhs[i]=rng();
for(int i=1;i<=n;i++){
cnt[a[i]]++;
if(cnt[a[i]]%3==2)pre[i]=xhs[a[i]];//[*]
if(cnt[a[i]]%3==1)pre[i]=yhs[a[i]];//[*]
if(cnt[a[i]]%3==0)pre[i]=xhs[a[i]]^yhs[a[i]];//[*]
pre[i]^=pre[i-1];
}
map<ll,ll>mp;
mp[0]=1;
ll ans=0;
for(int l=0,r=1;r<=n;r++){
tnc[a[r]]++;
while(tnc[a[r]]>3){
tnc[a[l]]--;
if(l)mp[pre[l-1]]--;
l++;
}
ans+=mp[pre[r]];
mp[pre[r]]++;
}
cout<<ans<<endl;
return 0;
}
```
【注】:这题存在确定性 $\mathcal{O}(n\log n)$ 做法以及另一种哈希方法。
#### 例三-扩展
如果不是 $3$,而是 $k$ 呢?
只需把上文标 `*` 的代码更改一下即可。
### 扩展——只能是异或吗?
分析我们刚刚干了什么。这些所有的例题里面,我们都有意或无意的利用了异或的 3 条性质:恒等律、归零律和交换律。这启发我们,能否使用另外一种满足交换律的运算,并且经过哈希操作之后在特定情况下哈希值会是一个特殊值呢?
我们想到了加法。加法同样具有以上说的三条性质:
$a+0=a,a+(-a)=0,a+b=b+a$。
所以我们可以用加法来实现哈希。
想想这是为什么。
考虑异或和加法的本质:
>异或的本质是对二进制每一位进行不进位加法
>
>加法的本质是对二进制每一位进行进位的加法
#### 例二 和哈希实现
用加法实现哈希的算法叫做“和哈希”(`sum hash`)。
算法的具体流程和异或哈希类似,不过在加入一段区间时,要在两边做不同的处理(如,`hash[l] += a,hash[r+1]-=a`),判断哈希值相等时要做减法。
Code:
```cpp
#include<bits/stdc++.h>
using namespace std;
int n,m;
int fa[100010],d[100010];
vector<int>e[100010];
int find(int x){
if(x==fa[x])return x;
return fa[x]=find(fa[x]);
}
void dfs(int x,int pre){
for(auto i:e[x]){
if(i==pre)continue;
dfs(i,x);
if(!d[i])cout<<x<<" "<<i<<endl;
d[x]+=d[i];
}
}
int main(){
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin>>n>>m;
for(int i=1;i<=n;i++)fa[i]=i;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
if(u>v)swap(u,v);
if(find(u)==find(v)){
int r=rand();
d[u]+=r,d[v]-=r;
}else{
fa[find(u)]=find(v);
e[u].push_back(v);
e[v].push_back(u);
}
}
for(int i=1;i<=n;i++){
if(find(i)==i)dfs(i,i);
}
return 0;
}
```
### 参考资料
[https://blog.csdn.net/notonlysuccess/article/details/130959107](https://blog.csdn.net/notonlysuccess/article/details/130959107)
[https://codeforces.com/blog/entry/85900](https://codeforces.com/blog/entry/85900)
[https://www.cnblogs.com/RuntimeErr/p/16797828.html](https://www.cnblogs.com/RuntimeErr/p/16797828.html)
[OI-Wiki](oi-wiki.org)
@Omphalos
@Ebola Ebola 好闪,拜谢 Ebola
orz。