DP的决策单调性优化总结

# 决策单调性的概念&证明工具: 决策单调性,是在**最优化**dp中的可能出现的一种性质,利用它我们可以降低转移的复杂度。 首先dp中会有转移,每个状态都由若干个状态转移而来,最优化dp比较特殊,只能由一个最优的状态转移而来。 我们称之为某个状态的最优转移点。 然后,dp会有一个转移顺序,比如说按层转移,从左到右转移等等(本质就是个DAG) 决策单调性,就是指状态的最优转移点随着dp顺序单调移动。 最经典的就是分段问题 : 将$[1,n]$分段,分出$(l,r]$需要$c(l,r)$的代价,问最小代价。 如果这个$c$函数啥性质都没有,显然是没有决策单调性的。怎么判定$c$函数是否具有决策单调性呢? 一种常用的方法是暴力`DP`观察转移点,这是篇讲理论的文章,这种方法就不多说了。 注意,下面讲的都是**最小化**问题,最大化请自行将权值部分的不等号反向。 - **四边形不等式** 假如我们有$p1\leq p2\leq p3\leq p4$. 则$c(p1,p3)+c(p2,p4)\leq c(p1,p4)+c(p2,p3)$称为四边形不等式。 简而言之,交叉$\leq$包含。 - $\boxed{\text{1D}}$ : 任意分 如果不限段数,分一段的代价为 $c(l,r)$,如果$c$满足四边形不等式,则该问题具有决策单调性。 设$F[i]$为把前$i$个位置分割完毕的最小代价。 $\color{blue}\text{证明:}$ 设$F[i]$的最优转移点为$p[i]$,我们假设有 $y<x$ 且 $p[x]<p[y]$。 根据最优决策的定义,写出相应的不等式: $$F[x]=F[p[x]]+c(p[x],x)\leq F[p[y]]+c(p[y],x)$$ 有$p[x]<p[y]<y<x$,由四边形不等式得 $$c(p[x],y)+c(p[y],x)\leq c(p[x],x)+c(p[y],y)$$ 同向不等式相加得到 $$F[p[x]]+c(p[x],y)\leq F[p[y]]+c(p[y],y)$$ 得到 $p[x]→y$ 比 $p[y]→y$ 更优,矛盾,故得证。 区间`DP`问题也是类似的。 - **包含单调** $p1\leq p2\leq p3\leq p4 \Rightarrow c(p1,p4)\geq c(p2,p3)$ 称之为包含单调。 - $\boxed{\text{2D}}$ : 分k段 在分k段问题中,有这样一个麻烦,如果分得短反倒亏,就可能不满足单调性。 如果$c$函数包含单调,那么分的段越多越好,就没这个问题了。(存疑) 应用可见 [stO 花神](https://www.luogu.com.cn/blog/pks-LOVING/solution-cf321e) ------------ # 常用优化手段: ### (1)有单峰性-单指针跳跃 - $\boxed{\text{1D}}$ “单峰性”的意思是:对于某个状态的最优转移点,其左边的贡献向左单调递减,右边也向右单调递减(一个单峰函数) 这个性质结合决策单调性,可以做到均摊$O(1)$转移,具体方法: 记录一个指针$p$表示转移点,由于决策单调性那么$p$不会往回跳。 进入了每一层之后,如果后面更优,$p$向后跳,否则停住并转移,根据单峰性这样子一定不会漏最优解。 那么$p$指针总共跳$O($状态$)$次,那么转移均摊$O(1)$. 例题:**暂无** ### (2)相邻层之间转移 - 分治 - $\boxed{\text{2D}}$ 这个适用于特殊的二维dp,只有上一层向下一层转移,同一层之间不会转移。 而且每一层中有决策单调性。 我们可以发现,一般暴力做是$O(n^2k)$(k是层数),每次转移需要多一个$O(n)$的$for$来枚举前一层。 又发现,在这一层,我们先转移哪一个位置是无关紧要的,因为同一层之间不会转移。 考虑分治,可以先转移$mid$,得到最优转移点是上一层的$p$。 之后,我们就能知道$[1,mid)$和$(mid,r]$分别对应候选转移点区间$[tl,p]$和$[p,tr]$(注意区间开闭). 这样子的分治复杂度是$O(nlogn)$的,不过好像并不显然。 证明的话,每一层的候选区间长度总和为$O(n)$,一共$O(logn)$层,总复杂度严格$O(nlogn)$ 例题:[P4072 [SDOI2016]征途](https://www.luogu.org/problem/P4072) (的$O(n^2logn)$辣鸡写法) ### (2+)贡献难算-分治&指针暴力跳 - $\boxed{\text{2D}}$ 这只能算是一个小技巧吧。 (先看)例题:[CF833B The Bakery](https://www.luogu.org/problem/CF833B) 这个决策单调性在这里不证明了,感性理解就是选的区间越长越可能亏。 (直接拿暴力dp打出决策点的表,然后大眼观察也可以) 请大家先想一下$O(n^3k)$的暴力。 这题难就难在无法$O(1)$或者$O(logn)$算出区间颜色数,我们的复杂度强行多了一个$n$. 先直接套用(2)的分治,区间颜色数是莫队的拿手好戏,我们考虑模仿莫队,维护两个指针跳来跳去。 然后一个很暴力的想法是,问到那个区间,就跳到哪个区间。 第一眼看上去复杂度似乎假了,但是分治树自有它的特殊性质: 对于$mid$的查询,我们会询问$\forall_{i=tl}^{mid}s(i,mid)$ 右端点是固定的,那么左端点一共只会移动$O($候选区间长度$)$次。 当处理$[l,r][tl,tr]$这一任务时,$l,r$指针一定属于$[tl,tr]$. 然后要向儿子分治求解,给到左儿子的时候要先暴力跳到$[tl,midL]$,同样不会跳出$[tl,tr]$ 从左儿子那里还回来之后,暴力给右儿子准备,不会跳出$[tl,tr]$。 这一部分也只会移动$O($候选区间长度$)$次。 根据(2)的证明,一次分治总复杂度就依然是$O(nlogn)$ **附:** [P5574 [CmdOI2019]任务分配问题](https://www.luogu.com.cn/problem/P5574) ### (3)二分队列 - $\boxed{\text{1D}}$ 方程形如$f[i]=\min\limits_{j=0}^{i-1}f[j]+w(i,j)$ 决策单调性的推论:有两个决策位置$i,j(i<j)$。 我们让$i,j$向$k$尝试着转移,不妨设$i$更优。 随着$k$的增大(右移),$j$有可能变得比$i$更优,但是此后$i$就永无翻身之日了。 也就是说,每个出发点能最优的目的地是一个区间,而且只会被后面的决策反超。(这和经典决策单调性是等价的) 这个过程暗示着一个分界线$k'$在这前面的$k$,用$i$转移更优,在这后面的用$j$转移更优。 如果我们能快速计算贡献函数 $w$ 的话,就能用$O(\log n)$的代价计算出两个决策位置$i,j(i<j)$的分界线$k'$。 换句通俗的话说,$j$能在到达$k'$之后怼掉$i$。 然后,我们按照优劣维护一个单调队列,那么队首就是目前的最优转移。 - **退役 : 弹出队首** 每一个候选点都想怼掉前面那个目前比他优的点,我们存下每个点能叉掉前一个点的位置。 如果$k$前进了,我们要判断队首有没有被下一个叉掉,如果有就弹出。 - **新人 : 队尾加入决策** 考虑一个候选决策点的命运,随着$k$的增大为时间线,无非是先养精蓄锐,然后叉掉别人,然后再被别人叉掉。 前面的决策随着$k$增大可能会被后面的反超,则是经典的决策单调性,由于要养精蓄锐,我们从队尾加入新决策。 假如这个决策能比最后一个更快地叉掉倒数第二个,则pop最后一个,一直进行…… 最后把新决策加入进去,这被称为二分队列。 观察可得这个队列是**同时**根据优劣和叉掉上一个人的时间为序的,这就可以保证所有叉人活动只在队首进行。 例题:[P1912 [NOI2009]诗人小G](https://www.luogu.org/problem/P1912) ### (3+)二分栈 - $\boxed{\text{1D}}$ 严格来讲这东西并不是所谓的决策单调性,但是和(3)十分类似,所以附带着讲讲。 还是最小化问题,方程:$f[i]=\min\limits_{j=0}^{i-1}f[j]+w(i,j)$ 每个出发点能最优的目的地是一个区间,但是 : 某种决策只会被**更前的**决策反超. 考虑某个决策的命运,随着$k$的增大为时间线,一开始就叉掉别人(注意这些人都是前面的,如果叉不掉就相当于被别人叉掉,根据上述性质就永无翻身之日了) 然后苟一会,再被别人(前面后面都有可能)叉掉。 (所以这个东西根本没有决策单调性啊) 看起来比较复杂,但是决策分界点仍然可以二分求出来,拿一个栈就能维护了。 还是套路,维护每个点能叉掉前一个点的位置,如果栈顶被叉掉了就弹出来。 由于只能在一开始怼人,加入元素的时候需要从栈顶加入,加入方法**不是**叉栈顶,而是比较优劣,如果劣于栈顶就直接丢掉,否则push进去。 然后,根据(3)的经验需要同时根据优劣和叉掉上一个人的时间为序。 我们在push前还要比较 : **栈次顶**会不会在能够叉掉新决策之前就被下一个干掉(其实就是维护分界点有序),如果是就弹出来。 这样子就被称为二分栈。 **例题** : [P3515 [POI2011]Lightning Conductor](https://www.luogu.org/problem/P3515) ### (4)斜率优化 - $\boxed{\text{1D}}$ 好像技能树点反,怎么先学了二分队列……不管了。 还是极化问题,方程 : $f[i]=\min\limits_{j=0}^{i-1}f[j]+w(i,j)$ 如果能把$w(i,j)$表示成$(i)'+(i)(j)+(j)'+C$的形式。 即两坨分别与$i,j$有关的常数和与两者都有关的**乘积**的和。(很多方程都满足这个要求) $(i)'+C$相对决策是固定不变的,不需要考虑。 我们把$(i)(j)+(j)'$看做一条直线,$(i)$的位置是$x$,决策$j$提供了斜率和截距。 我们所做的就是每次用一个$x$来切目前的所有直线(决策),来看看那个更优。 显而易见的是,我们需要维护一个上凸壳或者下凸壳(斜率有序)。 现在就变成了一个**数据结构维护凸壳**的问题。 由于凸壳的单调性,一般有两个重要性质能够加以利用 : **①插入斜率有序** , **②询问$x$点单增**。 - 同时满足①② 我们只需要单调队列(半平面交)维护凸壳,每次取队首即可。 具体的方法: - 队列里维护直线,以及与上一条直线的交点$x$坐标。 - 如果队首被第二个线超过了(看交点),弹出。 - 如果队尾超过倒数第二的时候,已经被新来的人超过了(看交点),弹出。 其实和二分队列本质上是一个东西,只不过不用二分了。 注意特判没有交点的情况,这时应该根据截距保留。 (一般不用考虑斜率不存在的情况) 例题 : [P3195 [HNOI2008]玩具装箱TOY](https://www.luogu.org/problem/P3195) $\qquad$[P4072 [SDOI2016]征途](https://www.luogu.org/problem/P4072) (**2D**) - 仅满足① 还是单调队列维护凸壳,询问在上面二分(直接看交点管理区间)即可。 - 啥都不满足 平衡树(`std::set`)硬上,查询`lower_bound`,写起来感觉毒瘤…… 也可以李超树,一般来讲写起来比较轻松。 还可以`CDQ`分治之类的。 # 广义决策单调性 维度更高,一些奥妙的东西。 - **路径交错** 考虑分k段问题,如果段数`+1`,形成的决策路径必然交错,如下图上半部。 如果出现了下半部的情况,则不合法。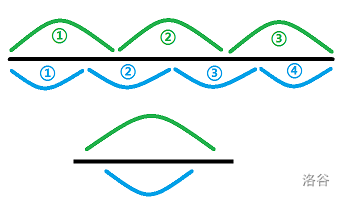  赛场上同样可以打表观察。 如果满足决策单调性,则必然满足路径交错,证明如下: 考虑蓝③的起始点,我们可以把蓝③的终点看做结束点,这比绿③靠前。 如果蓝③的起始点仍在绿③内,这会导致绿③的起始点甚至在蓝③前面,违背了决策单调性。 然后我们就又知道了蓝②的起点在绿②的前面。 通过反向归纳,我们能够得知 : 每个绿色的拱内,都最多只会有一个蓝点。 然后根据鸽笼原理不难得到每个绿拱内恰有一个蓝点。 这有一个好处,所有决策点的决策范围总和是$O(n)$的,所以我们暴力枚举范围就很优了。 **例题** : [CF321E Ciel and Gondolas](https://www.luogu.com.cn/problem/CF321E) 的$O(n^2)$做法。[stO 花神](https://www.luogu.com.cn/blog/pks-LOVING/solution-cf321e) [P4767 [IOI2000]邮局](https://www.luogu.com.cn/problem/P4767) 同样可以$O(n^2)$做掉。 - **环上路径交错** 仍然是分k段问题,这次整到环上来了。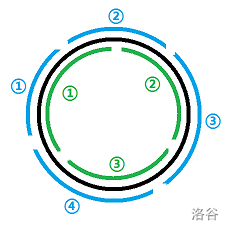 画成图大概是这样的 :  注意,此时蓝①被包在绿①内了,根据鸽笼原理这是必然出现的。 实际上也只会出现一个,证明考虑从①处断开,然后就变成序列问题,沿用结论即可。 另一种环上路径交错 : 钦定某个起点求出最优解,和钦定另一个起点的方案交错(段数相同)。 **例题** : 环状邮局 - $O(n^2klogn)$ 可以枚举某个决策点,然后大力拆环为链。 变成了$n$个经典分k段问题,大力按层单调性分治分治即可$O(nklogn)$。 - $O(n^2\log n)$ 考虑路径交错,先$O(nk\log n)$求出任意一种方案,然后剩余的所有方案就都是交错的。 选取最短的(决策点最少)一段,这一段的长度是$O(n/k)$的,在这一段里面枚举起点即可。 总复杂度是$O(n^2\log n)$. 接下来是$O(n\log S)$的魔法。 先考虑如何快速求出任意一种钦定起点的方案。 能够感知这是凸的,使用`WQS`二分+二分队列即可做到$O(n\log n\log S)$。 但是可能在构造方案上遇到一点麻烦……可以玄学扰动避免答案凸包三点共线。 当然还有比较系统的构造方法,改日研究。 得到了一种方案之后,我们进行决策单调性分治。由于路径交错,各个点的决策长度总和是$O(n)$的。 考虑把一段段的东西拆下来分层排成一排,则有这样的模式:  一条折线则表示某种钦定起始点的决策,不难发现折线相交就代表着路径不交错,所以所有折线都是不交的。 现在重头戏来了,我们对起始点分治,对于后面的点依次**枚举决策区间**进行转移,能够找到一条折线。 这条直线把所有的层分成了两部分,大小和为$O(n)$,于是分治下去找折线,复杂度是$O(n\log n)$的。