微积分学习笔记
Fido_Puppy
·
·
个人记录
\texttt{Preface}
主要是参照 \text{3 Blue 1 Brown} 的 【官方双语/合集】微积分的本质 - 系列合集 做的学习笔记。
微元思想
咕咕咕……
导数的概念
咕咕咕……
简单函数求导
假设我们要求 f(x) = x ^ 2 的导数。
我们可以假设一个很小的数 dx,然后写出下面这个式子:
\dfrac{f(x + dx) - f(x)}{dx}
将 f(x) = x ^ 2 代入得:
\dfrac{x ^ 2 + 2x \cdot dx + {dx} ^ 2 - x ^ 2}{dx} = 2x + dx
当 dx 越来越小的时候,dx 这项就可以被忽略了,于是只剩下了 2x。
\therefore \dfrac{d}{dx}(x ^ 2) = 2x
下面是一些简单函数的导数:
\text{Power Rule}
\dfrac{d}{dx}(x ^ n) = n x ^ {n - 1}
以及三角函数求导:
\dfrac{d}{dx}(\sin(x)) = \cos(x)
\dfrac{d}{dx}(\cos(x)) = -\sin(x)
复合函数求导
\text{Sum Rule}
两个函数的和的导数等于这两个函数的导数的和。
\dfrac{d}{dx}(f(x) + g(x)) = \dfrac{df}{dx} + \dfrac{dg}{dx}
这条定理比较简单,下面来证明一下:
\dfrac{d}{dx}(f(x) + g(x)) = \dfrac{df + dg}{dx} = \dfrac{df}{dx} + \dfrac{dg}{dx}
\text{Product Rule(乘积法则)}
\dfrac{d}{dx}(f(x) \cdot g(x)) = \dfrac{dg}{dx}\cdot f(x) + \dfrac{df}{dx}\cdot g(x)
这条定理还是比较好证明的:
\dfrac{d}{dx}(f(x) \cdot g(x)) = \dfrac{(f(x) + df)(g(x) + dg) - f(x) \cdot g(x)}{dx}
将上面的式子展开,就变成了:
\dfrac{df \cdot g(x) + dg \cdot f(x) + df \cdot dg}{dx} = \dfrac{dg}{dx}\cdot f(x) + \dfrac{df}{dx}\cdot g(x)
口诀可以被称作:左乘右导,右乘左导。
如果是一个常数乘一个函数的导数,结果就是这个函数的导数乘这个常数。
\dfrac{d}{dx}(\text{constant} \times f(x)) = \text{constant} \times \dfrac{df}{dx}
\text{Chain Rule(链式法则)}
\dfrac{d}{dx}f(g(x)) = \dfrac{df}{dg}(g(x)) \cdot \dfrac{dg}{dx}
举个栗子:
\dfrac{d}{dx}(\sin(x ^ 2)) = \cos(x ^ 2) \cdot 2x
指数函数求导
首先从 f(x) = 2 ^ x 入手,对其求导:
\dfrac{d}{dx}(2 ^ x) = \dfrac{2 ^ {x + dx} - 2 ^ x}{dx} = \dfrac{2 ^ {dx} \cdot 2 ^ x - 2 ^ x}{dx} = 2 ^ x \left( \dfrac{2 ^ {dx} - 1}{dx} \right)
容易发现最后面一项与前面的 x 无关:
\lim_{dx \to 0} \dfrac{2 ^ {dx} - 1}{dx}
把 dx = 0.00000001 代入,摁一下计算器,发现 \approx 0.69314718296221038455865012089399\cdots。
也就是说这是一个常数,\dfrac{df}{dx} 与 f(x) 是成比例的。
而有一个指数函数,它的导数就等于它本身,也就是说这个常数等于 1,这个函数就是 f(x) = e ^ x。
\lim_{dx \to 0} \dfrac{e ^ {dx} - 1}{dx} = 1, \dfrac{d}{dx}(e ^ x) = e ^ x
然后我们运用链式法则,将 f(x) = 2 ^ x 写成 f(x) = e ^ {\ln(2) \cdot x} 的形式:
\dfrac{d}{dx}(2 ^ x) = \dfrac{d}{dx}(e ^ {\ln(2) \cdot x}) = \ln(2) \cdot e ^ {\ln(2) \cdot x} = \ln(2) \cdot 2 ^ x
所以前面的那个常数也就是 \ln(2)。
一般我们将指数函数都写作 f(x) = e ^ {cx} 的形式,这样在幂上的常数 c 就显得一目了然了。
隐函数求导
类似 x ^ 2 + y ^ 2 = r ^ 2,这种不能够在严格意义上称作函数,只能表示变量之间关系的式子被称作隐函数。
举个栗子:
在平面直角坐标系中,以原点为圆心有一个半径为 5 的圆,求过圆上一点 (x, y) 的切线的斜率。
有一些数学基础就知道斜率 k = -{\left(\dfrac{y}{x}\right)}^{-1} = \dfrac{-x}{y},但是我们考虑如何用导数来解决这个问题。
x ^ 2 + y ^ 2 = 25
对于两边分别求导:
2x \cdot dx + 2y \cdot dy = 0
\therefore k = \dfrac{dy}{dx} = \dfrac{-x}{y}
再考虑如何求 f(x) = \ln(x) 的导数。
先把 f(x) = \ln(x) 看作一个隐函数:
y = \ln(x)
e ^ y = x
对于两边分别求导:
e ^ y \cdot dy = dx
\dfrac{dy}{dx} = \dfrac{1}{e ^ y} = \dfrac{1}{x}
极限
我们先从导数的正式定义中来理解极限的概念:
\text{Formal Definition of Derivatives}
\dfrac{df}{dx}(x) = \lim_{h \to 0} \dfrac{f(x + h) - f(x)}{h}
其中 \lim 表示极限的符号,底下的 h \to 0 表示当 h 逐渐逼近 0 时的取值。
\text{L'Hôpital's Rule(洛必达法则)}
当两个函数 f(x), g(x),其中当 x = a 时,f(x) = g(x) = 0,求:
\lim_{x \to a} \dfrac{f(x)}{g(x)}
正常的想法就是代入一个很接近 a 的数,但是这样只能求出一个近似值。
假设我们代入的是 a + dx,那么当两个函数图像无限放大之后,在 x = a 附近的部分可以近似看作两条直线,这样 f(a + dx) 可以被看作 \dfrac{df}{dx}(a),g(a + dx) 可以被看做 \dfrac{dg}{dx}(a)。
\therefore \lim_{x \to a} \dfrac{f(x)}{g(x)} = \dfrac{f'(x)}{g'(x)}
积分与微积分基本定理
我们来考虑有一个函数 v(t) 表示当时间为 t\ \text{seconds} 时汽车行驶的速度,考虑如何求出 s(t) 表示当时间为 t\ \text{seconds} 时汽车已经行驶的距离。
我们假设把时间轴分成很多个小段,每一段的时间都是 dt,并且每一小段内汽车都在做匀速直线运动,那么明显当 dt \to 0 时,这个近似值就越来越精确,最终我们会发现这个 s 就是 v 的函数图像与 x 轴围成的面积。
用积分来表示,就是:
s(t) = \int_{0}^t v(t)\cdot dt
我们考虑当 t 增加 dt 的时候,ds = v(t) \cdot dt,所以容易发现 s 的导数就是 v,这也就是积分运算。
举个栗子:
假设 v(t) = t(8 - t),求 s(t) 的表达式。
我们考虑什么函数的导数等于 t(8 - t),也就是 -t ^ 2 + 8t。
根据 \text{Power Rule} 和 \text{Sum Rule}:
s(t) = \int_0^t (-t ^ 2 + 8t)\cdot dt = -\dfrac{1}{3}t ^ 3 + 4t ^ 2
应用前缀和的思想,若要求 s(a, b) 表示从 a 到 b 时刻汽车行驶的距离,那么:
s(a, b) = \int_a^b v(t)\cdot dt = \left( \int_0^b v(t)\cdot dt\right) - \left(\int_0^a v(t)\cdot dt\right)
\text{Fundamental theorem of calculus(微积分基本定理)}
\text{if} \quad \dfrac{dF}{dx}(x) = f(x),
\text{then} \quad \int_a^b f(x)\cdot dx = F(b) - F(a).
若函数 $f(x)$ 有一段图像位于 $x$ 轴的下方,则其与 $x$ 轴围成的面积是负的,而积分计算的就是这种 $\text{“Signed area”(“有符号的面积”)}$。
## 微积分的应用
有一个函数 $f(x)$,如何求出在 $x \in [a, b]$ 范围内 $f(x)$ 的均值。
$$\text{Average} = \left( \int_a ^ b f(x) \cdot dx \right) \cdot {(b - a)} ^ {-1}$$
例如,求出 $f(x) = \sin(x)$ 在 $x \in [0, \pi]$ 内图像的平均高度。
$$\text{Average height} = \left( \int_0 ^ {\pi} \sin(x) \cdot dx \right) \cdot {\pi} ^ {-1}$$
$$ = (-\cos(\pi) + \cos(0)) \cdot {\pi} ^ {-1} = 2{\pi} ^ {-1}$$
## 高阶导数
在数值上,其实 $\dfrac{d ^ n f}{{dx} ^ n}$ 就相当于对于 $f(x)$ 求 $n$ 次导数后得到的结果。
举个物理中的栗子:
原函数 $s(t) \Leftrightarrow \text{Displacement(位移)}
一阶导数 \dfrac{ds}{dt}(t) \Leftrightarrow \text{Velocity(速度)}
二阶导数 \dfrac{d ^ 2 s}{{dt} ^ 2}(t) \Leftrightarrow \text{Acceleration(加速度)}
三阶导数 \dfrac{d ^ 3 s}{{dt} ^ 3}(t) \Leftrightarrow \text{Jerk(急动度)}
比如说一阶导数表示的是图像的斜率,二阶导数就表示了斜率的变化。
泰勒级数
举个栗子:
有时候我们需要求 $f(x) = \cos(x)$ 在某个点时 $f(x)$ 的值,但是三角函数却并不是那么好算,如果 $x$ 是在 $0$ 附近,那么我们就可以用 $f(x) = 1 - \dfrac{1}{2}x ^ 2$ 来近似的代替 $f(x) = \cos(x)$。
而这个 $f(x) = 1 - \dfrac{1}{2}x ^ 2$ 是怎么来的呢?这个就是一个泰勒多项式。
换个栗子:
我们要求一个多项式,使得它在 $x = 0$ 附近与 $f(x) = \sin(x)$ 的图像几乎贴合。
那么首先我们发现 $\sin(0) = 0$,所以我们这个多项式在 $x = 0$ 时一定也得时 $0$,那么常数项为 $0$。
接着我们希望在 $0$ 附近时,两个函数的斜率相等,因为 $\dfrac{d\sin(x)}{dx}(0) = \cos(0) = 1$,所以我们这个多项式就可以取 $f(x) = x$,这样它的导数在 $x = 0$ 时为 $1$。
然后我们有希望它们斜率的变化率,也就是凹凸程度也相等,那么因为 $\dfrac{d ^ 2 \sin(x)}{dx ^ 2} = -\sin(x) = 0$,所以我们这个多项式就可以取 $f(x) = x$,这样它的二阶导数在 $x = 0$ 时为 $0$。
以此类推,我们使得它们的三阶导数,四阶导数等都相等。
最后会发现一个无穷的多项式,当然这个就被我们称为**级数**了:
$$f(x) = x - \dfrac{1}{3!}x ^ 3 + \dfrac{1}{5!}x ^ 5 - \dfrac{1}{7!}x ^ 7 + \cdots$$
我们先算到 $\dfrac{1}{{13}!}x ^ {13}$,来看一下它和 $f(x) = \sin(x)$ 的图像:
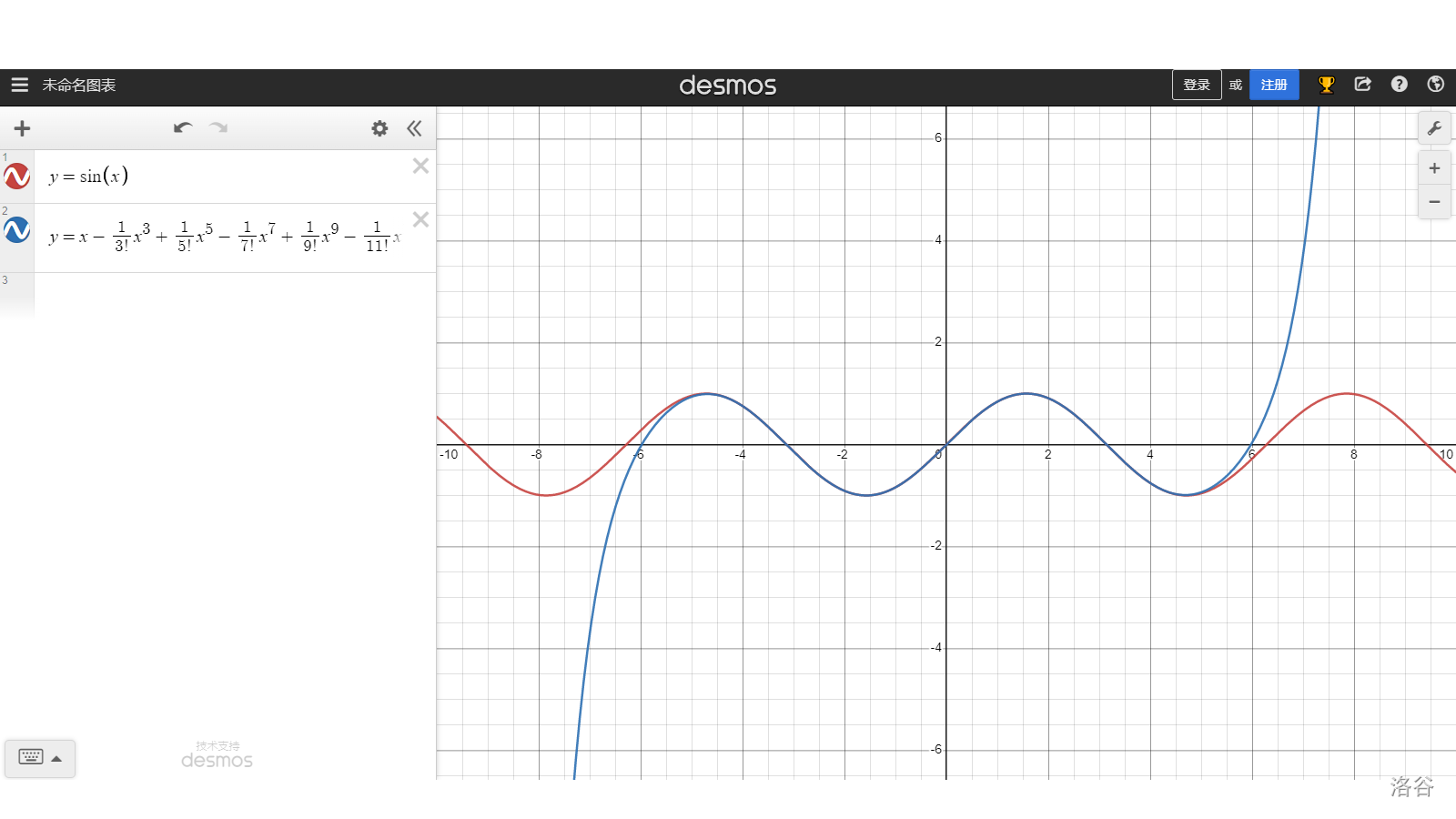
会发现在 $x = 0$ 附近已经十分贴合了。
我们还能够以同样的方式,来计算 $e$ 的近似值。
那么我们可以通过求出 $f(x) = e ^ x$ 的泰勒级数,然后代入 $x = 1$,就能求出 $e$ 的近似值了。
由于 $\dfrac{d ^ n e ^ x}{dx ^ n} = e ^ x$,当 $x = 1$ 时,$f(x) = e ^ x$ 的 $n$ 阶导数都是 $1$,所以可得:
$$f(x) = 1 + \dfrac{1}{1!}x + \dfrac{1}{2!}x ^ 2 + \dfrac{1}{3!}x ^ 3 + \dfrac{1}{4!}x ^ 4 + \cdots$$
那么 $e = 1 + \dfrac{1}{1!}+\dfrac{1}{2!}+\dfrac{1}{3!}+\dfrac{1}{4!}+\cdots$。
---
$$\texttt{Thanks for watching!}$$