矩阵树定理入土

[可能更好的 CSDN 阅读体验](https://blog.csdn.net/C20190102/article/details/107084966) 之前的一篇日报简单地介绍了矩阵树定理，重点可能放在 OI 题目上。本文将从数学角度完整并尽量通俗而详细地证明该定理，并附带一部分行列式的性质及证明。希望看完以后矩阵树将成为你信手拈来的一个 trick。 # 前置技能 - 简单的数学知识（函数、整除，并认识一些 OI 中常用的符号即可）。 - [高斯消元](https://blog.csdn.net/C20190102/article/details/103041769)（本质就是加减消元）。 # 行列式 ## 定义 对于一个 $n \times n$ 的矩阵 $A$，记它第 $i$ 行第 $j$ 列的元素为 $a_{i, j}$，以及一个 $1 \sim n$ 的排列 $p$，记 $$\lambda_A(p) = (-1) ^ {\tau(p)} \prod_{i = 1}^{n} a_{i, p_i}$$ （其中 $\tau(p)$ 是 $p$ 的逆序对个数）则 $$|A| = \det A = \sum_{p} \lambda_A(p) = \sum_{p} \left( (-1) ^ {\tau(p)} \prod_{i = 1}^{n} a_{i, p_i} \right)$$ （其中 $|A|$ 和 $\det A$ 都是 $A$ 的行列式的意思，后文有时为了便于区分行列式和绝对值会使用 $\det A$，其余大部分时候使用 $|A|$）显然行列式运算结果是数量。 简单理解一下发现这样的计算方法的时间复杂度是 $O(n \cdot \log n \cdot n!)$。~~因此这个定义没什么用~~ ## 性质 ### 拉普拉斯展开 对于一个 $n \times n$ 的矩阵 $A$ 和任意一个 $1 \leq i \leq n$，有 $$|A| = \sum_{j = 1}^{n} (-1)^{i + j} a_{i, j} |A_{i, j}|$$ 其中 $A_{i, j}$ 指矩阵 $A$ 删去第 $i$ 行和第 $j$ 列的所有元素后形成的一个 $(n - 1) \times (n - 1)$ 的矩阵。这个计算式称为对第 $i$ 行进行拉普拉斯展开。 > 证明： > 根据定义每个 $\lambda_A(p)$ 一定有一个因子 $x$ 满足 $x \in \{a_{i, 1}, a_{i, 2}, \cdots, a_{i, n}\}$，枚举 $j$ 得到这个因子 $a_{i, j}$ 和满足 $p_i = j$ 的排列 $p$，然后将这个 $p_i$ 删除，并把 $p$ 中所有大于 $j$ 的元素减一得到 $q$（$q$ 是 $1 \sim n-1$ 的排列），于是在 $n, i, j$ 确定时有了一个 $p$ 与 $q$ 之间的一一对应的函数关系。 > > 例如，当 $n = 3, i = 1, j = 2$ 时，满足 $p_1 = 2$ 的 $p$ 有 $\{2, 1, 3\}, \{2, 3, 1\}$，将 $2$ 删除，得到$\{1, 3\}, \{3, 1\}$，然后将 $3$ 减一，得到 $q$ 为 $\{1, 2\}$ 和 $\{2, 1\}$；根据 $n = 3, i = 1, j = 2$，亦可将 $q$ 还原为 $p$。 > > 令 $\xi(p) = q$，那么 > $$\left| \frac{\sum_{p} \lambda_A(p) \cdot [j = p_i]}{a_{i, j}} \right| = \left|\sum_{p} \lambda_{A_{i, j}}(\xi(p)) \cdot [j = p_i] \right|$$ > 右边变为直接枚举 $\xi(p)$，即 > $$\left| \frac{\sum_{p} \lambda_A(p) \cdot [j = p_i]}{a_{i, j}} \right| = \left|\sum_{q} \lambda_{A_{i, j}}(q) \right| = |\det A_{i, j}|$$ > $$\left| \sum_{p} \lambda_A(p) \cdot [j = p_i] \right| = |a_{i, j} \cdot \det A_{i, j}|$$ > 再考虑正负号，即 $\tau(p)$ 与 $\tau(\xi(p))$ 的奇偶性的差别，这取决于 $p_i$ 前面大于 $j$ 的数量和 $p_i$ 后面小于 $j$ 的数量，即 > $$\begin{aligned} & \sum_{k = 1}^{i - 1} [p_k > j] + \sum_{k = i + 1}^{n}[p_k < j] \\ =& \sum_{k = 1}^{i - 1} [p_k > j] + \left( j - 1 - \sum_{k = 1}^{i - 1}[p_k < j] \right) \\ =& \sum_{k = 1}^{i - 1} [p_k > j] + j - 1 - \left( i - 1 - \sum_{k = 1}^{i - 1}[p_k > j] \right) \\ =& 2\sum_{k = 1}^{i - 1} [p_k > j] + (i + j) \equiv i + j \mod 2\end{aligned}$$ > 于是 $\tau(p) = (-1)^{i + j} \tau(\xi(p))$，则 > $$\sum_{p} \lambda_A(p) \cdot [j = p_i] = (-1)^{i + j} \cdot a_{i, j} \cdot \det A_{i, j}$$ > 于是 > $$|A| = \sum_{p} \lambda_A(p) = \sum_{j = 1}^{n} \sum_{p} \lambda_A(p) \cdot [j = p_i] = \sum_{j = 1}^{n} (-1)^{i + j} a_{i, j} |A_{i, j}|$$ ### 线性性 #### 可乘性 对于任意 $1 \leq i \leq n$ 和 $k$，若 $A = \begin{pmatrix} a_{1, 1} & a_{1, 2} & \cdots & a_{1, n} \\ \vdots & \vdots & \ddots & \vdots \\ ka_{i, 1} & ka_{i, 2} & \cdots & ka_{i, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n, 1} & a_{n, 2} & \cdots & a_{n, n} \end{pmatrix}$，$B = \begin{pmatrix} a_{1, 1} & a_{1, 2} & \cdots & a_{1, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i, 1} & a_{i, 2} & \cdots & a_{i, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n, 1} & a_{n, 2} & \cdots & a_{n, n} \end{pmatrix}$，则 $|A| = k|B|$。 > 证明： > 根据定义，对于每个 $p$，$\lambda_A(p) = k \cdot \lambda_B(p)$，得证。 #### 可加性 对于任意 $1 \leq i \leq n$ 和 $k$， $$\begin{vmatrix} a_{1, 1} & a_{1, 2} & \cdots & a_{1, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i - 1, 1} & a_{i - 1, 2} & \cdots & a_{i - 1, n} \\ a_{i, 1} + b_{i, 1} & a_{i, 2} + b_{i, 2} & \cdots & a_{i, n} + b_{i, n} \\ a_{i + 1, 1} & a_{i + 1, 2} & \cdots & a_{i + 1, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n, 1} & a_{n, 2} & \cdots & a_{n, n} \end{vmatrix} = \begin{vmatrix} a_{1, 1} & a_{1, 2} & \cdots & a_{1, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i - 1, 1} & a_{i - 1, 2} & \cdots & a_{i - 1, n} \\ a_{i, 1} & a_{i, 2} & \cdots & a_{i, n} \\ a_{i + 1, 1} & a_{i + 1, 2} & \cdots & a_{i + 1, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n, 1} & a_{n, 2} & \cdots & a_{n, n} \end{vmatrix} + \begin{vmatrix} a_{1, 1} & a_{1, 2} & \cdots & a_{1, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i - 1, 1} & a_{i - 1, 2} & \cdots & a_{i - 1, n} \\ b_{i, 1} & b_{i, 2} & \cdots & b_{i, n} \\ a_{i + 1, 1} & a_{i + 1, 2} & \cdots & a_{i + 1, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n, 1} & a_{n, 2} & \cdots & a_{n, n} \end{vmatrix}$$ > 证明： > 对第 $i$ 行拉普拉斯展开即证。 ### 不重性 对于 $n \times n (n > 1)$ 的矩阵 $A$，若存在 $1 \leq i \leq n, 1 \leq j \leq n, j \neq j$ 使得对于任意 $1 \leq k \leq n$ 都有 $a_{i, k} = a_{j, k}$，即矩阵中某两行对应相等，则 $|A| = 0$。 > 证明： > 若某排列 $p$ 满足 $p_x = i, p_y = j (x < y)$，记 $q$ 为 $p$ 交换第 $x, y$ 个元素后得到的排列，即 $q_y = i, q_x = j (x < y)$，那么 $\lambda_A(p) = -\lambda_A(q)$，因为两者逆序对个数相差 $1$。 > 于是将所有 $1 \sim n$ 的排列这样两两配对，即可使所有 $\lambda_A(p)$ 抵消为 $0$，得证。 ### 可倍加性 对于任意 $1 \leq i \leq n, 1 \leq j \leq n, j \neq j$： $$\begin{vmatrix} a_{1, 1} & a_{1, 2} & \cdots & a_{1, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i, 1} & a_{i, 2} & \cdots & a_{i, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n, 1} & a_{n, 2} & \cdots & a_{n, n} \end{vmatrix} = \begin{vmatrix} a_{1, 1} & a_{1, 2} & \cdots & a_{1, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i, 1} + ka_{j, 1} & a_{i, 2} + ka_{j, 2} & \cdots & a_{i, n} + ka_{j, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n, 1} & a_{n, 2} & \cdots & a_{n, n} \end{vmatrix}$$ > 证明： > $$\begin{aligned} & \begin{vmatrix} a_{1, 1} & a_{1, 2} & \cdots & a_{1, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i, 1} + ka_{j, 1} & a_{i, 2} + ka_{j, 2} & \cdots & a_{i, n} + ka_{j, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n, 1} & a_{n, 2} & \cdots & a_{n, n} \end{vmatrix} \\ =& \begin{vmatrix} a_{1, 1} & a_{1, 2} & \cdots & a_{1, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i, 1} & a_{i, 2} & \cdots & a_{i, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n, 1} & a_{n, 2} & \cdots & a_{n, n} \end{vmatrix} + \begin{vmatrix} a_{1, 1} & a_{1, 2} & \cdots & a_{1, n} \\ \vdots & \vdots & \ddots & \vdots \\ ka_{j, 1} & ka_{j, 2} & \cdots & ka_{j, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n, 1} & a_{n, 2} & \cdots & a_{n, n} \end{vmatrix} & (\text{可加性}) \\ =& \begin{vmatrix} a_{1, 1} & a_{1, 2} & \cdots & a_{1, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i, 1} & a_{i, 2} & \cdots & a_{i, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n, 1} & a_{n, 2} & \cdots & a_{n, n} \end{vmatrix} + k\begin{vmatrix} a_{1, 1} & a_{1, 2} & \cdots & a_{1, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{j, 1} & a_{j, 2} & \cdots & a_{j, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n, 1} & a_{n, 2} & \cdots & a_{n, n} \end{vmatrix} & (\text{线性性}) \\ =& \begin{vmatrix} a_{1, 1} & a_{1, 2} & \cdots & a_{1, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i, 1} & a_{i, 2} & \cdots & a_{i, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n, 1} & a_{n, 2} & \cdots & a_{n, n} \end{vmatrix} + 0 & (\text{不重性}) \\ =& \begin{vmatrix} a_{1, 1} & a_{1, 2} & \cdots & a_{1, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{i, 1} & a_{i, 2} & \cdots & a_{i, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n, 1} & a_{n, 2} & \cdots & a_{n, n} \end{vmatrix} \end{aligned}$$ ### 转置不变性 任意一个 $n \times n$ 的矩阵 $A$，满足 $|A^T| = |A|$。$A^T$ 表示矩阵 $A$ 的转置，即 $a_{i, j} \to a_{j, i}$（换句话说，将 $A$ 沿“左上 - 右下”对角线翻折即得到 $A^T$），下同。 > 证明： > 对于一个排列 $p$，根据转置的定义，令 $\xi(p) = q\ (q_{p_i} = i)$，那么 $\lambda_A(p) = \lambda_{A^T}(\xi(p))$。考虑 $\tau(p)$ 和 $\tau(\xi(p))$ 的关系： > 把 $A_{i, p_i}\ (1 \leq i \leq n)$ 记做特殊点，令 $\mathcal{T}_p(i)$ 表示 $A_{i, p_i}$ 的左下方的特殊点数量， $\mathcal{T}'_p(i)$ 表示 $A_{i, p_i}$ 的右上方的特殊点数量，则 $\tau(p) = \sum_{i = 1}^{n} \mathcal{T}_p(i) = \sum_{i = 1}^{n} \mathcal{T}'_p(i)$，由于是沿对角线翻折，所以显然 $\mathcal{T}_p(i) = \mathcal{T}'_q(i)$（事实上只是把“左下方”的特殊点变到“右上方”，“右上方”变到“左下方”），于是 $\tau(p) = \tau(q)$。 > 因此 $\lambda_A(p) = \lambda_{A^T}(\xi(p))$，得证。 ### 可交换性 #### 行可交换性 矩阵两行交换，矩阵的行列式值反号。 > 证明： > 交换 $A$ 的两行 $u, v$ 可视为将 $v$ 行加到 $u$ 行上（①）得到一个新矩阵 $A'$，再从 $A'$ 的 $v$ 行上减去 $A'$ 的 $u$ 行（②），再将 $A'$ 的 $u$ 行全部取反（③）。根据可倍加性，① 和 ② 均不改变行列式的值，根据可乘性，③ 操作使行列式的值反号，得证。 #### 列可交换性 矩阵两列交换，矩阵行列式值反号。 > 证明： > 根据转置不变性，先转置再用行可交换性交换两行，再转置回来即证。 ## 优化行列式的计算 对矩阵 $A$ 的第一行进行拉普拉斯展开可以证明：当 $A$ 为一个上三角矩阵（即任意 $i > j$，满足 $a_{i, j} = 0$）时： $$|A| = \prod_{i = 1}^{n} a_{i, i}$$ 发现高斯消元用到的是可倍加性、可交换性，于是我们对 $A$ 高斯消元，可以得到一个上三角矩阵，这个矩阵的对角线乘积即为 $A$ 的行列式的绝对值（可交换性会使其反号）！于是我们做到了 $O(n^3)$ 求行列式的值。 # 矩阵树定理 ## 前置定义 对于一个无向图 $G = (V, E)$，其中 $|V| = n$（点数），$|E| = m$（边数）： - 给 $G$ 的每条边任意分配一个方向，则它的关联矩阵（大小为 $m \times n$） $B$： $$b_{i, j} = \begin{cases} 1 & \text{点}\ j\ \text{是边}\ i\ \text{的起点} \\ -1 & \text{点}\ j\ \text{是边}\ i\ \text{的终点} \\ 0 & \text{其他}\end{cases}$$ - $G$ 的基尔霍夫矩阵（大小为 $n \times n$）$L$： $$l_{i, j} = \begin{cases} d_i & i = j \\ -e_{i, j} & i \neq j\end{cases}$$ （其中 $d_i$ 表示 $i$ 号点的度，$e_{i, j}$ 连接点 $i, j$ 的边的数量） ## 一些引理 ### 转置引理 $$L = BB^T$$ $L, B, B^T$ 定义如上，乘法是矩阵乘法。 > 证明： > 按照矩阵乘法的规则展开即证。 > 事实上如果定义两个序列相乘的结果是对应位置的乘积之和的话，矩阵乘法将 $B$ 的列两两相乘得到了一个新矩阵，这个矩阵就是 $L$。 ### 连通性引理 #### 引理 1 若 $G$ 是一个连通图，那么 $|L| = 0$。 > 证明： > 若 $G$ 是连通图，那么根据定义 $L$ 的每一列的元素之和都为 $0$，再根据可倍加性，将其他所有行加到某一行上，这一行的元素就全部为零，再对这一行进行拉普拉斯展开，得到 $|L| = 0$。 #### 引理 2 若 $G$ 不连通，则对任意 $1 \leq i \leq n$，$|L_{i, i}| = 0$。 > 证明： > 根据行列可交换性，我们将同一联通块的点换到一起，得到的新矩阵 $L'$ 满足 $|\det L'| = |\det L|$，并且 $L'$ 长这个样子： > $$\begin{pmatrix} A_1 & \bold{0} & \bold{0} & \cdots & \bold{0} \\ \bold{0} & A_2 & \bold{0} & \cdots & \bold{0} \\ \bold{0} & \bold{0} & A_3 & \cdots & \bold{0} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \bold{0} & \bold{0} & \bold{0} & \cdots & A_k\end{pmatrix}$$ > （$\bold{0}$ 代表零矩阵，$k$ 是联通块的个数） > 由于 $G$ 不连通，所以 $k \geq 2$，所以 $L_{i, i}$ 至少包含一个 $A_x (1 \leq x \leq k)$。因为 $A_x$ 是一个独立连通子图，所以 $A_x$ 可以经过适当操作使得其对角线上某个元素为 $0$，进而 $|L_{i, i}| = 0$。 #### 引理 3 若 $G$ 是一个树，则对任意 $1 \leq i \leq n$，$|\det L_{i, i}| = 1$。 > 证明： > 将这个树的结点拓扑排序，使得对于任意点 $i$，去除掉所有 $1 \sim i - 1$ 的点后 $i$ 的度数为 $1$，这可以通过不断“摘掉”叶子结点实现。然后以这个顺序整理矩阵 $L$ 的各行得到 $L'$，我们对 $L'$ 模拟高斯消元的过程： > 假设当前到了第 $i$ 行。没有消元时，由于我们拓扑排序了，那么 $l'_{i, i}$ 右边（“右边”指所有 $l'_{i, j}\ (j > i)$，“左边”“上面”“下面”同理）和下面有且仅有 $1$ 个 $-1$，左边和上面有且仅有 $l'_{i, i} - 1$ 个 $-1$；由于我们用前 $i - 1$ 行消掉了 $l'_{i, i}$ 前面的 $l'_{i, i} - 1$ 个 $-1$， 并且 $l'_{i, i}$ 上面有 $l'_{i, i} - 1$ 个 $-1$，于是 $l'_{i, i}$ 被加了 $l'_{i, i} - 1$ 个 $-1$，就变成了 $1$。 > 按这样高斯消元下去，最后一个元素（$l'_{n, n}$） 肯定是 $0$。但我们要求的是 $|L_{i, i}| = |L'_{i, i}|$，它是 $L'$ 删去了一行一列，因此 $L'_{i, i}$ 消元过后的最后一个（$l''_{n - 1, n - 1}$）是 $1$。于是对角线上的元素全部是 $1$，得证。 ### Binet - Cauchy 定理 设 $A$ 是一个 $n \times m$ 的矩阵，$B$ 是一个 $m \times n$ 的矩阵，有 $$|AB| = \begin{cases} 0 & n > m \\ |A| \cdot |B| & n = m\\ \sum\limits_{1 \leq k_1 < k_2 < \cdots < k_n \leq m} |A(1, 2, \cdots, n; k_1, k_2, \cdots, k_n)| \cdot |B(k_1, k_2, \cdots, k_n; 1, 2, \cdots, n)| & n < m \end{cases}$$ （$A(1, 2, \cdots, n; k_1, k_2, \cdots, k_n)$ 表示由 $A$ 的第 $k_1, k_2, \cdots, k_n$ 列组成的矩阵；$B(k_1, k_2, \cdots, k_n; 1, 2, \cdots, n)$ 表示由 $B$ 的第 $k_1, k_2, \cdots, k_n$ 行组成的矩阵） > 证明： > 我们构造两个辅助矩阵： > $$M = \begin{pmatrix} A & \bold{0} \\ -I & B\end{pmatrix},\ \ N = \begin{pmatrix} \bold{0} & AB \\ -I & B\end{pmatrix}$$ > 其中 $I$ 是单位矩阵（“左上 - 右下”对角线为 $1$ 的矩阵）可以发现 $|M| = |N|$，证明如下： > 枚举 $M$ 矩阵的第 $i\ (n + 1 \leq i \leq n + m)$ 行，然后将第 $i$ 行乘以 $a_{k_1}$ 后加到第 $1$ 行，乘以 $a_{k_2}$ 后加到第 $2$ 行，……，乘以 $a_{k_n}$ 后加到第 $n$ 行。这样操作完后，根据矩阵乘法的定义，$M$ 变为了 $N$，又因为倍加不变性，$|M| = |N|$。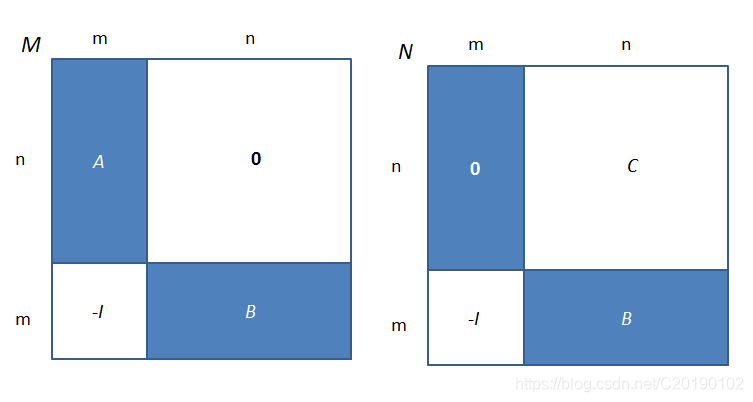 > 用定义式计算 $|N|$，由于只要 $p$ 选到 $\bold{0}$ 中的元素 $\lambda_N(p)$ 就为 $0$，所以只考虑 $p_1, p_2, \cdots, p_n \in [m + 1, m + n]$ 的情况，又因为 $AB$ 是个 $n \times n$ 的矩阵，所以 $p_{n + 1}, p_{n + 2}, \cdots, p_{n + m} \in [1, m]$，所以 > $$|N| = |AB| \cdot |-I| = (-1)^m |AB|$$ > > 接下来分类计算 $|M|$，并证明该定理： > > - 当 $n > m$ 时（图中 $C = AB$，下同）： >  > > 用定义式计算 $M$，发现排列 $p$ 无论如何取都会取到 $\bold{0}$ 中的元素（原因就是 $n > m$），因此 $|M| = 0$，即 $(-1)^m |AB| = 0$，即 $|AB| = 0$。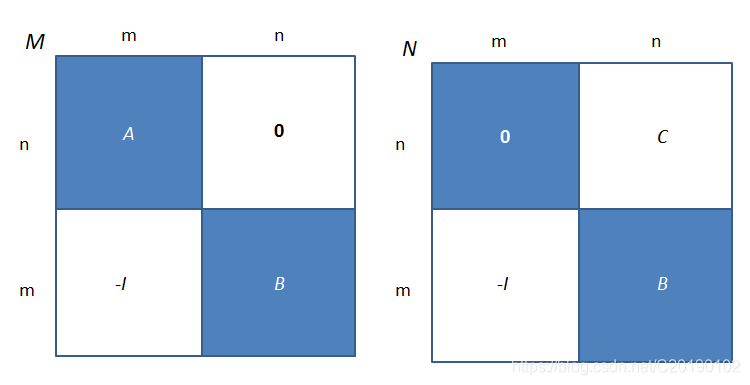 > - 当 $n = m$ 时： >  > > 用定义式计算 $M$，显然只有 $p_1, p_2, \cdots, p_n \in [1, n]$ 且 $p_{n + 1}, p_{n + 2}, \cdots, p_{n + m} \in [n + 1, n + m]$ 时 $\lambda_M(p)$ 不为 $0$，于是 > $$|M| = |A| \cdot |B| \cdot (-1)^{n^2}$$ > 其中 $(-1)^{n^2}$ 即为分开计算 $A, B$ 将两者的排列合起来新形成的逆序对数。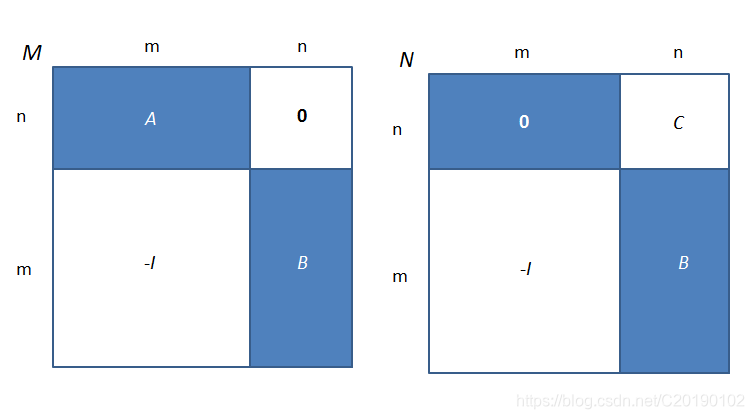因而 $|A| \cdot |B| \cdot (-1)^{n^2} = |AB| \cdot (-1)^m$，于是 > $$|A||B| = |AB|(-1)^{m - n^2} = |AB|(-1)^{n - n^2} = |AB|$$ > - 当 $n < m$ 时： >  > > 这时候我们枚举 $k_1, k_2, \cdots, k_n \in [1, m]$（就是定理中的 $k_1, k_2, \cdots, k_n$）表示在 $A$ 的各行中选的元素。为了使 $\lambda_M(p) \neq 0$，$-I$ 中就只能选对角线上的元素，又因为 $A$ 中选的元素的正下方的那个 $-1$ 肯定不能选（因为$p$ 是排列），所以在 $B$ 被选了元素的行一定和 $A$ 被选了元素的列一样。举个例子，假设 $n = 3$，红色是 $A\ /\ B$ 中含有被选中元素的列 $/$ 行。 >  > > 这样一来 $|A(1, 2, \cdots, n;k_1, k_2, \cdots, k_n)|$ 的那些排列就和 $|B(k_1, k_2, \cdots, k_n; 1, 2, \cdots, n)|$ 的那些排列形成了一一对应的函数关系，于是 > $$|M| = \sum\limits_{1 \leq k_1 < k_2 < \cdots < k_n \leq m} |A(1, 2, \cdots, n; k_1, k_2, \cdots, k_n)| \cdot |B(k_1, k_2, \cdots, k_n; 1, 2, \cdots, n)| \cdot (-1)^{m - n + x}$$ > 其中 $(-1)^{m - n}$ 是 $-I$ 的贡献， $x$ 是“新构成”的逆序对个数，所谓新构成，就是三部分的逆序对个数之和：$-I$ 与 $A$、$-I$ 与 $B$、$A$ 与 $B$。由于枚举出的东西关于对角线对称，所以$-I$ 与 $A$ 之间的逆序对数等于 $-I$ 与 $B$ 之间的逆序对数，于是 $x$ 可以转化为 $A$ 与 $B$ 之间的逆序对数，即 $n^2$。于是 > $$\begin{aligned} |M| &= \sum\limits_{1 \leq k_1 < k_2 < \cdots < k_n \leq m} |A(1, 2, \cdots, n; k_1, k_2, \cdots, k_n)| \cdot |B(k_1, k_2, \cdots, k_n; 1, 2, \cdots, n)| \cdot (-1)^{m - n + x} \\ &= \sum\limits_{1 \leq k_1 < k_2 < \cdots < k_n \leq m} |A(1, 2, \cdots, n; k_1, k_2, \cdots, k_n)| \cdot |B(k_1, k_2, \cdots, k_n; 1, 2, \cdots, n)| \cdot (-1)^{m - n + n^2} \\ &= |AB| (-1)^m \end{aligned}$$ > 于是 > $$\begin{aligned} |AB| &= \sum\limits_{1 \leq k_1 < k_2 < \cdots < k_n \leq m} |A(1, 2, \cdots, n; k_1, k_2, \cdots, k_n)| \cdot |B(k_1, k_2, \cdots, k_n; 1, 2, \cdots, n)| \cdot (-1)^{n^2 - n} \\ &= \sum\limits_{1 \leq k_1 < k_2 < \cdots < k_n \leq m} |A(1, 2, \cdots, n; k_1, k_2, \cdots, k_n)| \cdot |B(k_1, k_2, \cdots, k_n; 1, 2, \cdots, n)| \end{aligned}$$ > 定理得证。 该证明参考了 Freopen 大佬的博客，详见参考资料。~~同样百度百科上有个很线代的证明。~~ ## 矩阵树定理 对于 $n$ 个点 $m$ 条边的无向图 $G$ 以及任意一个 $1 \leq i \leq n$，$|L_{ii}|$ 即为它的生成树个数。 > 证明： > 由转置引理 > $$|L_{i, i}| = |B_{i, i} B_{i, i}^T|$$ > 因为 $B_{i, i}, B_{i, i}^T$ 分别是大小为 $(n - 1) \times (m - 1), (m - 1) \times (n - 1)$ 的矩阵，所以由 Binet - Cauchy 定理得 > $$|L_{i, i}| = |B_{i, i} B_{i, i}^T| = \sum_{1 \leq k_1 < k_2 < \cdots < k_{n - 1} \leq m} |B_{i, i}(1, 2, \cdots, n - 1; k_1, k_2, \cdots, k_{n - 1})| \cdot |B_{i, i}^T(k_1, k_2, \cdots, k_{n - 1}; 1, 2, \cdots, n - 1)|$$ > 由于 $B_{i, i}(1, 2, \cdots, n - 1; k_1, k_2, \cdots, k_{n - 1}) = B_{i, i}^T(k_1, k_2, \cdots, k_{n - 1}; 1, 2, \cdots, n - 1)$，所以 > $$\begin{aligned} |L_{i, i}| = |B_{i, i} B_{i, i}^T| &= \sum_{1 \leq k_1 < k_2 < \cdots < k_{n - 1} \leq m} |B_{i, i}(1, 2, \cdots, n - 1; k_1, k_2, \cdots, k_{n - 1})| \cdot |B_{i, i}^T(k_1, k_2, \cdots, k_{n - 1}; 1, 2, \cdots, n - 1)| \\ &= \sum_{1 \leq k_1 < k_2 < \cdots < k_{n - 1} \leq m} |B_{i, i}(1, 2, \cdots, n - 1; k_1, k_2, \cdots, k_{n - 1})|^2 \end{aligned}$$ > 由关联矩阵的定义可知，$B' = B_{i, i}(1, 2, \cdots, n - 1; k_1, k_2, \cdots, k_{n - 1})$ 就是由图 $G$ 的边 $k_1, k_2, \cdots, k_{n - 1}$ 构成的子图 $G'$ 的关联矩阵。由连通性引理二得，当 $G'$ 不连通时，$|B'| = 0$；由连通性引理三得，当 $G'$ 是树时，$|\det B'| = 1$，因此 $|B_{i, i}(1, 2, \cdots, n - 1; k_1, k_2, \cdots, k_{n - 1})|^2 = 1$ 当且仅当由图 $G$ 的边 $k_1, k_2, \cdots, k_{n - 1}$ 构成的子图是树，得证。 # 参考资料 [**Matrix - Tree 定理（生成树计数）的另类证明和简单拓展** - MoebiusMeow](https://www.cnblogs.com/meowww/p/6485422.html) [**矩阵树定理** - Freopen](https://blog.csdn.net/qq_35950004/article/details/88074268) [**Matrix - Tree 矩阵树定理** - Lucky_Glass](https://4rds5h.coding-pages.com/2020/20Jun28thArt1/) [**拉普拉斯展开** - 百度百科](https://baike.baidu.com/item/%E6%8B%89%E6%99%AE%E6%8B%89%E6%96%AF%E5%B1%95%E5%BC%80) [**Binet - Cauchy 定理** - 百度百科](https://baike.baidu.com/item/Binet-Cauchy%E5%AE%9A%E7%90%86)