不定积分&积分法

· · 个人记录

中值定理&泰勒展开&洛必达法则&函数凹凸及绘制

不定积分

通俗来讲就是导数的逆运算，要将导函数还原成原函数。

由于在“导”的时候，我们做了一些“取舍”，所以会导致找到的原函数不唯一。

例子：

(x^3)^{'}=3x^2,(x^3+2)^{'}=3x^2 c$ 为常数：$(x^3+c)^{'}=3x^2

如果 F^{'}{(x)}=f{(x)}，那么 F{(x)} 是 f(x) 的一个原函数。

定义：

f(x)

原函数全体。

\int{f(x)dx} - 练习（请保证导数各种公式已经非常熟悉）： - $1$： $$\int{x^2dx}=\frac{1}{3}x^3+c$$ $$(x^3)^{'}=3x^2\Rightarrow x^2=(\frac{1}{3}x^3)^{'}$$ $$(x^n)^{'}=nx^{n-1}$$ 注意 $c$ 一定不能省略，它代表一个常数，我们表达的是原函数**全体**。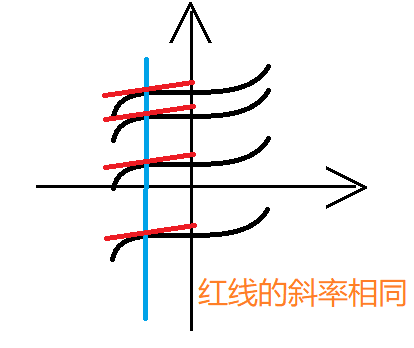 $$\int{x^ndx}=\frac{1}{n+1}x^{n+1}+c$$ - $2$： $$\int{\frac{1}{\sqrt{1-x^2}}dx}=\arcsin x+c$$ $$(\arcsin x)^{'}=\frac{1}{\sqrt{1-x^2}}$$ - $3$（定义域不同）： $$\int{\frac{1}{x}dx}= \begin{cases} \ln x+c (x > 0)\\ \ln (-x)+c(x<0) \end{cases} =\ln|x|+c $$ $$(\ln x)^{'}=\frac{1}{x}$$ - 几何意义：（$c$ 的不同使函数图像上下移动，上加下减） ![斜率相同](https://s4.ax1x.com/2021/12/14/ojMXo8.png) - $4$： $(2,5)$ 的切线斜率为 $2x$： $$\int{2xdx}=x^2+c$$ $$y=x^2+c$$ $$5=4+c$$ $$c=1$$ $$y=x^2+1$$ 性质： - $1$： $$(\int{f(x)dx})^{'}=f(x)$$ - $2$： $$\int{f^{'}{(x)}dx}=f(x)+c$$ 当有常量或和 $x$ 的无关变量可以直接外提（假设 $k$ 是与 $x$ 无关变量）： $$\int{kf(x)dx}=k\int{f(x)dx}$$ $$\int{3f(x)dx}=3\int{f(x)dx}$$ - $3$： $$\int{(f_1(x)+f_2(x)+…+f_n{(x)})dx}=\int f_1{(x)}dx+\int f_2{(x)}dx+…+\int f_n{(x)}dx$$ ### 基本积分公式 - $1$： $$\int{0dx}=c$$ （$c$ 是常数） - $2$： $$\int{x^adx}=\frac{1}{a+1}x^{a+1}+c$$ $$(a\not=-1)$$ - $3$： $$\int{\frac{1}{x}dx}=\ln|x|+c$$ - $4$： $$\int{a^xdx}=\frac{1}{\ln a}a^x+c$$ - $5$： $$\int{e^xdx}=e^x+c$$ - $6$： $$\int{\sin xdx}=-\cos x+c$$ - $7$： $$\int{\cos xdx}=\sin x+c$$ - $8$： $$\int{\sec^2 xdx}=\tan x+c$$ - $9$： $$\int{\csc^2 xdx}=-\cot x+c$$ - $10$： $$\int{\frac{1}{\sqrt{1-x^2}} dx}=\arcsin x+c$$ - $11$： $$\int{\frac{1}{1+x^2} dx}=\arctan x+c$$ - $12$： $$\int{\sec x\tan xdx}=\sec x+c$$ - $13$： $$\int{\csc x\cot xdx}=-\csc x+c$$ - 练习： - $$\int{(2x^2-3x+5)dx}=\int{2x^2dx}-\int{3xdx}+\int{5dx}$$ $$=\frac{2}{3}x^3-\frac{3}{2}x^2+5x+c$$ - $$\int{\frac{(1-x)^2}{x\sqrt{x}}dx}=\int{\frac{x^2-2x+1}{x^{\frac{3}{2}}}dx}$$ $$=\int{(x^{\frac{1}{2}}-2x^{-\frac{1}{2}}+x^{-\frac{3}{2}})dx}$$ $$=\frac{2}{3}x^{\frac{3}{2}}-4x^{\frac{1}{2}}-2x^{-\frac{1}{2}}+c$$ - $$\int{\frac{x^4}{1+x^2}dx}=\int{\frac{x^4-1+1}{1+x^2}}$$ $$=\int{\frac{(x^2+1)(x^2-1)}{x^2+1}dx}+\int{\frac{1}{1+x^2}dx}$$ $$=\int{(x^2-1)dx}+\int{\frac{1}{1+x^2}dx}$$ $$=\int{x^2dx}-\int{1dx}+\int{\frac{1}{1+x^2}dx}$$ $$=\frac{1}{3}x^3-x+\arctan{x}+c$$ - $$\int{\cos^2{(\frac{x}{2})}dx}=\int{\frac{1+\cos x}{2}dx}$$ $$=\int{\frac{1}{2}dx}+\frac{1}{2}\cos xdx$$ $$=\frac{1}{2}x+\frac{1}{2}\sin x+c$$ - $$\int{\tan^2xdx}=\int{(\sec^2x-1)dx}$$ $$\int{\sec^2xdx}-\int{1dx}$$ $$=\tan x-x+c$$ - $$c^{'}{(x)}=50x-x^2,c(0)=100$$ $$c(x)=\int{c^{'}{(x)}dx}=\int{(50x-x^2)dx}=25x^2-\frac{1}{3}x^3+c$$ $$c(0)=100$$ $$c(x)=25x^2-\frac{1}{3}x^3+100$$ ## 积分法 $$\int{\cos xdx}=\sin x+c$$ $$\int{\cos x^2dx^2}=\sin x^2+c$$ $$\int{\cos f(x)df(x)}=\sin f(x)+c$$ $$\int{2x\cos x^2dx}=\int{(\cos x^2)2xdx}$$ $$=\int{\cos x^2}dx^2=\sin x^2+c$$ ### 第一换元积分法（凑微分） - 把 $d$ 外面的某项拿到 $d$ 里面。（变成原函数） - 凑基本积分公式。 $$\int{g(x)dx}=\int{f(g(x))g^{'}{(x)}dx}$$ $$=\int{f(g(x))dg(x)}=\int{f(k)dk}$$ $$=F(k)+c=F(g(x))+c$$ - 练习： - $$\int{3\cos{(3x)}dx}=\int{\cos{(3x)}d3x}=\sin3x+c$$ - $$\int{\frac{1}{3x+2}dx}=\frac{1}{3}\int{\frac{1}{3x+2}3dx}$$ $$=\frac{1}{3}\int{\frac{1}{3x+2}d(3x+2)}$$ $$=\ln{|3x+2|}+c$$ **$d$ 里面的常数随意加。** - $$\int{x\sqrt{1-x^2}dx}=\frac{1}{2}\int{\sqrt{1-x^2}dx^2}$$ $$=-\frac{1}{2}\int{\sqrt{1-x^2}d(-x^2)}$$ $$=-\frac{1}{2}\int{\sqrt{1-x^2}d(1-x^2)}$$ $$=-\frac{1}{2}\times \frac{2}{3}(1-x^{2})^{\frac{3}{2}}=-\frac{1}{3}(1-x^2)^{\frac{3}{2}}$$ - $$\int{xe^{x^2}dx}=\int{\frac{1}{2}e^{x^2}dx^2}$$ $$=\frac{1}{2}e^{x^2}+c$$ - $$\int{\sin x\cos xdx}$$ $$= \begin{cases} \int{\sin xd\sin x=\frac{1}{2}\sin^2 x+c_1}\\ \int{\frac{1}{2}\sin{2x}dx=\frac{1}{4}\int{\sin{2x}d2x}=-\frac{1}{4}\cos{2x}+c_2} \end{cases} $$ 其中 $c_1\not=c_2$，有时候一道题的解法并不唯一。 - $$\int{\frac{dx}{x(\ln x+1)}}$$ $$=\int{\frac{1}{(1+\ln x)}d(\ln x+1)}$$ 注意：这里没有绝对值，因为在题目中已经默认 $x>0$ 了。 $$=\ln|\ln x+1|+c$$ - $$\int{e^x\sqrt{1-e^x}dx}=\int{\sqrt{1-e^x}de^x}$$ $$=-\int{\sqrt{1-e^x}d(1-e^x)}=-\frac{2}{3}(1-e^x)^{\frac{3}{2}}+c$$ - $$\int{\frac{dx}{a^2+x^2}}=\int{\frac{1}{a^2}{\frac{dx}{1+\frac{x^2}{a^2}}}}$$ $$=\int{\frac{1}{a}\frac{d\frac{x}{a}}{1+(\frac{x}{a})^2}}=\frac{1}{a}\arctan{{\frac{x}{a}}}+c$$ - $$\int{\frac{dx}{x^2-a^2}}=\int{\frac{dx}{(x+a)(x-a)}}$$ $$=\int{\frac{1}{2a}(\frac{1}{x-a}-\frac{1}{x+a})dx}$$ $$=\frac{1}{2a}\int{\frac{1}{x-a}d(x-a)}-\frac{1}{2a}\int{\frac{1}{x+a}d(x+a)}$$ $$=\frac{1}{2a}(\ln|x-a|-\ln{|x+a|})+c$$ $$=\frac{1}{2a}\ln{|\frac{x-a}{x+a}|}+c$$ - 三角函数类重点公式： - $$\int{\tan xdx}=\int{\frac{\sin x}{\cos x}dx}=-\int{\frac{d\cos x}{\cos x}}=-\ln{|\cos x|}+c$$ - $$\int{\csc xdx}=\int{\frac{1}{\sin x }dx}$$ $$=\int{\frac{1}{2\sin{\frac{\pi}{2}\cos{\frac{\pi}{2}}}}dx}=\int{\frac{1}{2\frac{\sin{\frac{\pi}{2}}}{\cos{\frac{\pi}{2}}}\cos^2{\frac{\pi}{2}}}dx}$$ $$=\int{\frac{\sec^2{\frac{x}{2}}}{\tan \frac{x}{2}}d\frac{x}{2}}=\int{\frac{1}{\tan \frac{x}{2}}d\tan{\frac{x}{2}}}$$ $$=\ln{|\tan{\frac{x}{2}}|+c}$$ - $$\int{\sin^3{x}dx}=\int{\sin^2{x}\sin xdx}$$ $$=-\int{\sin^2{x}d\cos x}=-\int{(1-\cos^2x)d\cos x}$$ $$=-\cos x+\frac{1}{3}\cos^3x+c$$ - $$\int{\cos^2xdx}=\int{\frac{1+\cos2x}{2}dx}$$ $$=\int{\frac{1}{2}dx}+\frac{1}{4}\int{\cos2xd2x}$$ $$=\frac{1}{2}x+\frac{1}{4}\sin2x+c$$ - $$\int{\sin x\cos 3xdx}=\frac{1}{2}\int{(\sin 4x-\sin 2x)dx}$$ $$=\frac{1}{2}\int{\sin 4xdx}-\frac{1}{2}\int{\sin 2xdx}$$ $$=\frac{1}{8}\int{\sin 4xd4x}-\frac{1}{4}\int{\sin 2xd2x}$$ $$=-\frac{1}{8}\cos {4x}+\frac{1}{4}\cos{2x}+c$$ ### 第二换元积分 $$\int{f{(x)}dx}=^{x=g{(t)}}=\int{f{(g{(t)})}g^{'}{(t)}dt}$$ - 练习： - 换元： $$\int{}\frac{dx}{x\sqrt{2x-3}}$$ 设： $$t=\sqrt{2x-3},t^2=2x-3$$ $$x=\frac{1}{2}t^2+\frac{3}{2},dx=tdt$$ $$=\int{\frac{tdt}{(\frac{1}{2}t^2+\frac{3}{2})t}}=2\frac{dt}{3+t^2}$$ $$=\frac{2\sqrt{3}}{3}\int{\frac{d{\frac{t}{\sqrt{3}}}}{1+(\frac{t}{\sqrt{3}})^2}}$$ $$\frac{2\sqrt{3}}{3}\arctan{\frac{t}{\sqrt{3}}}+c$$ $$=\frac{2\sqrt{3}}{3}\arctan{\frac{\sqrt{6x-9}}{3}}+c$$ - 根换元： $$\int{\frac{dx}{\sqrt{x}+\sqrt[3]{x}}}$$ 设： $$t=\sqrt[6]{x},x=t^6$$ $$\sqrt{x}=t^3,\sqrt[3]{x}=t^2$$ $$dx=6t^5dt$$ $$=\int{\frac{6t^5dt}{t^3+t^2}}=\int{6\frac{t^3}{t+1}dt}$$ $$=6\int{\frac{t^3+1-1}{t+1}dt}$$ $$=6\int{(t^2-t+1-\frac{1}{t+1})dt}$$ $$=2t^3-3t^2+6t-6\ln|t+1|+c$$ $$=2\sqrt{x}-3\sqrt[3]{x}+6\sqrt[6]{x}-6\ln{|\sqrt[6]{x}+1|}+c$$ - 三角函数换元： $$\int{\sqrt{a^2-x^2}dx}(a > 0)$$ $$a^2-x^2\ge 0,x^2\le-a^2,-a\le x\le a$$ $$x=a\sin t(-\frac{\pi}{2}\le \sin t\le \frac{\pi}{2})$$ $$dx=a\cos tdt$$ $$\sqrt{a^2-a^2\sin^2t}=a\sqrt{\cos^2t}=a\cos t$$ $$=\int{a\times \cos t\times a\times \cos tdt}$$ $$=a^2\int{\cos^2 tdt}$$ $$=a^2(\frac{1}{2}t+\frac{1}{4}\sin{2t})+c$$ $$=\frac{a^2}{2}t+\frac{a^2}{2}\sin t\cos t+c$$ $$=\frac{a^2}{2}\arcsin{\frac{x}{a}}+\frac{a^2}{2}\frac{x}{a}\sqrt{1-\frac{x^2}{a^2}}+c$$ $$=\frac{a^2}{2}\arcsin{\frac{x}{a}}+\frac{x}{2}\sqrt{a^2-x^2}+c$$ 同样： $$\int{\frac{1}{\sqrt{a^2+x^2}}dx}(a > 0)$$ $$x=a\tan x$$ $$\sqrt{a^2+a^2\frac{\sin^2t}{\cos^2 t}}=a\frac{1}{\cos t}$$ 和： $$\int{\frac{1}{\sqrt{x^2-a^2}}dx},x^2-a^2>0,x^2>a^2$$ $x > a$ 或 $x < a x=a\sec t,0 < t <\frac{\pi}{2}

后面计算结果即可。

\int{\frac{x^3}{(x-1)^{100}}dx} x-1=t,x=t+1,dx=dt =\int{\frac{(t+1)^3}{t^{100}}dt}=\int{\frac{t^3+3t^2+3t+1}{t^{100}}dt} =\int{t^{-97}+3t^{-98}+3t^{-99}+t^{-100}dt} -\frac{1}{96}t^{-96}-\frac{3}{97}t^{-97}-\frac{3}{98}t^{-98}-\frac{1}{99}t^{-99}+c

最后将 t 换回 x 即可。

公式背过后会快很多：

\int{\frac{dx}{\sqrt{4x^2+9}}}=\frac{1}{2}\int{\frac{d(2x)}{\sqrt{(2x)^2+9}}}=\frac{1}{2}\ln{|2x+\sqrt{4x^2+9}|}+c

分部积分法

(uv)^{'}=u^{'}v+uv^{'} uv^{'}=(uv)^{'}-u^{'}v \int{uv^{'}dx}=\int{(uv)^{'}dx}-\int{u^{'}vdx} \int{udv=uv-\int{vdu}} =\frac{1}{2}(x^2\ln x-\int {x^2d\ln x}) =\frac{1}{2}(x^2\ln x-\int {x^2\frac{1}{x}dx}) =\frac{1}{2}(x^2\ln x-\frac{1}{2}x^2)+c

有理函数积分

\frac{P(x)}{Q(x)}

上下都是多项式。

大除法，多项式除多项式，将分子的最高次数降到 \le 分母最高次数。

将分子最高次项的系数凑成分母最高次项的系数，约掉。

目标状态。

\int{\frac{1}{ax^2+bx+c}dx}

同根 a(x-x_1)(x-x_2)=0

先配方，再结合分部积分法，就能解决大部分问题了。