图 G=(\mathcal{V,E}) 是由一组有限顶点 \mathcal V 和一组有限边 \mathcal E 组成的有序对。V 表示 G 中的顶点数量;E 表示边的数量。如果每条边都是一对无序的不同顶点,那么称图是 无向的 / undirected。如果每条边都是一对有序的不同顶点,那么图是 有向的 / directed。如果 (v,w) 是有向图中的边,我们说这条边 离开v进入w。如果 \mathcal V_1\subseteq\mathcal V_2 和 \mathcal E_1\subseteq\mathcal E_2,则图 G=(\mathcal V_1,\mathcal E_1) 是图 G_2=(\mathcal V_2,\mathcal E_2) 的子图。如果 G 是有向图,则 G 的 无向版本 / undirected version 是通过将 G 的每条边转换为无向边并删除重复边而形成的无向图。
一个顶点序列 v_i,1\le i\le n 与边 e_i,1\le i<n,若满足 e_i=(v_i,v_{i+1}),则被称为 G 中一条 _从 v_1 到 v_n 的路径 / path from v_1 to v_n_。存在一个顶点到其自身不包含边的路径。一个顶点 w 被称为从一个顶点 v可达的 / reachable,如果存在从 v 到 w 的路径。一条从一个顶点到其自身的路径被称为 闭合路径 / closed path。一条从 v 到 v 的闭合路径如果包含至少一条边,且其任意两条边不相同,且到达两次的顶点只有 v,则被称为一个 环 / cycle。两个互相是对方环排列的环被视为同一个环。我们用 p:v\Rightarrow^\ast w 表示 p 是从 v 到 w 的路径。
如果无向图 G 中的任何顶点都可以从任何其他顶点可达的,称 G 是 连通的 / connected。G 的最大连通子图是良定义且顶点不相交的 [38],被称为 G 的 连通分量 / connected components。如果 G 包含三个不同的顶点 x,v,w,使得 w 是从 v 可达的,但每条路径 p:v\Rightarrow^\ast w 都包含 x,则称 x 是 G 的 割点或分离点 / cutnode or separation point。如果 G 是连通的且不包含割点,称 G 是 双连通的 / biconnected。G 的最大双连通子图是良定义且边不相交的 [37],被称为 G 的 双连通分量 / biconnected components。如果 G 是双连通的,但包含四个不同的顶点 x,y,v,w,使得每条路径 p:v\Rightarrow^\ast w 都包含 x 或 y,则称 (x,y) 为 G 的 分离对 / separation pair。如果 G 是双连通的且不包含分离对,称 G 是 三连通的 / triconnected。图的三连通分量可以用多种方式定义 [8, 39]。我们可以通过考虑图的无向版本将这些定义扩展到有向图。
一个(有向的、有根的)树 / treeT 是带有一个特殊顶点的连通图,该特殊顶点被称为 根 / rootr,且满足每个 T 中的顶点都是从 r 可达的,没有边进入 r,恰好一条边进入 T 中的其余顶点。关系“(v,w) 是 T 的一条边”表示为 v\to w。关系“存在 T 中一条从 v 到 w 的路径”表示为 v\to^\ast w。如果 v\to w,称 v 是 w 的 父节点 / father 且 w 是 v 的 子节点 / son。如果 v\to^\ast w,称 v 是 w 的 祖先 / ancestor 且 w 是 v 的一个 后代 / descendant。每个顶点都是自身的祖先与后代。如果 v\to^\ast w 且 v\ne w,称 v 是 w 的 真祖先 / proper ancestor 且 w 是 v 的 真后代 / proper descendant。如果 T_1 是一棵树且 T_1 是树 T_2 的子图,称 T_1 是 T_2 的 子树 / subtree。如果树 T 是包含有向图 G 所有顶点的子图,称 T 是 G 的 生成树 / spanning tree。
图 G 是 平面的 / planar,当且仅当存在图的顶点和边到平面的映射,使得(1)每个顶点映射到一个不同的点,(2)每条边 (v,w) 映射到一条简单曲线上,顶点 v,w 映射到曲线的端点上,以及(3)不同边的映射只在其公共端点处重合。
满足上述条件的 G 的映射称为 G 的 平面嵌入 / planar embedding。(如果 G 是平面的,则存在 G 的平面嵌入使得边被映射为直线。)我们需要关于平面图的两个引理。
引理 1。如果 G 是平面的,E\le 3V-3。
若假设 V\ge3,界可以被加紧到 E\le 3V-6,但这对我们的目标不重要。
证明。这个引理是欧拉定理关于平面图中顶点、面和边的数量的直接结果 [35]。
引理 2。设 G 是嵌入在平面中的平面图。简洁起见,我们用嵌入来标识 G 的每条边。设 p_1,p_2,p_3 是三条从 x 到 y 的路径,满足任意两条路径的公共点只有 x,y。设 (x,v_1),(x,v_2),(x,v_3) 分别为 p_1,p_2,p_3 的第一条边,设 (w_1,y),(w_2,y),(w_3,y) 分别为 p_1,p_2,p_3 的最后一条边。若在 x 周围这些边在平面中的出现顺序按顺时针为 (x,v_1),(x,v_2),(x,v_3),则在 y 周围这些边的出现顺序按顺时针为 (w_1,y),(w_3,y),(w_2,y)(图 2)。
证明。这是 Jordan 曲线定理的推论,该定理指出,一条简单闭合曲线恰好将平面划分为两个连通的区域。我们接受该引理而不去证明;Jordan 曲线定理很难证明。(见 [40, 41]。)
图算法需要一种系统的方法来探索图。我们使用一种称为 深度优先搜索 / depth-first search 的方法。我们从 G 的一割顶点 s 开始,选择一条从 s 出发的边。访问边会得到一个新顶点。一般来说,我们通过选择和遍历从最近到达的仍有未访问的边的顶点开始的未访问的边来继续搜索。如果 G 是连通的,则每条边将被访问一次。
如果 G 是无向的,则 G 的深度优先搜索会给 G 的每条边上确定一个方向,该方向由搜索过程中访问边的方向给出。因此,搜索将 G 转化为有向图 G'。搜索还将(现在变为有向的)边分为两类:一组 树边 / tree arcs,定义了 G' 的生成树 T,以及一组满足 T 中 w\to^\ast v 的 frond(v,w) [6]。frond (v,w) 用 v-\to w 表示。边可以这样划分的有向图 G' 称为 plam tree。深度优先搜索很重要,因为 palm tree 中的路径结构非常简单。
begin comment routine for depth-first search of a graph G represented by adjacency lists A(v). Variable n denotes the last number assigned to a vertex;\
$\quad$**procedure** DFS(v, u); **comment** vertex u is the father of vertex v in the spanning tree being constructed;\
$\quad$**begin**\
$\qquad$n := NUMBER(v) := n + 1;\
$\qquad$a: **comment** dummy statement;\
$\qquad$**for** $w\in A(v)$ **do begin**\
$\qquad\quad$**if** NUMBER(w) = 0 **then begin**\
$\qquad\qquad$**comment** a is a new vertex;\
$\qquad\qquad$mark (v, w) as a tree arc;\
$\qquad\qquad$DFS(w, v);\
$\qquad\qquad$b: **comment** dummy statement;\
$\qquad\quad$**end**;\
$\qquad\quad$**else if** NUMBER(w) < NUMBER(v) and w $\ne$ u **then begin**\
$\qquad\qquad$**comment** this test is necessary to avoid exploring an edge in both directions;\
$\qquad\qquad$mark (v, w) as a frond;\
$\qquad\qquad$c: **comment** dummy statement;\
$\qquad\quad$**end**;\
$\qquad$**end**;\
$\quad$**end**;\
$\quad$**for** i := 1 **until** V **do** NUMBER(i) := 0;\
$\quad$n := 0;\
$\quad$**comment** the search starts at vertex s;\
$\quad$DFS(s, 0);\
**end**;
引理 3。上述过程正确地执行了无向图的深度优先搜索,如果图有 $V$ 个顶点和 $E$ 条边,该过程需要 $O(V+E)$ 时间。且顶点的标号满足:如果 $(v,w)$ 是树边,那么 $NUMBER(v)<NUMBER(w)$;如果 $(v,w)$ 是 frond,$NUMBER(w)<NUMBER(v)$。
### 4. 平面性算法概述
本节简要介绍平面性算法背后的思想。第 5 节和第 6 节开发了详细分量,第7 节全面介绍了算法。该算法的第一步是去除边太多的图。我们计算图中的边数,如果计数超过 $3V-3$,我们就声明图是非平面的。接下来,我们将图划分为双连通分量。(当且仅当图的所有双连通分量都是平面的时,图才是平面的 [35]。)参考文献 [5, 6] 描述了如何在 $O(V+E)$ 时间内将图划分为双连通分量。然后我们测试每个分量的平面性。
为了测试分量的平面性,我们调用 DFS,将图转换为 palm tree $P$ 并对顶点进行编号。现在我们使用 Auslander, Parter 和 Goldstein 的算法。该算法在图中找到一个环并将其删除,留下一组不相连的部分。然后,该算法检查每个部分加上原始环的平面性(通过递归调用自身),并确定部分的嵌入是否可以组合起来,从而得到整个图的嵌入。让我们分别考察这个过程的找环部分和平面性测试部分。
为测试平面性,算法的每次递归调用要求我们找到图的部分的一个环。这个环将包含之前找到的循环中不包含的边的构成的简单路径,以及旧环中的边的一条简单路径组成。我们使用深度优先搜索将图划分为简单的路径,这些路径可以被组装成平面性测试所需的环。我们需要第二次搜索来找到路径,因为如果平面性测试要有效,搜索必须以特殊的顺序进行。第 5 节详细描述了路径查找过程,并证明了生成路径的一些重要性质。
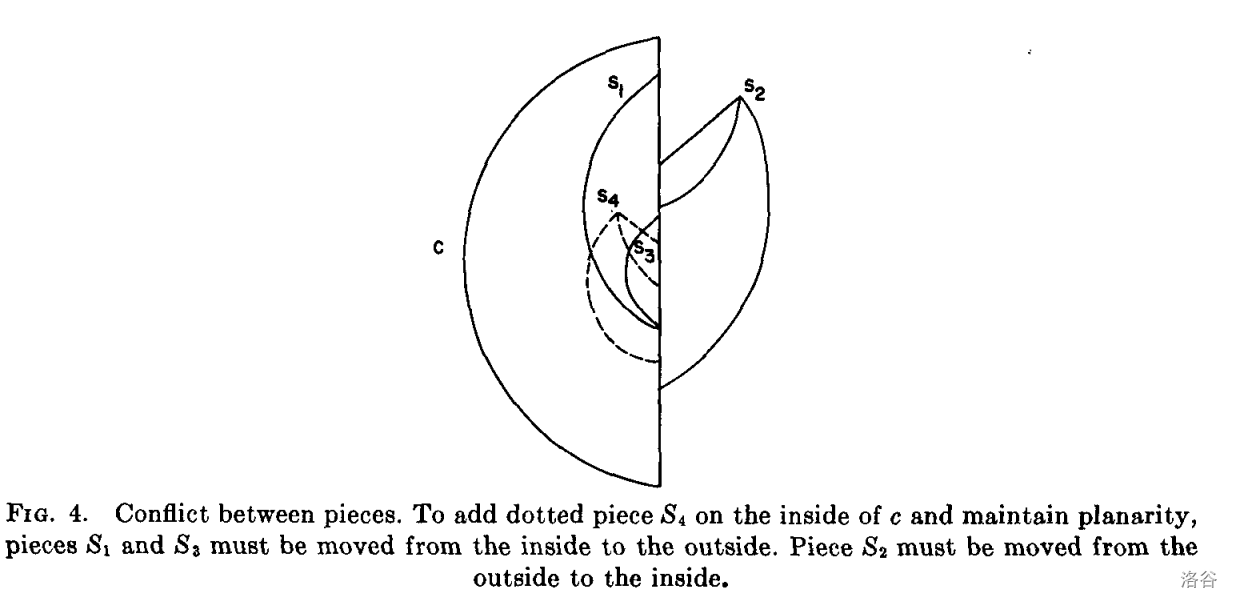
现在考虑第一个环 $c$。它将包含一个树边的序列,后面是 $P$ 中的一个 frond。顶点的编号满足顶点沿环按数字顺序排列。不属于循环的每一部分都将由一个 frond $(v,w)$ 组成,或者由一条树边 $(v,w)$ 加上一棵根为 $w$ 的子树,再加上从子树中引出的所有 frond 组成。我们处理这些部分,并按照 $v$ 降序将它们添加到平面表示中。根据 Jordan 曲线定理,每个片段都“在 $c$ 内”或“在 $c$ 外”。当我们添加一个部分时,某些部分必须从 $c$ 的内部移动到外部或从外部移动到内部。(见图 4。)我们持续添加新部分,并在必要时移动旧部分,直到无法添加部分或整个图被嵌入平面中。第 6 节描述了在移动部分时跟踪部分所需的数据结构。下面是整个算法的概述。
**procedure** PLANARITY(G);\
**begin comment** an outline of the planarity algorithm;\
$\quad$**integer** E;\
$\quad$E := 0;\
$\quad$**for** each edge of G **do begin**\
$\qquad$E := E + 1;\
$\qquad$**if** E > 3V - 3 **then go to** nonplanar;\
$\quad$**end**;\
$\quad$divide G into biconnected components;\
**for** each biconnected component G **do begin**\
$\qquad$explore C to number vertices and transform C into a palm tree P;\
$\qquad$find a cycle c in P;\
$\qquad$construct planar representation for c;\
$\qquad$**for** each piece formed when c is deleted **do begin**\
$\qquad\quad$apply algorithm recursively to determine if piece plus cycle is planar;\
$\qquad\quad$**if** piece plus cycle is planar **and** piece maybe added to planar representation **then** add it **else**\
$\qquad\qquad$**go to** nonplanar;\
$\quad\quad$**end**;\
$\quad$**end**;\
**end**;
### 5. 路径寻找
此后我们假设 $G$ 是已被 DFS 探索、顶点被标号并构造了一棵 palm tree $P$ 的双连通图。我们将用顶点的标号标识顶点。如果 $v$ 是顶点,设 $S_v=\{w|\exists u(v\to^\ast u\land u-\to w)\}$。则 $S_v$ 是从 $v$ 的后代通过 frond 可达的节点的集合。令:
$$\begin{cases}\operatorname{LOWPT1}(v)=\min(\{v\}\cup S_v)\\\operatorname{LOWPT2}(v)=\min(\{v\}\cup(S_v-\{\operatorname{LOWPT1(v)}\}))\end{cases}$$
$\operatorname{LOWPT1}(v)$ 是 $v$ 后代通过一条 frond 可达的小于 $v$ 的最小的顶点,且 $\operatorname{LOWPT2}(v)$ 是 $v$ 后代通过一条 frond 可达的低于 $v$ 的第二小的顶点。按照惯例,如果这些值未定义,那么这些值都等于 $v$。除非 $\operatorname{LOWPT1}(v)=\operatorname{LOWPT2}(v)=v$,那么 $\operatorname{LOWPT1}(v)\ne\operatorname{LOWPT2}(v)$。节点 $v$ 的 $\operatorname{LOWPT}$ 值只取决于 $v$ 的子节点的 $\operatorname{LOWPT}$ 值与离开 $v$ 的 frond;因此很容易使用 DFS 计算 $\operatorname{LOWPT}$ 值。在 DFS 中的无用语句 a, b, c 处插入下面的语句可以得到一个计算 $\operatorname{LOWPT}$ 值的过程。
**comment** additions to DFS for calculation of LOWPT1, LOWPT2;\
a: LOWPT1(v) := LOWPT2(v) := NUMBER(v);\
b: **if** LOWPT1(w) < LOWPT1(v) **then begin**\
$\quad$LOWPT2(v) := min{LOWPTl(v), LOWPT2(w)};\
$\quad$LOWPT1(v) : = LOWPT1(w) ;\
**end**\
**else if** LOWPT1(w) := LOWPT1(v) **then**\
$\quad$LOWPT2(v) := min{LOWPT2(v), LOWPT2(w)};\
**else** LOWPT2(v) := min{LOWPT2(v), LOWPT1(w)};\
c: **if** NUMBER(w) < LOWPT1(v) **then begin**\
$\quad$LOWPT2(v) := LOWPT1(v);\
$\quad$LOWPT1(v) := NUMBER(w);\
**end**\
**else if** NUMBER(w) > LOWPT1(v) **then**\
$\quad$LOWPT2(v) := min{LOWPT2(v), NUMBER(w)};
很容易验证按上述修改后的 DFS 会在 $O(V+E)$ 时间内正确计算出 $\operatorname{LOWPT}$ 值。(见 [6, 8, 29]。)如 [5, 6] 中所述,$\operatorname{LOWPT1}$ 可以用于检测 $G$ 的双连通性。这是一个重要的相关引理:
引理 4。若 $G$ 是双连通的,$v\to w$,除非 $v=1$,那么 $\operatorname{LOWPT1}(w)<v$,若 $v=1$,则 $\operatorname{LOWPT1}(w)=v=1$。且 $\operatorname{LOWPT1}(1)=1$。
证明。见 [6]。
为了生成路径,我们根据 $\operatorname{LOWPT}$ 值对 $P$ 的邻接链表排序,并进行另一次 DFS。设 $\phi$ 是如下定义在 $P$ 的边 $(v,w)$ 上的函数:
$$\phi((v,w))=\begin{cases}2w&v-\to w\\2\operatorname{LOWPT1}(w)&v\to w\land\operatorname{LOWPT2}(w)\ge v\\2\operatorname{LOWPT1}(w)+1&v\to w\land\operatorname{LOWPT1}(w)<v\end{cases}$$
对每条 $P$ 中的边计算 $\phi((v,w))$,按 $\phi$ 自增顺序排序邻接链表,使用基数排序达到 $O(V+E)$ 时间界。可以这样实现:
**comment** construction of ordered adjacency lists;\
**for** i := 1 until 2V + 1 **do** BUCKET(i) := the empty list;\
**for** (v, w) an edge of G **do begin**\
$\quad$compute $\phi((v,w))$;\
$\quad$add (v, w) to $\operatorname{BUCKET}(\phi((v,w)))$;\
**end**;\
**for** v := 1 **until** V **do** A(v) := the empty list;\
**for** i := 1 **until** 2V + 1 **do**\
$\quad$**for** $(v,w)\in\operatorname{BUCKET}(i)$ **do** add w to end of A(v);
该过程给出了一组表示 $P$ 的正确排序的邻接链表。现在,我们通过使用新的邻接链表对 $P$ 应用深度优先搜索来生成路径。每次我们遍历一条边时,都会将其添加到正在构建的路径中。每次我们穿过一条 frond 时,该 frond 都会成为当前路径的最后一条边。下一条边开始一条新路径。因此,每条路径都由一个树边的序列和一条 frond 组成。为了实现这一点,我们使用以下步骤:
**begin comment** routine to generate paths in a biconnected palm tree with specially ordered adjacency lists A(v). Vertex s is a global variable, the start vertex of the current path, and is initialized to 0;\
**procedure** PATHFINDER(v);\
$\quad$**for** $w\in A(v)$ do\
$\qquad$**if** $v\to w$ **then begin**\
$\qquad\quad$**if** s = 0 **then begin**\
$\qquad\qquad$s := v;\
$\qquad\qquad$start new path;\
$\qquad\quad$**end**;\
$\qquad\quad$add (v, w) to current path;\
$\qquad\quad$PATHFINDER(w);\
$\qquad$**end**\
$\qquad$**else begin**\
$\qquad\quad$**comment** $v-\to w$;\
$\qquad\quad$**if** s = 0 **then begin**\
$\qquad\qquad$s := v;\
$\qquad\qquad$start new path\
$\qquad\quad$**end**;\
$\qquad\quad$add (v, w) to current path;\
$\qquad\quad$output current path;\
$\qquad\quad$s := 0;\
$\qquad$**end**;\
$\quad$s := 0;\
$\quad$**comment** vertex 1 is the start vertex of the search;\
$\quad$PATHFINDER(1)\
**end**;
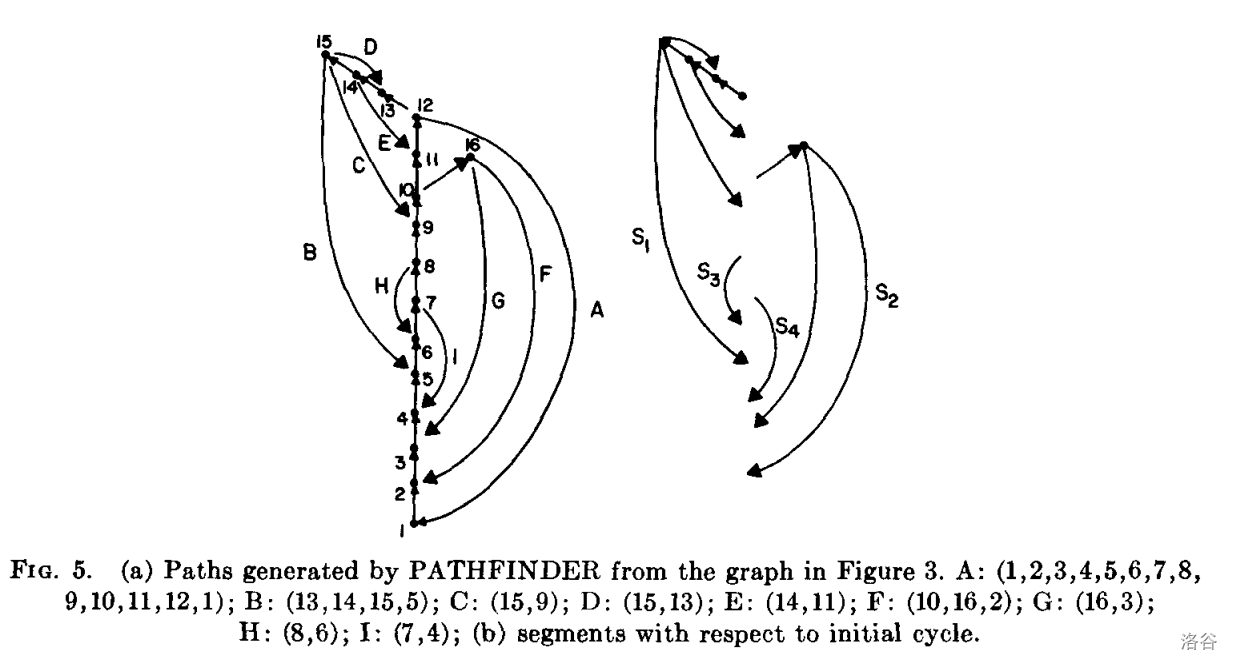
以这种方式生成的路径具有几个重要属性,这些属性在以下引理中被总结。图 5 显示了从图 3 中的图生成的一组路径。程序 PATHFINDER 需要 $O(V+E)$ 时间在有 $V$ 个顶点和 $E$ 条边的图中查找路径;添加到路径的边总数为 $O(V+E)$,PATHFINDER 只是一个有一些额外的操作来构造路径的深度优先搜索。事实上,对于平面性算法,我们只需要知道每条路径的起始顶点和结束顶点。
引理 5。设 $p:s\Rightarrow^\ast f$ 为一条生成的路径。若我们考虑当 $p$ 中第一条边被遍历时所有没被用到的 frond,则 $f$ 是通过 $s$ 的任意后代通过一条这样的 frond 到达的最小的顶点。如果 $n\ne s,v\ne f$,且 $v$ 在路径 $p$ 上,则 $f$ 是从 $v$ 的一个后代通过任意 frond 可达的(当 $p$ 的第一条边被遍历时,所有从 $v$ 的后代出发的 frond 都没有被使用)。
证明。该引理是邻接链表序列顺序的直接推论。
引理 6。设 $p:s\Rightarrow^\ast f$ 为一条生成的路径。则 $P$ 的生成树中 $f\to^\ast s$。若 $p$ 是第一条路径,则 $p$ 是环;否则 $p$ 是简单路。若 $p$ 不是初始路径,$p$ 与之前生成的路径包含恰好两个相同的顶点($f$ 与 $s$)。
证明。设 $p:s\Rightarrow^\ast f$ 为任意一条生成的路径。若该路径仅包含一条 frond,则该路径是简单路且 $f\to^\ast s$。若路径包含一条树边,设 $s\to v$ 是第一条树边。则由引理 5,$f=\operatorname{LOWPT1}(v)$。若 $s=1$ 路径是环,若 $s>1$,由引理 4,路径是简单路。任意情况中 $f\to^\ast s$。
引理 7。设 $p_1:s_1\Rightarrow^\ast f_1,p_2:s_2\Rightarrow^\ast f_2$ 为两条生成的路径。若 $p_1$ 在 $p_2$ 前生成,且 $s_1$ 是 $s_2$ 的祖先,则 $f_1\le f_2$。
证明。$p_2$ 的终止 frond 导向一个在 $p_1$ 被生成时没有用到的 $s_1$ 的后代。由引理 $5$ 可知 $f_1\le f_2$。
引理 8。设 $p_1:s\Rightarrow^\ast f,p_2:s\Rightarrow^\ast f$ 为两条由相同起点与终点的生成的路径。设 $v_1$ 为 $p_1$ 的第二个顶点且 $v_2$ 为 $p_2$ 的第二个顶点。设 $p_1$ 在 $p_2$ 前生成且 $v_1\ne f$ 且 $\operatorname{LOWPT2}(v_1)<s$。那么 $v_2\ne f,\operatorname{LOWPT2}(v_2)<s$。
证明。因为 $p_1$ 早于 $p_2$ 生成,所以 $A(s)$ 中 $v_1$ 一定出现在 $v_2$ 前。该引理由 $A(s)$ 的顺序限制即可证明。
引理 8 是我们在路径寻找算法中引入 $\operatorname{LOWPT2}$ 值的原因。当我们考虑路径在平面中的嵌入时,我们会知道为什么这个引理很重要。
设 $p:s\Rightarrow^\ast f$ 为一条生成的路径,我们可以通过将一组树边 $f\to^\ast s$ 加入 $p$ 形成一个环。这样形成的环就是由 Auslander-Parter-Goldstein 平面性算法的递归调用所生成的环。这些环有一个简单的结构;每个环都对应于 $P$ 一条 frond。在考虑路径的嵌入前我们需要一些别的定义。设 $p:s\Rightarrow^\ast f$ 为路径寻找算法生成的一条简单路,设 $p_0:s_0\Rightarrow^\ast f_0$ 为包含 $s$ 的最早被生成的路径。若 $f_0<f$ 则 $p$ 被称为 _正常路径 / normal path_。若 $f_0=f$ 则 $p$ 被称为 _特殊路径 / special path_。由引理 7,$f_0>f$ 的情况不可能出现。
### 6. 嵌入路径
若 $G$ 是带有由路径寻找算法生成的一组路径的双连通图,我们通过尝试在平面中逐次加入路径来判定 $G$ 的平面性。设 $c$ 为第一条路径(一个环)。这个环包含一组树边 $1\to v_1\to\cdots\to v_n$,后为一条 frond $v_n\to1$。顶点的编号满足 $1<v_1<\cdots<v_n$。当删除 $c$ 时,$G$ 分裂为若干连通部分,这些部分被称为 _段 / segments_。每个段 $S$ 要么仅包含一条 frond $(v_i,w)$ 要么包含树边 $(v_i,w)$ 加上以 $w$ 为根的子树加上所有从子树出发的 frond。路径生成的顺序满足一个段中的所有路径都在其余段的路径被生成前生成,且路径按照 $v_i$ 递减顺序探索。
根据 Jordan 曲线定理。一个段必须完全嵌入到 $c$ 的一侧。一个段通过一条从 $c$ 出发的边 $(v_i,w)$ 与一条或更多从 $c$ 出发的 frond 附加到 $c$。(如果该段只由一条 frond 组成,该 frond 的两个端点都在 $c$ 上。)如果 $v_i$ 周围边的出现顺序(顺时针)为 $(v_{i-1},v_i),(v_i,w),(v_i,v_{i+1})$,我们称段 $S$ 被嵌入到($c$ 的)_左侧 / left_。如果 $v_i$ 周围边的出现顺序为 $(v_{i-1},v_i),(v_i,v_{i+1}),(v_i,w)$,我们称段 $S$ 被嵌入到 _右侧 / right_。若所属的段属于 $c$ 的左侧(右侧),我们称进入 $c$ 的 frond 被嵌入到 _左侧 / left(右侧 / right)_。若 $(x,v_j)$ 从左侧进入 $c$,则由引理 2,$v_j$ 周围边的出现顺序为 $(v_{j-1},v_j),(x,v_j),(v_j,v_{j+1})$。
设 $c$ 与 $S$ 前被探索的段已经被嵌入到平面中。设 $p:v_i\Rightarrow^\ast v_j$ 为 $S$ 中找到的第一条路径。下面的引理给出了将 $p$ 加入到嵌入中的充要条件。
引理 9。路径 $p:v_i\Rightarrow^\ast v_j$ 可以通过将其放置在 $c$ 的左侧(右侧)将其添加入平面嵌入中当且仅当之前在左侧(右侧)嵌入的 frond 中不存在 $(x,v_k)$ 满足 $v_j<v_k<v_i$。
证明。如果没有 frond 满足条件,则没有任何类型的嵌入边在 $v_j$ 和 $v_i$ 之间在左侧(右侧)进入或离开 $c$。如果路径 $p$ 足够靠近 $c$,即可嵌入到 $c$ 的左侧(右侧)。相反,假设我们想在左测嵌入 $p$,但一些 $v_j<v_k<v_i$ 的已嵌入的 frond $(x,v_k)$ 从左侧进入 $c$。要么 $x$ 位于 $c$ 上(设 $x=v_l$),要么 $(x,v_k)$ 是第一条边为 $(v_l,w)$ 的段 $S'$ 的一部分。我们根据路径生成的顺序知道 $v_l\ge v_i$。我们必须考虑两种情况。
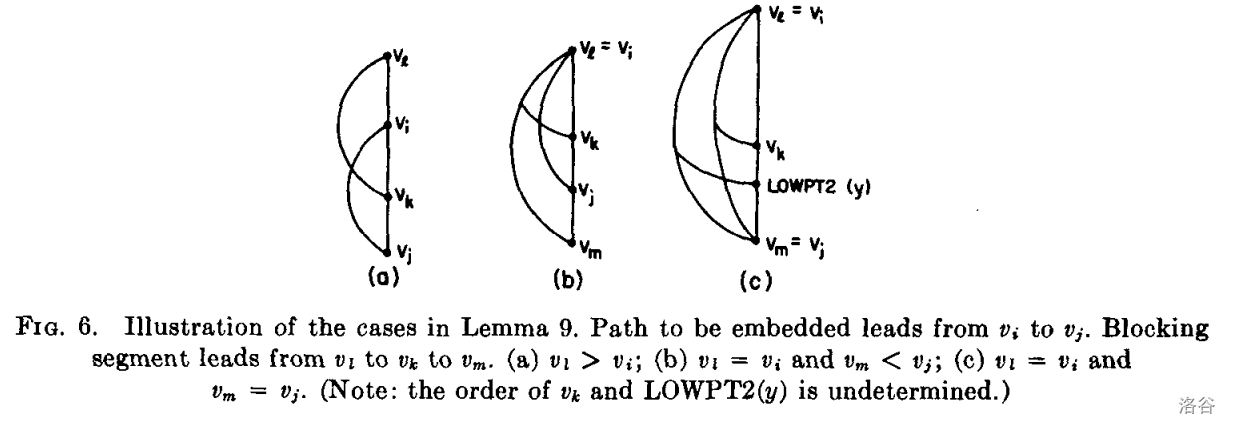
情况 1。$v_l>v_i$(图 6 (a) )。设 $p$ 在左侧嵌入。由 $p$,一条 $S'$ 中连接 $v_l,v_k$ 的路径,与从 $v_j$ 到 $v_l$ 的树边的路径,我们可以构造三条违反引理 2 的从 $v_i$ 出发到达 $v_k$ 的路径。因此 $p$ 不能在左侧嵌入。
情况 2。$v_l=v_i$。设 $p_1:v_l\Rightarrow^\ast v_m$ 为 $S'$ 中第一条被找到的路径。由引理 7,我们有 $v_m\le v_j$。有两种子情况。
子情况 A。$v_m<v_j$(图 6 (b) )。设 $p$ 在左侧嵌入,由路径 $p$,一条 $S'$ 中连接从 $v_k$ 出发到达 $v_m$ 的路径,与从 $v_m$ 出发到达 $v_i$ 的树边的路径我们可以形成三条违反引理 2 的从 $v_k$ 出发到达 $v_j$ 的路径。因此 $p$ 不能在左侧嵌入。
子情况 B。$v_m=v_j$(图 6 (c) )。设 $y$ 为 $p$ 上第二个顶点($w$ 已被定义为 $p_1$ 的第二个顶点)。因为段 $S'$ 包含 frond $(x,v_k)$ 且$w\ne v_m$ 且 $\operatorname{LOWPT2}(w)<v_i$。比较 $p,p_1$ 并应用引理 8,我们有 $y\ne v_j$ 且 $\operatorname{LOWPT2}(y)<v_i$。更进一步,因为 $\operatorname{LOWPT1}(y)=v_j$,通过引理 5,我们有 $\operatorname{LOWPT2}(y)>v_j$。设 $p$ 在左侧嵌入。由 $p,p_1$,一条从 $p$ 上顶点到 $\operatorname{LOWPT2}(y)$ 的路径,一条从 $p_1$ 上顶点到 $v_k$ 的路径,与一条连接 $v_k,\operatorname{LOWPT2}(y)$ 的(可能为空的)树边的路径,我们可以形成违反引理 2 的三条路径,因此 $p$ 不能在左侧嵌入。
我们使用引理 9 来判定平面性,方法如下:首先,我们将环 $c$ 嵌入到平面中。然后,我们按照路径寻找中探索的顺序一次嵌入一个段。为了嵌入一个段 $S$,我们在其中找到一条路径,比如 $p$。我们选择从一边,比如从左边,嵌入 $p$。我们将 $p$ 与之前嵌入的 frond 进行比较,以确定 $p$ 是否可以嵌入。如果不能直接嵌入,我们将有阻挡 $p$ 的 frond 的段从左侧移动到右侧。如果 $p$ 可以在移动段后嵌入,我们就嵌入 $p$。但是,如果我们将段从左侧移动到右侧,我们可能需要将其它段从右侧移动到左侧。因此,可能无法嵌入 $p$。如果是这样,我们断言该图是非平面的。如果 $p$ 可以嵌入,我们基本上通过递归使用算法试图嵌入 $S$ 的其余部分。然后我们尝试嵌入下一个段。
我们需要一些好的数据结构来有效地实现这种方法。如果我们要嵌入一个从顶点 $v_i$ 开始的段,我们必须知道从 $1$ 到 $v_i$ 的树路径上的哪些顶点有从左侧或右侧进入的 frond。为此,我们使用两个栈($L$ 和 $R$)。栈 $L$ 将(按顺序)包含满足 $1\to^\ast v_k\to^\ast v_i$ 的 $v_i$,与一些从左侧嵌入的进入 $v_k$ 的 frond。$L$ 只需要为每个有一条指向 $v_k$ 的 frond 的段包含一次顶点 $v_k$,但有时同一个段中的两条 frond 可能会指向相同的顶点 $v_k$,这可能会导致 $v_k$ 在栈上出现两次,即使 $v_k$ 只代表一个段。栈 $R$ 对嵌入的在右侧嵌入 $c$ 的 frond 执行与 $L$ 相同的功能。
栈 $L,R$ 必须以四种方式更新:
1. 在探索并嵌入从 $v_{i+1}$ 开始的所有段后,必须删除 $L$ 和 $R$ 中出现的所有 $v_i$,因为尚未探索的段从不大于 $v_i$ 的顶点开始。这类更新需要删除 $L,R$ 顶部的一些元素。
2. 如果 $p:s\Rightarrow^\ast f$ 是段 $S$ 中的第一条路径,且 $p$ 是正常路径,则当嵌入 $p$ 时,必须将 $f$ 加入栈中。(由于 $s$ 位于 $c$ 上,$f>1$ 当且仅当 $p$ 是正常路径。)根据引理 9,当 $L(R)$ 上的每个顶点都不大于 $f$ 时,$p$ 只能嵌入到左侧(右侧),因此 $f$ 可以添加到 $L(R)$ 的顶部。
3. 该算法的递归应用必须为段 $S$ 中的其余路径添加元素。我们稍后将研究该算法的递归应用。
4. 随着段的移动,相应的元素必须从一个栈转移到另一个栈。比如从左侧嵌入一条 frond,由引理 2,这迫使同一个段中的 frond 嵌入左侧,并由引理 9,可能迫使其余段中的 frond 嵌入右侧。设 _块 / block_ $B$ 是 $L,R$ 上与 frond 对应的最大元素集,使得任何一个 frond 的位置都决定了所有其他 frond 的位置。块会随着栈的变化而变化,但块总是对栈元素进行分区。此外,这些块具有由下一个引理给出的简单结构。
引理 10。设 $B$ 为一个块。则 $B\cap L(B\cap R)$ 在 $L(R)$ 上相邻。且存在 $c$ 上的顶点 $v_j,v_k$ 满足对于 $v_l\in L\cap R$ 有:
1. 如果 $v_j<v_l<v_k$,则 $v_l\in B$。
2. 如果 $v_l<v_j$ 或 $v_l>v_k$,则 $v_l\notin B$。
证明。对嵌入的段的数量和从 $L,R$ 中删除的元素数进行归纳。在嵌入任何段之前,引理肯定是正确的,因为两个栈都是空的。如果引理在从 $L,R$ 的顶部删除所有 $v_i$ 前为真,那么引理在删除后肯定为真,因为从 $L,R$ 中删除 $v_i$ 只可能导致完整的块(仅由 $v_i$ 组成)被删除,并导致剩余的顶部块失去其顶部顶点的出现。
假设在嵌入段 $S$ 之前引理为真。设 $p:s\Rightarrow^\ast f$ 为 $S$ 中的第一条路径。假设 $S$ 嵌入到左侧。当与 $S$ 对应的元素被添加到 $L$ 中时,根据引理 9,这形成一个新的块 $B$,其中包含与 $S$ 对应的元素,还包含 $R$ 中具有满足 $f<v_l<S$ 的元素 $v_l$ 的所有旧块 $B$。设 $v_0$ 是任何这类块 $B$ 中的最小元素 $v_l$。其余旧块中的所有元素 $v_m$ 都满足 $v_m=\min(v_0,f)$。新块 $B'$ 由位于 $L,R$ 上的旧块以及位于 $L$ 上的与 $S$ 对应的新块组成。因此,块 $B'$ 满足 $v_j=\min(v_0,f)$ 和 $v_k=s$ 的引理。其他旧块保持不变。引理可由对嵌入的段的数量和从 $L,R$ 中删除的元素数进行归纳得到。
引理10表明了我们如何跟踪这些块。这些块为我们提供了足够的信息,可以轻松地将元素从一个栈移动到另一个栈。我们使用链表来存储 $L,R$。然后,为了在栈之间切换严肃块,我们只需要在块的开头和结尾切换链表指针。我们使用栈 $B$ 来跟踪块。$B$ 的每个元素代表一个块,是一个有序对 $(x,y)$,其中 $x$ 指向 $L$ 上最后一个块的元素,$y$ 指向 $R$ 上最后一个块的元素。如果 $x=0(y=0)$,则该块在 $L(R)$ 上没有元素。下面的过程实现了嵌入算法。第 $7$ 节详细介绍了必要的列表处理操作。
procedure EMBED; **begin**\
$\quad$**comment** routine to embed a properly ordered biconnected graph in the plane, if possible;\
$\quad$L := R := B := the empty stack;\
$\quad$find first cycle c;\
$\quad$**while** some segment is unexplored **do begin**\
$\qquad$initiate search for path in next segment S;\
$\qquad$when backing down tree arc $v\to w$ delete entries on L and R and blocks on B containing vertices no smaller than v;\
$\qquad$let $p:s\Rightarrow^\ast f$ be first path found in segment S;\
$\qquad$**while** position of top block determines position of p **do begin**\
$\qquad\quad$delete top block from B;\
$\qquad\quad$**if** block entries on left **then** switch block of entries from L to R and from R to L by switching list pointers;\
$\qquad\quad$**if** block still has an entry on left in conflict with p then go to nonplanar;\
$\qquad$**end**;\
$\qquad$**if** p is normal **then** add last vertex of p to L;\
$\qquad$add new block to B corresponding to p and blocks just removed from B;\
$\qquad$d: apply algorithm recursively to embed other paths in S;\
$\qquad$**comment** details of the recursive application are discussed later. After completion of this step, other paths in S which lead to ancestors of S will be represented on L. One new block corresponding to these paths will appear on B;\
$\qquad$combine top two blocks on B;\
$\quad$**end**;\
**end**;
引理 11。$G$ 是平面的当且仅当过程 EMBED 终止。否则,过程将分支到“非平面”位置。
证明。EMBED 是前面描述的算法的直接实现。在任何时候,栈 $L,R$ 都包含嵌入在环 $c$ 左右两侧的 frond 的元素,栈 $B$ 包含有关每个元素块结束的信息。引理 9 用于判定平面性,引理 10 用于在过程执行时修改块。假设步骤 d(算法的递归应用)正确实现,则可以通过归纳法直接证明在块中嵌入任何 frond 完全决定了块中所有 frond 的嵌入,以及从一个块中嵌入 frond 不会限制不在块中的 frond 的嵌入。根据引理 9 和 10,该程序正确地判定了平面性。
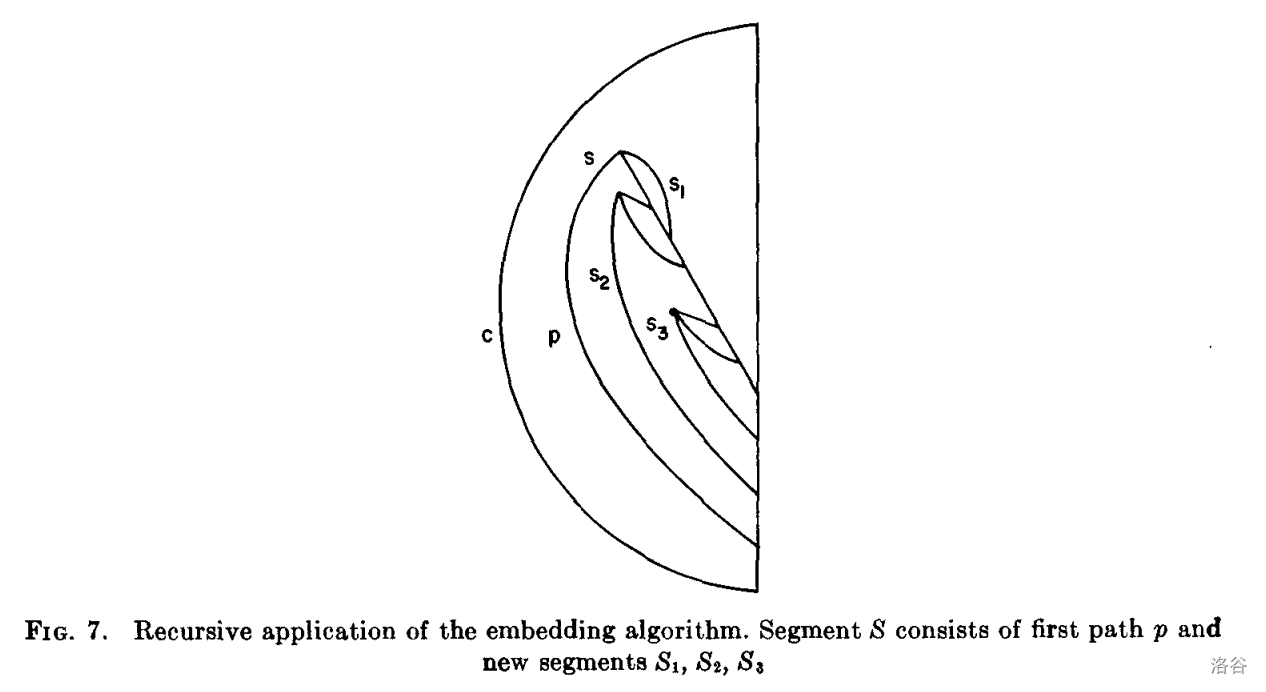
考虑在段中嵌入第二条和后续路径。假设环 $c$,$S$ 之前的所有段和 $S$ 中的第一条路径 $p:s\Rightarrow^\ast f$ 都已嵌入。很容易看出,当且仅当 $S,c$ 一起形成平面图时,$S$ 的其余部分才能被添加到嵌入中。(事实上,这是根据 Auslander 和 Parter 的结果 [1] 得出的。)图 7 显示了 $S,c$。路径 $p$ 和从 $f$ 到 $s$ 的树边路径形成了一个环 $c'$,用于递归应用嵌入算法。
在 EMBED 将 $p$ 嵌入左侧后,$L$ 上的顶部元素是 $f$。引理 5 中,$S$ 中的所有 frond 都指向不小于 $f$ 的顶点。假设我们在 $R$ 的顶部放置一个栈结束标记,并递归应用嵌入算法来确定循环 $c'$ 加上删除 $c'$ 时形成的 $S$ 中的段是否可以嵌入到平面中。如果递归成功完成,栈 $L,R$ 将包含与 $S$ 中正常路径的终止 frond 对应的元素,栈 $B$ 可能包含一些新块。当且仅当没有新块同时在 $R,L$ 上有元素时,环 $c$ 的其余部分可以添加到 $S,c'$ 的嵌入中。如果没有新块同时在 $R,L$ 上有元素,那么任何在 $R$ 上有元素的新块都可以移动到 $L$,结果是没有新块会在 $R$ 上有元素。
因此,为了完成对 $c,S$ 的平面性的判定,我们必须尝试将新块从 $R$ 移动到 $L$。要继续算法的顶级应用,我们必须将所有新块组合成一个与 $S$ 减去 $p$ 中的路径对应的块,并且必须删除 $R$ 上的栈结束标记。然后,$R$ 将被恢复,$L$ 将在 $L$ 的其余元素之上有 $S$ 中的 frond 元素,$B$ 将包含一个与 $S$ 减去 $p$ 中的 frond 对应的额外块。步骤 d 可以按如下方式实现:
d: **comment** apply algorithm recursively to embed the rest of S;\
$\qquad$add end-of-stack marker to R;\
$\qquad$call embedding algorithm recursively;\
$\qquad$**for** each new block (x, y) on B **do begin**\
$\qquad\quad$**if** (x $\ne$ 0) and (y $\ne$ 0) **then go to** nonplanar;\
$\qquad\quad$**if** (y $\ne$ 0) **then** move entries in block to L;\
$\qquad\quad$delete (x, y) from B;\
$\qquad$**end**;\
$\qquad$delete end-of-stack marker on R;\
$\qquad$add one block to B to represent S minus path p;
引理 12。如果步骤 d 如上所述实现,则嵌入算法正确地测试了平面性。
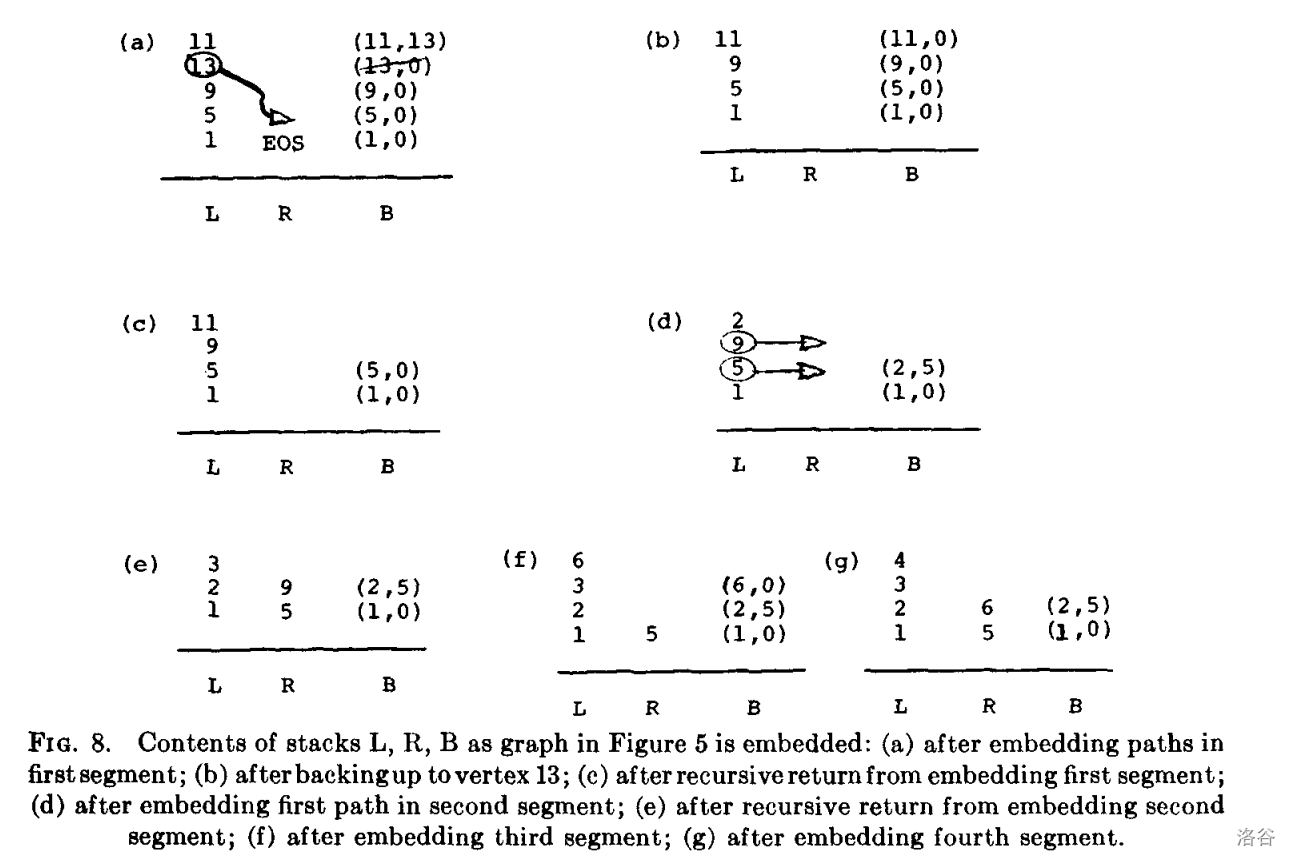
证明。这个引理来自引理 11 和 Auslander 与 Parter 的结果,即 $S$ 加 $c$ 是平面的当且仅当 $S$ 减 $p$ 可以添加到平面嵌入中。$L,R,B$ 上的旧元素不会干扰算法的递归应用,因为 $R$ 中一个栈结束标记,$L$ 上的所有元素都不大于 $f$。当递归应用完成时,$L,R,B$ 上的信息正是继续顶级算法的应用所需的信息。图 8 显示了当嵌入算法应用于图 5 中的图时,栈 $L,R,B$ 的内容。第 7 节详细给出了完整的嵌入算法。
### 7. 完整的路径嵌入算法
由于路径是在找到时嵌入的,因此嵌入算法可以与路径选择算法相结合。完整的实现如下。详细实现了涉及 $L,R$ 的步骤,使算法的运行时间很明显。


引理 13。EMBED 正确地判定了图 $G$ 的平面性。
证明。EMBED 是第 5 节和第 6 节中描述的寻路和嵌入算法的直接实现。
引理 14。EMBED 需要 $O(V+E)$ 时间来判定具有 $V$ 个顶点和 $E$ 条边的图。
证明。算法的路径寻找部分需要 $O(V+E)$ 时间,如第 5 节所述;这是一种深度优先搜索,需要进行一些额外的计算。算法的嵌入部分使用的关于路径的唯一信息是路径的端点。算法的嵌入部分由一系列栈操作组成。向栈中添加元素或从栈中删除元素需要常数时间。(任何给定的此类操作的确切步骤数可以通过检查程序来确定。)栈 $L,R,B$ 上的元素总数为 $O(V+E)$,因为路径的数量为 $E-V+1$。因此,栈计算需要 $O(V+E)$ 时间。初始化需要常数时间,因此整个算法需要 $O(V+E)$ 时间。
引理15。平面性算法需要 $O(V)$ 时间来判定具有 $V$ 个顶点的图的平面性。
证明。如果 $G$ 的边数超过 $3V-3$,则算法停止,因此计数边需要 $O(V)$ 时间。如果 $G$ 有 $O(V)$ 条边,则初始深度优先搜索需要 $O(V)$ 时间,使用 LOWPT 值对边进行排序需要 $O(V)$ 时间,路径查找/嵌入算法需要 $O(V)$ 时间。因此,总时间为 $O(V)$ 。也很容易看出,该算法需要 $O(V)$ 存储空间。
### 8. 实现与实验
不重要。
### 9. 应用与结论
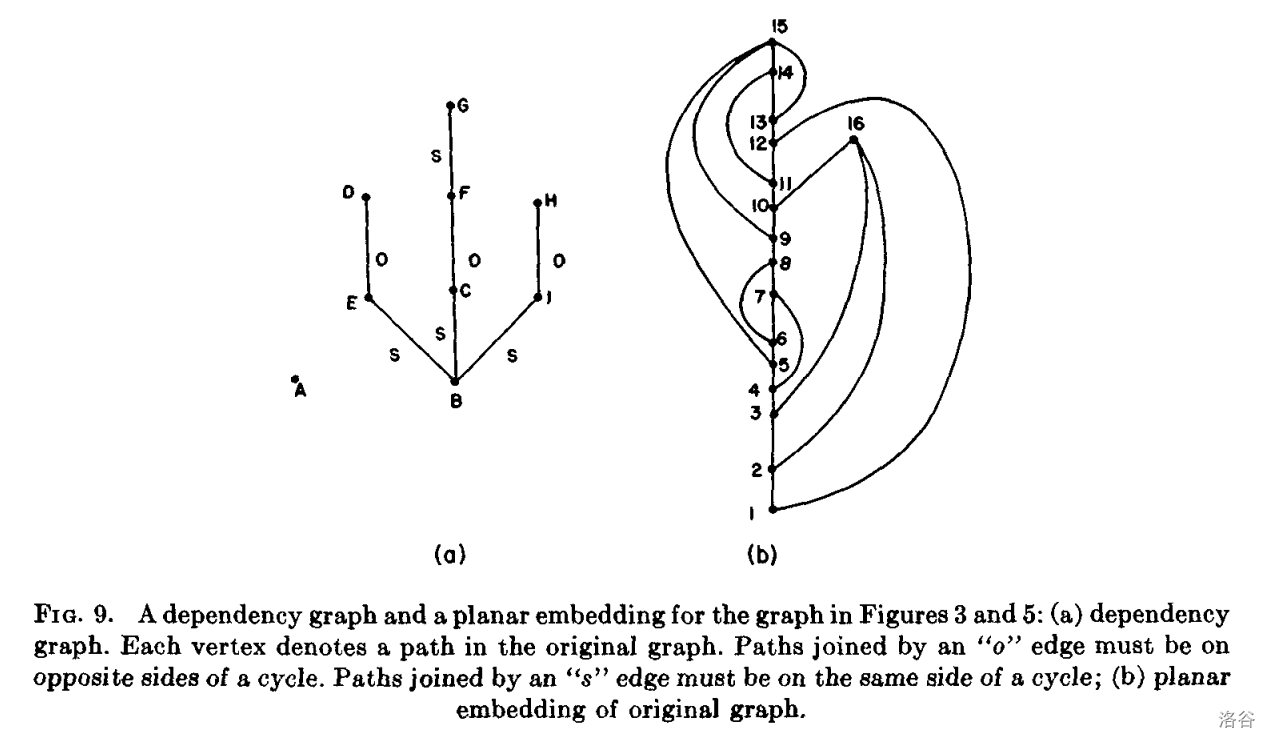
这里描述的平面性算法判定图 $G$ 的平面性,但该算法实际上并没有构造 $G$ 的平面表示。然而,该算法收集了足够的信息,使构造平面表示变得容易,并且可以稍微修改该算法以执行此步骤。实现这一点的一种方法是构建 _依赖图 / dependency graph_ $D$。依赖图的顶点将对应于 $G$ 中的路径。如果一条路径的位置决定了另一条路径,则两条路径将由一条边连接。边有两种类型,具体取决于路径必须嵌入在对应的环的同一侧还是相反侧。满足边约束的方式用两种颜色对 $D$ 的顶点进行着色对应于 $G$ 的嵌入。有关详细信息,请参见 [29]。图 9 显示了图 3 和图 5 中的依赖关系图和图的嵌入。很容易修改嵌入算法,使其构建并着色依赖图。这种修改后的算法可用于完成电子电路板布局等任务。
平面性算法可以与用于确定图的连通性的算法 [5, 6, 8] 相结合,并与 Hopcroft 的算法 [15, 17] 相结合,以判定三连通平面图的同构性,从而给出一种用于确定两个任意平面图是否同构的算法 [7, 16]。该算法需要 $O(V\log V)$ 时间和 $O(V)$ 空间。该算法有望对化学家有价值,因为大多数分子都可以表示为平面图。根据同构算法得出的分子规范形式可用于加快化学文献的搜索速度。该算法也可用于枚举各种类型的平面图。(例如,参见 Grace [43]。)
平面性算法和其他使用深度优先搜索的算法说明了该技术作为一种高效、系统的图形探索方法的价值。平面性算法也说明了精心选择的数据结构的价值。这些想法可以在解决许多其他问题的高效算法中得到应用。
\operatorname{LOWPT1}
## 支持平面图 Fáry 嵌入的小集合
### 摘要
回答了 Rosenstiehl 与 Tarjan 的问题,我们证明了任意 $n$ 个顶点的平面图都有一个 $2n-4$ 乘 $n-2$ 网格中的 Fáry 嵌入(即,直线嵌入)并且提供了一个 $O(n)$ 空间、$O(n\log n)$ 时间的算法来产生这样的嵌入。另一方面,我们证明了,对于任意能支持每个大小 $n$ 的平面图的 Fáry 嵌入的集合 $F$,大小至少为 $n+(1-o(1))\sqrt n$,解决了 Mohar 问题。
### 1. 引言
I. Fáry [F] 的定理表明:所有平面图都存在点在平面上、边是平面上直线的嵌入。这类嵌入称作 Fáry 嵌入。从 Tutte 1963 年的论文开始,已经有了许多构造 Fáry 嵌入的算法([T], [CYN], [Rd])。现在的所有寻找平面图 Fáry 嵌入的算法都有一些缺陷。这些缺陷是(1)这些算法需要与图大小相关的高精度实数计算与(2)顶点趋向于聚在一起,顶点间最小距离与最大距离的比值非常小。这意味着:(1)对于一个中等大小的图,都不可能运行这个算法且(2)即使可以,也不可能在终端屏幕上展示得到的结果。
实际上,确定是否存在固定的 $k$,使得任何一个大小为 $n$ 的平面图可以 Fáry 嵌入到边界长度被 $n^k$ 限定的网格中是一个仍未解决的问题 [RT]。类似这样关于平面图能被多紧凑地嵌入到网格中的问题,与 VLSI 布局设计问题相关([L], [U], [V])。定理 1 对这个问题给出了一个肯定回答,其证明给出了一个构造这类嵌入的算法。
定理 1。任何 $n$ 个点的平面图都有 $2n-4$ 乘 $n-2$ 网格上的 Fáry 嵌入。
可以证明,一个 $\dfrac n3$ 个三角形组成的交错序列在网格上的 Fáry 嵌入至少需要大小为 $\left(\dfrac23n-1\right)\times\left(\dfrac23n-1\right)$ 的网格。
因为 Hopcroft-Tarjan 平面图判定算法 [HT] 给出了一个平面图的拓扑嵌入,我们将假设我们考察的所有图都已经通过了检测,并且具有一个这样的嵌入。一个 _极大_ 平面图是不能加入任何不破坏其平面性的附加边的图。这样的图被称为 _三角化图_ 因为图中所有的面都是三角形。因为每个平面图都可以通过加入附加的(无用的)边进行三角化,对所有极大平面图证明定理 1 就足够了。
我们通过提供一个输入任意极大平面图、任意三角面,输出以给定三角形为外边界的嵌入的算法在 Section 3 中证明定理 1。我们的证明基于被称为 _平面图的典范表示_ 的通用构造(Section 2),该表示提供了一个合适的顶点顺序,使得我们可以归纳地将前 $k$ 个顶点的导出子图嵌入网格中,然后通过以受控的方式移动嵌入中的一些顶点,我们可以添加下一个顶点,并且仍然拥有 Fáry 嵌入。表面上开,这个算法至少是平方时间复杂度的。将算法加速到 $O(n\log n)$ 的方法是:不实际进行每次嵌入,而是将所需的所有信息存储在一个排列里,我们可以在 $O(n\log n)$ 时间内构造这个排列。然后我们会进行 $O(n)$ 次关于排列的询问:对于下标 $i,j$,有多少个排列中的 $k$ 满足 $i\le k\le j,p_k<p_i$。这些询问的答案将被用来找到嵌入顶点的坐标。这些询问可以被表示为对 $2n$ 个点的矩形范围查询,这些点是从排列中导出的,并使用 Chazelle [C] 的数据结构,该数据结构使用线性空间,$O(n\log n)$ 预处理时间,每个查询都可以在时间 $O(\log n)$ 内执行。
平面图的典范表示是一个有用的证明带有便于归纳论证的特殊的几何性质的 Fáry 嵌入存在性的工具。命题 1 2 3 是几个例子。
命题 1。给定极大平面图 $G$ 与一个面 $uvw$,存在顶点的标号方式,$v_1=u,v_2=v,v_3,\dots,v_n=w$ 与 Fáry 嵌入 $f$ 使得对于 $k=4,\dots,n$ 有 $\{f(v_1),f(v_2),f(v_3),\dots,f(v_k)\}$ 的凸包与 $\{f(v_1),f(v_2),f(v_k)\}$ 的凸包相同。
命题 2。给定极大平面图 $G$ 与一个面 $uvw$,存在顶点的标号方式,$v_1=u,v_2=v,v_3,\dots,v_n=w$ 与一个 Fáry 嵌入 $f$ 使得对于 $k=4,\dots,n$ 有 $\{f(v_1),f(v_2),f(v_3),\dots,f(v_k)\}$ 的凸包与 $\{f(v_{k-2}),f(v_{k-1}),f(v_k)\}$ 的凸包相同。
命题 3。给定极大平面图 $G$ 与一个面 $uvw$,存在顶点的标号方式,$v_1=u,v_2=v,v_3,\dots,v_n=w$ 与一个 Fáry 嵌入 $f$ 使得对于 $k=4,\dots,n$ 有 $\{f(v_1),f(v_2),f(v_3),\dots,f(v_k)\}$ 的凸包的边界是一个 $G$ 中的环,且 $f(v_{k+1})$ 不包含在 $\{f(v_1),f(v_2),f(v_3),\dots,f(v_k)\}$ 的凸包中。
定理 1 给出了可支持大小为 $n$ 的平面图的最小网格大小的渐进紧边界。即使网格是自然的嵌入图的集合,取消网格的限制,寻找支持所有大小为 $n$ 的平面图的集合的大小的界也是有意义的。去年,Bojan Mohar [M] 问是否存在平面上 $n$ 个点的支持所有 $n$ 个顶点的平面图的集合(一个集合 $F$ _支持_ 一个简单平面图,如果存在单射 $f:V(G)\to F$ 使得如果 $[a,b],[c,d]$ 是 $G$ 的边,线段 $[f(a),f(b)]$ 与 $[f(c),f(d)]$ 开不相交)。对于一个平面图的集合,$F$ 被称为 _通用的_,如果其支持集合中的所有图。因此由 Fáry 定理,$\mathbb R^2$ 关于所有平面图是通用的,由定理 1,$n-2$ 乘 $2n-4$ 网格关于所有 $n$ 个顶点的平面图是通用的。Mohar 问是否存在一个大小为 $n$ 的集合关于 $n$ 个点的所有平面图通用。
我们在 Section 5 中对此问题给出否定回答,我们证明了:
定理 2。如果 $F$ 关于所有 $n$ 个顶点的平面图通用,那么 $|F|>n+(1-o(1))\sqrt n$。
### 2. 平面图的典范表示
本节的目的是描述构造平面图的典范方法,这将是我们在本文其余部分研究的基本工具,并且还提供了 Fáry 定理推广(命题 1.2 和 3)的简单证明。
下面的简单观察对我们的目标至关重要。
引理。设 $G$ 是一个嵌入到平面中的简单平面图,$u=u_1,u_2,\dots,u_k=v$ 为 $G$ 的环。则存在环上不同于 $u,v$ 的顶点 $w'$(相应的,$w''$)不与任何内弦(相应的,外弦)相邻。
证明。如果一个环没有任何内弦(相应的,外弦),那么证明完成。否则,设 $(u_i,u_j),j>i+1$ 为 $j-i$ 最小的内弦(外弦)。则由极小性,$u_{i+1}$ 不与任何环 $u_i,u_{i+1},\dots,u_j$ 上的内弦相邻。由平面性,这个点不能与原始环的任何内弦(外弦)相邻。$\quad\Box
弦是环中连接两个不相邻顶点的边。
顶点与边相邻的意思是顶点为边的一个端点。
现在我们可以证明如下引理
平面图的典范表示引理。设 G 是嵌入到平面中的极大平面图,其外边界为三角形 u,v,w。则存在顶点的标号方式 v_1=u,v_2=v,v_3,\dots,v_n=w 对于任意 4\le n\le n 满足下面的要求。
(i) v_1,v_2,\dots,v_{k-1} 的导出子图 G_{k-1}\subseteq G 是 2-连通图,其外部面的边界是包含边 uv 的环 C_{k-1}。
\begin{aligned}M(k,v_i)&=\{j|j\le n,j\text{ does not precede }i\text{ in }\pi_k\}\\&=\{j|i\le j\le n,j\text{ does not precede }i\text{ in }\pi_k\}\end{aligned}
[C] B. CHAZELLE. Slimming down searching structures functional approach to algorithm design, in Proceedings of the Twenty Sixth Annual Symposium on the Foundations of Computer Science. 1985, pp. 165-174.
[CYN] N. CHIRA, T. YAMANOUCHI, AND T. NISHIZEKI. Linear algorithms for convex drawings of planar graphs, in Progress in graph theory, 1982, pp. 153-173.
[Dea] P. DUCHET, Y. HAMIDOUNE, M. LAS VERGNAS, AND H. MEYNIEL. Representing a planar graph by vertical lines joining different intervals. Discrete Math., 46 (1983), pp. 319-321.
[F] I. FÁRY. On straight line representing of planar graphs. Acta. Sci. Math. (Szeged), 11 (1948). pp. 229-233.
[dF] H. DE FHAYSSEIXl. Drawing planar and non-planar graphs from the half-edge code, (to appear).
[dFR1] H. DE FHAYSSEIXl AND P. ROSENSTIEHL. Structures combinatoires pour traces automatiques do resaux, in Proceedings of the Third European Conference on CAD CAM and Computer Graphics, 1984, pp. 332-337.
[dFR2] H. DE FHAYSSEIXl AND P. ROSENSTIEHL. L'algorithme Gauchedroite pour le plongement des graphes dans le plan, (to appear).
[G] D.H. GREENE, Efficient coding and drawing of planar graphs, Xerox Palo Alto Research Center. Palo Alto, CA.
[Gr] G. GRÜNBAUM, Convex Polytopes, John Wiley.
[HT] J. HOPCROFT AND R. TARJAN. Efficient planarity testing, J. Comput. Mach., 21 (1974), pp. 549-568.
[L] F. T. LEIGHTON, Complexity Issues in VLSI, The MIT Press.
[M] B. MOHAR, private communication.
[OvW] R. H. J. M. OTTEN AND J. G. Van WIJK. Graph representation in interactive layout design, in Proceedings of the IEEE International Symposium on Circuits and Systems, 1978, pp. 914-918.
[R] P. ROSENSTIEHL. Embedding in the plane with orientation constraints. Ann. N. Y. Acad. Sci. (to appear).
[Rd] R. C. READ. A new method for drawing a planar graph given the cyclic order of the edges at each vertex. Congresus Numerantium. 56. pp. 31-44.
[RT] P. ROSENSTIEHL. AND R. E. TARJAN. Rectilinear planar layouts and bipolar orientations of planar graphs. Disc. Comp. Geom., 1 (1986), pp. 343-353.
[TT] R. TOMMASIA AND I. G. TOLLIS. A unified approach to visibility representations of planar graphs. Disc. Comp. Geom., 1 (1986), pp. 321-341.
[T] W. T. TUTTE. How to draw a graph. Proc. London Math. Soc., 13 (1963). pp. 743-768.
[U] J. D. ULLMAN, Computational Aspects of VLSI, Computer Science Press.
[V] L. G. VALIANT. Universality considerations in VLSI circuits. IEEE Trans. on Computers. C-30. pp. 135-140.
[W] D. R. WOODS. Drawing planar graphs. in Report N. STAN-CS-82-942, Computer Science Department. Stanford University, CA. 1981.