快速沃尔什变换 FWT
MarchKid_Joe
·
·
个人记录
快速沃尔什变换
FWT
快速沃尔什变换(\operatorname{FWT})不同于快速傅里叶变换(\operatorname{FFT})和快速数论变换(\operatorname{NTT})。
普通卷积类型的多项式:F=A*B。一般用 \operatorname{FFT} 和 \operatorname{NTT} 解决。
F_x=\displaystyle\sum_{i+j=x}A_i\times B_j
特殊卷积类型的多项式:F=A*B。可以用 \operatorname{FWT} 解决,其中 \oplus 为二进制运算。
F_x=\displaystyle\sum_{i\oplus j=x}A_i\times B_j
定义
$F_x$:多项式 $F$ 的第 $x$ 项的**系数**。特殊的:$F_0,F_1$ 表示左半多项式和右半多项式,具体含义文章会解释。
$F+G$:多项式 $F$ 和 $G$ 对应系数相加。
$i\supset j$:二进制状态下 $i$ 中的 $1$ 的位置是 $j$ 的 $1$ 的位置的**子集**。
$\operatorname{popcount}(x)$:$x$ 在二进制表示下 $1$ 的个数。
$\text{or}$:或运算。
$\text{and}$:与运算。
$\text{xor}$:异或运算。
$\text{xnor}$:同或运算。
$n$:经典多项式,保证 $n=2^k-1$。
# 或运算
## 卷积公式
$$
F_x=\displaystyle\sum_{(i \text{ or }j)=x}A_i\times B_j
$$
## 正变换
定义多项式 $F$ 的或运算的**沃尔什正变换**为:
$$
\begin{aligned}
\operatorname{FWT}(F)
_i
&=\displaystyle\sum_{j=0}^{n} F_j[(i\text{ or }j)=i]\\
&=\displaystyle\sum_{j\supset i}^{n} F_j
\end{aligned}
$$
考虑改如何变换。
采用**分治**算法,时间复杂度 $O(n\log n)$。
设多项式为 $F$ 共 $2^k$ 项,将**项数**拆为平均分为两部分,左右部分的区间各自含有 $2^{k-1}$ 项,左区间记作 $F_0$,右区间记作 $F_1$,这里的 $F_0,F_1$ 指的是左半和右半多项式。
---
PS:对于**或运算**来说右半区间包含左半区间的贡献,比如一段区间(如 $[4,7]$),从中间分离两个区间,左半部分($[4,5]$)与右半部分($[6,7]$)一一对应,从二进制 $1$ 的位置角度看 $4\supset6,5\supset7$。如图:
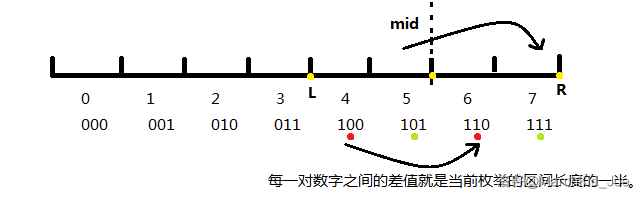
---
然后我们可以得到:
$$
F_0\to F'_0,F_0+F_1\to F'_1
$$
从二进制的角度理解右半区间包含左半区间的贡献的话,貌似 $1$ 更多一点:
$$
\begin{aligned}
0=0{\text{ or }}0\\
1=0{\text{ or }}1\\
1=1{\text{ or }}0\\
1=1{\text{ or }}1\\
\end{aligned}
$$
感性理解:$1$ 的贡献一定要包含 $0$ 的贡献,所以转移更新的式子:
$$
\operatorname{FWT}(F)=\operatorname{replace}(\operatorname{FWT}(F_0),\operatorname{FWT}(F_0+F_1))
$$
$\operatorname{replace}$:对应位置的权值被替换为相应的权值,反映到代码上就是:
$$
F_0=F_0;F_1=F_0+F_1;
$$
---
PS:或者是网上的大多数版本:
$$
\operatorname{FWT}(F)=
\begin{cases}
\operatorname{merge}(\operatorname{FWT}(F_0),\operatorname{FWT}(F_0+F_1))&n\gt1\\
F&n=1\\
\end{cases}
$$
个人觉得 $\operatorname{replace}$ 好理解,有人解释的 $\operatorname{merge}$ 含义是像字符串一样拼起来(举例 $\operatorname{merge}(114,514)=114514$)。个人感觉没有任何关系,应该指的是**合并贡献**的意思吧。此篇文章均采用 $\operatorname{replace}$。
---
还有一张图便于读者理解(图片来源于[巨佬博客](https://www.cnblogs.com/wyb-sen/p/15779952.html)),能很好地描述 $\operatorname{FWT}$:
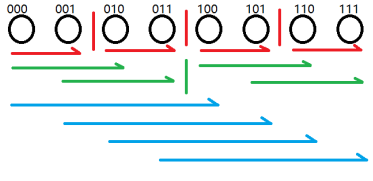
一种颜色代表当前这一层的处理方式,每个箭头起点的贡献累加到终点的贡献,恰好是**子集**和。
## 卷积
卷积时间复杂度 $O(n)$,处理完了 $\operatorname{FWT}(A),\operatorname{FWT}(B)$。现在要证明:
$$
\operatorname{FWT}(A)*\operatorname{FWT}(B)=\operatorname{FWT}(F)
$$
那现在证明任意一项成立即可:
$$
\begin{aligned}
\operatorname{FWT}(F)_k
&=\displaystyle\sum_{s\supset k}^{n} F_s\\
&=\displaystyle\sum_{s\supset k}^{n}\displaystyle\sum_{(i\text{ or }j)=s} A_i\times B_j\\
&=\displaystyle\sum_{(i\text{ or }j)\supset k}^{n} A_i\times B_j\\
&=\displaystyle\sum_{i\supset k}^{n} A_i\times \displaystyle\sum_{j\supset k}^{n}B_j\\
&=\operatorname{FWT} (A)_k*\operatorname{FWT} (B)_k
\end{aligned}
$$
## 逆变换
多项式 $F$ 的**沃尔什逆变换**为点值变换为系数。
简单的理解为:既然正变换 $\operatorname{FWT}$ 时 $F_1$ 加上了 $F_0$ 的贡献,逆变换减回去就行了:
$$
\operatorname{IFWT}(F)=\operatorname{replace}(\operatorname{IFWT}(F_0),\operatorname{IFWT}(F_1-F_0))
$$
经过了正变换,已经求出来了 $\operatorname{FWT}(A)$,所以也就已知了 $\operatorname{FWT}(A)_0,\operatorname{FWT}(A)_1$。
首先区分:
$\operatorname{FWT}(A)_0$ :多项式 $\operatorname{FWT}(A)$ 的左半区间。
$\operatorname{FWT}(A_0)$ :正变换多项式左半区间 $A_0$ 得到的多项式。
$\operatorname{FWT}(A)_1$ :多项式 $\operatorname{FWT}(A)$ 的右半区间。
$\operatorname{FWT}(A_1)$ :正变换多项式右半区间 $A_0$ 得到的多项式。
证明:
$$
\begin{aligned}
\operatorname{FWT}(A)_0
&=\operatorname{FWT}(A_0)\\
\operatorname{FWT}(A_0)
&=\operatorname{FWT}(A)_0\\\\
\operatorname{FWT}(A)_1
&=\operatorname{FWT}(A_0)+\operatorname{FWT}(A_1)\\
\operatorname{FWT}(A_1)
&=\operatorname{FWT}(A)_1-\operatorname{FWT}(A_0)\\
&=\operatorname{FWT}(A)_1-\operatorname{FWT}(A)_0\\\\
A_0
&=\operatorname{IFWT}(\operatorname{FWT}(A_0))\\
&=\operatorname{IFWT}(\operatorname{FWT}(A)_0)\\\\
A_1
&=\operatorname{IFWT}(\operatorname{FWT}(A_1))\\
&=\operatorname{IFWT}(\operatorname{FWT}(A)_1-\operatorname{FWT}(A)_0)\\\\
\end{aligned}
$$
## Code
```cpp
void FWT_OR(int *A)
{
for (int i = 1; i < length; i <<= 1)
for (int j = 0; j < length; j += (i << 1))
for (int k = j; k < j + i; k++)
{
A[k] = A[k];
A[k + i] = A[k + i] + A[k];
}
}
void IFWT_OR(int *A)
{
for (int i = 1; i < length; i <<= 1)
for (int j = 0; j < length; j += (i << 1))
for (int k = j; k < j + i; k++)
{
A[k] = A[k];
A[k + i] = A[k + i] - A[k];
}
}
```
或者直接写成一个函数:
```cpp
void FWT_OR(int *A, int opt) /*opt={-1,+1}*/
{
for (int i = 1; i < length; i <<= 1)
for (int j = 0; j < length; j += (i << 1))
for (int k = j; k < j + i; k++)
A[k + i] = A[k + i] + opt * A[k];
}
```
# 与运算
## 卷积公式
$$
F(x)=\displaystyle\sum_{(i \text{ and }j)=x}A(i)\times B(j)
$$
## 正变换
定义多项式 $F$ 的与运算的**沃尔什正变换**为:
$$
\begin{aligned}
\operatorname{FWT}(F)_i
&=\displaystyle\sum_{j=0}^{n} F_j[(i\text{ and }j)=i]\\
&=\displaystyle\sum_{i\supset j}^{n} F_j
\end{aligned}
$$
变换类比或运算,还是分治,时间复杂度 $O(n\log n)$。
设多项式为 $F$ 共 $2^k$ 项,将**项数**拆为平均分为两部分,左右部分的区间各自含有 $2^{k-1}$ 个,左区间记作 $F_0$,右区间记作 $F_1$。
然后我们可以得到:
$$
F_0+F_1\to F'_0,F_1\to F'_1
$$
从二进制角度理解:
$$
\begin{aligned}
0=0{\text{ and }}0\\
0=0{\text{ and }}1\\
0=1{\text{ and }}0\\
1=1{\text{ and }}1\\
\end{aligned}
$$
所以恰好和或运算相反,由此得到转移更新的式子:
$$
\operatorname{FWT}(F)=\operatorname{replace}(\operatorname{FWT}(F_0+F_1),\operatorname{FWT}(F_1))
$$
图,~~把箭头反过来就好啦~~:
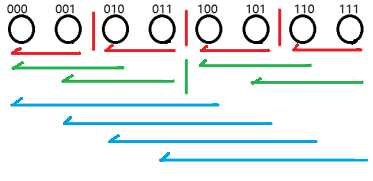
## 卷积
卷积时间复杂度 $O(n)$,处理完了 $\operatorname{FWT}(A),\operatorname{FWT}(B)$。现在要证明:
$$
\operatorname{FWT}(A)*\operatorname{FWT}(B)=\operatorname{FWT}(F)
$$
那现在证明任意一项,其实和或运算基本一样:
$$
\begin{aligned}
\operatorname{FWT}(F)_k
&=\displaystyle\sum_{k\supset s}^{n}F_s\\
&=\displaystyle\sum_{k\supset s}^{n}\displaystyle\sum_{(i\text{ and }j)=s}A_i\times B_j\\
&=\displaystyle\sum_{k\supset(i\text{ and }j)}^{n}A_i\times B_j\\
&=\displaystyle\sum_{k\supset i}^{n}A_i\times \displaystyle\sum_{k\supset j}^{n}B_j\\
&=\operatorname{FWT}(A)_k*\operatorname{FWT}(B)_k
\end{aligned}
$$
## 逆变换
多项式 $F$ 的**沃尔什逆变换**为点值变换为系数。
简单的理解为:既然正变换 $\operatorname{FWT}$ 时 $F_0$ 加上了 $F_1$ 的贡献,逆变换减回去就行了:
$$
\operatorname{IFWT}(F)=\operatorname{replace}(\operatorname{IFWT}(F_0-F_1),\operatorname{IFWT}(F_1))
$$
证明:
$$
\begin{aligned}
\operatorname{FWT}(A)_1
&=\operatorname{FWT}(A_1)\\
\operatorname{FWT}(A_1)
&=\operatorname{FWT}(A)_1\\\\
\operatorname{FWT}(A)_0
&=\operatorname{FWT}(A_0)+\operatorname{FWT}(A_1)\\
\operatorname{FWT}(A_0)
&=\operatorname{FWT}(A)_0-\operatorname{FWT}(A_1)\\
&=\operatorname{FWT}(A)_0-\operatorname{FWT}(A)_1\\\\
A_1
&=\operatorname{IFWT}(\operatorname{FWT}(A_1))\\
&=\operatorname{IFWT}(\operatorname{FWT}(A)_1)\\\\
A_0
&=\operatorname{IFWT}(\operatorname{FWT}(A_0))\\
&=\operatorname{IFWT}(\operatorname{FWT}(A)_0-\operatorname{FWT}(A)_1)\\\\
\end{aligned}
$$
## Code
```cpp
void FWT_AND(int *A)
{
for (int i = 1; i < length; i <<= 1)
for (int j = 0; j < length; j += (i << 1))
for (int k = j; k < j + i; k++)
{
A[k + i] = A[k + i];
A[k] = A[k] + A[k + i];
}
}
void IFWT_AND(int *A)
{
for (int i = 1; i < length; i <<= 1)
for (int j = 0; j < length; j += (i << 1))
for (int k = j; k < j + i; k++)
{
A[k + i] = A[k + i];
A[k] = A[k] - A[k + i];
}
}
```
直接写成一个函数:
```cpp
void FWT_AND(int *A, int opt) /*opt={-1,+1}*/
{
for (int i = 1; i < length; i <<= 1)
for (int j = 0; j < length; j += (i << 1))
for (int k = j; k < j + i; k++)
A[k] = A[k] + opt * A[k + i];
}
```
# 异或运算
PS:网络上都说前两个基本没用,异或考的最多。为了方便,以下的所有 $\operatorname{popcount}$ 简记为 $\operatorname{pop}$。
## 卷积公式
$$
F(x)=\displaystyle\sum_{(i\text{ xor }j)=x}A(i)*B(j)
$$
## 正变换
定义多项式 $F$ 的异或运算的**沃尔什正变换**为:
$$
\begin{aligned}
\operatorname{FWT}(F)_i
&=\displaystyle\sum_{j=0}^{n}F_j[(i\text{ xor }j)=i]\\
&=\displaystyle\sum_{j=0}^{n}(-1)^{\operatorname{pop}(i\text{ and }j)}F_j
\end{aligned}
$$
转移更新的式子:
$$
\operatorname{FWT}(F)=\operatorname{replace}(\operatorname{FWT}(F_0+F_1),\operatorname{FWT}(F_0-F_1))
$$
## 卷积
卷积时间复杂度 $O(n)$,处理完了 $\operatorname{FWT}A,\operatorname{FWT}B$。现在要证明:
$$
\operatorname{FWT}(A)*\operatorname{FWT}(B)=\operatorname{FWT}(F)
$$
还是证明任意一项,但是首先需要一个定理:
$$
(\operatorname{pop}(i\text{ and }k)\text{ and }1)\text{ xor }(\operatorname{pop}(j\text{ and }k)\text{ and }1)=\operatorname{pop}((i\text{ xor }j)\text{ and }k)\text{ and }1
$$
用文字表达这个式子就是:$k$ **按位与** $i,j$ **按位异或**的值的**奇偶性**与 $k$ 分别**按位与** $i,j$ 的值的**按位异或**的值的**奇偶性**相同。
$$
\begin{aligned}
\operatorname{FWT} (F)_k
&=\displaystyle\sum_{s=0}^{n} (-1)^{\operatorname{pop}(k\text{ and } s)}F_s\\
&=\displaystyle\sum_{s=0}^{n}(-1)^{\operatorname{pop}(k\text{ and } s)}\displaystyle\sum_{(i\text{ xor }j)=s}^{n}A_i\times B_j\\
&=\displaystyle\sum_{i=0}^{n}\displaystyle\sum_{j=0}^{n} (-1)^{\operatorname{pop}(k\text{ and } (i\text{ xor }j))}A_i\times B_j\\
&=\displaystyle\sum_{i=0}^{n}\displaystyle\sum_{j=0}^{n} (-1)^{(\operatorname{pop}(k\text{ and } i))\text{ xor }(\operatorname{pop}(k\text{ and }j))}A_i\times B_j\\
\end{aligned}
$$
发现 $(-1)^k$ 的取值只与指数 $k$ 的奇偶性有关。显然对于异或运算满足:
奇数异或奇数结果:偶数。
偶数异或偶数结果:偶数。
偶数异或奇数结果:奇数。
奇数异或偶数结果:奇数。
所以原式中作为 $-1$ 指数的 $\operatorname{pop}(k\text{ and }i)\text{ xor }\operatorname{pop}(k\text{ and }j)$ 与 $(\operatorname{pop}(i\text{ and }k)\text{ and }1)\text{ xor }(\operatorname{pop}(j\text{ and }k)\text{ and }1)$ 是等价的。
此时这个式子只有四种情况,又发现:
$$
\begin{aligned}
(-1)^{1 \text{ xor } 1}&=(-1)^0=(-1)^{1+1}=(-1)^2=+1\\
(-1)^{1 \text{ xor } 0}&=(-1)^1=(-1)^{1+0}=(-1)^1=-1\\
(-1)^{0 \text{ xor } 1}&=(-1)^1=(-1)^{0+1}=(-1)^1=-1\\
(-1)^{0 \text{ xor } 0}&=(-1)^0=(-1)^{0+0}=(-1)^0=+1\\
\end{aligned}
$$
发现 $(\operatorname{pop}(i\text{ and }k)\text{ and }1)\text{ xor }(\operatorname{pop}(j\text{ and }k)\text{ and }1)$ 与 $(\operatorname{pop}(i\text{ and }k)\text{ and }1)+(\operatorname{pop}(j\text{ and }k)\text{ and }1)$ 也是等价的,也就是此处 $\text{xor}$ 和 $+$ 等价。替换之后,此时我们继续推式子:
$$
\begin{aligned}
\operatorname{FWT}(F)_k
&=\displaystyle\sum_{i=0}^{n}\displaystyle\sum_{j=0}^{n}(-1)^{(\operatorname{pop}(k\text{ and }i))\text{ xor }(\operatorname{pop}(k\text{ and }j))}A_i\times B_j\\
&=\displaystyle\sum_{i=0}^{n}\displaystyle\sum_{j=0}^{n}(-1)^{(\operatorname{pop}(i\text{ and }k)\text{ and }1)+(\operatorname{pop}(j\text{ and }k)\text{ and }1)}A(i)\times B(j)\\
&=\displaystyle\sum_{i=0}^{n}(-1)^{\operatorname{pop}(i\text{ and }k)\text{ and }1}A(i)\times\displaystyle\sum_{j=0}^{n} (-1)^{\operatorname{pop}(j\text{ and }k)\text{ and }1}B(j)\\
&=\displaystyle\sum_{i=0}^{n}(-1)^{\operatorname{pop}(i\text{ and }k)}A(i)\times\displaystyle\sum_{j=0}^{n} (-1)^{\operatorname{pop}(j\text{ and }k)}B(j)\\
&=\operatorname{FWT}(A)_k*\operatorname{FWT}(B)_k
\end{aligned}
$$
## 逆变换
多项式 $F$ 的**沃尔什逆变换**为点值变换为系数。
似乎不太能感性理解。
$$
\operatorname{IFWT}(F)=\operatorname{replace}(\operatorname{IFWT}(\frac{F_0+F_1}{2}),\operatorname{IFWT}(\frac{F_0-F_1}{2}))
$$
证明:
$$
\begin{aligned}
\operatorname{FWT}(A)_0
&=\operatorname{FWT}(A_0)+\operatorname{FWT}(A_1)\\
\operatorname{FWT}(A_0)
&=\operatorname{FWT}(A)_0-\operatorname{FWT}(A_1)\\\\
\operatorname{FWT}(A)_1
&=\operatorname{FWT}(A_0)-\operatorname{FWT}(A_1)\\
\operatorname{FWT}(A_1)
&=\operatorname{FWT}(A_0)-\operatorname{FWT}(A)_1\\\\
\operatorname{FWT}(A_0)
&=\operatorname{FWT}(A)_0-\operatorname{FWT}(A_0)+\operatorname{FWT}(A)_1\\
&=\frac{\operatorname{FWT}(A)_0+\operatorname{FWT}(A)_1}{2}\\\\
\operatorname{FWT}(A_1)
&=\operatorname{FWT}(A)_0-\operatorname{FWT}(A_1)-\operatorname{FWT}(A)_1\\
&=\frac{\operatorname{FWT}(A)_0-\operatorname{FWT}(A)_1}{2}\\\\
A_0
&=\operatorname{IFWT}(\operatorname{FWT}(A_0))\\
&=\operatorname{IFWT}(\frac{\operatorname{FWT}(A)_0+\operatorname{FWT}(A)_1}{2})\\\\
A_1
&=\operatorname{IFWT}(\operatorname{FWT}(A_1))\\
&=\operatorname{IFWT}(\frac{\operatorname{FWT}(A)_0-\operatorname{FWT}(A)_1}{2})\\\\
\end{aligned}
$$
## Code
```cpp
void FWT_XOR(int *A, int opt) /*opt={-1,+1}*/
{
for (int i = 1; i < length; i <<= 1)
{
for (int j = 0; j < length; j += (i << 1))
{
for (int k = j; k < j + i; k++)
{
int x = A[k], y = A[k + i];
A[k] = (x + y) / (opt == -1 ? 2 : 1);
A[k + i] = (x - y) / (opt == -1 ? 2 : 1);
}
}
}
}
```
# Summary
## 卷积
$$
\begin{aligned}
\text{or}&:F_x=\displaystyle\sum_{(i \text{ or }j)=x}A_i\times B_j\\
\text{and}&:F_x=\displaystyle\sum_{(i \text{ and }j)=x}A_i\times B_j\\
\text{xor}&:F_x=\displaystyle\sum_{(i \text{ xor }j)=x}A_i\times B_j\\
\end{aligned}
$$
## 正变换定义
$$
\begin{aligned}
\text{or}&:\operatorname{FWT}(F)
_i=\displaystyle\sum_{j\supset i}^{n} F_j\\
\text{and}&:\operatorname{FWT}(F)
_i=\displaystyle\sum_{i\supset j}^{n} F_j\\
\text{xor}&:\operatorname{FWT}(F)_i=\displaystyle\sum_{j=0}^{n} (-1)^{\operatorname{popcount}(i\text{ and } j)}F_j\\
\end{aligned}
$$
## 正变换
$$
\begin{aligned}
\text{or}&:\operatorname{FWT}(F)=\operatorname{replace}(\operatorname{FWT}(F_0),\operatorname{FWT}(F_0+F_1))\\
\text{and}&:\operatorname{FWT}(F)=\operatorname{replace}(\operatorname{FWT}(F_0+F_1),\operatorname{FWT}(F_1))\\
\text{xor}&:\operatorname{FWT}(F)=\operatorname{replace}(\operatorname{FWT}(F_0+F_1),\operatorname{FWT}(F_0-F_1))\\
\text{xnor}&:\operatorname{FWT}(F)=\operatorname{replace}(\operatorname{FWT}(F_1-F_0),\operatorname{FWT}(F_1+F_0))\\
\end{aligned}
$$
## 逆变换
$$
\begin{aligned}
\text{or}&:\operatorname{FWT}(F)=\operatorname{replace}(\operatorname{FWT}(F_0),\operatorname{FWT}(F_1-F_0))\\
\text{and}&:\operatorname{FWT}(F)=\operatorname{replace}(\operatorname{FWT}(F_0-F_1),\operatorname{FWT}(F_1))\\
\text{xor}&:\operatorname{FWT}(F)=\operatorname{replace}(\operatorname{FWT}(\frac{F_0+F_1}{2}),\operatorname{FWT}(\frac{F_0-F_1}{2}))\\
\text{xnor}&:\operatorname{FWT}(F)=\operatorname{replace}(\operatorname{FWT}(\frac{F_1-F_0}{2}),\operatorname{FWT}(\frac{F_1+F_0}{2}))\\
\end{aligned}
$$
# 例题
## [CF662C:Binary Table](https://www.luogu.com.cn/problem/CF662C)
### 题意
给定 ${n}\times{m}$ 的表格,每行每列均可 $01$ 反转任意次。求反转若干次后表格最少会剩余多少个 $1$。
### 思路
对每列的 $01$ 串进行状态压缩,每列的状态最大为 $2^n$,记为集合 $\{S\}$。
对每行的反转情况进行状态压缩 $X$,可知最多有 $2^n$ 种状态。
对于行的反转状态 $X$,第 $i$ 列在按照状态 $X$ 反转后的状态为 $X\text{ xor }S_i$;因为每列也可以反转,所以第 $i$ 列再自身反转后状态为 $(2^{n}-1)\text{ xor }X\text{ xor }S_i$。两种情况取 $1$ 个数最少的。
得出时间复杂度为 $O(2^nm)$ 的状态转移方程:
$$
\displaystyle\min_{X=0}^{2^n-1}\sum_{i=1}^{m}\min\{\operatorname{popcount(X\text{ xor }S_i),popcount((2^{n}-1)\text{ xor }X\text{ xor }S_i)}\}
$$
```cpp
for (int X = 0, limit = (1 << n) - 1; X <= limit; X++)
{
int sum = 0;
for (int i = 1; i <= m; i++)
sum += min(__popcount(X ^ S[i]), __popcount(limit ^ X ^ S[i]));
ans = min(sum, ans);
}
```
考虑更换枚举方式,枚举状态为 $Y$ 的列有多少个,记 $F_Y$ 为状态为 $Y$ 的列的数量,$G_Y$ 为 $Y$ 二进制反转或者不反转两种情况下 $1$ 的最少数量,即:
$$
\begin{aligned}
F_Y&=\sum_{i=1}^{m}[S_i=Y]\\
G_Y&=\min\{\operatorname{popcount(Y),popcount((2^{n}-1)\text{ xor }Y)}\}
\end{aligned}
$$
得到时间复杂度为 $O(2^{2n})$ 的状态转移方程:
$$
\displaystyle\min_{X=0}^{2^n-1}\sum_{Y=0}^{2^n-1}{F_Y}\times{G_{X\text{ xor }Y}}
$$
```cpp
for (int i = 0; i < (1 << n); i++)
G[i] = min(__popcount(i), n - __popcount(i));
for (int X = 0, limit = (1 << n) - 1; X <= limit; X++)
{
int sum = 0;
for (int Y = 0; Y <= limit; Y++)
sum += F[Y] * G[X ^ Y];
ans = min(sum, ans);
}
```
继续更换枚举方式,枚举 $X\text{ xor }Y$ 的状态:
$$
\begin{aligned}
&\displaystyle\min_{X=0}^{2^n-1}\sum_{Y=0}^{2^n-1}\sum_{Z=0}^{2^n-1}[X\text{ xor }Y=Z]{F_Y}\times{G_Z}\\
&\displaystyle\min_{X=0}^{2^n-1}\sum_{Y=0}^{2^n-1}\sum_{Z=0}^{2^n-1}[X\text{ xor }Y\text{ xor }Y=Z\text{ xor }Y]{F_Y}\times{G_Z}\\
&\displaystyle\min_{X=0}^{2^n-1}\sum_{Y\text{ xor }Z=X}{F_Y}\times{G_Z}
\end{aligned}
$$
$\displaystyle\sum_{Y\text{ xor }Z=X}{F_Y}\times{G_Z}$ 卷积形式,$\operatorname{FWT}$ 即可。
时间复杂度 $O(2^n\log{2^n})=O(2^nn)$。
### Code
```cpp
#include <bits/stdc++.h>
using namespace std;
const int M = 1e5 + 5;
#define ll long long
#define popcount __builtin_popcount
inline bool read()
{
char ch = getchar();
while (!isdigit(ch)) ch = getchar();
return ch - '0';
}
int n, m, l;
int S[M];
ll F[1 << 20], G[1 << 20];
void FWT_XOR(ll *A, const int &opt) /* +1->FWT;-1->IFWT */
{
for (int i = 1; i < l; i <<= 1)
{
for (int j = 0; j < l; j += (i << 1))
{
for (int k = j; k < j + i; k++)
{
ll x = A[k], y = A[k + i];
A[k] = (x + y) / (opt == -1 ? 2 : 1);
A[k + i] = (x - y) / (opt == -1 ? 2 : 1);
}
}
}
}
signed main()
{
cin >> n >> m;
l = 1 << n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
S[j] = S[j] << 1 | read();
for (int i = 1; i <= m; i++) ++F[S[i]];
for (int i = 0; i < l; i++) G[i] = min(popcount(i), n - popcount(i));
FWT_XOR(F, 1), FWT_XOR(G, 1);
for (int i = 0; i < l; i++) F[i] *= G[i];
FWT_XOR(F, -1);
cout << *min_element(F, F + l);
return 0;
}
```
## [CF1119H:Triple](https://www.luogu.com.cn/problem/CF1119H)
### 题目
给定 $3$ 个正整数 $x,y,z$,又给定 $n$ 个数组,第 $i$ 个数组中有 $x$ 个 $a_i$,$y$ 个 $b_i$,$z$ 个 $c_i$。现在求出每个数组内各取出一个数字,这些数的 $\operatorname{xor}$ 和为 $t,t\in[0,2^k)$ 的方案数。
$1\leqslant n\leqslant 10^5,1\leqslant k\leqslant 17$。
输入:
第 $1$ 行:$n,k$。
第 $2$ 行:$x,y,z$。
第 $3$ ~ $n+2$ 行:每行 $3$ 个整数。$a_i,b_i,c_i$。
输出:
共 $1$ 行:一行 $2^k-1$ 个整数,第 $i$ 个数表示 $t=i-1$ 的方案数。
### 思路
考虑到题目中给定了只有 $3$ 个位置有贡献。
第 $i$ 个数组第 $j$ 项的贡献是:
$$
\begin{aligned}
\operatorname{FWT}_{i,j}
&=\displaystyle\sum_{s=0}^{2^k-1}(-1)^{\operatorname{pop}(j\&s)}f_s\\
&=(-1)^{\operatorname{pop}(j\&a_i)}x+(-1)^{\operatorname{pop}(j\&b_i)}y+(-1)^{\operatorname{pop}(j\&c_i)}z
\end{aligned}
$$
根据这个式子,将每个式子**沃尔什正变换**后再点乘,时间复杂度 $O((n+k)2^k)$,时间复杂度不能接受。
考虑总的贡献就是:
$$
\begin{aligned}
S&=\prod_{i=1}^{n}\operatorname{FWT}_i\\
S_j&=\prod_{i=1}^{n}((-1)^{\operatorname{pop}(j\&a_i)}x+(-1)^{\operatorname{pop}(j\&b_i)}y+(-1)^{\operatorname{pop}(j\&c_i)}z)\\
\end{aligned}
$$
所以直接考虑 $(-1)^x$ 的正负性的话上面的多项式对应了 $8$ 种情况:
$$
\begin{aligned}
x+y+z\\
x+y-z\\
x-y+z\\
x-y-z\\
-x+y+z\\
-x+y-z\\
-x-y+z\\
-x-y-z\\
\end{aligned}
$$
貌似不太好处理,这里我们使用了一个小技巧:输入时每次让 $a_i,b_i,c_i$ 都异或上 $a_i$,发现 $a_i\text{ xor }a_i=0,(-1)^0=1$,这样就保证了 $x$ 前的系数永远是 $1$,情况就变为了 $4$ 种。因为开始异或上了 $a_i$ 且 $a_i,b_i,c_i$ 对应的是多项式的下标,所以最后输出答案时让多项式的下标异或上 $\oplus_{i=1}^{n}a_i$ 就行了。
那现在的 $4$ 种情况就是:
$$
\begin{aligned}
x+y+z\\
x+y-z\\
x-y+z\\
x-y-z\\
\end{aligned}
$$
我们分别统计这 $4$ 种情况在第 $i$ 个多项式的出现的个数,下面记作 $c_{[1,4]}$,快速幂就可以求出当前第 $i$ 个多项式的**点值**。
那现在 $S$ 的第 $j$ 项的贡献就是:
$$
S_j=(x+y+z)^{c1}\times(x+y-z)^{c2}\times(x-y+z)^{c3}\times(x-y-z)^{c4}
$$
首先可以确定,$x,y,z$ 的取值与 $c_{[1,4]}$ 无关,所以代入特值解方程:
$$
\begin{aligned}
S_j&=\prod_{i=1}^{n}(x+(-1)^{\operatorname{pop}(j\&(a_i\wedge b_i))}y+(-1)^{\operatorname{pop}(j\&(a_i\wedge c_i))}z)\\
\end{aligned}
$$
$x=1,y=0,z=0$,得到 $S_j=\displaystyle\prod_{i=1}^{n}x$,此时考虑 $x$。
$$
\begin{aligned}
c_1+c_2+c_3+c_4&=n
\end{aligned}
$$
$x=0,y=1,z=0$,此时 $S_j=\displaystyle\prod_{i=1}^{n}(-1)^{\operatorname{pop}(j\&(a_i\wedge b_i))}$,此时考虑的是 $y$。
$$
\begin{aligned}
c_1+c_2-c_3-c_4
&=\displaystyle\sum_{i=1}^{n}\operatorname{FWT}_{i,j}\\
&=\displaystyle\sum_{i=1}^{n}(-1)^{\operatorname{pop}(j\&(a_i\wedge b_i))}\\
&=T_1
\end{aligned}
$$
$x=0,y=0,z=1$,此时 $S_j=\displaystyle\prod_{i=1}^{n}(-1)^{\operatorname{pop}(j\&(a_i\wedge c_i))}$,考虑 $z$。
$$
\begin{aligned}
c_1-c_2+c_3-c_4
&=\displaystyle\sum_{i=1}^{n}\operatorname{FWT}_{i,j}\\
&=\displaystyle\sum_{i=1}^{n}(-1)^{\operatorname{pop}(j\&(a_i\wedge c_i))}\\
&=T_2
\end{aligned}
$$
$3$ 个方程无法解出**四元一次**方程,再构造一种情况:
$x=0,y=1,z=1$,此时 $S_j=\displaystyle\prod_{i=1}^{n}(-1)^{\operatorname{pop}(j\&(a_i\wedge b_i))}(-1)^{\operatorname{pop}(j\&(a_i\wedge c_i))}$,将 $(2)(3)$ 卷积,同时考虑 $y,z$。
$$
\begin{aligned}
c_1-c_2-c_3+c_4
&=\displaystyle\sum_{i=1}^{n}\operatorname{FWT}_{i,j}\\
&=\displaystyle\sum_{i=1}^{n}(-1)^{\operatorname{pop}(j\&(a_i\wedge b_i))}(-1)^{\operatorname{pop}(j\&(a_i\wedge c_i))}\\
&=\displaystyle\sum_{i=1}^{n}(-1)^{\operatorname{pop}(j\&(a_i\wedge b_i\wedge a_i\wedge c_i))}\\
&=\displaystyle\sum_{i=1}^{n}(-1)^{\operatorname{pop}(j\&( b_i\wedge c_i))}\\
&=T_3
\end{aligned}
$$
后 $3$ 种情况的 $T_1,T_2,T_3$ 开始时开 $3$ 个桶记录然后**快速沃尔什正变换**就行了。
然后解方程:
$$
\begin{cases}
c_1+c_2+c_3+c_4=n\\
c_1+c_2-c_3-c_4=T_1\\
c_1-c_2+c_3-c_4=T_2\\
c_1-c_2-c_3+c_4=T_3\\
\end{cases}
$$
最后解得:
$$
\begin{cases}
c_1=\frac{n+T_1+T_2+T_3}{4}\\
c_2=\frac{n+T_1-T_2-T_3}{4}\\
c_3=\frac{n-T_1+T_2-T_3}{4}\\
c_4=\frac{n-T_1-T_2+T_3}{4}\\
\end{cases}
$$
于是就求出了 $S_i$,最后 $\operatorname{IFWT}$ 回去,下标异或上 $\oplus_{i=1}^{n}a_i$ 就行了。
### Code
```cpp
#include <bits/stdc++.h>
using namespace std;
namespace IO {}
using namespace IO;
const int N = (1 << 17) + 10;
const int MOD = 998244353;
const int INV2 = 499122177;
const int INV4 = 748683265;
int T1[N], T2[N], T3[N];
int F[N];
int length;
#define ll long long
ll ksm(int x, int y, ll ans = 1)
{
if (x < 0) x += MOD;
if (y < 0) y += MOD;
while (y > 0)
{
if (y & 1)
ans = ans * x % MOD;
x = 1ll * x * x % MOD;
y >>= 1;
}
return ans;
}
void FWTXOR(int *A, int opt)
{
for (int i = 1; i < length; i <<= 1)
{
for (int j = 0; j < length; j += (i << 1))
{
for (int k = j; k < j + i; k++)
{
ll x = 1ll * A[k] * ((opt == -1) ? INV2 : 1) % MOD;
ll y = 1ll * A[k + i] * ((opt == -1) ? INV2 : 1) % MOD;
A[k] = (x + y + MOD) % MOD;
A[k + i] = (x - y + MOD) % MOD;
}
}
}
}
signed main()
{
ll n, k, x, y, z, XOR = 0;
read(n, k, x, y, z);
length = 1 << k;
for (int i = 1, a, b, c; i <= n; i++)
{
read(a, b, c);
XOR ^= a;
T1[b ^ a]++;
T2[c ^ a]++;
T3[b ^ c]++;
}
FWTXOR(T1, 1);
FWTXOR(T2, 1);
FWTXOR(T3, 1);
int s1 = (x + y + z) % MOD;
int s2 = (x + y - z) % MOD;
int s3 = (x - y + z) % MOD;
int s4 = (x - y - z) % MOD;
for (int i = 0; i < length; i++)
{
int c1 = 1ll * (n + T1[i] + T2[i] + T3[i]) % MOD * INV4 % MOD;
int c2 = 1ll * (n + T1[i] - T2[i] - T3[i]) % MOD * INV4 % MOD;
int c3 = 1ll * (n - T1[i] + T2[i] - T3[i]) % MOD * INV4 % MOD;
int c4 = 1ll * (n - T1[i] - T2[i] + T3[i]) % MOD * INV4 % MOD;
F[i] = ksm(s1, c1) % MOD * ksm(s2, c2) % MOD * ksm(s3, c3) % MOD * ksm(s4, c4) % MOD;
}
FWTXOR(F, -1);
for (int i = 0; i < length; i++)
print(F[XOR ^ i], ' ');
return 0;
}
```
# Others
【题目】:
例题:
[CF1119H](https://www.luogu.com.cn/problem/CF1119H)
[CF662C](https://www.luogu.com.cn/problem/CF662C)
[CF453D](https://www.luogu.com.cn/problem/CF453D)
模板:
[P4717](https://www.luogu.com.cn/problem/P4717)
【参考 Blog】:[快速沃尔什变换(FWT)详详详解-Hypoc](https://blog.csdn.net/a_forever_dream/article/details/105110089)
【初稿】:2022.9.18
【修改】:2022.12.31~2023.1.1