浅谈 Splay (2)
wangyibo201026
·
·
个人记录
开头的开头
为啥要学习 \text{Splay} 这种代码不好理解的平衡树,首先我们论一下 \text{FHQ} 的优点:
- 好理解。
- 好实现。
- 拓展广。
但是同样也有一些缺点,那就是随机取权值的情况下会导致常数及其的大,搞不好搞出一条链来就直接挂掉了,可以说非常的看人品,所以我们有了新的平衡树:旋转平衡树。
1. 码量适中。
2. 树旋转的复杂度**较**快,虽然有很大的常数。
3. 适用范围同样很广,包括但不限于解决区间问题,用来维护 $\text{LCT}$ 等。
但是同样也有很明显的缺点:
1. 简单版不好理解。
2. 不能可持久化(虽然好像现在平衡树可持久化的复杂度都是错的)。
好了,如果你是一个对 $\text{Splay}$ 有着极度热爱的人,那就继续往下看。
为啥说这个东西是噩梦呢?因为 $\text{Splay}$ 每时每刻都要用到它,所以千万要记牢。
首先我们要知道树旋转的本质是什么,是在不改变二叉搜索树的性质情况下将结构改变,然后旋转分为两种,左旋和右旋,二者是可以互通的。
树旋转的本质目的是插入一个结点到平衡树里后,能够移动到某个指定位置。
## 永恒的噩梦——树旋转
### 左旋
左旋在 $\text{Splay}$ 里也被称为 $zag$,具体方式如图:
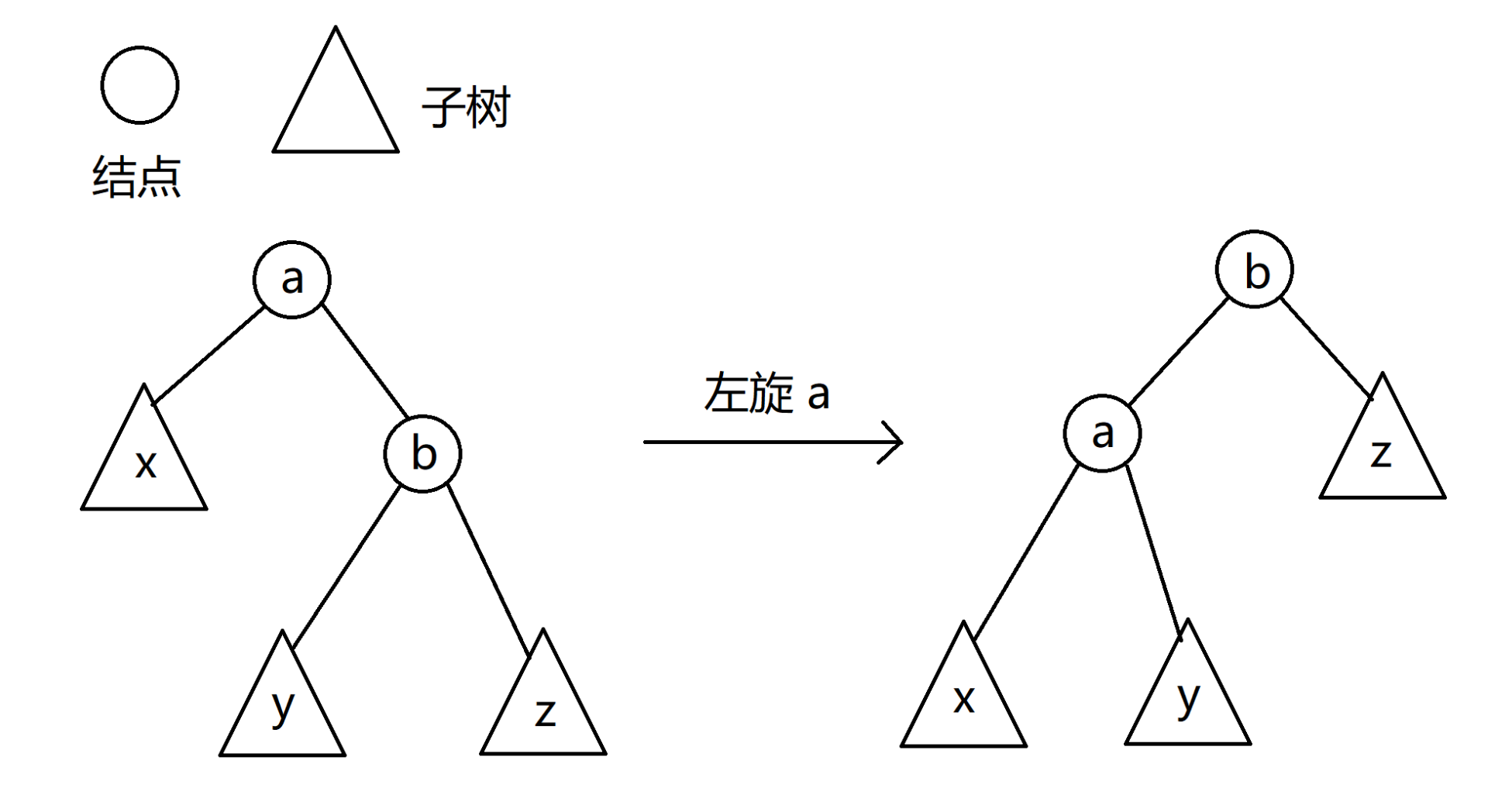
有一个很好记的方法,出自 AgOH 大佬视频,叫左旋左旋拎右左挂右,其实不难,就是将 $b$ 拎起来,然后将 $b$ 的左子树 $y$ 挂到 $a$ 的右子树上,这样就完成了左旋。
不难发现这样子仍保持二叉搜索树的大小性质。
代码:
```cpp
void zag(int &node){
int r = spl[node].r; //好好理解一下
spl[node].r = spl[r].l;
spl[r].l = node;
node = r;
update(spl[node].l); //这里是更新节点子树内大小
update(node);
}
```
### 右旋
右旋在 $\text{Splay}$ 里也被称为 $zig$,具体方式如图:
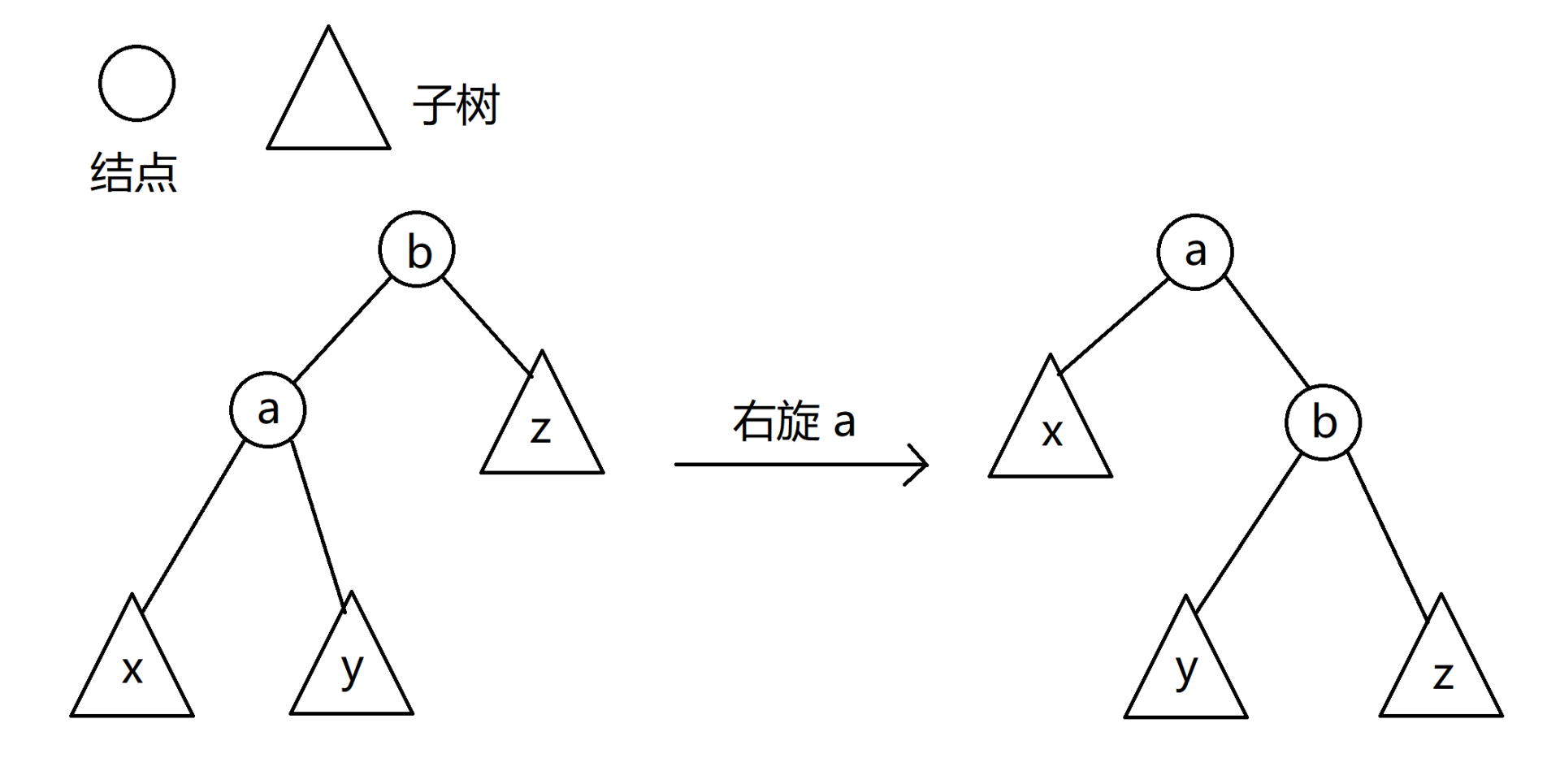
不难发现其实就是反过来,同样选自 AgOH 的背记口语:右旋拎左右挂左,其意义仍然一样,这里就不过多重复。
代码:
```cpp
void zig(int &node){
int l = spl[node].l;
spl[node].l = spl[l].r;
spl[l].r = node;
node = l;
update(spl[node].r);
update(node);
}
```
## 单旋的进阶——双旋
据说 $\text{Splay}$ 的发明者发现单旋的复杂度是不对的,从而发明了双旋,原因以下再讲。
其中双旋有两种,分别为异构调整和同构调整。
### 异构调整
上面说过,旋转的目的是要将插入结点移动到指定结点,那么在这条链上可能会出现几种情况,其中不在同一条直线上的有两种:
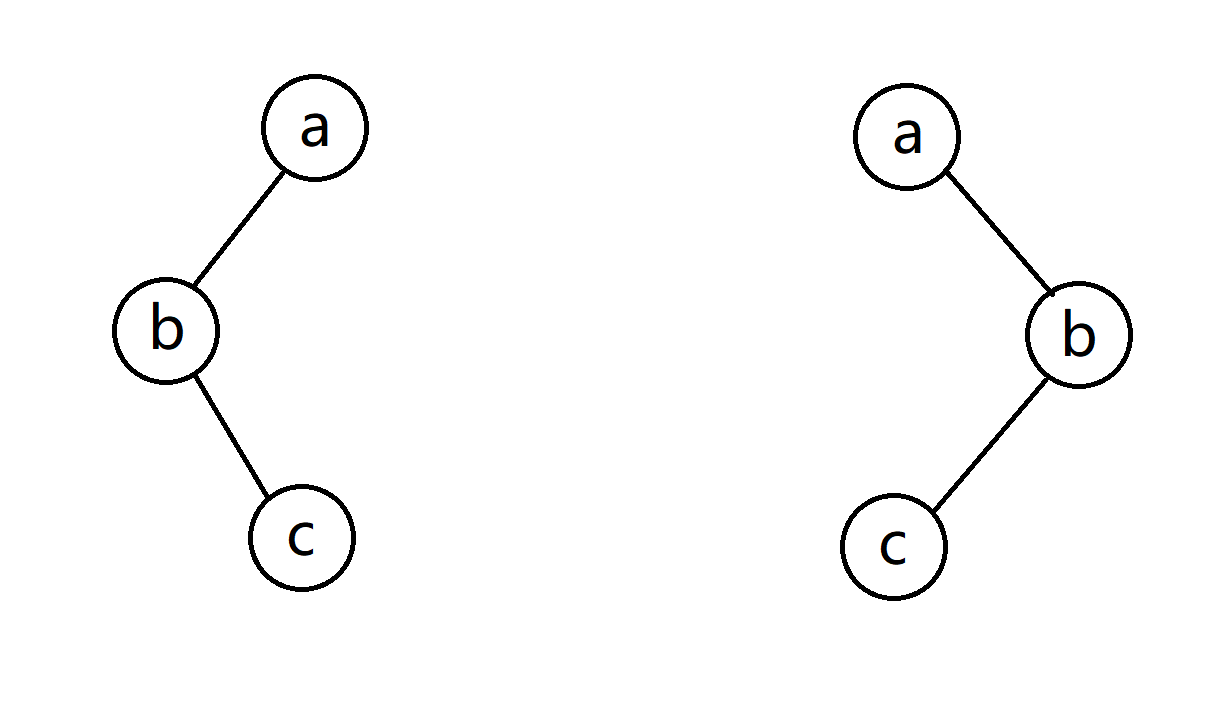
第一种是往左边扭,第二种是往右边扭。
处理方法和普通旋转一样,针对第一种,先对 $b$ 左旋,再对 $a$ 右旋,第二种,先对 $b$ 右旋,再对 $a$ 左旋。
容易发现,这种情况和普通的旋转上去之后的结构并无区别。
### 同构调整
上面讲了异构调整,是之字形的,那同构调整就是一条直线,具体情况如图所示:
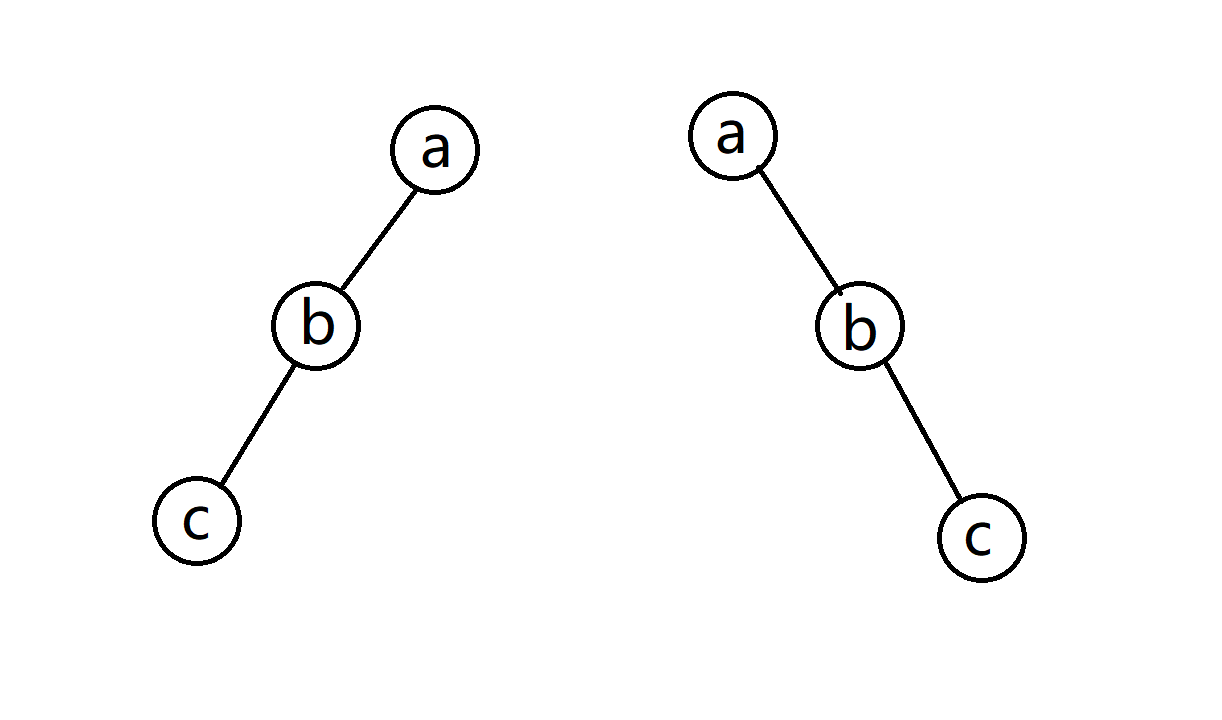
针对于第一种情况,先将 $a$ 右旋,再将 $b$ 右旋就行了,第二种情况,先将 $a$ 左旋,再将 $b$ 左旋即可。
---
上面旋转完之后可以自己画画图。
以上的旋转目的都是将结点 $c$ 旋转至最上层,那我们看看这单旋和双旋两者的区别,容易发现对于异构调整,旋转完之后层数没变,我们清楚的知道平衡树的复杂度大多是依靠树高的,所以这跟普通旋转几乎没区别,但同构调整转完后却是这样的:
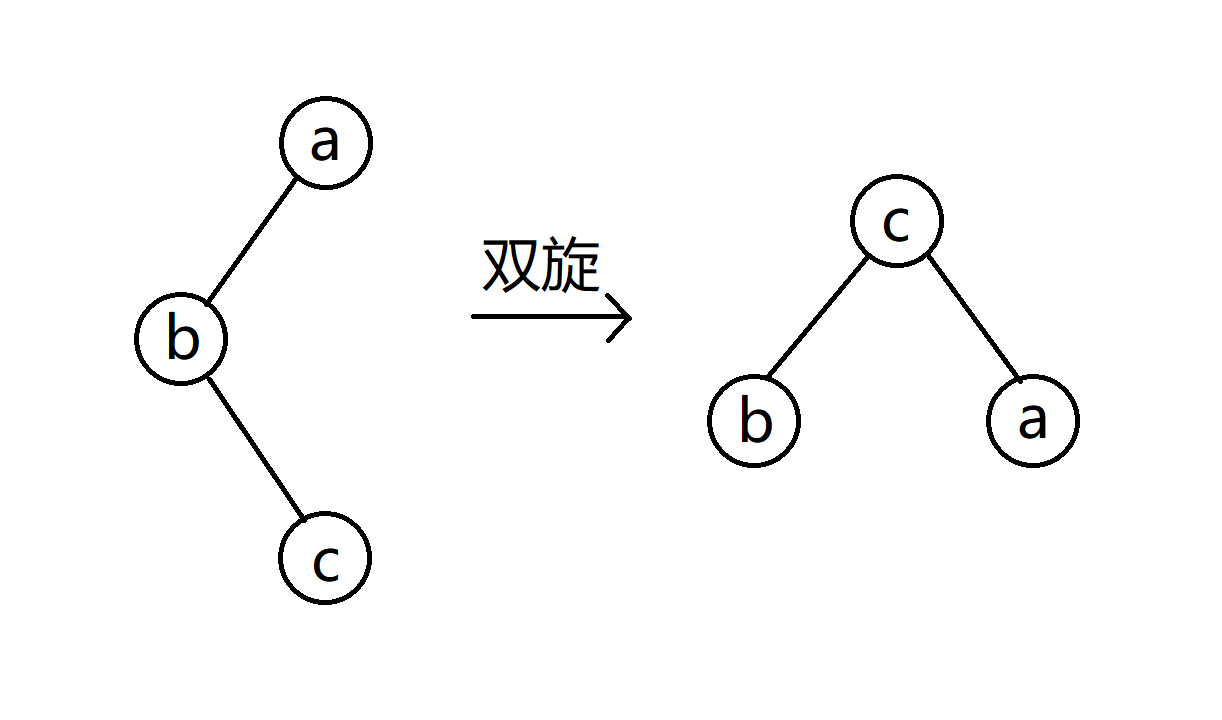
我们发现如果把 $c$ 结点一直这样旋转到根节点,那么树高大致减少一半,所以 $\text{Splay}$ 的均摊复杂度是 $O(n\log_2n)$ 的。
## $\text{Splay}$ 的操作。
有几种必要的操作,看吧。一些基础化的操作就不讲了,比如子树更新大小之类的,在下面都会有解释。
### 旋转大综合
我们发现如果要写单旋双旋真的是忒复杂了啊,一共四种情况,谁的不愿意写,所以我们写一个旋转大总和,先把代码放上来:
```cpp
void rotate(int x){
int fa = spl[x].fa, ffa = spl[fa].fa, k = ident(x, fa);
connect(spl[x].ch[k ^ 1], fa, k);
connect(x, ffa, ident(fa, ffa));
connect(fa, x, k ^ 1);
update(fa);
update(x);
}
```
其中 $ident$ 为判断父子关系的函数,左儿子为 $0$,右儿子为 $1$。$connect$ 为建立父子关系的函数,$k$ 的参数跟上面一样。
这个真没什么好讲的,可以自己针对上面的双旋模拟一下,就会发现是对的。