【x义x讲坛】多项式学习笔记(上)
x义x
·
2019-09-20 15:26:02
·
个人记录
\color{green}\Large\texttt{『菜鸡的blog』}
参考资料包括但不限于:
0x01.法法特 FFT可以快速地把一个系数表示的多项式转化为点值表示(其实就是代n 个值进去)
假设n 是偶数。
我们现在希望把\omega_n^0,\omega_n^1,\dots,\omega_n^{n-1} (n 次单位根)这几个值代入A(x) 。
显然
A(x)=(a_0+a_2x^2+a_4x^4+\dots)+x(a_1+a_3x^2+a_5x^4+\dots)
称:
\begin{cases}A_0(x)=a_0+a_2x+a_4x^2+\dots\\A_1(x)=a_1+a_3x+a_5x^2+\dots\end{cases}
那么显然
A(x)=A_0(x^2)+xA_1(x^2)
现在再把\omega ^k_n 带进去。
A(\omega ^k_n)=A_0(\omega^{2k}_n)+\omega ^k_nA_1(\omega ^{2k}_n)
运用结论:\omega_n^k=\omega_{2n}^{2k} 。
A(\omega ^k_n)=A_0(\omega^k_\frac n 2)+\omega ^k_nA_1(\omega ^k_\frac n 2)
同理,我们把\omega_n^{k+\frac n 2} 带进去可以得到:
A(\omega ^{k+\frac n 2}_n)=A_0(\omega^{2k+n}_n)+\omega ^{k+\frac n 2}_nA_1(\omega^{2k+n}_n)
显然地,\omega ^n_n=1 ,又因为\omega_n^{k+\frac n 2}=-\omega_n^k ,那么容易得出
A(\omega ^{k+\frac n 2}_n)=A_0(\omega^k_\frac n 2)-\omega ^k_nA_1(\omega^k_\frac n 2)
再次进行比较:
\begin{cases}A(\omega ^k_n)=A_0(\omega^k_\frac n 2)+\omega ^k_nA_1(\omega ^k_\frac n 2)\\A(\omega ^{k+\frac n 2}_n)=A_0(\omega^k_\frac n 2)-\omega ^k_nA_1(\omega^k_\frac n 2)\end{cases}
所以当我们算第一个柿子的时候,我们可以同时算出第二个柿子!
所以,我们把“把n 个值代入一个n 次多项式A(x) ”的问题转化为了两个“将\frac n 2 个值代入一个\frac n 2 次多项式A_{0/1}(x) ”的问题,需要O(n) 的复杂度来合并。根据主定理可以得到最终复杂度为O(n\log n) 。
0x02.逆法法特 现在我们需要把
\begin{cases}(~\omega_n^0,y_0~)\\(~\omega_n^1,y_1~)\\\dots\\(~\omega_n^{n-1},y_{n-1}~)\end{cases}
转回系数表示法。
设
c_k=\sum_{i=0}^{n-1}y_i(\omega_n^{-k})^i
其实也就是说我们构造了一个多项式
B(x)=y_0+y_1x+y_2x^2+\dots
,而它的点值表示就是
\begin{cases}(~\omega_n^0,c_0~)\\(~\omega_n^{-1},c_1~)\\\dots\\(~\omega_n^{1-n},c_{n-1}~)\end{cases}
。写得再明白点就是:
\begin{cases}(~\omega_n^0,c_0~)\\(~\omega_n^{n-1},c_1~)\\\dots\\(~\omega_n^{1},c_{n-1}~)\end{cases}
显然可以FFT得到。
然后开始推柿子。
c_k=\sum_{i=0}^{n-1}y_i(\omega_n^{-k})^i
$$c_k=\sum_{i=0}^{n-1}\left((\omega_n^{-k})^i*\sum_{j=0}^{n-1}a_j(\omega_n^i)^j\right)$$
$(\omega_n^{-k})^i=\omega_n^{-ki}$和$(\omega_n^i)^j=\omega_n^{ij}$显然可以消一下:
$$c_k=\sum_{i=0}^{n-1}\left(\sum_{j=0}^{n-1}a_j(\omega_n^{j-k})^i\right)$$
换求和号顺序:
$$c_k=\sum_{j=0}^{n-1}\left(a_j\sum_{i=0}^{n-1}(\omega_n^{j-k})^i\right)$$
里边那个求和号是$\sum_{i=0}^{n-1}x^i$,根据等比数列求和公式(它是可以推广到复数域的):
$$\sum_{i=0}^{n-1}x^i=\dfrac {1-x^n}{1-x}\quad(x\neq1)$$
把$\omega_n^{j-k}\quad(j\neq k)$带进去得
$$\text{里面那个求和号}=\dfrac {1-\omega^{nk}_n}{1-\omega^k_n}$$
$\omega_n^n=1$,所以里面那个求和号就是零。
所以只有当$j=k$时才有贡献,即:
$$c_k=na_k$$
完成!
### **0x03.法法特的优化**
按照上面的方法,我们可以得到一个复杂度正确但是运行效率,所用空间都不是很优秀的递归版实现。
观察一下运算顺序:
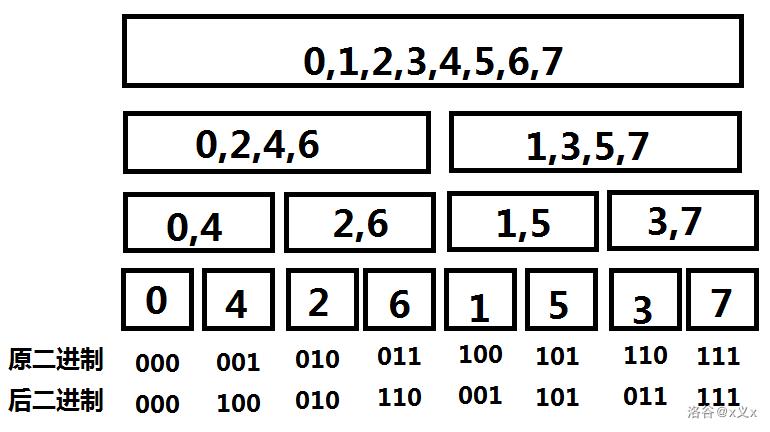
发现后来的下标就是原来的下标二进制翻转一下!
二进制翻转随便乱搞即可,于是就可以得到一个较为优秀的迭代实现版。
另外,有趣的是,FFT和逆FFT在代码上非常相近以至于只需要改一个地方……
```cpp
#include <bits/stdc++.h>
#define db double
using namespace std;
const int maxN=10000010;
const db Pi=acos(-1.0);
struct Cpl{
db r,i;
Cpl (db r0=0,db i0=0){r=r0;i=i0;}
Cpl operator +(const Cpl b)const{return Cpl(r+b.r,i+b.i);}
Cpl operator -(const Cpl b)const{return Cpl(r-b.r,i-b.i);}
Cpl operator *(const Cpl b)const{return Cpl(r*b.r-i*b.i,r*b.i+i*b.r);}
} a[maxN],b[maxN];
int N,M;
int X=1,len;
int R[maxN];
void FFT(Cpl A[],int flg){
for(int i=0;i<X;i++)
if(i<R[i]){Cpl t=A[i];A[i]=A[R[i]];A[R[i]]=t;}
for(int mid=1;mid<X;mid<<=1){
Cpl W(cos(Pi/mid),flg*sin(Pi/mid));
for(int j=0;j<X;j+=(mid<<1)){
Cpl sum(1,0);
for(int k=0;k<mid;k++){
Cpl A0=A[j+k],A1=sum*A[j+mid+k];
A[j+k]=A0+A1;A[j+mid+k]=A0-A1;
sum=sum*W;
}
}
}
}
int main(){
scanf("%d%d",&N,&M);
while(X<=N+M) X<<=1,len++;
for(int i=0;i<X;i++) R[i]=(R[i>>1]>>1)|((i&1)<<(len-1));
for(int i=0;i<=N;i++) scanf("%lf",&a[i].r);
for(int i=0;i<=M;i++) scanf("%lf",&b[i].r);
FFT(a,1);FFT(b,1);
for(int i=0;i<=X;i++) a[i]=a[i]*b[i];
FFT(a,-1);
for(int i=0;i<=N+M;i++)
printf("%d ",(int)(a[i].r/X+0.5));
return 0;
}
```
另外,如果多项式系数都是整数且题目规定答案$\mod p$,那么可以使用$p$的**原根**代替单位根来进行运算来避免精度等问题。设$g$为$p$的原根,那么直接用$g^\frac {p-1} n\pmod p$代替$\omega_n^1$即可。($\frac {p-1}n$需向下取整)这样的话这个算法就改叫呢特特了。
### **0x04.法法特的一些应用**
通式:搞出奇怪的函数->寻找卷积形式(必要时翻转序列)->FFT搞出
### **0x05.多项式求逆**
首先,由于在很多问题(比如生成函数题)中我们只关心某多项式的前$n$项,因此,引入符号$\mod x^n$来表示一个多项式的前$n$项是自然的。(逐渐数学参考书化)
$\mod x^n$意义下的多项式加法、乘法都可以直接通过正常的多项式加法、乘法拓展得到,然而,我们发现除法非常难搞。然而接下来我们会发现除法是十分必要的。
要有除法必须要先有乘法逆元。我们定义,满足:
$$A*B=1\pmod {x^n}$$
的$A,B$互为乘法逆元。现在考虑如何快速求乘法逆元。
假设
$$A*B=1\pmod {x^n}$$
$$A*B'=1\pmod {x^{\lceil \frac n 2\rceil}}$$
现在我们试图用$A,B'$表示$B$。
显然有
$$A*(B-B')=0\pmod {x^{\lceil \frac n 2\rceil}}$$
显然$A$的常数项就不可能是0,否则不可能有$A*B=1\pmod {x^n}$,所以$(B-B')$的常数项为0;
$A*(B-B')$的一次项是$A$的常数项$\times(B-B')$的一次项$+A$的一次项$\times(B-B')$的常数项。显然$A$的一次项$\times(B-B')$的常数项为0,我们又已经论证过$A$的常数项不为0,所以要使$A*(B-B')$的一次项为0必然有$(B-B')$的一次项为0;
……
依次类推,我们得出结论:
$$B-B'=0\pmod {x^{\lceil \frac n 2\rceil}}$$
平方一下,容易知道(注意我们$\mod {}$了什么)
$$(B-B')^2=B^2-2BB'+B'^2=0\pmod{x^n}$$
两边乘$A$来降低$B$的次数:
$$B=2B'-AB'^2\pmod{x^n}$$
Oh♂That's♂Good,但是请千万记住那个$\pmod{x^n}$,请千万在算出$B$后把$x^n$以及更高的项强行赋成0,我tm因为这个原因调了一下午。
于是分治地计算即可。边界:$A=c$时逆元为$\dfrac 1 c$。
千万认真看这个柿子的推导过程,记住每一个多项式的长度,否则你会在调边界的时候原地爆炸。
代码如下。还是挺漂亮的。想看与其配合的函数请至最下的完整板子。
```cpp
void Inv(int d[],int ans[],int n0){
if(n0==1){ans[0]=qpow(d[0],p-2,p);return;}
Inv(d,ans,n0>>1);
for(int i=0;i<n0;i++) tmpans[i]=ans[i],tmpd[i]=d[i];
NTT(tmpans,0,n0<<1);NTT(tmpd,0,n0<<1);
for(int i=0;i<(n0<<1);i++) tmpans[i]=1LL*tmpans[i]*tmpans[i]%p*tmpd[i]%p;
NTT(tmpans,1,n0<<1);
for(int i=0;i<n0;i++) ans[i]=((ll)ans[i]+ans[i]-tmpans[i]+p)%p;
for(int i=0;i<(n0<<1);i++) tmpans[i]=tmpd[i]=0;
}
```
### **0x06.多项式除法**
于是可以快乐地进行多项式除法啦!
还是先定义一下什么是多项式除法吧。
对于$n$次多项式$A(x)$和$m$次多项式$B(x)$,我们要找到一个$n-m$次多项式$Q(x)$和一个小于$m$次的多项式$R(x)$,满足:
$$A=BQ+R$$
好的我们来切入正题。我们发现$R$非常麻烦,要是没有它我们直接把$B$求个逆元移到等式另一边即可。所以开始变换。
先定义一个记号:$\text{rev}(A)$表示将$A$的高低次项翻转,换句话说,$\text{rev}(A)(x)=x^nA(\dfrac 1 x)$。
首先,肯定有
$$A(\dfrac 1 x)=B(\dfrac 1 x)Q(\dfrac 1 x)+R(\dfrac 1 x)$$
两边乘以$x^n$。
$$x^nA(\dfrac 1 x)=\left[x^mB(\dfrac 1 x)\right]\cdot\left[x^{n-m}Q(\dfrac 1 x)\right]+x^{n-m+1}\cdot x^{m-1}R(\dfrac 1 x)$$
全换成$\text{rev}$。
$$\text{rev}(A)(x)=\text{rev}(B)(x)\text{rev}(Q)(x)+x^{n-m+1}\text{rev}(R)(x)$$
把这个柿子丢到$\mod {x^{n-m+1}}$次下就可以甩掉$R$了!而且因为$Q$只有$n-m$次我们不需要担心$Q$的正确性。
$$\text{rev}(A)(x)=\text{rev}(B)(x)\text{rev}(Q)(x)\pmod {x^{n-m+1}}$$
两边乘以$\text{rev}(B)^{-1}$,完成。
$R$就直接$A-BQ$即可。
代码过于简单就不放了。完整板子里也没有。(那你还管这叫完整板子???)
### **0x07.多项式 ln**
我们发现,原来我们$\ln$的定义是$e^x=a\rightarrow x=\ln a$,但是我们(目前)根本不知道$e^{A(x)}$是什么鬼玩意,更不可能定向找到满足这个柿子的$A(x)$,按照这种方法求解完全不现实。
我们发现:$(\ln f(x))'=\dfrac {f'(x)}{f(x)}$,我们会多项式求导也会多项式求逆元也会多项式积分,这很优良,所以:
若$B(x)=\ln A(x)$,则可以通过
$$B(x)=\int\dfrac {A'(x)}{A(x)} \text{d}x$$
计算出$B(x)$。
你会发现我们这样并不能求出$B(x)$的常数项,不过这无伤大雅,把$x=0$带进$A(x)$会发现$\ln a_0=b_0$,但模意义下的$\ln$比较难搞,所以一般来讲题目会保证$a_0=1$,使得$b_0=0$。
```cpp
void Ln(int d[],int ans[],int n0){
Der(d,derd,n0);Inv(d,invd,n0);
NTT(derd,0,n0<<1);NTT(invd,0,n0<<1);
for(int i=0;i<(n0<<1);i++) derd[i]=1LL*derd[i]*invd[i]%p;
NTT(derd,1,n0<<1);Int(derd,ans,n0);
for(int i=0;i<(n0<<1);i++) derd[i]=invd[i]=0;
}
```
### **0x08.多项式上的牛顿迭代法**
已知一个函数$f(x)$,求一个多项式$A(x)$满足:
$$f(A(x))=0\pmod{x^n}$$
假设我们已经求出$A'(x)$使得$f(A'(x))=0\pmod {x^{\lceil\frac n 2\rceil}}$。
问题是$f(x)$不一定是多项式,(一般来讲)用我们目前的工具无法处理。然而我们实际上是可以把一个函数变为多项式的,这个操作叫做泰勒展开。记$f^{(i)}(x)$是$f(x)$的$i$阶导。
$$f(x)=\sum_{i=0}^n\dfrac{f^{(i)}(x_0)(x-x_0)^i}{i!}+R_n(x)$$
是$f(x)$在$x=x_0$处的$n$阶泰勒展开,后面那个东西$R_n(x)$叫做余项,是$(x-x_0)^n$的高阶无穷小,~~意思就是一般来讲我们可以当它不存在。~~
好的,那么把最开始那个柿子在$A'(x)$处展开一下得到:
$$f(A(x))=\sum_{i=0}^n\dfrac{f^{(i)}(A'(x))(A(x)-A'(x))^i}{i!}$$
显然有$A(x)-A'(x)=0\pmod{x^{\lceil\frac n 2\rceil}}$,于是$(A(x)-A'(x))^2=0\pmod{x^n}$。所以上面那个柿子的一大堆项在$\pmod{x^n}$下全是0,得到:
$$f(A(x))=0=f(A'(x))+f^{(1)}(A'(x))(A(x)-A'(x))\pmod{x^n}$$
$$A(x)=A'(x)-\dfrac{f(A'(x))}{f^{(1)}(A'(x))}\pmod{x^n}$$
这和牛顿迭代法$x=x_0-\dfrac {f(x_0)}{f'(x_0)}$很像,于是称作多项式上的牛顿迭代法。
边界:$n=1$时,$A(x)$就是$f(x)$的一个零点。
这允许我们把一些函数的反函数推广到多项式上。
### **0x09.多项式 exp**
设$B(x)=e^{A(x)}$。那么有
$$\ln B(x)-A(x)=0$$
注意$A(x)$视为一个常数。
于是设计函数$f(B(x))=\ln B(x)-A(x)$,按上面的牛迭法得到:
$$B(x)=B'(x)(1-\ln B'(x)+A(x))$$
```cpp
void Exp(int d[],int ans[],int n0){
if(n0==1){ans[0]=1;return;}
Exp(d,ans,n0>>1);
Ln(ans,lnans,n0);
for(int i=0;i<n0;i++) lnans[i]=(d[i]-lnans[i]+p)%p;
lnans[0]=(lnans[0]+1)%p;
NTT(lnans,0,n0<<1);NTT(ans,0,n0<<1);
for(int i=0;i<(n0<<1);i++) ans[i]=1LL*ans[i]*lnans[i]%p;
NTT(ans,1,n0<<1);
for(int i=n0;i<(n0<<1);i++) ans[i]=lnans[i]=0;
}
```
### **0x0a.多项式开根号**
设$B(x)=\sqrt {A(x)}$。那么有
$$B^2(x)-A(x)=0$$
于是设计函数$f(B(x))=B^2(x)-A(x)$,得到:
$$B(x)=\dfrac {B'(x)} 2+\dfrac{A(x)}{2B'(x)}$$
边界需要用到二次剩余,于是你又得写一个BSGS,十分难受。我们还可以用下面的方法。
### **0x0b.多项式快速幂**
利用
$$a^k=e^{k\ln a}$$
我们可以快速计算多项式的幂:
$$A^k(x)=e^{k\ln A(x)}$$
分类讨论一下:
- $a_0=1$。这已经很优良了,直接$\ln$。
- $a_0\ge2$。$A^k(x)=a_0^k\cdot (\dfrac {A(x)}{a_0})^k$,转化为情况1。
- $a_0=0$。$A^k(x)=x^k\cdot(\dfrac{A(x)}{x})^k$,并继续讨论$\dfrac{A(x)}{x}$。
$k=\dfrac 1 2$的情况即为多项式开根号。这很优良。
### **0x0c.多项式三角函数/双曲函数/反三角函数**
3道凑数题。
根据欧拉公式$e^{i\theta}=\cos\theta+i\sin\theta$,有:
$$\begin{cases}\cos x=\dfrac {e^{ix}+e^{-ix}} 2\\\sin x=\dfrac {e^{ix}-e^{-ix}} 2\end{cases}$$
$i$是什么?不过是一个满足$i^2=-1$的数而已。你当然可以跑一下二次剩余,但事实上它是$g^{\frac{p-1}4}$。
双曲函数则更为sb,把$ix$换成$x$即可。
反三角函数也挺好推的。
### **0x0d.法哇特**
这是多项式乘法:
$$C[i]=\sum_{j+k=i}A[j]B[k]$$
但是,如果遇到($\lor$是位或,$\land$是位与,$\oplus$是位异或)
$$C[i]=\sum_{j\lor k=i}A[j]B[k]$$
$$C[i]=\sum_{j\land k=i}A[j]B[k]$$
$$C[i]=\sum_{j\oplus k=i}A[j]B[k]$$
则需要FWT出场了。
我们记$(a,b)$是把多项式$a,b$首尾拼接,$A_0,A_1$分别是$A$的前半部分和后半部分。则FFT可表示为
$$F(A)[k]=\begin{cases}A[k]&(n=1)\\\Big(~F(A_0)[k]+w_n^kF(A_1)[k]~,~F(A_0)[k]-w_n^kF(A_1)[k]~\Big)&(otherwise)\end{cases}$$
这个我们已经很熟悉了。
##### **或卷积**
对于或运算下的多项式卷积则应该是(我们用$I$表示其逆变换)
$$F(A)[k]=\begin{cases}A[k]&(n=1)\\\Big(~F(A_0)[k]~,~F(A_0+A_1)[k]~\Big)&(otherwise)\end{cases}$$
$$I(A)[k]=\begin{cases}A[k]&(n=1)\\\Big(~I(A_0)[k]~,~I(A_1-A_0)[k]~\Big)&(otherwise)\end{cases}$$
$A_0+A_1$是多项式加法。
下面是结论。读者有兴趣可以自行证明。
- $F(A+B)=F(A)+F(B)$。
- $F(A\lor B)[k]=F(A)[k]\times F(B)[k]
和FFT有类似的性质。
与卷积 对于与运算下的多项式卷积则应该是
F(A)[k]=\begin{cases}A[k]&(n=1)\\\Big(~F(A_0+A_1)[k]~,~F(A_0)[k]~\Big)&(otherwise)\end{cases}
I(A)[k]=\begin{cases}A[k]&(n=1)\\\Big(~I(A_0-A_1)[k]~,~I(A_0)[k]~\Big)&(otherwise)\end{cases}
下面是结论。
F(A\land B)[k]=F(A)[k]\times F(B)[k]
异或卷积 F(A)[k]=\begin{cases}A[k]&(n=1)\\\Big(~F(A_0+A_1)[k]~,~F(A_0-A_1)[k]~\Big)&(otherwise)\end{cases}
I(A)[k]=\begin{cases}A[k]&(n=1)\\\Big(~\dfrac{I(A_0+A_1)[k]}2~,~\dfrac{I(A_0-A_1)[k]} 2~\Big)&(otherwise)\end{cases}
F(A\oplus B)[k]=F(A)[k]\times F(B)[k]
真的非常漂亮也很好背。代码不放了。
0x0e.板子 P5264AC代码如下。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int p=998244353,maxN=524288;
const int g=3,ig=332748118;
int I,invI;
int W[25][maxN+5],iW[25][maxN+5],inv[maxN+5],R[maxN+5];
int X,x,len;
int N,opt,A[maxN+5],ANSsin[maxN+5],ANScos[maxN+5];
char c;
int qpow(int a,int k,int tt){
int ans=1;
while(k){
if(k&1) ans=1LL*ans*a%tt;
a=1LL*a*a%tt;
k>>=1;
}
return ans;
}
void NTT(int d[],bool flg,int n0){
x=1;len=0;while(x<n0) x<<=1,len++;
for(int i=0;i<x;i++){
R[i]=(R[i>>1]>>1)|((i&1)<<(len-1));
if(i<R[i]) swap(d[i],d[R[i]]);
}
for(int i=1,l=1;i<x;i<<=1,l++)
for(int j=0;j<x;j+=(i<<1))
for(int k=0;k<i;k++){
int a0=d[j+k],a1=1LL*(flg?iW[l][k]:W[l][k])*d[j+i+k]%p;
d[j+k]=(a0+a1)%p;d[j+i+k]=(a0-a1+p)%p;
}
if(flg)
for(int i=0;i<x;i++)
d[i]=1LL*d[i]*inv[x]%p;
}
int tmpans[maxN+5],tmpd[maxN+5];
void Inv(int d[],int ans[],int n0){
if(n0==1){ans[0]=qpow(d[0],p-2,p);return;}
Inv(d,ans,n0>>1);
for(int i=0;i<n0;i++) tmpans[i]=ans[i],tmpd[i]=d[i];
NTT(tmpans,0,n0<<1);NTT(tmpd,0,n0<<1);
for(int i=0;i<(n0<<1);i++) tmpans[i]=1LL*tmpans[i]*tmpans[i]%p*tmpd[i]%p;
NTT(tmpans,1,n0<<1);
for(int i=0;i<n0;i++) ans[i]=((ll)ans[i]+ans[i]-tmpans[i]+p)%p;
for(int i=0;i<(n0<<1);i++) tmpans[i]=tmpd[i]=0;
}
void Der(int d[],int ans[],int n0){
for(int i=0;i<n0;i++) ans[i]=1LL*d[i+1]*(i+1)%p;
}
void Int(int d[],int ans[],int n0){
for(int i=n0-1;i>=0;i--) ans[i+1]=1LL*d[i]*inv[i+1]%p;ans[0]=0;
}
int derd[maxN+5],invd[maxN+5];
void Ln(int d[],int ans[],int n0){
Der(d,derd,n0);Inv(d,invd,n0);
NTT(derd,0,n0<<1);NTT(invd,0,n0<<1);
for(int i=0;i<(n0<<1);i++) derd[i]=1LL*derd[i]*invd[i]%p;
NTT(derd,1,n0<<1);Int(derd,ans,n0);
for(int i=0;i<(n0<<1);i++) derd[i]=invd[i]=0;
}
int lnans[maxN+5];
void Exp(int d[],int ans[],int n0){
if(n0==1){ans[0]=1;return;}
Exp(d,ans,n0>>1);
Ln(ans,lnans,n0);
for(int i=0;i<n0;i++) lnans[i]=(d[i]-lnans[i]+p)%p;
lnans[0]=(lnans[0]+1)%p;
NTT(lnans,0,n0<<1);NTT(ans,0,n0<<1);
for(int i=0;i<(n0<<1);i++) ans[i]=1LL*ans[i]*lnans[i]%p;
NTT(ans,1,n0<<1);
for(int i=0;i<n0;i++) lnans[i]=0;
for(int i=n0;i<(n0<<1);i++) ans[i]=lnans[i]=0;
}
int lnd[maxN+5];
void Qpow(int d[],int ans[],int n0,int k){
Ln(d,lnd,n0);
for(int i=0;i<n0;i++) lnd[i]=1LL*lnd[i]*k%p;
Exp(lnd,ans,n0);
}
int expd[maxN+5],expnegd[maxN+5];
int main(){
// freopen("testdata.in","r",stdin);
// freopen("fuck.out","w",stdout);
I=qpow(g,(p-1)/4,p);invI=qpow(I,p-2,p);
scanf("%d%d",&N,&opt);
x=1;while(x<(N<<1)) x<<=1,len++;
inv[1]=1;
for(int i=2;i<=x;i++)
inv[i]=1LL*(p-p/i)*inv[p%i]%p;
for(int i=1;i<=len+1;i++){
W[i][0]=1;iW[i][0]=1;
W[i][1]=qpow(g,(p-1)/(1<<i),p),
iW[i][1]=qpow(ig,(p-1)/(1<<i),p);
for(int j=2;j<(1<<(i-1));j++)
W[i][j]=1LL*W[i][j-1]*W[i][1]%p,
iW[i][j]=1LL*iW[i][j-1]*iW[i][1]%p;
}
X=x;
for(int i=0;i<N;i++) scanf("%d",&A[i]),A[i]=1LL*A[i]*I%p;
Exp(A,expd,(X>>1));
Inv(expd,expnegd,(X>>1));
if(opt&1)
for(int i=0;i<N;i++)
printf("%d ",1LL*(expd[i]+expnegd[i])%p*inv[2]%p);
else
for(int i=0;i<N;i++)
printf("%d ",1LL*(expd[i]-expnegd[i]+p)%p*inv[2]%p*invI%p);
}由于公式量太大,本文章已经卡的一匹没法编辑,于是接下来的部分会放到新文章。