关于Phigros自制谱 Algebra AT×SP 16 中的尾杀数学题
NEKO_Daze
·
·
科技·工程
0. 导言
前几天搜自制谱玩的时候发现有一个数学谱大火,点进去一看挺有意思,决定自己做做里面的题。
然而结局是压轴题解了一下午解出来了,几何第四题还不会(哭。所以先把尾杀的题发了。
1.题目观察
1.1 原题
已看过视频的可以跳转到 1.2……
L_1=6,L2=16,L_n=6L_{n-1}-10L_{n-2}\\
\forall k \in N^*,m_1^k+m^k_2=L_k\\
x=\arcsin(\frac{2}{|m_1|+|m_2|})\\
\color{red}a\color{black}=\frac{\sum^\infty_{n=0}\frac{(-1)^n}{(2n+1)!}x^{2n+1}}{\sum^\infty_{n=0}\frac{(-1)^n}{(2n)!}x^{2n}}
S=\{\gcd(88,152),\log_{\sin(\frac{\pi}{4})}2,\tanh 0,\lim_{x\to 0}\frac{\sin(x)}{x}\}\\
p=P(x\in S\mid x \equiv 0(\mod 4))\\
\color{red}b\color{black}=\max\limits_{n}\int^p_n(2x+4) dx
A(3,5),B(5,8),C_1(x_1,y_1),C_2(x_2,y_2)\\
AC_1=BC_1=AC_2=BC_2=\frac{\sqrt{2}}{2}AB\\
f(x)=\ln(x+\sqrt{x^2+1})\\
g(x)=f(f(f(x)+f(-x)))+e^{f(0)}x\\
\color{red}c\color{black}=g(x1+y1)\\
\color{red}d\color{black}=g(x2+y2)
\begin{vmatrix}
a & d \\
c & b
\end{vmatrix} =\space ?
1.2 思路
最终问题是一个矩阵,那么算出前面 a,b,c,d 的值,最后行列式得答案即可(这不是废话吗?
## 2.$a$ 的值
根据初始项 $L_1=6,L2=16$ 和递推关系式 $L_n=6L_{n-1}-10L_{n-2}$ 来推出通项公式。这个递推式是一个二阶线性递推关系其特征方程为 $r^2=6r-10$,解得 $r_1=3+\sqrt{19},r_2=3-\sqrt{19}$。由此推出通项公式为
$$
L_n=A(3+\sqrt{19})^n
+B(3-\sqrt{19})^n$$
其中 $A,B$ 为待定的系数。不过这个通项公式没用,有用的是特征方程的两个根。注意到,题目已说明 $m_1^k+m^k_2=L_k$,是不是和上面的很像?因为 $m_1,m_2$ 就是这两个根。于是我们有 $m_1=3+\sqrt{19},m_2=3-\sqrt{19}$。于是我们代入下面的等式:
$$
x=\arcsin(\frac{2}{|m_1|+|m_2|})=\arcsin(\frac{1}{3})
$$
再观察 $a$ 的等式,不难发现上面是 $\sin(x)$ 的无穷级数展开,下面则是 $\cos(x)$ 的无穷级数展开,因此有
$$
\color{red}a\color{black}=\frac{\sum^\infty_{n=0}\frac{(-1)^n}{(2n+1)!}x^{2n+1}}{\sum^\infty_{n=0}\frac{(-1)^n}{(2n)!}x^{2n}}=\frac{\sin(x)}{\cos(x)}
=\tan(x)=\tan(\arcsin(\frac{1}{3}))=\frac{1}{3}$$
## 3.$b$ 的值
先算出 $S$ 里面的每一个值。
* $88=2^3\times 11,152=2^3\times 19,\gcd(88,152)=2^3=8
-
\sin(\frac{\pi}{4})=\frac{\sqrt{2}}{2},\log_{\sin(\frac{\pi}{4})}2=\log_{\frac{\sqrt{2}}{2}}2=-2
-
-
因此 S=\{8,-2,0,1\}。
最后算积分即可
$$
\color{red}b\color{black}=\max\limits_{n}\int^p_n(2x+4) dx\\
=\max\limits_{n}[x^2+4x]^{\frac{1}{2}}_{n}\\
=\max\limits_{n}(\frac{1}{4}+2)-(n^2+4n)\\
=\max\limits_{n}(\frac{9}{4}-n^2-4n)
$$
易知抛物线 $\frac{9}{4}-n^2-4n$ 的最大值为 $\frac{4ac-b^2}{4a}=\frac{25}{4}$,即为所求。
## 4.$c,d$ 的值
由 $AC_1=BC_1=AC_2=BC_2=\frac{\sqrt{2}}{2}AB$,易知四边形 $AC_1BC_2$ 为正方形。
这里方便演示,画一张图来:
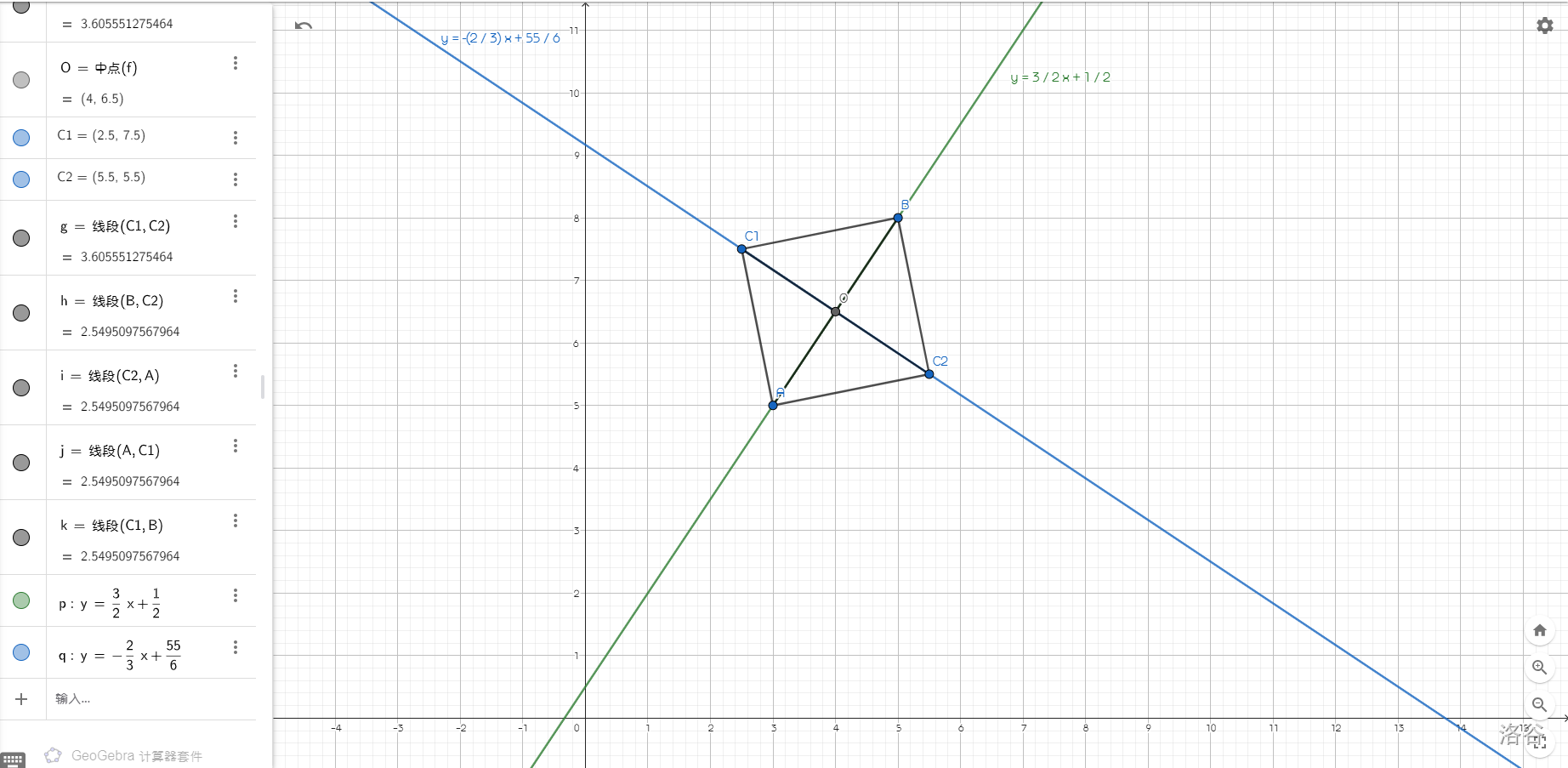
因为已知 $A,B$ 的坐标,我们很容易得知 $AB$ 的解析式为 $y=\frac{3}{2}x+\frac{1}{2}$,又因为 $AB\perp C_1C_2$,所以两条直线的解析式的斜率 $k$ 乘积为 $-1$,因此可设 $C_1C_2:y=-\frac{2}{3}x+b$,又因为 $AB$ 与 $C_1C_2$ 相交于正方形的中心点 $O(4,\frac{13}{2})$(用中点公式可得)。代入解析式解得 $b=\frac{55}{6}$,所以 $C_1C_2:y=-\frac{2}{3}x+\frac{55}{6}$,因此可以将 $C_1,C_2$ 代入,即可用关于 $x_1,x_2$ 的多项式来表示 $y_1,y_2$。然后上两点距离公式:
$$
AC=\frac{\sqrt{2}}{2}AB=\frac{\sqrt{2}}{2} \times \sqrt{(5-3)^2+(8-5)^2}=\frac{\sqrt{2}}{2} \times \sqrt{13}=\frac{\sqrt{26}}{2}\\
AC^2=\frac{13}{2}\\
AC^2=(x-3)^2+(-\frac{2}{3}x+\frac{55}{6}-5)^2=\frac{13}{2}
$$
容易看出这是一个一元二次方程,化简得
$$
\frac{13}{9}x^2-\frac{104}{9}x+\frac{715}{36}=0
$$
解得 $x_1=\frac{5}{2},x_2=\frac{11}{2}$。然后代入原解析式得出 $y_1=\frac{15}{5},y_2=\frac{11}{2}$。
到这里就已经完成一半了,接下来我们只需要算出 $g(\frac{5}{2}+\frac{15}{5})=g(10),g(\frac{11}{2}+\frac{11}{2})=g(11)$ 的值即可。
注意到(真的可以注意到,随便代入一个数即可),$f(x)+f(-x)=0$,而且又有 $f(0)=\ln(1)=0$,所以有
$$
g(x)=f(f(f(x)+f(-x)))+e^{f(0)}x\\
=f(f(0))+e^0x\\
=f(0)+1\times x\\
=0+x=x
$$
因此 $c=g(10)=10,d=g(11)=11$。
## 5.最终の矩阵
万事俱备,只欠矩阵。
将 $a=\frac{1}{3},b=\frac{25}{4},c=10,d=11$ 代入矩阵行列式得
$$
\begin{vmatrix}
a & d \\
c & b
\end{vmatrix} =ab-cd=\frac{25}{12}-110=-\frac{1295}{12}.
$$
**综上,$\begin{vmatrix}
a & d \\
c & b
\end{vmatrix} =-\frac{1295}{12}$。**