关于欧拉圆

· · 个人记录

说明

如图，A,B,C为任意三角形定点。

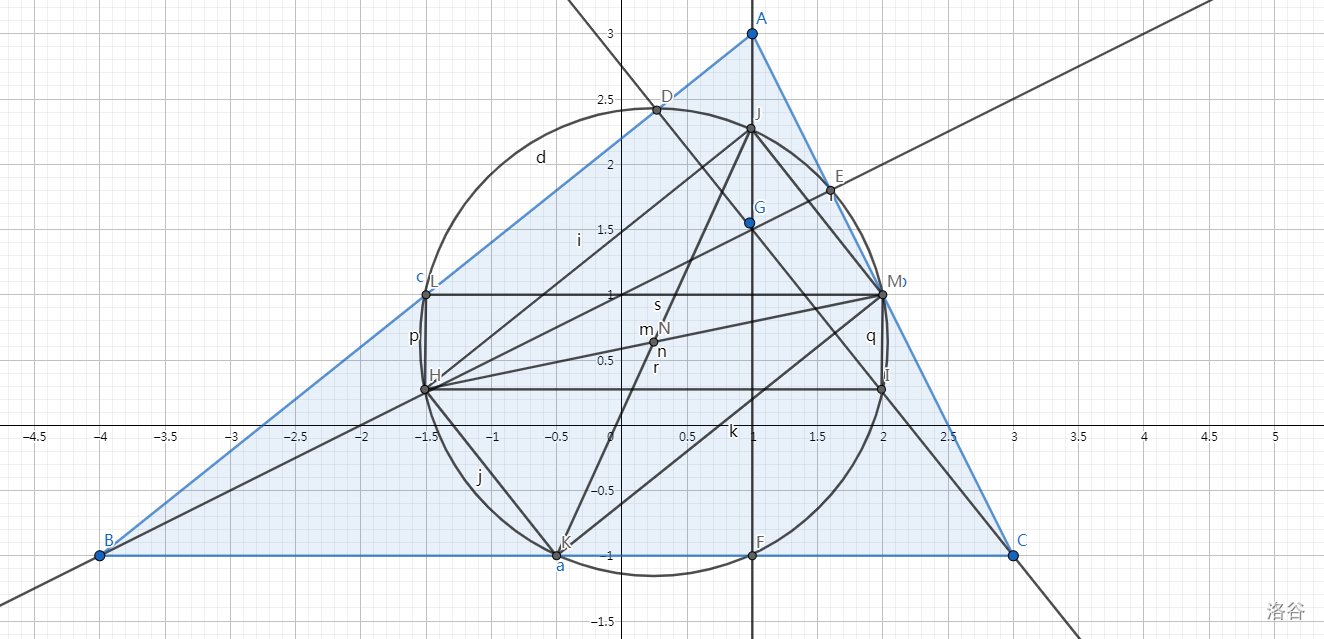
$AF,BE,CD$相交于点$G$。 $L,M,K$分别为$AB,AC,BC$的中点。 $H,I,J$分别为$BG,CG,AG$的中点。 则$L,D,J,E,M,I,F,K,H$九点共圆。 ## 证明 ![](https://cdn.luogu.com.cn/upload/image_hosting/x3vkzkzl.png?x-oss-process=image/resize,m_lfit,h_1500,w_2000) 连接$KM,JK,MH,JH,HK,JM,LM,LH,IM,LM,HI$。 $\because MK//JH//AB$且$MK=JH=AB/2$且$KH//CG,CG \perp AB$(中位线) $\therefore$ 四边形$KMJH$为矩形 $\therefore$ $K，M，J，H$四点共圆，且$MH$和$JK$的交点$N$为圆心 $\therefore$ 四边形$LHIM$为矩形 $\therefore$ $K,I,M,J,L,H$六点共圆 $\therefore$ $LI,HM.JK$为此圆的直径 又$\because$ $\angle JFK=\angle HEM =\angle LDI=90^o